考慮裁切線的張拉膜結構水平風荷載響應分析

武紅周

(中鐵七局集團海外公司，河南 鄭州 450016)

0 引言

張拉膜結構是由膜面、拉索以及支撐結構等構成的穩定結構體系。膜和索只受拉，施工中通過對鋼索和膜面施加預拉應力，使其具有足夠的剛度以承擔外部荷載，支撐結構則作為主要的受壓構件，承受索具傳遞下來的荷載。

膜結構體型復雜，自重較小，屬風敏感結構，在風荷載作用下，結構容易出現強機構性特征，所以對膜結構的動力特性研究就顯得非常重要[1-3]。近年來，人們對體型簡單的膜結構研究已經較為成熟，尤其在對膜結構裁剪分析和風荷載分析方面，但是對帶有裁切線的膜結構抗風荷載性能研究相對較少。本文對無裁切線和有裁切線兩種情況進行數值模擬，并對比數值模擬結果，探討裁切線對風荷載作用下膜結構的承載性能影響[4]。

1 分析模型

1.1 風荷載靜力分析

膜結構在荷載作用下的變形屬于大變形范疇，分析中要考慮幾何非線性和材料非線性問題，但在膜結構實際應用中，膜面應力的變化范圍卻很有限，一般處于材料彈性階段，為了簡化荷載分析問題，一般認為膜面應力應變為彈性關系。對膜結構進行靜力荷載分析時，風荷載一般考慮為水平向荷載，通過轉化為等效節點荷載進行加載[5]。

1.2 風荷載動力分析

風荷載動力分析的本質是將自然風加載到結構上，最終得到結構的時程響應。通過圖1風速時程曲線可以發現，任一點的瞬時風都可以分解成兩部分：一種是10 min以上的長期部分，即平均風，也稱穩定風；另一種是周期只有幾秒且均值為零的部分，稱為脈動風[6]。

(1)

風壓可分為平均風壓和脈動風壓：

(2)

平均風一般遠離結構的自振周期，對結構的作用屬于靜力特性。脈動風與結構的自振周期較為接近，其作用屬于動力特性[7-8]。

脈動風的風速和風向都是隨著時間和空間變化的，具有明顯的隨機性，但通過對大量的實測記錄樣本時程曲線分析，發現脈動風速本身可以用具有零均值的高斯平穩隨機過程來模擬，且具有明顯的各態歷經性。Davenport[9]提出不隨高度變化的水平脈動風速功率譜Sv(ω)，作為目前工程中廣泛使用的順風向水平脈動風速譜，也是我國規范所采用的風速譜[10-12]。

(3)

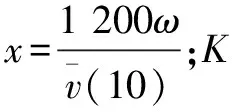
我國荷載規范規定平均風速沿高度變化規律用指數函數表示：

(4)

其中，α為地面粗糙度系數；Z為距離地面高度。

我國建筑結構荷載規范[13]規定計算靜力風壓的公式為：

ωk=βzμzμsω0

(5)

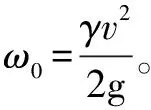
根據分布規律，將表面劃分為若干區域，使每個區域內的風壓分布系數Cpi值盡可能接近，然后對區域內各個測點的風壓分布系數Cpi與其所屬面積Ai的乘積取加權平均值，得值即為區域風載體型系數[14-16]。

(6)

2 實例分析

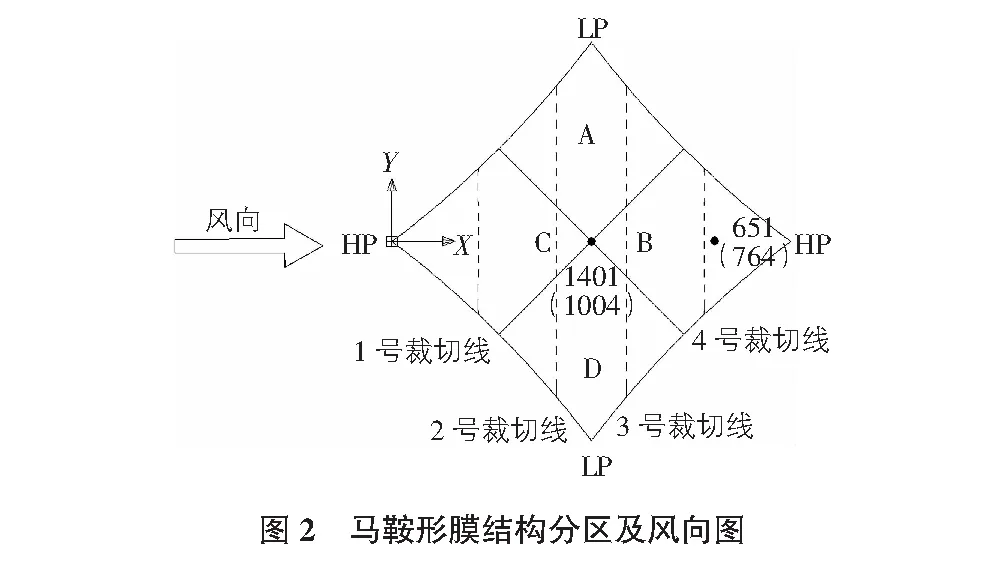
該馬鞍形張拉膜結構，結構的4個角點是固定的，對角線長度為l=5 m，高度h=2.5 m，下部開敞，最低點距地面2.5 m。膜面初始預應力2 kN/m，張拉剛度255 kN/m，材料自重：膜材1 050 kg/m3, 索7 850 kg/m3，裁切線按圖2布置。

2.1 靜力荷載分析

風荷載靜力分析：風荷載0.35 kN/m2。

靜力荷載作用下的無裁切線膜結構、帶裁切線膜結構見圖3，圖4。

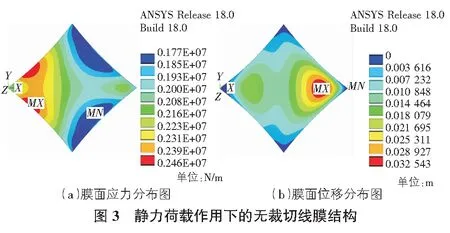
通過對比圖3和圖4可以發現：

1)裁切線會對靜荷載作用下的膜面應力分布以及膜面位移產生影響，但膜面應力和位移較大的區域位置大致相同。

2)當裁切線存在時，帶裁切線的膜面應力最大值為3.17 kN/m，比無裁切線的膜面應力最大值2.46 kN/m大0.71 kN/m，超過約30%，且較大應力都出現在1號裁切線與邊索交接區域，帶有裁切線的膜面應力最大值區域出現在4號裁切線中部。

3)帶有裁切線的膜面位移最大值為60 mm，比無裁切線的位移最大值大28 mm，兩者大位移區域位置大致相同，但帶有裁切線的膜面大位移區面積小于無裁切線大位移區域面積。

2.2 動力荷載分析

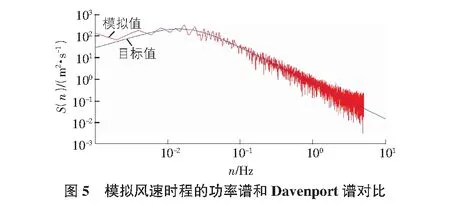
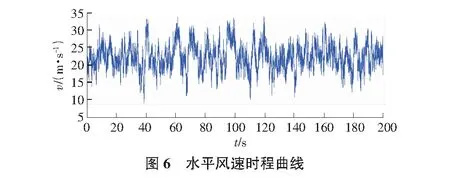
風荷載動力分析：水平風由高點吹過，0°風向角，膜結構體型系數分區采用膜結構技術規程[17]的劃分樣式，見圖2。風速譜選用Davenport譜(見圖5)，地面粗糙度為B類，平均風速為22 m/s，采用MATLAB進行風速模擬[18-20]，取其中40 s的風速時程曲線進行模擬(見圖6)，取膜面中心點和4號裁切線中間附近位置點的z向位移時程曲線。計算過程中假設滿足下列條件：

1)膜面各點風速時程曲線相同。2)膜面只承受水平風荷載[21]，不考慮垂直和橫向脈動風影響。

動力風荷載作用下，膜面選取節點的位移響應和應力響應見圖7，圖8。

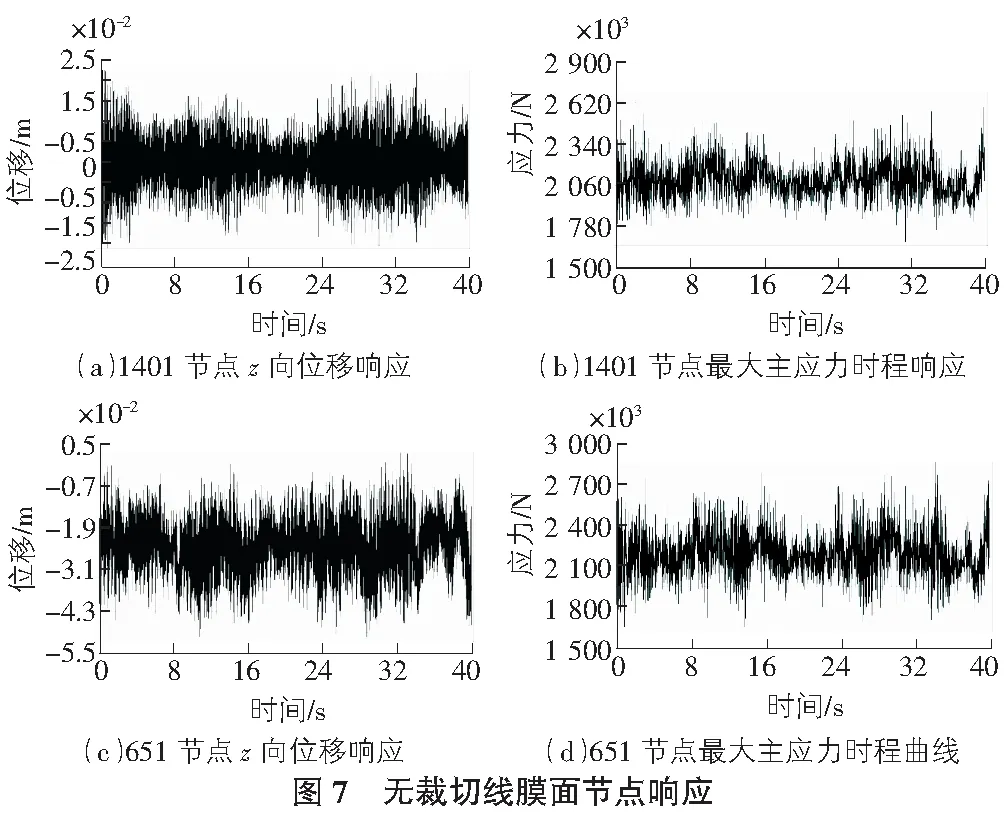
通過圖7,圖8對比可知：1)動力風荷載作用下，帶有裁切線的膜面中心點位移最大值為30 mm，較無裁切線膜面中心點位移最大值25 mm，位移增大20%，裁切線中間附近點位移最大值大致相等；2)帶有裁切線的膜面中心點位移幅值為55 mm，較無裁切線膜面中心點位移幅值45 mm，增大22%，可見帶有裁切線的膜結構中心處響應幅度更明顯；3)有無裁切線的膜面中心點處應力均在2.05 kN/m波動，有裁切線的膜面中心點應力區間1.72 kN/m～2.45 kN/m，相比較無裁切線的中心點應力區間1.65 kN/m～2.7 kN/m，應力變化范圍小，但位移變化區間要更大；4)兩種膜面裁切線中間附近點處的應力和位移均大致相等。

為更直觀全面了解兩種不同膜面，在水平風荷載作用下，整個膜面的位移和應力分布情況，現取兩種膜面在第40秒的位移和應力分布圖(見圖9)。張拉膜結構最大應力對比見表1。

表1 張拉膜結構最大應力對比

通過圖9并結合表1可知：

1)在水平風動力荷載作用下，帶有裁切線的膜結構位移最大值達到51 mm，大于無裁切線的43 mm約20%，可見，裁切線對膜面風振效應明顯。

2)將風載考慮為動載時，有裁切線膜面的最大主應力變化較小，且應力分布狀況與無裁切線膜面大致相同，但高應力區面積較無裁切線膜面明顯增加，低應力區面積明顯低于無裁切線膜面。

3)膜結構帶有裁切線以后，在水平風動力荷載作用下，膜面應力差為2.15 kN/m，遠大于無裁切線膜面的應力差1.72 kN/m，可見，裁切線會導致膜面應力分布不均勻性增加。

4)通過比較膜面應力分布會發現，帶有裁切線的膜結構，承受荷載時的最大主應力分布面積大于無裁切線膜面，且最小主應力大都分布于膜面連接處及兩側帶狀區域，小區域內應力值變化較大，膜面出現局部褶皺甚至破壞的概率增加。

3 結語

裁剪和抗風設計是膜結構設計中必不可少的階段，裁切線不僅關系到膜結構施工后的膜面形狀及應力分布，而且對膜結構使用過程中抵抗風荷載能力產生一定影響。本文通過MATLAB編制相應的程序模擬脈動風速譜，忽略膜結構的幾何非線性和材料非線性影響，假定材料應力應變為彈性關系，完成膜面裁剪前后的風荷載靜力分析以及時程響應分析，得出裁切線會降低張拉膜結構在風荷載作用下的承載能力。

本文主要針對水平風向0°角的脈動風進行模擬計算，未來還需對其他角度水平風、橫向風、垂直風以及流固耦合綜合研究，以更真實模擬自然風下的張拉膜結構承載特性。