地震作用下柱承式筒倉動態側壓力計算方法研究

陳佳，丁永剛，2，許啟鏗，2，劉強，索煥

（1.河南工業大學土木工程學院，河南 鄭州 450001；2.河南省糧油倉儲建筑與安全重點實驗室，河南 鄭州 450001）

引言

鋼筋混凝土柱承式筒倉是應用于糧食、煤炭、建材等倉儲物流行業的通用性構筑物。在地震作用下，筒倉除了受到結構本身的慣性力外，倉壁上還會產生貯料的動態側壓力，引起倉壁的側向變形和較大的動態超壓問題［1］。在地震頻發區，已經成為筒倉結構破壞的主要原因之一［2］。國內外相關學者對筒倉結構的動態側壓力問題進行了相應研究，Chowdhury等［3－4］將貯料看作一種集中質量施加到倉壁上，推導了矩形儲煤倉結構倉壁動態側壓力計算方法，部分學者通過振動臺試驗研究證明該方法和歐洲規范規定的計算方法過于保守［5－7］。Silvestri等［8－10］基于貯料散體和倉壁相互作用及顆粒剪切效應提出了新的動態側壓力計算方法。但通過鋼筒倉振動臺試驗［11］研究驗證，發現該方法僅適用于淺圓倉（高徑比大于0.4且小于1.0），尚不適用于筒倉［12］（高徑比大于或等于1.5）。施衛星等［12］采用非線性地震反應分析方法，在筒承式單倉振動臺試驗的基礎上建立了煤倉動態側壓力計算公式。在此基礎上，周長東等［13］考慮了貯料高度、地震動強度、貯料內摩擦角和貯料與倉壁之間的摩擦系數對側壓力的影響，通過數值分析確定了貯料側壓力修正系數，進一步推導了筒倉和貯料相關作用的貯料側壓力修正公式。劉海林［14］嘗試從離散元角度分析了不同高徑比情況下的筒倉卸料壓力增加機理，提出了適用于圓形淺倉且考慮倉壁和貯料彈性的側壓力計算方法。

由于缺乏筒倉貯料動態側壓力計算方法，現行規范并未涉及筒倉結構地震作用引起的動態側壓力，而是僅考慮了筒倉卸料為主要因素的超壓系數進行結構設計［15］。顯然，隨著倉儲結構抗震設防和防災減災能力需求不斷提高，急需探索研究地震作用下筒倉結構貯料動態側壓力的計算理論和方法，以進一步提高筒倉結構安全和抗震韌性。

丁永剛等［16－19］進行了倉儲結構地震響應研究，通過振動臺試驗獲得了柱承式筒倉、排倉以及群倉結構在地震作用下貯料動態側壓力的分布規律和超壓系數。為此，文中在現有研究基礎上，以柱承式筒倉結構為研究對象，通過理論分析探究適用于筒倉地震作用下的貯料動態側壓力計算方法。在此基礎上，基于柱承式筒倉結構的數值算例與振動臺試驗數據，驗證了該方法的有效性，并分析其在不同加速度峰值下的倉壁動態側壓力分布規律，為完善筒倉結構抗震設計理論和方法提供參考。

1 筒倉倉壁分析模型

1.1 基本假設

基于Airy靜壓力理論［20］，確定帶有失效楔塊的柱承式筒倉計算簡圖，如圖1所示。針對高徑比較小的淺圓倉圖1（a），倉內貯料形成了失效楔塊ABC后，倉壁上產生靜壓力，假設失效楔塊形成的角度為θ。根據失效楔塊ABC的靜力平衡條件可知，作用在倉壁上的水平力P可以表示為：

根據Airy理論［20］，若P取最大值，則應滿足，進而可得：

式中：P為倉壁水平側壓力；W為失效楔塊的重力；θ為失效楔塊形成的角度；μ為倉內貯料顆粒間摩擦系數；μ′為倉內貯料與倉壁間摩擦系數。

為確定基于倉壁壁板振動分析的計算模型，結合上述分析，有下列基本假設成立：

（1）由式（2）可知，筒倉內已經形成楔塊的貯料處于極限失效狀態，本身沒有剛度，在地震作用下，可以認為失效楔塊ABC被懸掛在倉壁上，只提供慣性作用。

（2）與失效楔塊相比，柱承式筒倉倉壁較薄，假設倉壁只對筒倉結構提供剛度貢獻。

（3）考慮到筒倉頂部通常設有倉上設備，將倉壁視為四邊為固定約束的壁板。

對于圖1（b）所示的筒倉結構，倉壁上產生的靜壓力是由于倉內貯料形成了失效楔塊ABCD后引起的。對于地震作用下筒倉動態側壓力問題可以等效為支撐失效楔塊ABCD的四邊固定壁板的振動問題。同樣，可以得到：

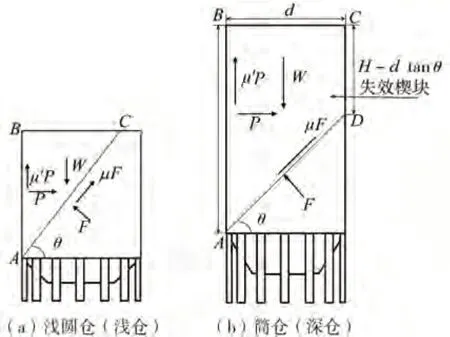
圖1 帶有失效楔塊的柱承式筒倉簡圖Fig.1 Structure diagram of a column-supported silo with failure wedge mass content

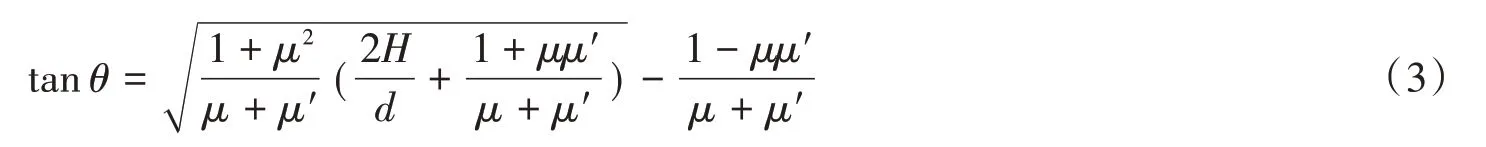
式中：H為倉壁高度；d為筒倉直徑；θ為失效楔塊形成的角度；μ為倉內貯料顆粒間的摩擦系數；μ′為倉內貯料與倉壁間摩擦系數。

筒倉中失效楔塊ABCD由三角形和矩形組成，其慣性質量對筒倉結構在地震作用下的動態側壓力響應有貢獻。為方便公式推導，將失效楔塊ABCD轉化為具有相同高度（H）但直徑不同的面積相等的等效三角形。根據面積關系S′Δ=SABCD和tanθ′=H/d′Δ，可得：

由式（5）可以看出，對于筒倉結構倉壁來說，失效楔塊形成的夾角θ′受高徑比影響。

1.2 計算模型

為方便計算，針對柱承式筒倉倉壁，取簡化后的壁板模型進行分析。該簡化模型可以實現將倉壁動態側壓力問題簡化為支撐三角形失效楔塊的四邊固定壁板的振動問題。取筒倉倉壁部分弧形壁面進行分析，展開得到高寬為H×b的壁板。地震作用下倉壁壁板振動分析模型如圖2所示。

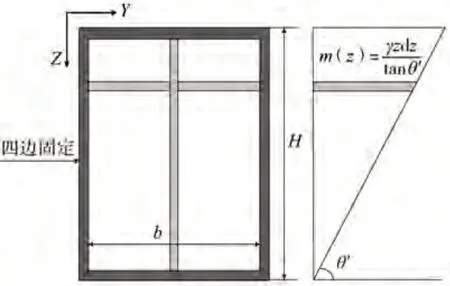
圖2 地震作用下支撐失效楔塊的深倉壁壁板（四邊固定）Fig.2 Slender silo wall with failure wedge mass content under earthquakes（four edges fixed）

由振動的模態疊加原理［21］可知，地震作用下，倉壁的變形按照振型函數展開為：

式中：qi(t)為廣義坐標；?i(z,y)為倉壁壁板在地震作用下的振型函數。

筒倉結構的動能可以表示為：

將式（6）代入式（7），得到：

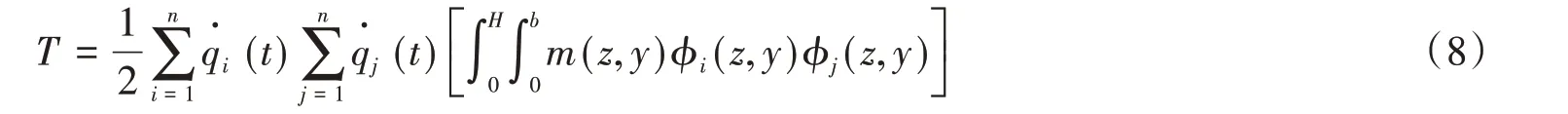
式（8）第3項為質量系數表達形式，即：

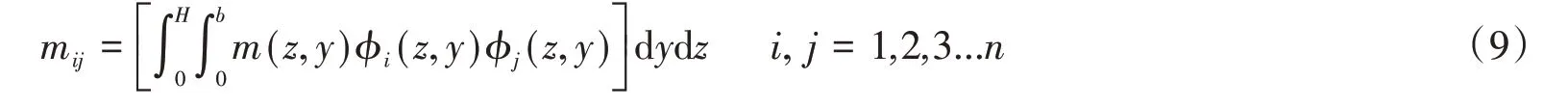
對于倉壁壁板來說，其彎曲變形能為：

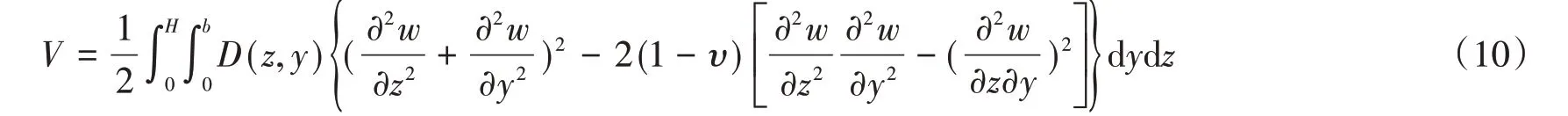
根據拉格朗日方程，可以證明式（10）關于qj(t)對于各向同性的倉壁壁板的剛度系數可以表示為：

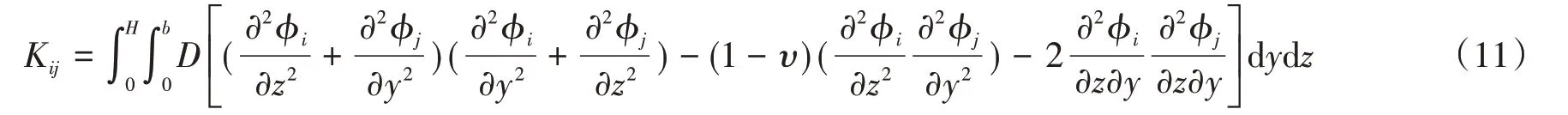
式中：D為薄板的彎曲剛度，D=，其中，E為材料彈性模量；δ為倉壁厚度；υ為材料泊松比。?i,?j為倉壁壁板在在地震作用下z和y方向的振型函數。

選取倉壁壁板y和z方向上的微條單元進行分析，如圖3所示。根據假設條件（3），微條被簡化為兩端固定的梁單元。通過求解兩端固定梁彎曲振動微分方程，可得到振型函數，即：

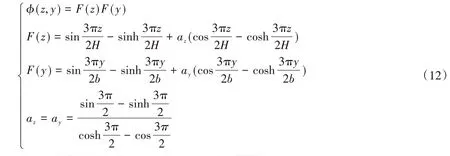
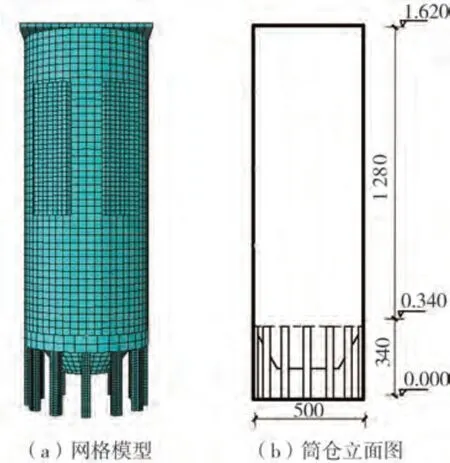
圖3 有限元模型及網格劃分（單位：mm）Fig.3 FEM model and grid division（Unit：mm）

2 倉壁動態側壓力計算方法

2.1 等效質量和剛度系數

深倉倉壁的質量系數和剛度系數是倉壁動態側壓力計算公式推導的基礎物理量。為了方便后期推導，首先確定支撐失效楔塊的倉壁（簡化計算模型）的質量和剛度系數。通過對微條單元取基振型進行分析，?i(z,y)=?j(z,y)，將其代入式（9），得到：

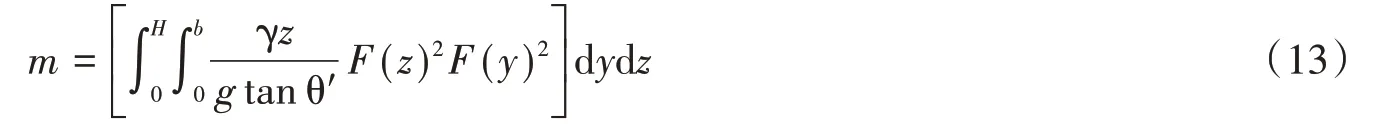
將式（12）代入式（13），并令z=Hξ,y=bη即可得到：

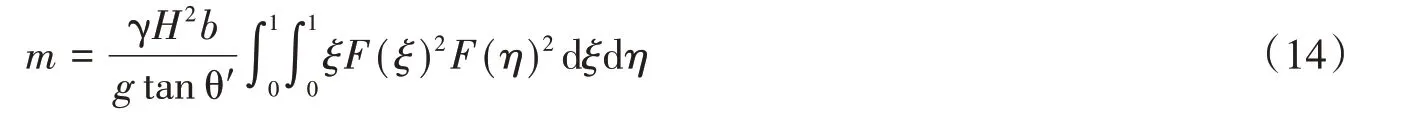
同樣，將式（12）代入式（11）中可得到，

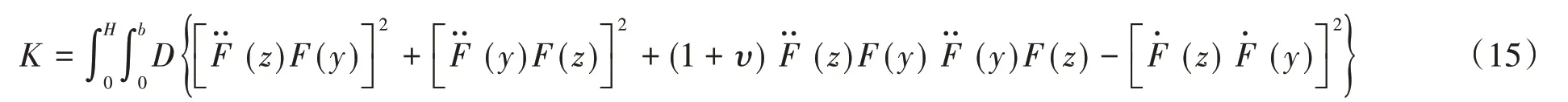
為了方便計算，將振型函數F(z)和F(y)轉化為自變量在（0～1）范圍內的函數f(ξ)和f(η)。令z=Hξ,y=bη，則可得到：

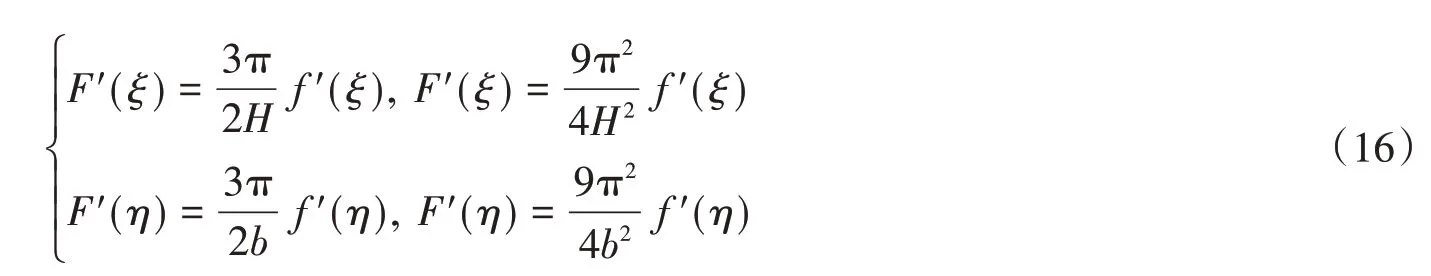
將式（16）代入式（15），得剛度系數為

式中：C1～C5可采用辛普森積分法求解；γ為儲料重度；H為振動模型壁板高度；b為振動模型壁板寬度；g為重力加速度；θ為失效楔塊形成的角度；D為倉壁壁板的抗彎剛度。

2.2 倉壁動態側壓力

基于彈性力學理論，將地震作用下筒倉倉壁的動態側壓力問題簡化為支撐失效質量塊的貯料壁板的振動問題。因此，根據薄板彎曲的基本微分方程求解筒倉倉壁在地震作用下的動態側壓力，即：

式中：D為薄板的彎曲剛度；w(z,y,t)為地震作用下倉壁的位移函數

式中：Sa為柱頂加速度反應譜；ω為固有頻率；ki為振型參與系數，且由式（14）計算可取，ki=，可采用辛普森積分法求解。

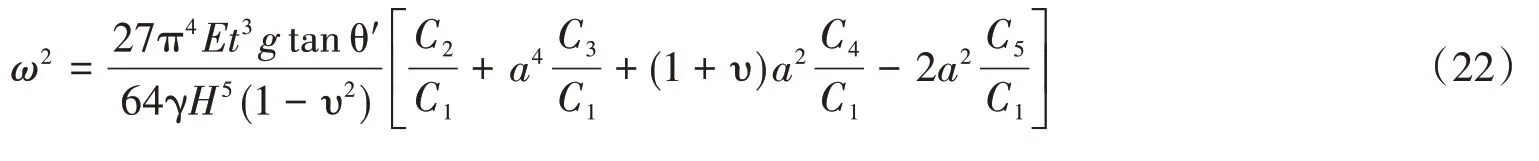
式中：a為倉壁壁板的高徑比（H/b）；C1～C5可采用辛普森積分法求解。

令f(a)=，則f(a)作為已知量代入式（22），結合式（16）和式（21），得到：

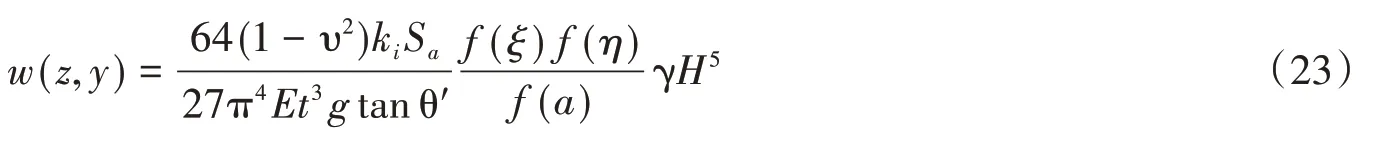
將式（23）代入式（20），最終得到倉壁上產生的動態側壓力：

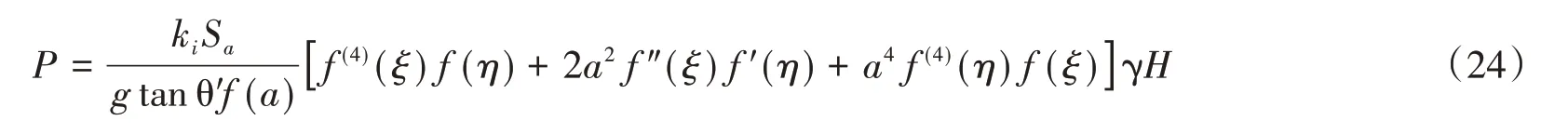
由式（24）可以看出，動態側壓力P受筒倉結構高徑比、倉內貯料顆粒間、貯料與倉壁間摩擦系數、柱頂加速度反應譜、倉壁振型函數的影響。其中，柱頂加速度反應譜可以通過振動臺試驗實測獲得。基于四邊固定壁板振動模型的動態側壓力隨倉壁振型函數選取的不同而變化，是基本形狀函數及其及其導數、柱頂加速度反應譜和高徑比的函數。該公式反映了高徑比大于或等于1.5條件下柱承式筒倉倉壁振動對筒倉結構的動態側壓力貢獻大小。該公式為計算柱承式筒倉貯料動態側壓力提供了理論參考。

3 數值算例與對比驗證

3.1 數值算例

選取幾何尺寸如圖3（b）所示的深倉條件下的柱承式筒倉進行有限元ABAQUS數值分析。筒倉高徑比為2.56，筒倉壁厚取10 mm。有限元模型材料與丁永剛等［17］開展的振動臺試驗模型保持一致。結構和貯料均采用實體單元。貯料與倉壁之間考慮接觸關系，并設置切向接觸為摩擦，法向接觸為硬接觸，貯料與倉壁之間摩擦系數取0.45。倉壁約束條件結合筒倉實際支撐條件和我國規范確定為：支承柱頂部與倉壁底部接觸位置為綁定關系；支承柱底部為固定約束；考慮到倉上設備的存在，設置倉壁頂部為綁定。貯料采用D－P本構模型。三維有限元模型網格劃分如圖3（a）所示。文中根據丁永剛等［17］開展的振動臺試驗所確定的貯料材料參數取值如表1所示。

表1 貯料材料參數Table 1 Parameters of storage materials

3.2 對比驗證

由式（24）可以看出，地震作用下的動態側壓力受筒倉結構高徑比、倉內貯料顆粒間、貯料與倉壁間摩擦系數、柱頂加速度反應譜、倉壁振型函數的影響。對于以上4個方面的影響因素均應采用試驗驗證其影響規律。限于篇幅，對于某一個確定的筒倉（深倉）結構而言，地震作用對其動態側壓力分布規律起主導作用。因此，文中進行了不同地震加速度峰值下筒倉側壓力理論計算值、有限元值和試驗結果對比分析，用以驗證文中提出的基于筒倉壁板分析的動態側壓力計算方法的正確性。

依據文中建立的有限元數值分析模型，在筒倉結構的x方向分別輸入不同加速度峰值的El Centro波、唐山波和人工波，加速度峰值分別為0.062 5、0.125、0.25 g。計算時取10 s地震波記錄。考慮筒倉結構處于線彈性變形范圍，得到柱承式筒倉結構和倉壁側壓力計算結果。限于篇幅，圖4和圖5所示為El Centro波作用下的倉壁側壓力和筒倉結構等效應力云圖。

圖4 筒倉壁板側壓力Fig.4 Lateral pressure of slender silo wallboard

圖5 筒倉結構等效應力Fig.5 Equivalent stress of slender silo

由圖4和圖5可以直觀地觀察到，考慮筒倉結構處于線彈性范圍，柱承式筒倉倉壁在地震加速度峰值分別為0.062 5、0.125、0.25 g時，其倉壁壁板的應力峰值均出現在壁板底部。這是由于有限元數值分析提取的筒倉壁板側壓力結果是基于靜態側壓力的疊加值。圖4筒倉壁板側壓力云圖趨勢表現為地震作用下倉壁受到的動態側壓力與靜態側壓力的疊加。鑒于此，建議在柱承式筒倉結構的柱頂和環梁位置采取加強措施，以保證結構的整體安全性。

在團隊前期研究成果中，丁永剛等［17］開展了與文中數值模型和相關材料參數一致的單向地震作用下柱承式筒倉振動臺試驗，獲得的動態側壓力分布規律沿筒倉倉壁深度方向呈現“中間大，兩端小”。試驗所測側壓力為動態側壓力凈值，不包括靜態側壓力。為了更清晰的呈現對比分析結果，采用文中提出的倉壁動態側壓力計算方法得到的柱承式筒倉倉壁壁板側壓力理論值。結合有限元計算結果，提取了壁板動態側壓力峰值。最終將文中得到的理論值、有限元計算結果和丁永剛等［17］開展的柱承式筒倉模型振動臺試驗結果進行對比分析，分析結果如表2所示。

由表2數據可以得到，在El Centro波的地震作用下，筒倉結構的壁板應力隨著地震加速度峰值的增加而不斷增大，且理論值、試驗值和有限元值吻合良好，相對誤差均小于4.0%，這表明文中提出的柱承式筒倉動態側壓力計算方法合理可行。該方法可以為筒倉結構在地震作用下的動態側壓力計算提供理論參考。

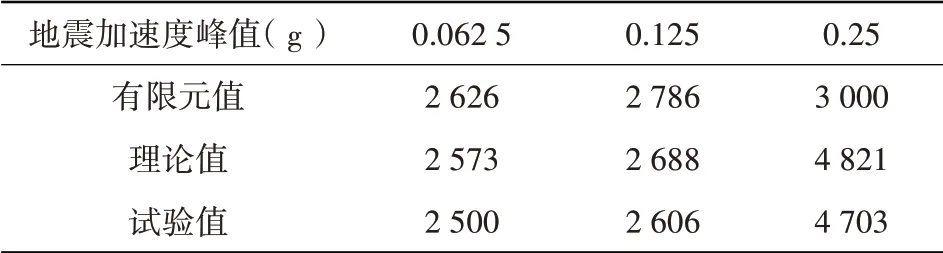
表2 不同地震加速度峰值下筒倉壁板側壓力峰值Table 2 Peak lateral pressure of silo wallboard under different seismic acceleration peaks Pa

為了更直觀地觀察動態側壓力沿筒倉深度方向的變化規律，提取了柱承式筒倉結構在El Centro波、唐山波和人工波作用下加速度峰值分別為0.062 5、0.125、0.25 g時倉壁不同位置處（0.3、0.6、0.9、1.2 m）側壓力計算結果，繪制側壓力隨深度變化圖，如圖6所示。

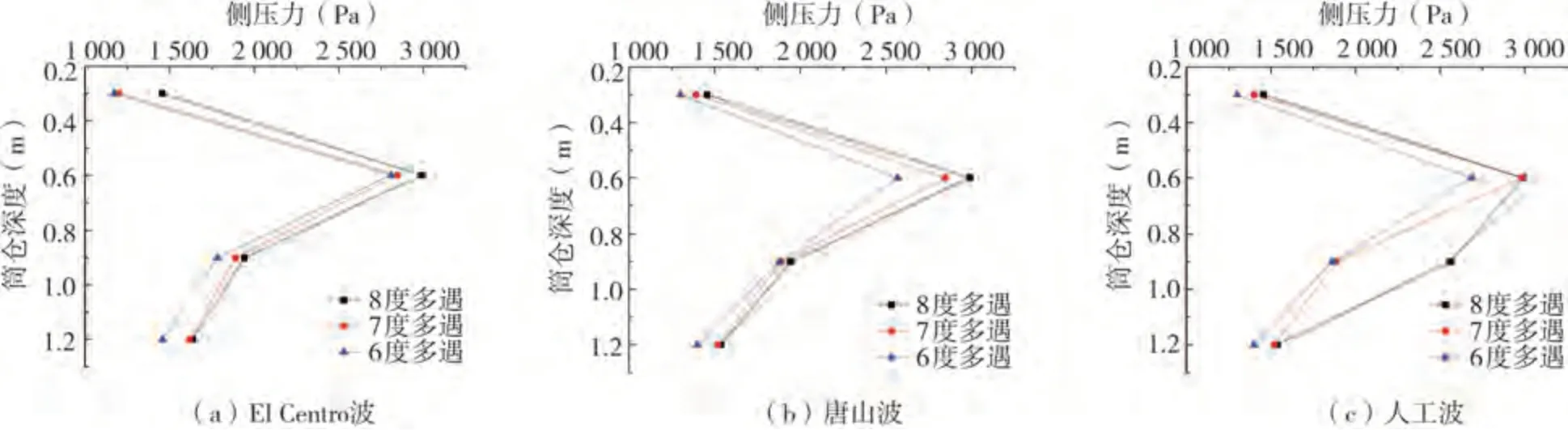
圖6 3種地震波作用下不同地震加速度峰值的倉壁側壓力沿深度分布Fig.6 Lateral pressure along the depth of slender silo wall under different seismic acceleration peaks with the action of 3 different seismic records

由圖6可以得到，考慮筒倉結構處于線彈性范圍，柱承式筒倉倉壁在地震加速度峰值分別為0.062 5、0.125、0.25 g時，在一定深度范圍內倉壁壁板側壓力變化規律是隨深度增加而增加。但超過一定范圍后，隨深度的增加而減小，但呈非線性減小趨勢，表現為動態側壓力響應規律沿筒倉倉壁深度方向呈現“鐘形分布”（中間大，兩端小）。然而，對于不同地震波作用下柱承式筒倉倉壁壁板側壓力變化規律整體趨勢一致，但人工波作用下不同地震加速度峰值的倉壁壁板側壓力響應較為敏感。這是由于貯料特性、貯料與倉壁摩擦特性的影響，使筒倉結構受到的地震反應隨不同地震波類型和加速度峰值的變化有所差異。

4 結論

通過將地震作用下筒倉動態側壓力問題簡化為支撐失效質量塊的貯料壁板振動問題，提出了基于四邊固定彈性壁板振動模型的柱承式筒倉動態側壓力計算方法，并建立有限元數值分析模型，進行不同加速度峰值情況下的結果驗證與對比分析。主要結論如下：

（1）提出的柱承式筒倉動態側壓力計算方法能夠合理地反映地震作用下倉壁側壓力分布規律，計算精度較高，為筒倉結構地震作用下的動態側壓力計算提供了理論依據。

（2）柱承式筒倉結構的動態側壓力隨地震加速度峰值的增加而增大。且沿筒倉深度方向呈現“鐘形分布”趨勢（中間大，兩端小），其峰值向倉壁中下部位置集中。動態側壓力是筒倉結構設計不可忽視的一個重要作用力。

（3）針對設防烈度較高地區，建議在柱承式筒倉結構柱頂和環梁部位采取加強措施，以保證筒倉結構的整體安全性。