SV波垂直入射下成層半空間地震動輸入模型比較

渠艷齡，朱柏潔

（1.中國地震局工程力學研究所地震工程與工程振動重點實驗室，黑龍江 哈爾濱 150080；2.地震災害防治應急管理部重點實驗室，黑龍江 哈爾濱 150080）

引言

在土－結構動力相互作用分析中常采用人工邊界模擬幾何無限土域的動力特性。此時，遠場地震荷載由于無限土域的簡化而無法直接獲取。考慮到地震波通過人工邊界進入近場，可根據地震波傳播規律，將遠場地震動轉化人工邊界處的等效地震力。一種轉化方法是考慮地震波從近場下臥層介質向上傳播，到達地表后反射至下臥層，并向無窮遠處傳播。此時，等效地震力施加在近場側邊界處和底部（下臥層）。均質介質中的自由場運動可通過波動理論方便求解［1］。然而，對于復雜場地條件下側邊界處自由場運動往往不易求得［2］。研究表明，當側邊界距離場地中心約為10倍場地深度時，側邊界處的地震力對自由場運動影響較小［3－4］。因此，另一個地震動輸入的方法是僅考慮近場底部地震動輸入，而忽略側邊界處的自由場運動效應［5－6］。目前，關于地震動輸入模型的成果很多，但是側邊界處地震力對自由場運動的影響仍有待進一步研究［7］。

Li等［8］用波動法求得側向人工邊界處等效地震力，并通過數值計算研究了該地震力對土－結構體系的影響。研究表明，僅考慮下臥層地震荷載得到的自由場運動數值結果與理論解偏差很大。Zhang等［5］和Zhao等［9－10］采用一維控制方程描述了二維自由場運動，計算結果證實當成層介質水平向尺寸足夠大時，側邊界處自由場允許效應可以忽略。杜修力等［7］結合理論分析和數值模擬方法，分析了下臥剛性基巖條件下土－結構體系地震反應。研究指出，在通常的工程經驗尺度內忽略側邊界處自由場效應影響無法得到正確的計算結果。然而，上述研究采用的人工邊界均不能完全吸收外行波，因此相應的計算結果存在一定誤差。

比例邊界有限元法［11］結合了有限元和無限元的優點，在模擬裂縫拓展［12］、網格剖分［13］以及地震波傳播［14］等方面有顯著的優勢。比例邊界有限元法是一種半解析的計算方法，它可在有限元精度內準確模擬矢量和標量外行波的傳播特性。文中研究了平面SV波垂直入射下自由場場地響應，利用比例邊界有限元法準確模擬了幾何無限介質的動力特性，分別采用僅近場底部輸入和底部、側邊界同時輸入的地震動施加方式，通過理論分析和數值模擬比較了兩種輸入方式的異同，研究了側邊界處地震荷載對自由場響應的影響，為求解成層半空間介質地震波傳播提供理論依據和數值求解技術。

1 地震荷載輸入方式

成層半空間內地震波的波動問題如圖1所示。二維近場的寬度為2d，深度為h。平面地震波從無限遠處以入射角為θ向右上方入射。當平面波抵達近場的左下角（－d，－h）時設為時間起點t=0。

無阻尼自由場運動的時域控制方程為：

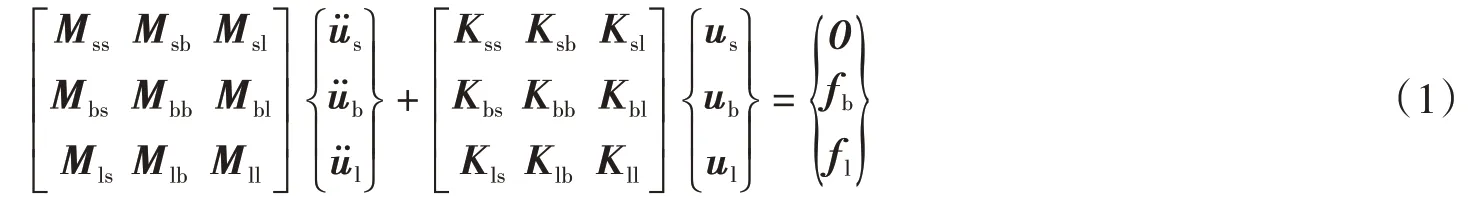
式中：M，K分別為近場的質量矩陣和剛度矩陣；u為位移矩陣；下標b，l，s分別表示在近場底部、側邊以及近場內其余各點處的自由度，如圖2所示。由于地震波在傳播過程中穿過近場與遠場的交界面b和l，因此b和l邊界處均有等效地震力f。為了方便分析，本節理論在頻域內展開。控制方程（1）的頻域表達式為：

式中：S代表頻域內自由場動力剛度；U和F分別為頻域內位移幅值和等效地震力幅值。式（2）考慮了近場底部b和側邊界l處的等效地震力輸入。這一輸入方式定義為模型BL。如果僅輸入側邊界b處等效地震力Fb，此時Fl=0，這一輸入方式為模型B－I。類似的，模型L表示僅在邊界l處輸入等效地震力。

另一種地震動輸入方式是只考慮地震波在下臥半無限空間內的傳播，忽略側邊界處自由場運動效應。因此等效地震力僅施加在底部b，而忽略側邊界處的地震荷載Fl。這一模型可由方程（3）描述：

式中各符號的含義與式（2）相同。這一模型在文中稱作模型B－II。

式（2）和式（3）中的等效地震力可通過子結構法或直接法求解［15］。子結構法考慮了無限介質的動力特性，因此較直接法可得到更合理的等效地震力。文中故采用子結構法求解近場－遠場交界面處的等效地震力。注意，雖然式（2）和式（3）中均在近場底部施加地震荷載，但是，模型B－I假設地震波在整個自由場中傳播。在成層場地中考慮各介質間動力相互耦合，此時場地底部等效地震力Fb為：

式中：自由場運動U可根據地震波實際傳播路徑求解；?為近場和遠場交界面的底部；σ為?處位移對應的應力；為變形矩陣。而模型B－II假設地震波僅在下臥層中傳播，此時忽略了成層介質與下臥層的動力耦合對等效地震力的貢獻。因此，模型B－II中等效地震力F*b通過下述方程求解：

2 人工邊界和等效地震力

文中采用比例邊界有限元法［11］模擬近場與遠場的動力特性。比例邊界有限元法結合了有限元和邊界元的優點。它僅需離散單元的邊界，因此使得計算維度降低一維。比例邊界有限元法詳細推導過程參見文獻［11，16］。相對于比例中心（ξ=0）等比例縮放單元邊界，可獲得比例邊界單元，如圖2所示。具體地，比例邊界有限單元的幾何特性可描述為：

圖2 比例邊界有限元法模擬近場與遠場Fig.2 Modelling of near field and far field in the scaled boundary finite element method

式中：ξ和η分別是比例邊界坐標系中徑向和環向坐標；x和y是笛卡爾坐標系下單元邊界點的坐標；而x(ξ,η)和y(ξ,η)是比例邊界有限坐標下的節點坐標；N為形函數。近場中比例邊界有限單元滿足ξ≤1，而無限域中單元徑向尺寸滿足ξ∈[1,∞]。比例邊界有限單元徑向解連續且精確，環向解在有限元的意義上準確［11］。坐標轉化對應的Jacobi矩陣Jb(η)為：

在比例邊界有限元法中動力剛度S滿足下述方程：

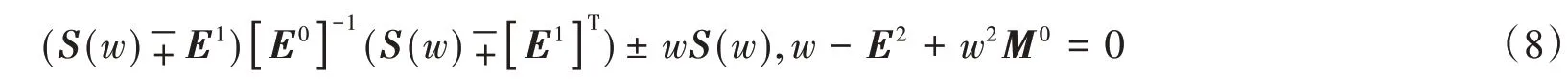
式（8）中上部符號對應近場剛度滿足的方程，下部符號則對應遠場剛度的情況。由于篇幅有限，這2個動力剛度的時域表達式參見文獻［16－17］。采用比例邊界有限元框架時等效地震力的表達式見文獻［1，14］。

3 數值算例

第1節介紹了2種不同的地震動輸入方式，即僅從底部輸入，以及從底部和側邊界同時輸入。下文分別探究這2種輸入模型對自由場動力響應的影響。首先，驗證比例邊界有限元法模擬遠場的準確性。然后，根據地震波在整個半無限介質中的傳播規律，采用模型B－I求得等效地震力，并計算相應的自由場運動。通過對比模型BL的結果分析側邊界處地震力Fl對自由場運動的影響。最后，假設地震波僅在下臥半空間介質中傳播，根據模型B－II實現地震動輸入，通過比較模型B－I、模型B－II以及解析解，探尋2種地震動輸入模型之間的關系。

3.1 半空間介質表面受壓計算

文中首先考慮了各向同性彈性半空間介質表面受壓問題，旨在驗證比例邊界有限法模擬遠場的準確性。分別采用比例邊界有限元法和粘彈性邊界模擬遠場的動力剛度。設近場寬度2d和深度h=d，如圖1所示。假設該介質楊氏模量E=2.5，泊松比ν=0.25，質量密度ρ=1，因此SV波波速cs=1。在介質表面（－d，d）之間施加豎向荷載，該荷載時程曲線g(t)呈Ricker波形狀，即

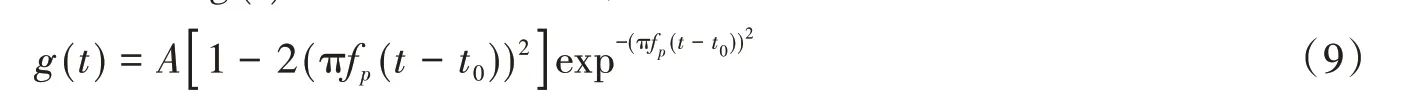
式中：A是幅值；特征頻率fp=cs/3h；時間常數t0=4h/cs；時域分析中時間步長Δt=0.1h/cs。這一信號的時程曲線與對應的傅立葉變換結果見圖3。

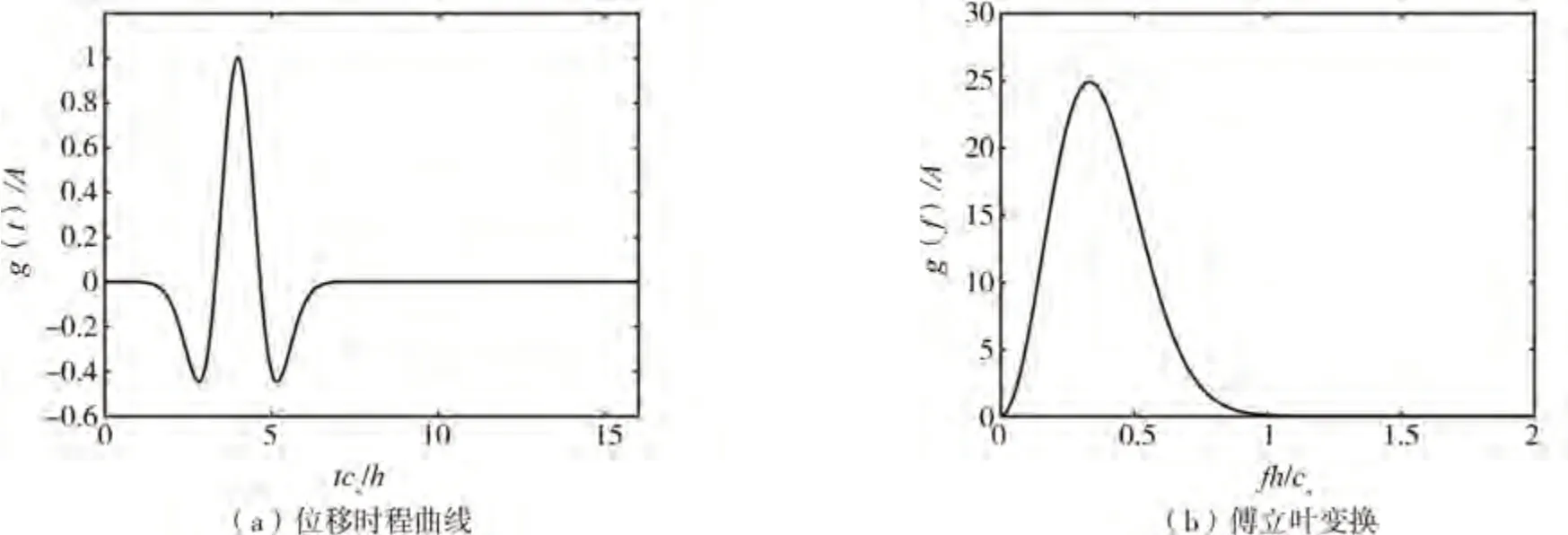
圖3 SV波的位移時程曲線和傅立葉變換Fig.3 Displacement time history and Fourier transform of vertically incident SV waves

近場由200個0.1h×0.1h的4節點單元構成。在比例邊界有限元法中，遠場的動力特性由40個2節點比例邊界單元描述，如圖4所示。在另一個模型中采用粘彈性邊界模擬遠場動力特性，該人工邊界相關參數的選取參見文獻［18］。

圖4 均質各向同性半無限介質的網格剖分Fig.4 Mesh of a homogeneous isotropic half plane

圖5顯示了采用比例邊界有限元法和粘彈性邊界時觀察點C（見圖1）的位移響應。兩者結果均與各向同性彈性半空間介質中地震波波動解析解uexact相對比。定義相對誤差R（%）為：

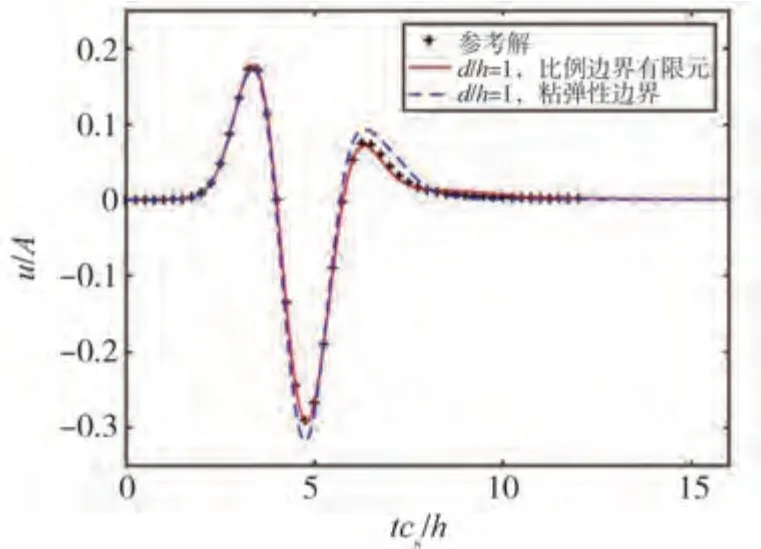
圖5 受壓半空間介質中C點位移時程Fig.5 Displacement time history at point C in a half plane subjected to a surface pressure

式中符號∣∣∣∣表示歐式范數。結果表明，采用比例邊界有限元法引起的相對誤差R=1.2%。減小時間步長Δt或增加截斷時間T可有效提高比例邊界有限元模擬無限域的精度［17，19］。相比之下，粘彈性邊界對應的相對誤差R=13.2%。這說明比例邊界有限元法可較準確地模擬無限域的動力特性，且模擬的準確程度遠高于粘彈性邊界。

3.2 側向地震力對自由場動力響應的影響

為了研究側向地震力對自由場動力響應的影響，下文考慮SV波垂直入射（θ=0°）時半空間介質波動問題。假設入射SV波為平面波，其位移呈Ricker波形狀，如圖3所示。場地條件與算例3.1相同。分別采用模型B－I，模型L和模型BL計算中心線CD（見圖1）上各點的位移時程，如圖6所示。各向同性彈性半空間介質中地震波波動解析解uexact也包含在圖6中，以作對比。理論上，模型B－I與模型L計算結果之和應與模型BL的相同。對比發現，前者對應的相對誤差R最大值約為后者的2倍。考慮到模型B－I、模型L和模型BL中僅等效地震力的大小不同，這說明數值分析系統誤差存在，且大小約為1%。由算例1可知誤差主要來源于遠場模擬。

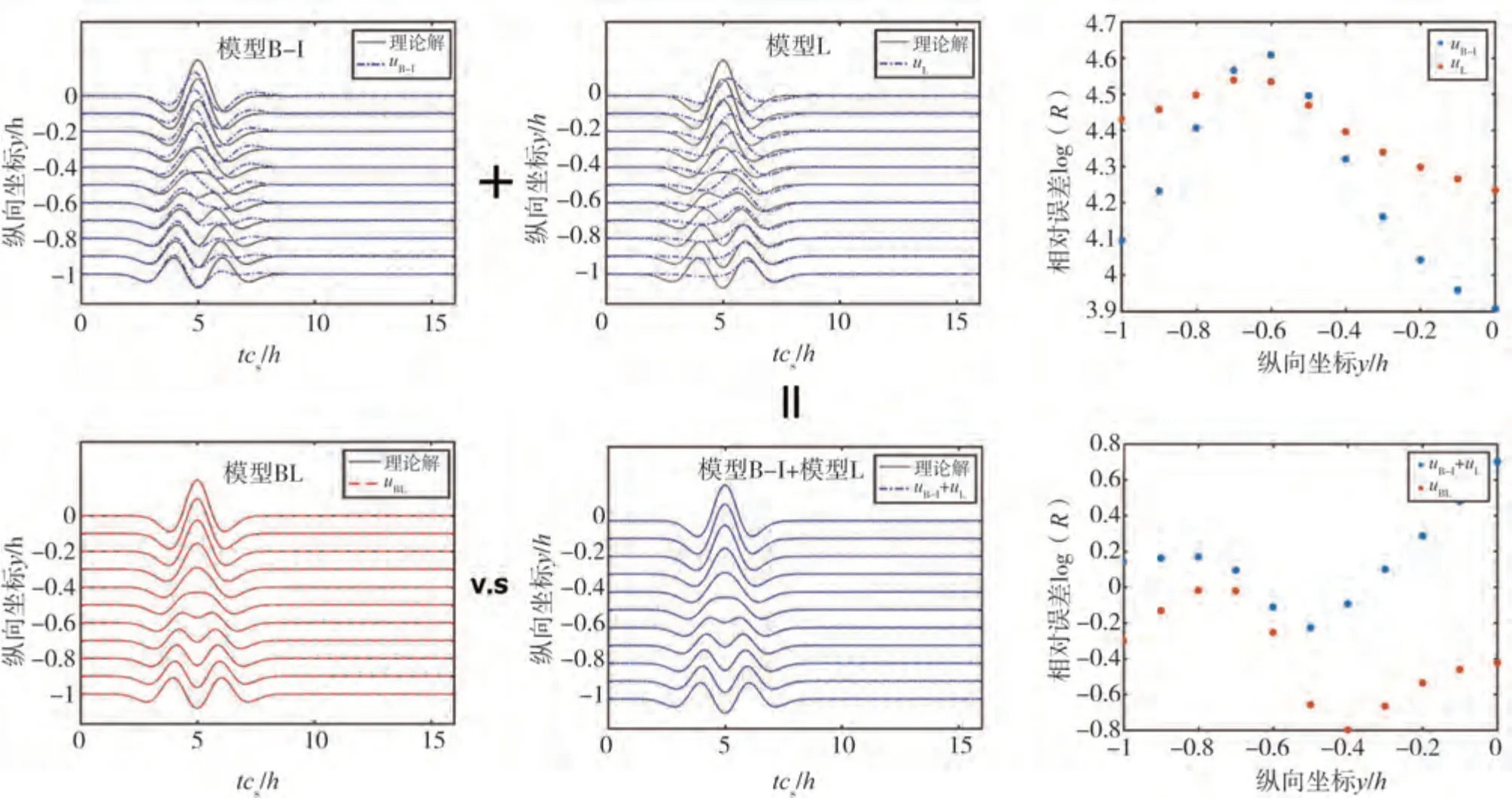
圖6 比較采用模型BL和模型B－I時自由場反應Fig.6 Comparison of free field motion using model BL and model B－I

由圖6可知，模型BL求得的計算結果與理論解的相對誤差R小于1%，而模型B－I對應的結果與理論解差別R高達99.48%。這說明單獨考慮底邊地震輸入是遠遠不夠的。雖然側邊界處地震荷載始終存在，但其對CD線上各點的影響隨著近場寬度d的增加而減小。鑒于此，文中分別選取d/h=1，5，10和18，考察不同寬度下側邊界處等效地震力對自由場動力響應的影響。圖7展現了不同寬度d下C點處位移響應ub，以及CD線上各點位移與理論解相對誤差R的箱線圖。

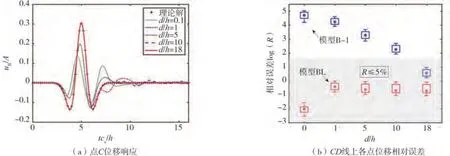
圖7 模型B－I與模型BL中位移響應比較Fig.7 Comparison of the displacement obtained from model B－I and model BL

研究表明，采用模型BL的計算結果與理論值的差別始終保持在1%以內，且該誤差與近場寬度d無關。采用模型B－I時，隨著場地寬度d的增加，底邊地震荷載引起的位移ub快速收斂于理論解。這是因為側邊界處地震荷載引起的位移ul隨場地寬度d的增加而呈現指數衰減，如圖8所示。當d增大到18h時模型B－I對應的相對誤差R小于2.7%。然而，該誤差R仍高于模型BL對應的結果0.9%。這說明側邊界處地震荷載fl始終存在，且當場地寬度d較小時,fl不可忽略。當d足夠大時，fl在一定的計算時間內無法對研究點處自由場運動產生影響，此時側邊界處地震力對自由場運動的影響可忽略不計，即模型B－I與模型BL等價。

圖8 采用模型L時位移響應Fig.8 Displacement response obtained by using model L

3.3 成層半空間介質地震波傳播

第1節中介紹了僅底部輸入時有2種可行的方案：一種是考慮地震波在整個半無限介質內的傳播，即模型B－I；另一種則假設地震荷載僅與下臥層相關，即模型B－II。下文討論成層介質中地震波傳播路徑對等效地震力計算結果的影響。比例邊界有限元法已用于模擬多層介質中地震波傳播問題［19］，這里僅考慮兩層介質的情況，如圖9所示。下臥層近場尺寸取為2d×h1，且有h1/h=1/3。假設成層介質和下臥半空間介質的材料特性相同。其他條件與算例3.2相同。

根據地震波在半空間介質中的傳播規律［20］，SV波垂直入射時下臥層內D點（見圖9）的應力理論解為：

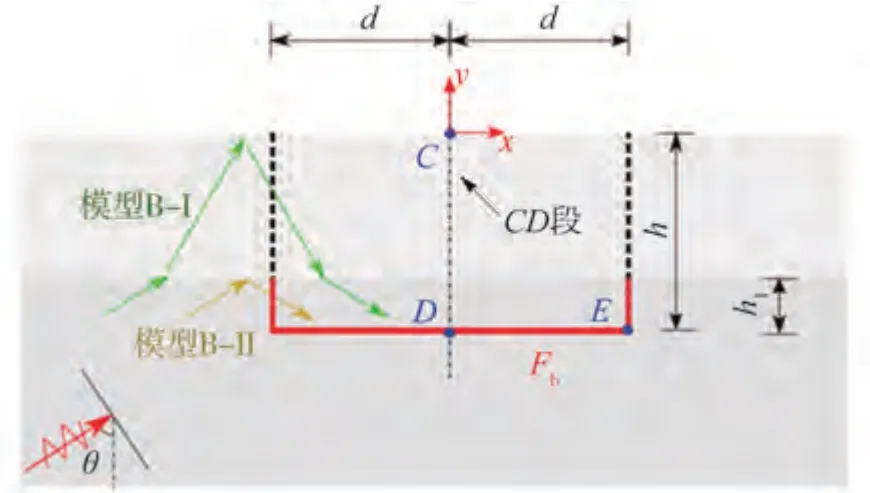
圖9 底部輸入等效地震力模型Fig.9 Models of equivalent seismic input applied at the bottom of the near field

考慮到SV波垂直時該介質水平方向上應力均勻分布，且單元網格尺寸均為0.1h，因此D點水平向地震力的理論解為：

為驗證數值方法的正確性，圖10（a）對比了等效地震力的數值解和理論解。結果表明，在場地底部中點D處，2種地震動輸入方法得到的數值解與理論解吻合很好。

圖11顯示了采用模型B－I和模型B－II時CD線（見圖9）上各節點的位移時程與相對誤差R。結果表明，這2種底部輸入模型均與理論解存在顯著差別。這說明在場地尺寸較小時，側邊界處地震力不可忽略。另外，采用下臥層剛度的模型B－I引起的相對誤差較模型B－II的大，前者約為后者的1.5倍。為進一步解釋原因，圖10（b）給出了采用不同模型時場地角點E處的等效地震力。由圖可知，模型B－II對應的等效地震力約為模型B－I的1.47倍。這兩者等效地震力之差是由成層介質和下臥層的動力耦合造成的（見式（4）和式（5））。因此，相對于地震波在整個自由場的傳播，考慮地震波在下臥層的傳播減少了由于場地介質動力耦合產生的額外地震力，從而減小了對自由場運動計算結果的影響。

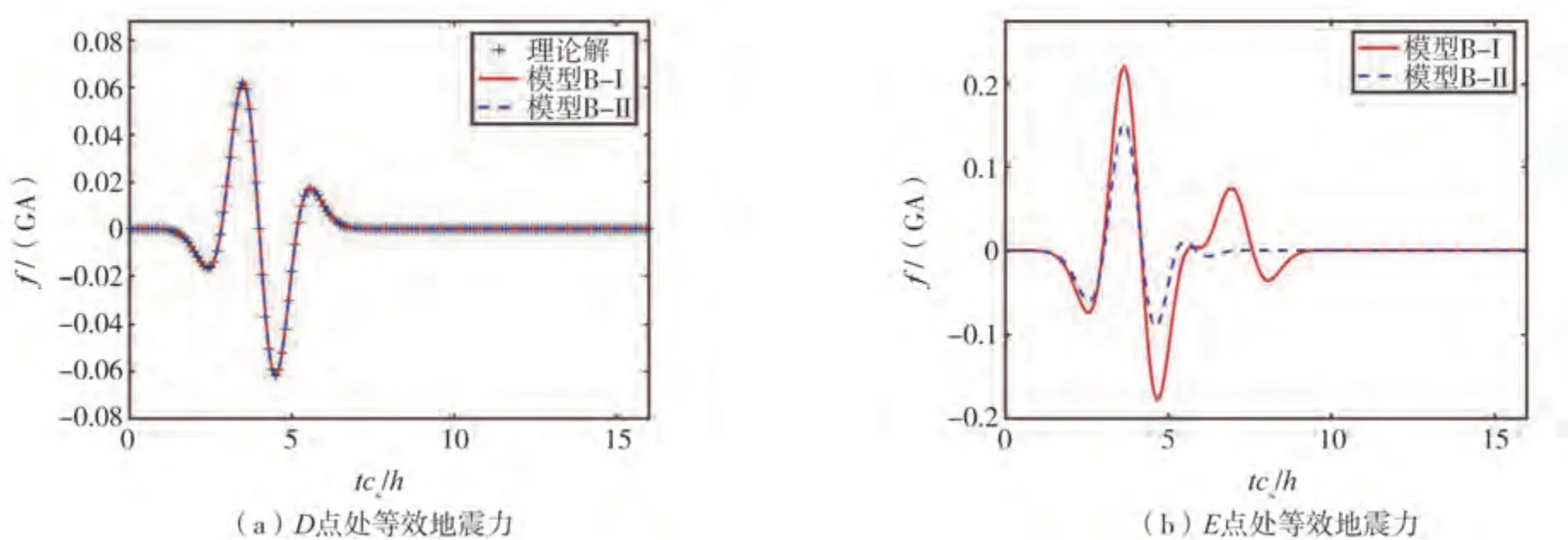
圖10 比較模型B－I與模型B－II等效地震力Fig.10 Comparison of equivalent seismic forces obtained from model B－I and model B－II

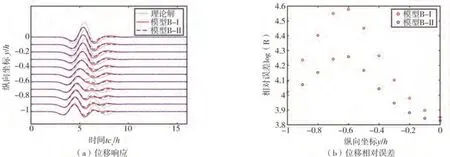
圖11 比較模型B－I與模型B－II中CD線上各點位移響應Fig.11 Comparison of displacement response along CD in model B－I and model B－II

4 結論

文中采用理論分析和數值模擬的方法研究了2種不同的地震動輸入方式：一種是僅從近場底部輸入，另一種是同時從近場的底部和側邊界處輸入。研究以平面SV波垂直入射自由場為例，首先利用比例邊界有限元法嚴格模擬了幾何無限介質的動力特性；基于此，結合理論分析和數值模擬方法，計算了2種模型對應的自由場運動以及等效地震力。結果表明：

（1）側邊界處等效地震力對自由場運動的影響不可忽略，該影響隨著近場寬度的增加而呈指數降低趨勢；

（2）在本研究中，當均質彈性近場的寬深比（2d/h）大于36時，采用底部輸入模型得到的自由場運動數值解與理論解的誤差在5%之內。當在底部、側邊界同時輸入等效地震力時，求得的計算結果與理論解的誤差與場地尺寸無關。

（3）在底部輸入地震動模型中，相比于考慮地震波在整個自由場的傳播，假設地震波在下臥層傳播減小了由場地各介質耦合產生的附加地震力，從而減小了自由場運動的求解誤差。