對剛體滾動過程中摩擦力做功問題的探討

鄭 金

（遼寧省凌源市職教中心，遼寧 朝陽 122500）

1 引出問題

原題.如圖1所示，半徑為R的圓柱體在重力作用下沿斜面連滾帶滑地從頂端運動到底端，設斜面的長為L，斜面對圓柱體的滑動摩擦力為f，試研究下滑過程中滑動摩擦力對圓柱體所做的功.

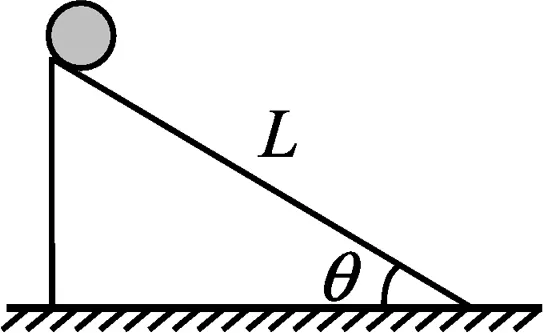
圖1

原解：將摩擦力f平移到圓柱體的中心，同時附加力偶矩M＝f R的作用.平移到圓柱體中心的力f在運動過程中做的功等于－f L.設在運動過程中圓柱體轉過的角度為φ（由于有滑動，則φR＜L），可知附加力偶矩做的功為Mφ＝f Rφ.所以，摩擦力對圓柱體做的功為W＝－f L＋f Rφ＜0.

探討：原題及原解來自文獻［1］.對于原題，是一道關于剛體在滾動過程中摩擦力做功的問題，但在以往的高中物理競賽中，有關剛體滾動的試題很少涉及摩擦力做功的計算，由此看來，原題的難度是比較大的.此外，對于原解，雖然算出的功為W＝－f L＋f Rφ，但不是最終結果，因為角度φ是未知量，還需求出角度φ代入.

2 解決問題

在原題中提到“連滾帶滑”，這種運動形式屬于非純滾動，只有對非純滾動才能談論“滑動摩擦力做功”.鑒于此，首先探究圓柱體發生非純滾動的條件，然后對摩擦力做的功給出3種求解方法.

2.1 推導圓柱體在斜面上做非純滾動的條件

設斜面的傾斜角為θ，發生純滾動的圓柱體側面受到靜摩擦力大小為f′，質心加速度大小為a，由質心運動定理有mg sinθ－f′＝ma.

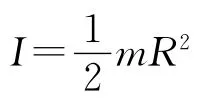
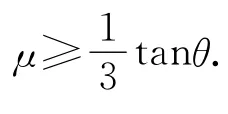
2.2 推導相對滑動路程的關系式及其含義

滑動摩擦力對圓柱體做功，包括兩方面，即滑動摩擦力f阻礙圓柱體前進，做負功；同時，滑動摩擦力相對于質心提供一個轉動力矩，使圓柱體加速轉動，做正功.設質心平動路程為s，側面轉動路程為s1，相對滑動路程為s2，則摩擦阻力對圓柱體做的功為W0＝－fs，摩擦動力對圓柱體做的功為W1＝fs1，可知摩擦力對圓柱體做的總功為

W＝W0＋W1＝－f（s－s1）.

滑動摩擦力屬于非保守力，由功能關系可知，滑動摩擦力做功的過程，是機械能減少的過程，即內能增加的過程，因此滑動摩擦力做功的絕對值等于摩擦生熱即內能W＝Q＝fs2.

聯立方程可知相對滑動路程為s2＝s－s1.這表明，在圓柱體質心平動速度與側面切向速度方向相反的情況下，相對滑動路程等于質心平動路程與側面轉動路程之差.其中平動路程是假設圓柱體不轉動只平動時側面滑動的路程，即質心運動的路程；轉動路程是假設圓柱體不平動只轉動時側面滑動的路程，即側面相對于質心轉動的路程.

值得注意的是，圓柱體克服摩擦力做的功并不等于產生的熱量，只有總功的絕對值才等于熱量.這如同光滑水平面上的平板車與車上的物塊發生相對滑動的過程中摩擦力做的總功，即相互作用的一對摩擦力對系統做的功為負值，其絕對值等于熱量，等于摩擦力大小與相對滑動路程之積.

2.3 計算滑動摩擦力做的功

下面給出不同于原解的3種方法.

解法1：間接計算相對滑動路程.

當圓柱體發生滑動時，質心的加速度大小為

a＝g sinθ－μg cosθ.

由運動學公式可得運動時間為

其中動摩擦因數滿足f＝μmg cosθ，可知

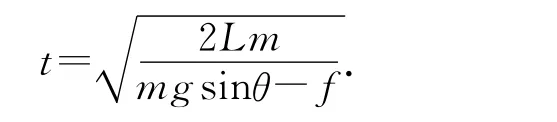
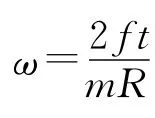
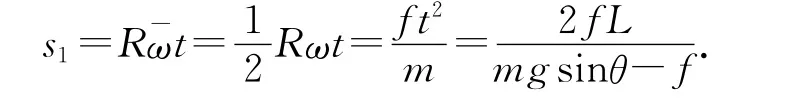
因此相對滑動路程為

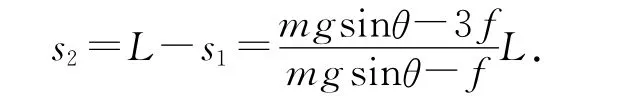
滑動摩擦力做功為

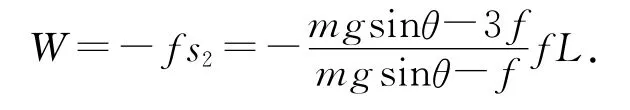
解法2：直接計算相對滑動路程.

由轉動定理可知圓柱體轉動的角加速度為

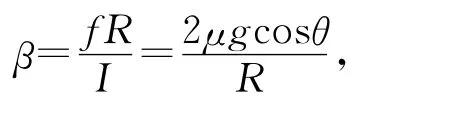
則側面相對于質心轉動的切向加速度為

a1＝βR＝2μg cosθ.

在接觸面處，切向加速度方向沿斜面向上，質心加速度方向沿斜面向下，根據相對滑動加速度等于質心平動加速度與側面切向加速度的矢量和，得

a2＝a－a1＝g sinθ－3μg cosθ.由于初速度為0，則相對滑動的路程為

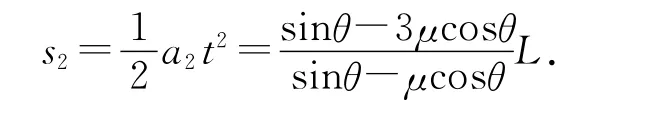
利用f＝μg cosθ可知摩擦力做的總功為

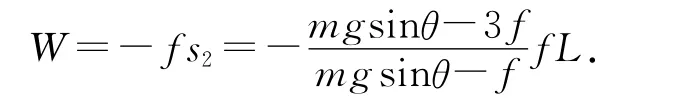
解法3：應用能量守恒定律計算熱量.

圓柱體的動能包括質心平動動能與繞質心的轉動動能.由能量守恒定律可知摩擦產生的熱量為

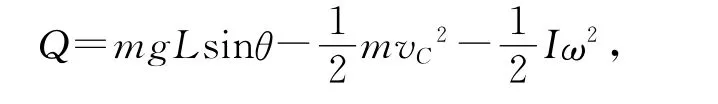
其中vC＝at，ω＝βt.由功能關系知滑動摩擦力做功W＝－Q.

3 結語

綜上可見，圓柱體在斜面上滾動過程中的相對滑動路程是一個很抽象的物理量，不僅與軸線平動的路程有關，還與側面相對于軸線轉動的路程有關.若圓柱體側面相對于質心轉動的路程與質心平動的路程不相等，則相對滑動路程不為0，發生非純滾動.若在接觸點處的切向運動方向與質心平動方向相反，則相對滑動路程等于剛體質心平動路程與側面轉動路程之差的絕對值；若在接觸點處的切向運動方向與平動方向相同，則相對滑動路程等于剛體質心平動路程與側面轉動路程之和.為了計算相對滑動路程，關鍵是把剛體的運動分解為質心的平動與側面繞質心的轉動，兩個分運動都是勻變速運動，利用運動學公式即可求出各自的路程.但要注意側面的“勻變速”運動是曲線運動，而且兩個分運動的加速度不同.滑動摩擦力做的功為負值，包括兩方面，即滑動摩擦力阻礙圓柱體的平動做負功以及使圓柱體加速轉動做正功，總功即二者的代數和為負值，其絕對值為圓柱體的機械能變化量，在數值上等于系統產生的熱量，等于摩擦力大小與相對滑動路程之積.