DC-DC全橋電路軟啟動控制方法

李源升，薛夢嬌，胡朋舉

(國網新疆電力有限公司超高壓分公司，新疆 烏魯木齊 830092)

隨著社會能源需求的增長，社會高速可持續發展的能源結構不再僅僅依靠單一的化石能源，為了應對這一問題，我國一直積極發展新能源，新型清潔能源是今后的發展趨勢，當今能源結構多樣化越來越明顯。而人類生產生活所需求的載能體也呈現多樣化趨勢。為了促進能源網絡的發展，實現社會的可持續發展，能源互聯網成為目前研究能源形式的熱點[1]。

傳統的橋式直流變換器是將輸入側能量傳輸到輸出側，而且是單向的能量流動。只能將能量由一端向另外一端傳輸，而雙向DC-DC變換器可以在同一設備上實現能量的雙向傳輸。早在20世紀80年代初，為了減輕人造衛星太陽能電源系統的體積和質量，就有學者提出用雙向Buck/Boost 變換器與太陽能電池的組合代替蓄電池供電[2]。華中科技大學研究團隊針對電力電子變壓器對配電系統的控制性能及動態特性的影響進行了理論與仿真研究[3]。清華大學研究團隊針對柔性直流配電網的直流固態變壓器方案進行了研究，并對其基本結構、控制策略及能量管理系統做了分析驗證[3]。趙爭鳴教授提出了直接基于能量平衡關系的電能路由器控制策略，并對其正確性進行了試驗驗證[4]。

目前研究熱點主要集中在改進的變換器拓撲結構及移相控制方法，但是還存在許多不足[5]。前文重點研究方向在于，盡量減小系統的回流功率，降低開關管的單管電壓應力、電流應力等方向，鮮有分析系統啟動過程中出現大電流的現象。本文在單移相控制的基礎上針對啟動過程中出現的大電流進行分析[6-12]，提出改進方法，解決系統啟動過程中所出現的大電流現象。減少了啟動過程中出現的大電流，改善了系統的可靠性和安全性。同時使用數字處理器實現雙向DC-DC變換器的移相閉環控制。

1 DC-DC全橋電源系統控制器設計

1.1 DC-DC全橋電源的工作原理

圖1中，變壓器兩側全橋每個橋臂的上下管之間都是180°互補導通，斜對角2只開關管之間的脈沖信號相同。變壓器左側全橋逆變輸出的電壓均為固定占空比的雙極性方波，右側全橋折算到變壓器左側的電壓也為固定占空比的雙極性方波，兩側方波之間有相角差。單移相控制方式就是通過控制變壓器兩側繞組之間的移相角來實現功率的大小變化和方向的流動。

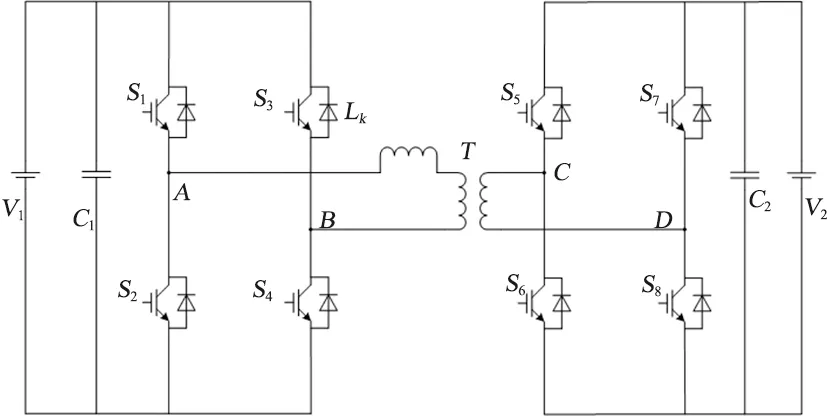
圖1 雙向全橋拓撲結構

單移相下的能量正向流動中，DAB模塊是從左側流向右側，即UAB的相位超前UCD；同理，單移相下的能量負向流動中，能量從右側流向左側，即UAB的相位滯后UCD。為了便于分析，進一步簡化全橋DC-DC電路的變壓器，可以得到變壓器的等效電路，同時圖1所示的全橋DC-DC電路可以簡化為圖2所示的DAB能量流動電路模型[13-15]。由圖2可知，全橋DC-DC電路的能量雙向傳遞與儲存主要是靠這個功率電感以及變壓器內部的漏感。通過圖2可以對單移相控制下DAB電路的正向能量流動的工作模式進行具體分析。

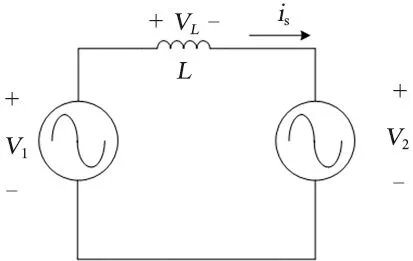
圖2 DAB的等效電路模型

在單移相控制下，一個開關周期內DC-DC變換器的穩態電感電流可以分為4個階段[16-17]，若令t0=0，則t1-t6時刻可以分別表示為t2=DT，t3=T，t5=(1+D)T，t6=2T，D為移相占空比，0≤D≤1。根據伏秒平衡原理，即電感電流的對稱性，即iL(t0)= -iL(t3)。

(1)

(2)

式中：V1和V2分別為變換器輸入側和輸出側的電壓；n為變壓器變比；L為等效電感，是串聯電感和變壓器漏感之和。則有：

(3)

(4)

設交換器的電壓調節比k=V1/V2，開關頻率fs=1/(2T)，則有：

(5)

(6)

相應可得到單移相控制方式下傳輸功率為

(7)

則有DC-DC變換器的輸出平均電流為

(8)

流經變換器等效電感L的電流峰值為

(9)

通過式(9)可知，傳輸功率的范圍會隨移相占空比改變而發生改變。為了便于分析，將傳輸功率標幺化，定基準值為

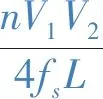
(10)

則此時傳輸功率的標幺值為

(11)

1.2 DC-DC全橋電源的軟啟動

當從低壓側啟動時，電容C2的電壓為0，漏感電流會出現較大的沖擊。電路在半個周期內占空比由0逐漸增加到0.5，因此其半周期的伏秒值為

(12)

式中：n為變壓器的匝比，n=n2/n1；D為移相比；T為半個開關周期。

由此可見，從0開始緩慢增加占空比D，電壓半周期伏秒值從0增加，從而有效減小漏感沖擊電流。該啟動方式的波形如圖3所示，即改變加在各個開關管上的驅動脈沖寬度，在系統未達到穩定前，動態調節驅動脈沖寬度，限制電感電流的上升時間，使電感電流工作在DCM模式，從而將電流限制在一定范圍內，有效降低單個開關管的電流應力。

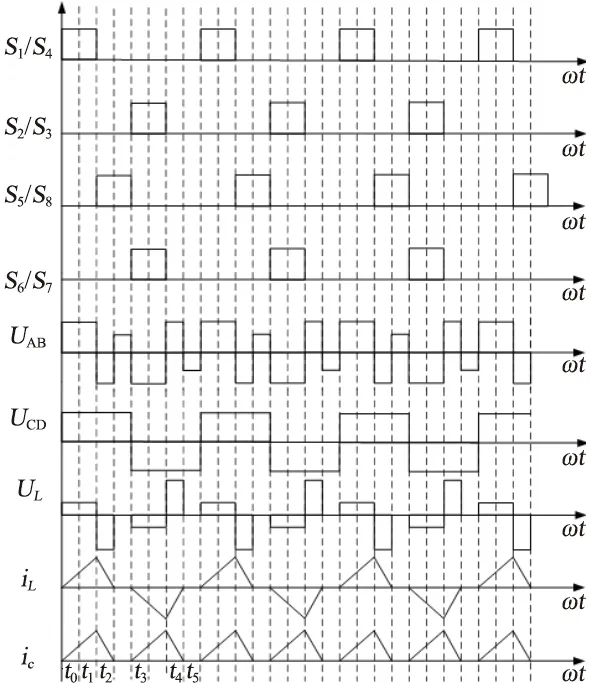
圖3 窄脈寬啟動過程

1.3 死區影響分析及補償措施

在變換器工作時，為了避免同一橋臂的上下開關管同時導通造成短路，致使電路無法正常工作，一般要設置一個死區時間，這對電路工作的可靠性十分重要，但是死區會造成波形變化和傳遞功率大小變化。以功率正向傳輸為例，設置一個死區時間tdb。當i(t0)<0且i(t2)<0時，兩側工作模態如圖4所示。D為DAB模塊的低壓側原邊全橋與高壓側副邊全橋開關管之間的驅動信號的移相比，由圖4可知，t0-t2時刻，DAB模塊的電流在t0時刻之前，it0<0,t0時刻后，變壓器原邊電流經S1、S4上的體二極管，此時電路原邊側輸出的電壓UAB與原邊側的輸入電壓相同，即UAB的高電平比S1、S4的驅動脈沖提前死區時間tdb。it2<0，高壓側副邊電路的開關管S6、S7的二極管需要進行續流，同時開關管S5和S8不導通。因此，死區影響下的實際移相比為Dt=D+tdb/T。因此，當移相比D=0 時，由于死區時間的存在，Dt=tdb/T，系統仍會輸出功率。當i(t0)<0且i(t2)>0時，即前文分析的正常穩定工作時的情況，此時死區時間對實際的移相占空比沒有影響，Dt=D。

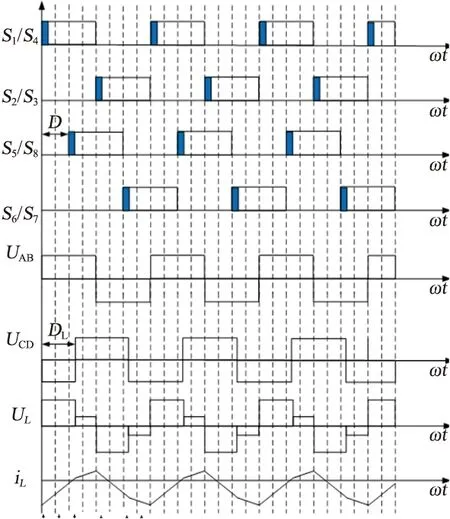
圖4 死區時間對于移相比的影響(i(t0)<0, i(t2)<0)

當i(t0)>0且i(t2)>0時，兩側工作模態如圖5所示。實際的移相占空比為Dt=D-tdb/T。由于i(t0)>0，故在S1、S4沒有給驅動信號時，原邊電流通過開關管S2、S3并聯的二級管續流，UAB的高電平與S1、S4的驅動脈沖相比，減少了死區時間tdb，而由于i(t2)>0，故在S5、S8沒有給驅動信號時，副邊的電流通過開關管S6、S7的體二極管進行續流，UCD的高電平與S5、S8的驅動脈沖同步，因此，死區影響下的實際移相比Dt=D-tdb/T，實際移相比小于理論值。

圖5 死區時間對于移相比的影響(i(t0)>0, i(t2)>0)

系統仿真的輸出功率是完全理想情況下，然而實際開關管的死區影響輸出功率，而且隨著電流變化而改變，當死區時間tdb越來越大時，死區影響將增加。因此需要采取補償措施。DAB模塊工作在i(t0)<0且i(t2)<0時，加上死區的實際移相比為Dt=D+tdb/T，此時應使S5、S7的驅動信號相對于S1、S3的驅動信號滯后，時間比理論減小tdb即可。DAB模塊工作在i(t0)<0且i(t2)>0時，實際移相比為Dt=D，此時開關管不用死區補償，而且開關管容易實現軟開關狀態。DAB模塊工作在i(t0)>0且i(t2)>0時，實際的移相比為Dt=D-tdb/T，此時應使S5、S7的驅動信號相對于S1、S3的驅動信號滯后時間比理論增加tdb即可。

1.4 電壓閉環控制

雙向DC-DC全橋電路的開關頻率大，普通設備難以在極小時間內同時采樣得出電壓、電流的波形，采樣難度大。因此本文的控制方式采用電壓單閉環的控制方式，將采樣電壓作為閉環的被控對象，利用改變占空比來影響電壓的大小，從而影響電流大小，進行控制整個電路的穩定。

由前文有輸出與輸入控制量之間傳遞函數為

(13)

試驗中參數取值為U1=48、n=8、fs=25 kHz、C2=470 μF、Ro=250 Ω、D=0.2、L=8 μH。則加入調節器前，系統開環傳遞函數為

(14)

圖6的Bode圖是根據式(14)中傳遞函數得出，在系統加入調節器前，該系統是穩定系統，但可以明顯看出在低頻段時，系統的増益過小，從而導致系統穩態精度不佳，存在穩態誤差。而系統的動態響應因截止頻率過低而過慢。對于改善系統的性能有多種方法，本論文通過加入快速PI調節器，利用Bode圖進行系統優化。為消除低頻情況下的缺點，PI調節器零點接近系統的低頻極點，能夠解決低頻極點對系統的影響。

加入快速PI調節器后的系統Bode圖如圖7所示，PI調節器含有積分項，一定程度上提高了系統穩態精度，系統動態響應快。經過實際仿真驗證，得出Kp=0.01，Ki=90。

1.5 系統控制結構

經過對DAB模塊的工作原理進行分析，在單移相控制的基礎上進行了詳細分析，并且搭建了1臺1 kW的雙向DC-DC變換器樣機，為了驗證隔離性雙向DC-DC電路在此控制方式下的正確性，具體的技術要求和系統參數如下：DAB模塊的額定輸出功率Pn=1 kW；直流母線電壓(低壓側)VL=48 V，變化范圍48±10%；直流母線電壓(高壓側)VH=400 V，變化范圍400±10%；開關頻率fs=25 kHz；低壓側母線電容C1=4700 μF/100 V；高壓側母線電容C2=470 μF/450 V。

控制系統的整體控制框如圖8所示，包括主功率電路、控制電路、調理電路、驅動電路等。

圖6 系統開環Bode圖

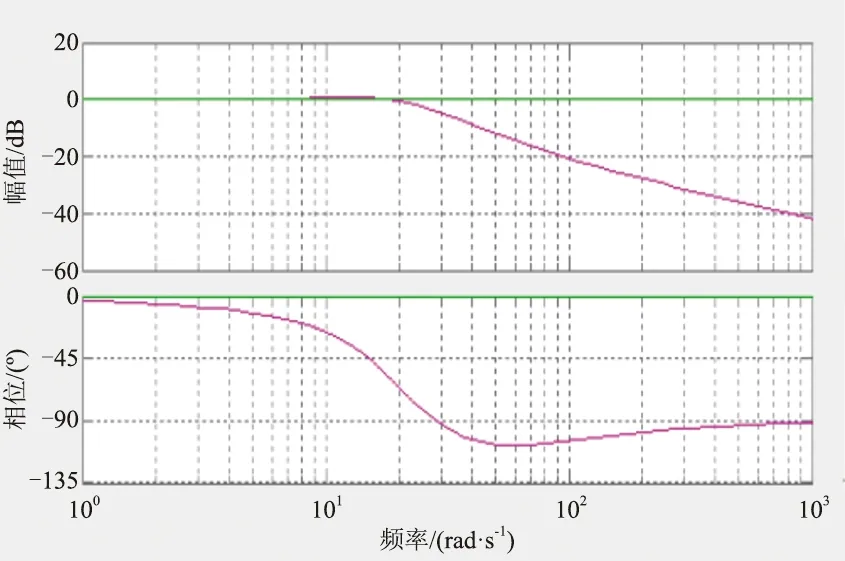
圖7 系統補償后Bode圖

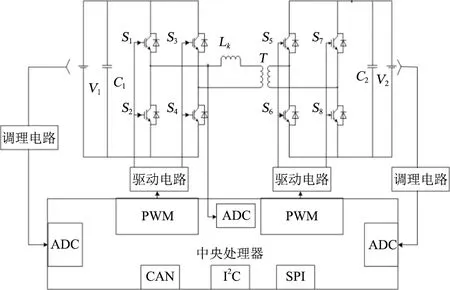
圖8 系統控制結構框圖

2 仿真及試驗結果分析

2.1 PLECS仿真及結果分析

本系統以25 kHz DC-DC電源為背景進行仿真研究。采用上述方案構建DC-DC電源的閉環控制系統，在PLECS仿真環境下進行仿真分析。系統的仿真參數如下：輸出電壓380 V，直流母線電壓VDC=48 V，電感L=10 μH，電容C=440 μF，三角載波頻率fs=25 kHz。外環調節器的PI參數：kp1=1.75，ki1=20。

對所設計的DC-DC電源分別做啟動(負載電阻R=250 Ω)和穩態過程負載(負載電阻R=250 Ω)仿真。

圖9與圖10對比了系統在啟動和穩定狀態下兩側全橋輸出側電壓波形，啟動過程中，兩側電壓基本同向，從而限制啟動過程中的沖擊電流。在系統穩定后，系統以一個固定的移向角運行。

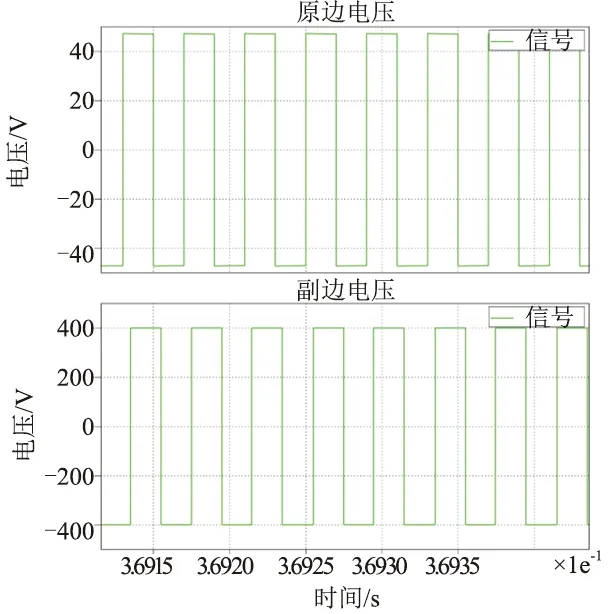
圖9 啟動過程波形

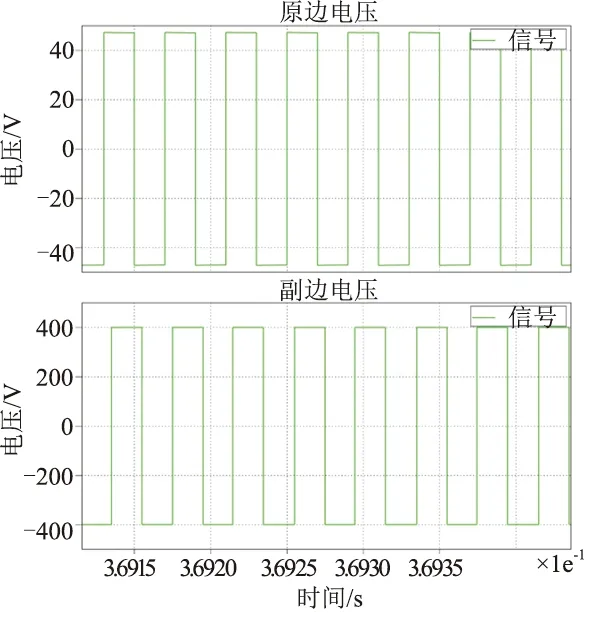
圖10 穩態輸出波形

圖11與圖12對比了系統在啟動和穩定狀態下變壓器兩側電壓和電流波形，啟動過程中，副邊電壓為逐漸增加的方波，流過變壓器的電流也由三角波逐漸變為梯形波，系統最后逐步穩定下來，在負載不變的前提下，以固定移相角運行。

圖13、圖14與圖15分別為軟啟動電壓電流波形、軟啟動功率電感電壓波形與軟啟動狀態下負載突變時電壓波形。由圖13可知，軟啟動狀態下電壓電流緩慢增加，有利于減少電壓電流突變導致的電流過大或者短時電壓過大對開關管的沖擊，一定程度上減少了紋波電流對開關電源的沖擊影響。

由圖14可知，電感電壓緩慢增大，減少了電壓突變對電路穩定性造成的影響，一定程度上減少了電壓對開關管及供電電源沖擊，使其壽命增加。

圖15為負載突變時電壓波形，由圖15可知，在軟啟動作用下，系統的超調僅有0.92%。調節時間較短，而且最大峰值電壓只超出額定電壓2.8 V，對開關管的沖擊基本可以忽略不計，驗證了該啟動方式具有良好的快速性能。

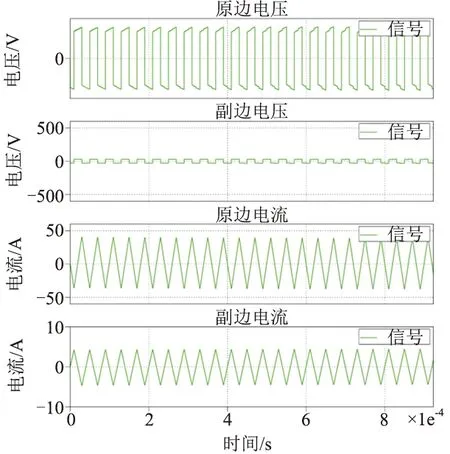
圖11 啟動過程時電流波形

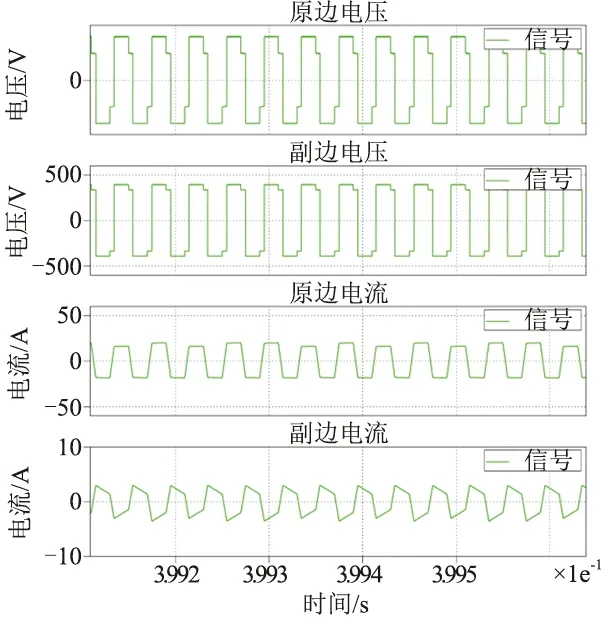
圖12 穩態時電流波形

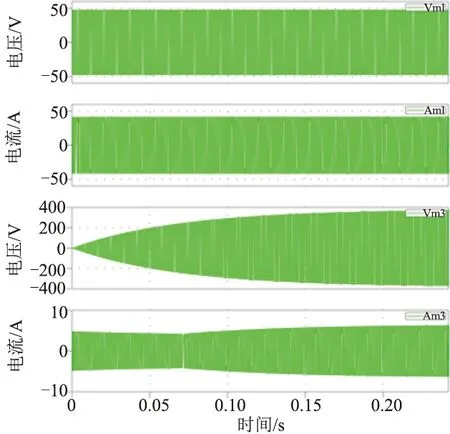
圖13 軟啟動電壓波形

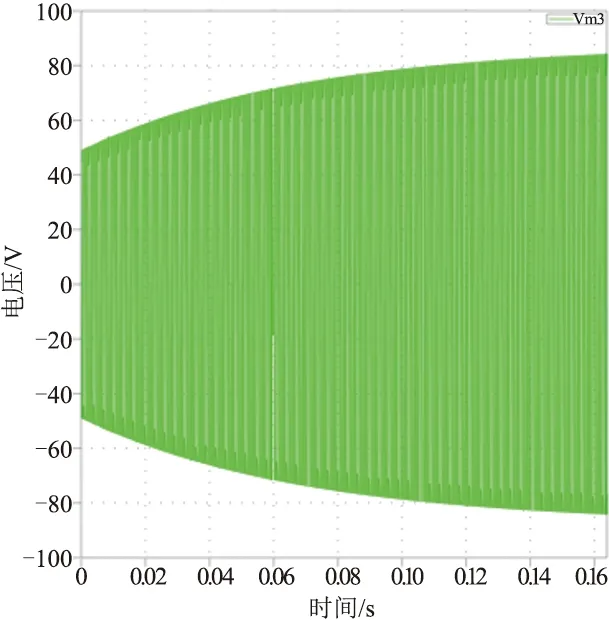
圖14 軟啟動功率電感電壓波形

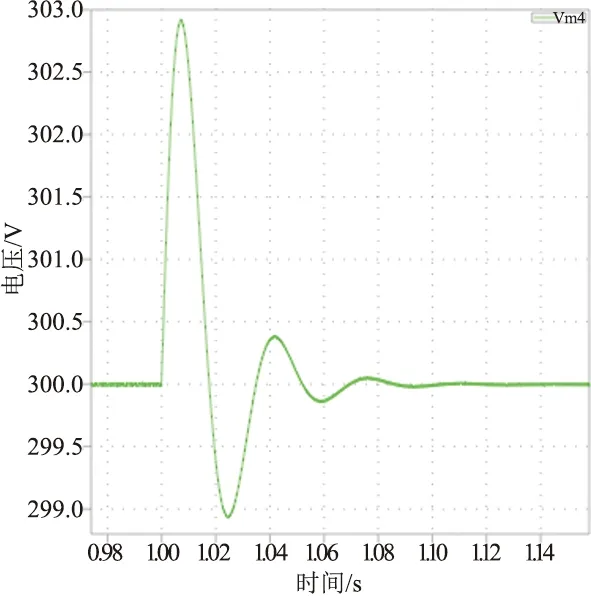
圖15 軟啟動狀態下負載突變時電壓波形

2.2 試驗結果分析

本系統以DSP為核心，使用TI官方提供的編程軟件Code Composer Studio 6.0進行軟件算法的編程，實現對全橋DC-DC的閉環控制。利用上述控制方法搭建試驗平臺，試驗參數如表1所示，圖16為試驗平臺。

表1 試驗主電路參數

試驗波形如圖17所示。圖17為開關管實現ZVS軟開關；圖18為直接啟動與軟啟動波形。圖17為開關管ZVS(zero voltage switch)導通波形，藍色為驅動信號波形，綠色為相應IGBT上CE之間電壓波形，由圖17可知，IGBT在未給驅動信號前，兩側電壓已經為零，因而，該開關管可以實現零電壓導通，開通損耗幾乎為零。功率回路中的8個開關管均可實現零電壓導通。

圖18為系統正常啟動時系統輸出電壓波形，系統輸出電壓逐漸穩定到400 V。

圖16 試驗平臺

圖17 開關管實現ZVS軟開關

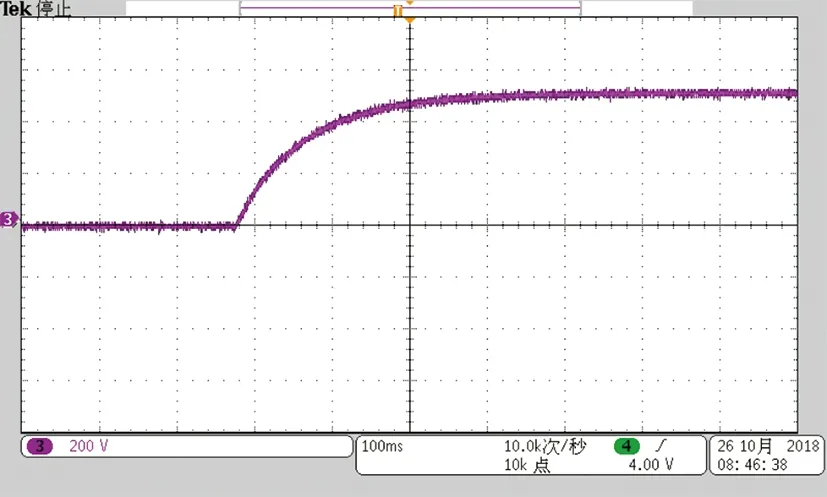
圖18 直接啟動電壓波形

圖19為系統軟啟動波形，在啟動的前半段，由于采用了軟啟動策略，限制了電路中的電流，也就限制了高壓側電容的充電電流。

由圖19可知，軟啟動過程中，前半部分由于充電電流被限制，電壓緩慢上升，待達到設定電壓后，系統進入閉環控制狀態，將PWM波的占空比固定在0.5，動態調節移相角度。穩定輸出電壓波形。使電壓逐漸穩定到400 V。系統穩定時間稍長，但相比較于直接啟動，限制了系統的沖擊電流，減小了系統中的電流應力。保證了系統運行的安全性。

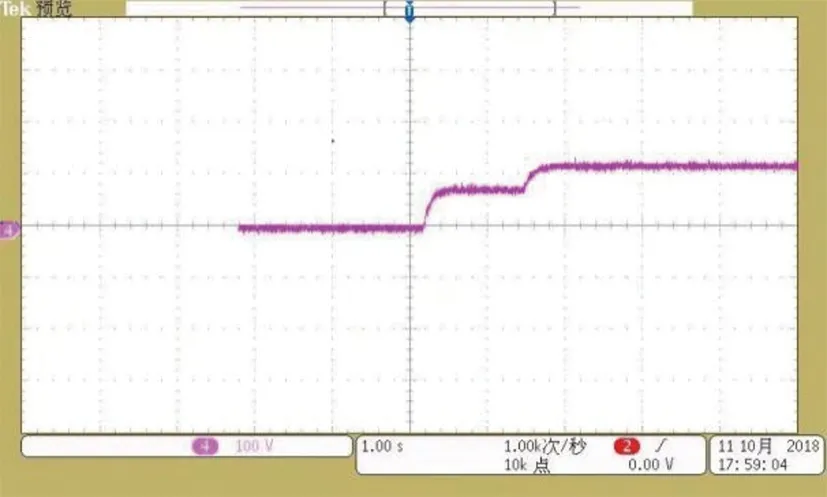
圖19 軟啟動電壓波形

3 結語

本文以單相全橋DC-DC電源作為研究對象，對雙向全橋直流變換器進行建模，得出系統的傳遞函數，對開環系統進行補償，有效改善了系統的穩定性。針對系統啟動過程中出現的短暫沖擊電流，分析了沖擊電流的成因，提出了動態改脈寬的軟啟動控制方式，較串電阻、加輔助回路等方式具有成本低，控制簡單等優點。系統進入穩態運行后，采用閉環控制策略維持電壓穩定。最后對實際工程中出現的死區對系統輸出的影響進行了具體分析，并針對具體情況，提出了相應的補償措施。此外，系統仿真和試驗結果表明，本文采用的控制方法有效可行，提高了電源的輸出精度及響應速度。