基于健康監測的重載鐵路連續剛構橋活載撓度可靠度評估

談遂， 王翔

(1. 高速鐵路建造技術國家工程研究中心， 長沙 410075； 2. 中南大學土木工程學院， 長沙 410075；3. 橋梁結構健康與安全國家重點實驗室， 武漢 430034； 4. 中鐵大橋科學研究院有限公司， 武漢 430034)

主梁撓度是反映橋梁結構剛度的重要指標，是反映橋梁結構服役性能的關鍵參數之一[1]。近年來，隨著健康監測技術的發展，大量橋梁安裝有撓度監測系統，也涌現出了一些先進的主梁撓度監測方法，例如連通管[2]、機器視覺[3]、毫米波雷達[4]、全球導航衛星系統(global navigation satellite system，GNSS)[5]等。運營期橋梁主梁撓度的獲取越來越便利，監測數據精度也得到了大幅提升。如何有效利用主梁撓度長期監測數據進行橋梁服役性能評估，是橋梁健康監測領域迫切需要解決的問題之一[6]。

基于可靠度的評估方法可綜合考慮橋梁運營過程中的多種狀況，是在役橋梁服役性能評估的重要研究方向。目前，已有相關學者基于健康監測數據對橋梁服役狀態進行了可靠度評估。Li等[7]采用濾波泊松過程描述車輛荷載引起的吊索隨機索力響應，將一階可靠性方法用于在設計基準期內橋梁在極端交通荷載分布下的安全性評估。高欣等[8]針對車輛荷載效應具有多峰分布的特點，提出了橋梁服役期內車輛荷載效應極值近似服從廣義極值分布。陽霞等[9]采用極值統計理論對橋梁剩余服役期內的主梁應變極值進行了估計，并計算了不同承載能力下主梁的可靠度指標。魯乃唯等[10]采用Rice公式對車輛荷載作用下主梁彎矩極值進行了外推。劉小玲等[11]基于南京長江三橋長期監測數據，提出了一種基于統計理論的主梁撓度安全評估與預警方法。周建庭等[12]進行了全橋實時有限元分析，提出了一種基于結構有限點實測位移響應的安全評估方法。樊學平等[13]針對控制監測點變形失效非線性相關的特點，采用主梁動態極值撓度，進行了大跨度橋梁主梁體系動態可靠性預測。Guo等[14]引入不確定方法對某混凝土梁長期撓度可靠度進行了量化評估。眾多研究成果表明，基于活載效應的長期監測數據可有效實現運營期橋梁服役性能的可靠度評估，然而目前研究多集中在結構承載能力的可靠度評估，對于正常使用極限狀態下的橋梁服役性能評估研究較少，且已有研究大多是利用應變、索力長期監測數據進行評估，對于精度更高、受環境干擾更小的主梁撓度監測數據利用較少。同時，以往研究實例以公路橋為主，對于載重高、服役環境惡劣的重載鐵路橋梁應用較少。

現將活載撓度超限作為主梁豎向剛度不足的失效模型，采用串聯模型描述各截面活載撓度失效模式之間的關系，并基于健康監測系統實測撓度數據對運營期重載鐵路連續剛構橋活載撓度可靠度進行評估，為運營期重載鐵路橋梁服役性能評估提供一種有效方法。

1 活載撓度極值概率模型建立

活載撓度極值X1,X2,…,Xn可看作獨立同分布的隨機變量，u為活載撓度閾值，當Xi>u時，Xi即為超越樣本，該超越樣本的概率分布函數Fu(x)可表示為

Fu(x)=P(X≤x|X>u)

(1)

當閾值u足夠大時，超越樣本Xi可被廣義帕累托分布(generalized Pareto distribution，GPD)近似表達，則超越樣本Xi的概率分布函數Fu(x,u,σ,ε)可表示為

Fu(x,u,σ,ε)=1-[1+ε(x-u)/σ]-1/ε

(2)

式(2)中：x≥u；1+ε(x-u)/σ>0；u為閾值；σ為尺度參數；ε為形狀參數。

當活載撓度超越樣本的概率模型為GPD時，其活載撓度極值的概率分布函數為廣義極值分布(generalized extreme value distribution，GEVD)[10-11]，表達式為

(3)

λn為服役期內超越樣本發生的概率，計算公式為

λn=λ[1-Fu(x,u,σ,ε)]

(4)

式(4)中：λ為荷載效應發生概率。

2 基于串聯模型的可靠性指標

活載撓度是反映橋梁健康狀況的重要參數。一般而言，橋梁主梁上往往布置有多個撓度監測截面，各截面活載撓度的極限狀態方程gi表達式為

gi=Ri-Li=0

(5)

式(5)中：Ri為截面i的撓度限值；Li為截面i實測的活載撓度極值，i=1,2,…,m，m為撓度監測截面數。

各截面活載撓度的可靠度指標βi，計算公式為

βi=Φ-1(1-Pfi)

(6)

式(6)中：Φ-1為標準正態分布的逆概率分布函數，Pfi為截面i活載撓度超限概率。

Pfi計算公式為

(7)

式(7)中：FSmax,i為截面i的活載撓度極值概率分布函數；S0,i為截面i的撓度限值。

采用串聯模型描述各截面活載撓度失效模式之間的關系，即當m個撓度監測截面中，任一截面活載撓度超出限制，則代表體系失效。

根據式(6)，橋梁活載撓度可靠度指標的上界和下界計算公式為

βH=Φ-1(1-Pf,H)

(8)

βL=Φ-1(1-Pf,L)

(9)

式中：Pf,H和Pf,L分別為體系失效概率的上界和下界。

Pf,H和Pf,L分別可表示為

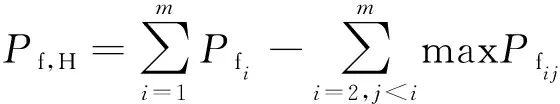
(10)

(11)

式中：Pfi為將各個截面失效概率按照從大到小排列，排序第i的截面失效概率，可定義為模式i失效概率，即模式1失效概率最高，模式m失效概率最低；Pfij為模式i和模式j的聯合失效概率。截面失效概率為該截面撓度極值超出撓度限值的概率，可根據式(7)計算。

模式i和模式j的聯合失效概率Pfij計算公式為

(12)

式(12)中：βi為模式i的可靠度指標；βj為模式j的可靠度指標；ρij為模式i可靠度指標與模式j可靠度指標的相關系數。

ρij計算公式為

(13)

式(13)中：E為數學期望。

3 工程應用案例

3.1 工程概況

某重載鐵路預應力混凝土連續剛構橋，跨徑布置為96 m+132 m+96 m。為實時監測運營期主梁豎向撓度，該橋布置有基于連通管原理的主梁撓度監測系統，撓度測點布置S1、S2、S3、S4、S5如圖1所示。

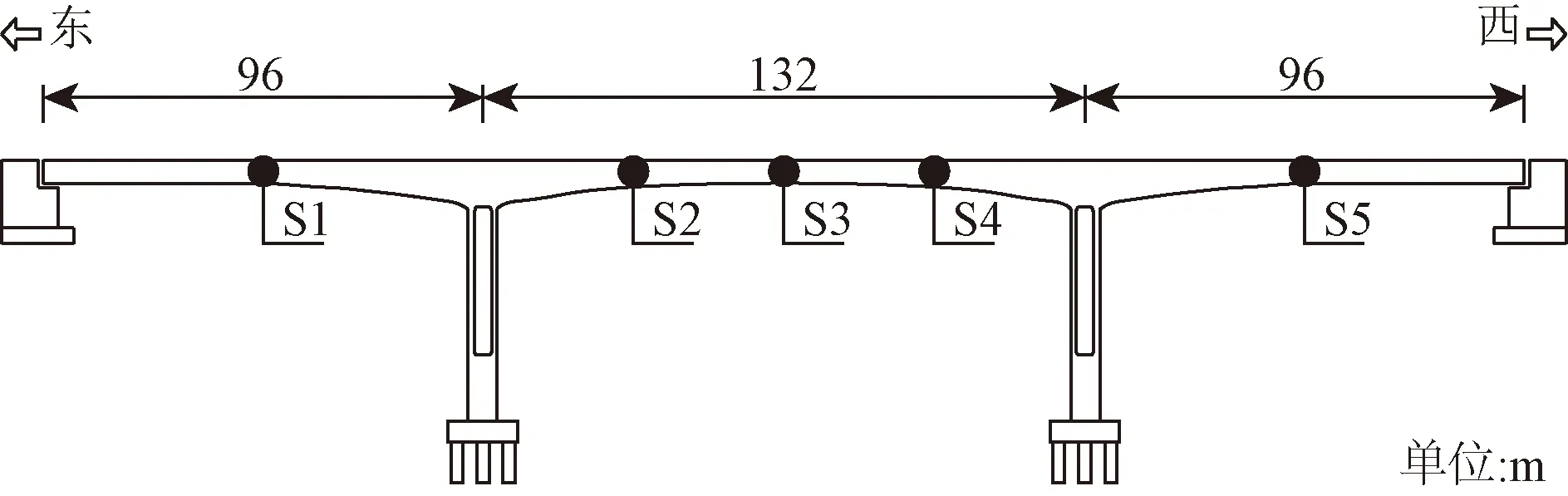
圖1 主梁撓度測點布置圖Fig.1 Measuring point positions of main girder deflection

3.2 活載撓度提取

2021年5月6號主跨跨中豎向撓度和環境溫度典型監測結果如圖2、圖3所示。主梁撓度由趨勢項和“突刺”組成，趨勢項是由于環境溫度變化引起，“突刺”則是由于列車過橋引起的活載撓度。

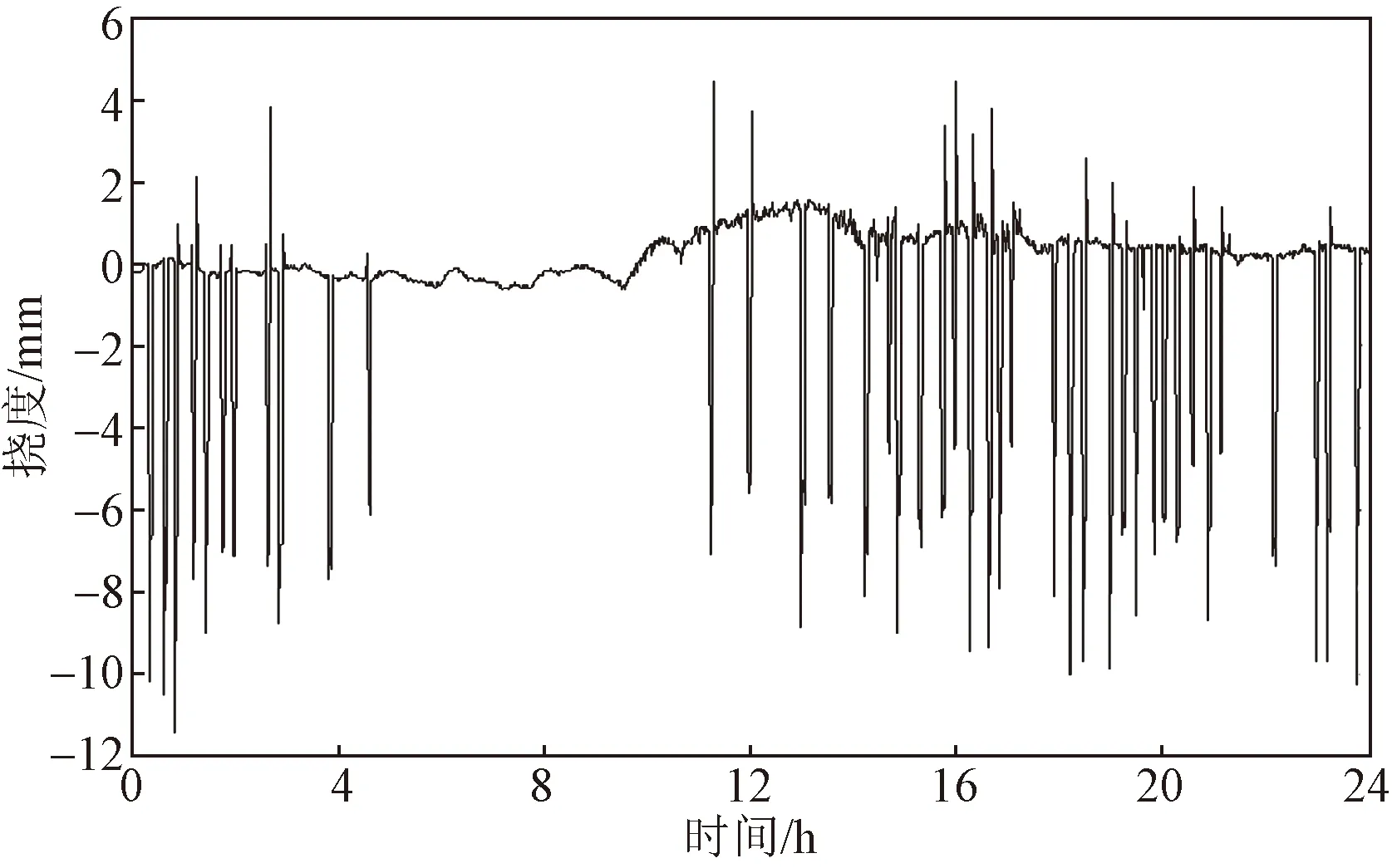
圖2 主梁跨中豎向撓度日典型監測結果Fig.2 Monitoring results of vertical deflections at the middle of main span on a typical day

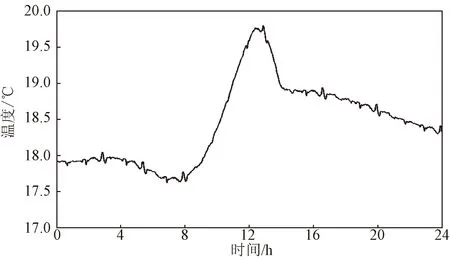
圖3 環境溫度日典型監測結果Fig.3 Monitoring results of ambient temperature on a typical day

采用小波變換[6]將主梁撓度中溫度變化引起的趨勢項去除，提取活載撓度。主梁溫度撓度及與環境溫度的相關性如圖4、圖5所示。圖5中，K為擬合直線的斜率，R2為擬合直線的確定系數。K值反映了撓度對溫度變化的敏感性，K值越大，撓度受溫度變化的影響越大。主梁活載撓度日典型監測結果如圖6所示。

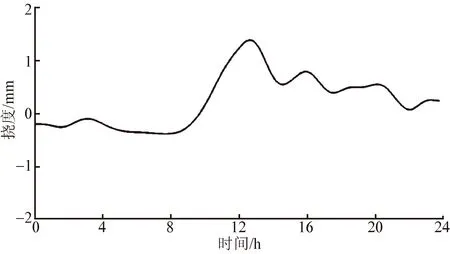
圖4 主梁溫度撓度日典型監測結果Fig.4 Monitoring results of temperature-induced deflections at the middle of main span on a typical day

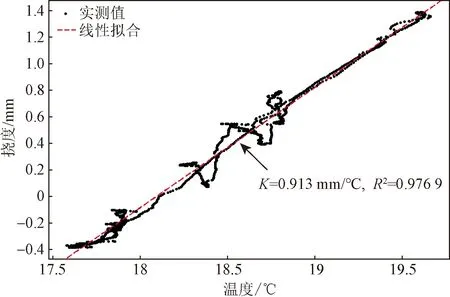
圖5 主梁溫度撓度與環境溫度的相關性Fig.5 Correlation between temperature-induced deflections and ambient temperature

圖6 主梁活載撓度日典型監測結果Fig.6 Monitoring results of vehicle-induced deflections at the middle of main span on a typical day

由圖6可知，上午5：00—11：00時間段，橋面無列車通過，其余時時間段，列車荷載分布具有明顯的隨機性。重載列車通過時，主跨跨中撓度均在12 mm以內。

3.3 活載撓度極值分布模型

采用剩余壽命圖法[15]確定活載撓度極值超樣本概率分布函數Fu(x,u,σ,ε)中的閾值u，尺度參數σ，形狀參數ε可通過最大似然法確定。

根據剩余壽命圖法，當平均超出函數e(u)近似線性變化時，即為合理閾值。平均超出函數e(u)計算公式為

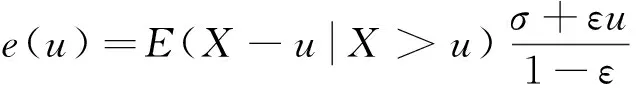
(14)

各截面活載撓度極值超樣本概率分布模型Fu(x,u,σ,ε)中各參數如表1所示。

表1 活載撓度極值超樣本概率分布模型參數Table 1 Parameters of probability model for extreme deflection of exceed threshold value

假定橋梁的服役年限T為100年，根據式(4)，計算服役期內超越樣本發生的概率λn，將超越樣本發生概率λn、閾值u、尺度參數σ、形狀參數ε代入式(3)，即可建立活載撓度極值概率分布模型FSmax(S)。各截面活載撓度極值概率分布函數FSmax(S)中各參數如表2所示。

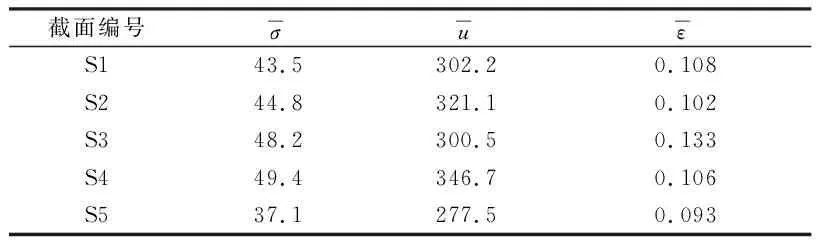
表2 活載撓度極值概率分布模型參數Table 2 Parameters of probability model for extreme deflection

3.4 各截面活載撓度可靠度評估結果

根據現行《鐵路橋梁檢定規范》(鐵運函〔2004〕120號)要求，設置撓度限值分別L/1 800(L為跨度)，對活載撓度可靠性進行評估，以實現正常使用極限狀態下的主梁豎向剛度評估。

根據活載撓度極值概率分布模型參數，建立各截面活載撓度極值概率分布，從而得到各截面活載撓度超限概率，將活載撓度超限概率代入式(6)，得到各截面活載撓度可靠度指標。

橋梁服役時間為100年時，各截面活載撓度可靠度指標如圖7所示。

由圖7可知，各截面活載撓度可靠度指標總體呈對稱分布，但由于各截面活載撓度極值分布存在差異，主梁對稱截面活載撓度可靠度指標也略有差異。由于主跨跨中截面撓度受重載列車影響較大，主梁跨中截面活載撓度可靠度指標最小，為4.32。

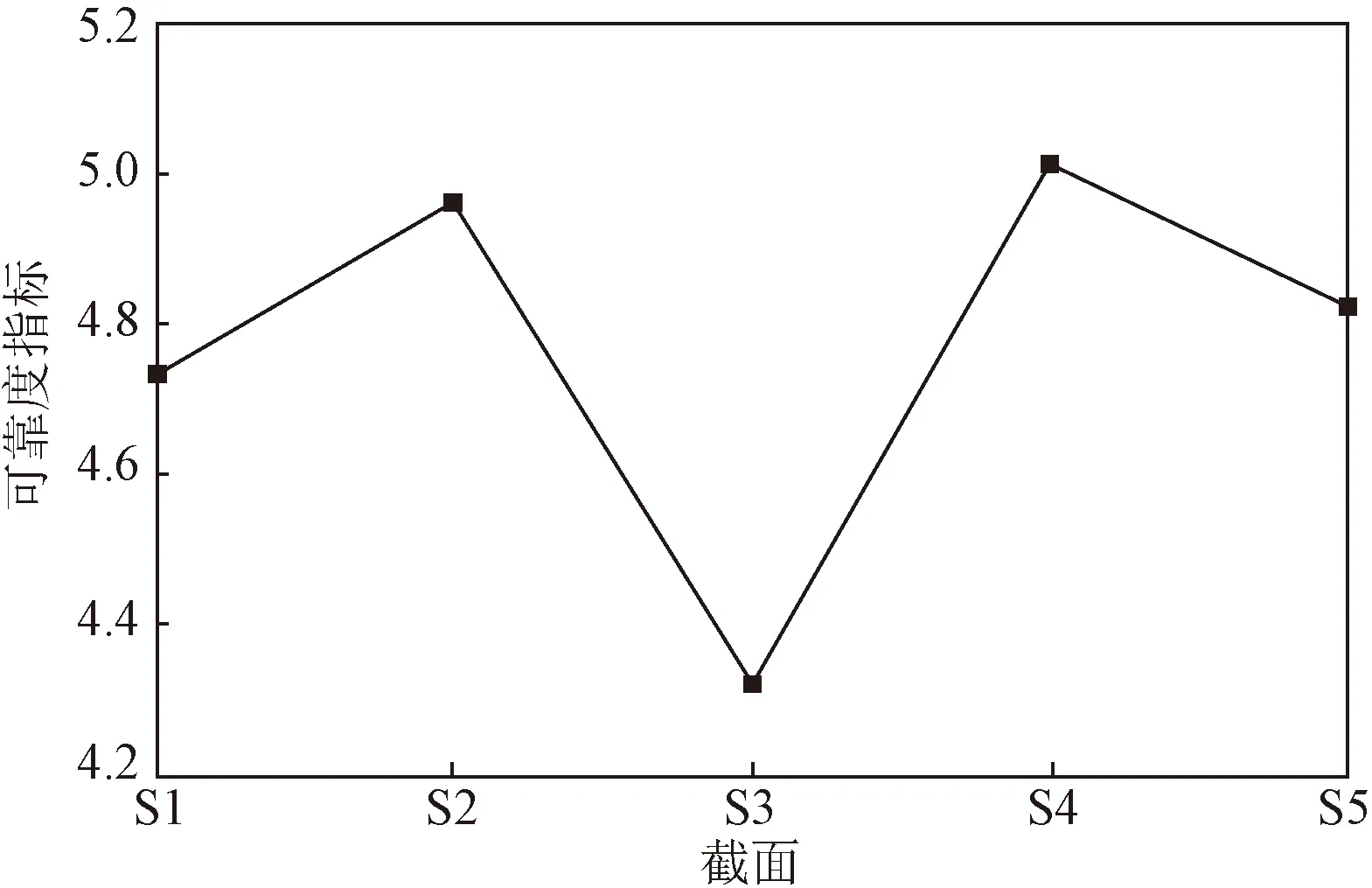
圖7 主梁各截面活載撓度可靠度指標Fig.7 Vehicle-induced deflection reliability of girder sections

各截面活載撓度可靠度指標隨服役時間的變化規律，如圖8所示。

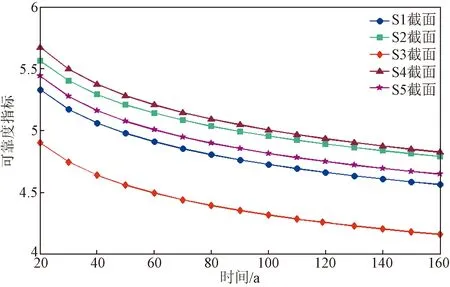
圖8 活載撓度可靠度指標隨服役時間的變化規律Fig.8 Change of reliability indices of vehicle-induced deflection vs service time

由圖8可知，各截面活載撓度可靠度指標在服役初期下降較快，隨著服役時間的增加，可靠度指標下降速率趨于穩定，即使橋梁服役時間達到160年，各截面活載撓度可靠度指標仍達到4.16以上。

3.5 橋梁體系活載可靠度評估結果

根據式(13)計算不同截面活載撓度可靠度指標間的相關系數ρij，如圖9所示。

圖9 各截面活載撓度可靠度指標間的相關系數Fig.9 Correlation coefficient of vehicle-induced deflection reliability with different sections

將ρij代入式(12)，根據式(8)～式(11)，計算得到橋梁活載撓度可靠指標的上界和下界。該橋于2020年5月采用體外索對主梁進了加固，加固前后橋梁體系活載撓度可靠指標上界及下界隨服役時間的變化如圖10所示。

由圖10可知，橋梁體系活載撓度可靠度指標下界和上界接近，橋梁體系活載撓度可靠度指標隨服役時間的變化與主跨跨中截面十分相似，表明主跨跨中是主梁活載撓度可靠性的控制截面。橋梁經過體外索加固后，主梁剛度增加，體系活載撓度可靠度指標上升。相比加固前，服役時間為100年時，可靠度指標上界和下界分別上升了5.21%、5.23%。

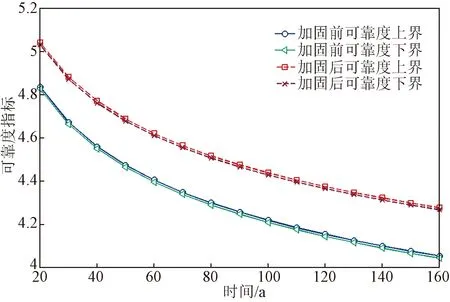
圖10 橋梁體系可靠度指標隨服役時間的變化規律Fig.10 Change of bridges system reliability with service time

目標可靠度指標為2.5[16]。橋梁經加固后，服役時間為160年時，橋梁體系活載撓度可靠度指標βH≈βL=4.3，大于目標可靠度指標。

4 結論

將主梁活載撓度超限作為豎向剛度不足的失效模型，采用串聯模型描述各截面活載撓度失效模式之間的關系，并基于健康監測系統實測數據對重載鐵路連續剛構橋運營期活載撓度可靠度進行評估，有以下結論。

(1)活載撓度超限可作為主梁豎向剛度不足的失效模型，串聯模型綜合了主梁各監測截面撓度數據，可有效反映各截面活載撓度失效模式之間的關系。

(2)主梁各截面活載撓度可靠度指標總體呈對稱分布。由于主跨跨中截面撓度受重載列車影響較大，主跨跨中截面活載撓度可靠度指標最小，為主梁活載撓度可靠性的控制截面。活載撓度可靠度指標在服役初期下降較快，隨著服役時間的增加，可靠度指標下降速率趨于穩定。

(3)橋梁經過體外索加固后，主梁剛度增加，活載撓度可靠度指標上升。相比加固前，服役時間為100年時，橋梁活載撓度可靠度指標上界和下界分別上升了5.21%、5.23%。橋梁服役時間為150年時，橋梁活載撓度可靠度指標近似為4.3，大于目標可靠度指標。