指數形式的二次相關GCC-PHAT-β時延估計算法

李皖婷， 李登峰， 張修靖， 張天婷， 黃杉杉

(長安大學電子與控制工程學院， 西安 710064)

聲源定位是以時延值已知與聲速已知作為前提條件，以時間與速度的關系式計算聲源到不同聲傳感器之間的距離[1]，通過多元十字陣列計算得到目標聲源的俯仰角、方位角和距離等位置信息[2]。由于多元十字陣列的幾何特性，在對聲源進行定位的過程中時延值估計的誤差被放大，使定位誤差也隨之增大[3]。因此如何降低在時延估計過程中的誤差對提高聲源定位的準確度具有重要意義。

在對時延值進行估計時，前期普遍使用的基本互相關算法具有峰值不凸出導致時延估計誤差較大等明顯的缺陷；為了彌補互相關算法的不足，前人在原有算法的基礎上引入了加權函數的概念后得到了廣義互相關算法，文獻[4]在相位變換(phrase transform，PHAT)加權函數的廣義互相關算法的基礎上，將算法的加權函數與相關噪聲的互功率譜相減，再根據信噪比的不同賦予其不同的權值，并添加一個相干函數來構造一種新的加權函數的時延估計算法，該算法在信噪比為0 dB以上時能有效地抑制噪聲而凸出峰值, 降低了時延值在估計過程中的誤差，但并沒有對信噪比在0 dB以下時的峰值凸出情況進行說明；文獻[5]基于廣義平滑相干變換(smooth coherent transform，SCOT)算法和廣義HB算法，提出了一種SCOT-HB復合加權廣義互相關算法，在加權函數的分子項中加入模平方相干函數來提高信號中高信噪比部分的能量并抑制低信噪比部分的能量，在信噪比不高于0 dB時減少了時延估計過程中的計算量，而且提升了時延估計的穩定性和正確率，但該算法并沒有對0 dB以下時的峰值凸出和時延估計情況進行解釋說明；文獻[6]將最小平均P范數與加權函數相結合，提出了一種基于最小平均P范數的時延估計算法，該算法在非高斯環境下具有能有效抑制諧波、收斂性強、時延估計精度高和迭代速度快等優點，但當其受到的噪聲信號強度大于語音信號強度時該算法的時延估計精度降低。文獻[7] 基于高階累積量和二次相關算法，提出了一種結合希爾伯特變換方法的時延估計算法，該算法使得峰值更加凸出，均方根誤差更低且能獲得更高的時延估計精度，但在2 dB以下的信噪比時算法失效。

針對上述問題，現提出一種應用在低信噪比條件下的指數形式的廣義二次相關算法。首先，以已有廣義二次相關算法為基礎，將獲得的功率譜函數進行傅里葉逆變換后，對結果進行指數運算,得到改進算法；然后在由軟件構造的加有高斯白噪聲的兩路單頻正弦波信號，分別在不同信噪比下對廣義互相關算法、廣義二次相關算法和改進算法進行實驗仿真，驗證在低信噪比下峰值較凸出的時延估計算法；最后選用一段男聲音頻作為信號源，比較3種算法在進行時延估計時所產生的誤差大小，獲得在-10～10 dB低信噪比范圍內的較優算法。

1 時延估計算法

1.1 基本互相關時延估計算法

設聲傳感器M1和M2接收到的信號分別為x1(t)和x2(t)，假定噪聲n1(t)與n2(t)為互不相關的高斯白噪聲，且噪聲和聲源信號s(t)之間也互不相關，表達式為

x1(t)=α1s(t-τ1)+n1(t)

(1)

x2(t)=α2s(t-τ2)+n2(t)

(2)

式中：α1和α2分別為聲源s(t)傳播到M1和M2后的衰減系數；τ1和τ2分別為聲源s(t)到達聲傳感器M1和M2所需要的時間。則以τ=τ1-τ2來表達聲傳感器M1和M2接收到聲源信號的時間差，即為時延值。兩路信號x1(t)、x2(t)的互相關函數R12(τ)可表示為

R12(τ)=E[x1(t)x2(t-τ)]

(3)

將式(1)、式(2)代入式(3)，可得

R12(τ)=α1α2E[s(t-τ1)s(t-τ2-τ)]+

α1E[s(t-τ1)n2(t-τ)]+

α2E[n1(t)s(t-τ2-τ)]+

E[n1(t)n2(t-τ)]

(4)

由于假定高斯白噪聲n1(t)、n2(t)互不相關，且噪聲n1(t)、n2(t)和聲源信號s(t)也互不相關，因此式(4)可表達為

R12(τ)=α1α2E[s(t-τ1)s(t-τ2-τ)]

=α1α2Rss[τ-(τ1-τ2)]

(5)

由自相關函數的性質可知：當τ-(τ1-τ2)=0，即τ=τ1-τ2時，R12(τ)值取最大[8]。因此信號x1(t)和x2(t)之間的時延可表示為

(6)

由上述可知，時延可由目標聲源到達兩個聲傳感器之間信號所構成的互相關函數來獲得[9]。是以要獲得準確的時延值，就必須準確求解出互相關函數的最大值，這就要使其最大峰值十分凸出，但是在互相關函數的計算中，以兩個高斯白噪聲互不相關和高斯白噪聲與聲源互不相關為前提條件，該結論才會順利得出。然而現實環境中充斥著大量噪聲，假設難以實現，所以由基本互相關時延估計算法得到的函數圖形中，其峰值最大處并不凸出，因此準確計算出時延值極其艱難。

1.2 GCC-PHAT-β時延估計算法

廣義互相關(generalized cross-correlation phrase transformation-β，GCC-PHAT-β)算法[5]是對基本互相關算法加以改進而得到的算法，將加權函數乘以由兩路信號進行傅里葉變換得到功率譜函數[1]，使其達到增強抗噪性能的目的并使對時延進行估計時的誤差降低。

設聲傳感器M1和M2接收到的信號分別為x1(t)和x2(t)，假定噪聲n1(t)與n2(t)為互不相關的高斯白噪聲，且噪聲和聲源信號之間也互不相關。

x1(t)=α1s(t)+n1(t)

(7)

x2(t)=α2s(t-τ)+n2(t)

(8)

式中：τ為聲源到達聲傳感器M1、M2之間的時延。則兩路信號x1(t)、x2(t)所構成的Rx1x2(τ)為

(9)

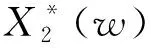
將函數Rx1x2(τ)經傅里葉逆變換從頻域轉換到時域，檢測最大峰值并對其進行時延估計。其算法的原理圖如圖1所示。選取的加權函數各有差異，算法的公式組成也各有不同，如表1所示。在現實應用中，加權函數的選取還需隨著具體應用場景的改變而改變[10]，使傅里葉逆變換后的函數最大峰值更為凸出，以便得到高精度的時延值。

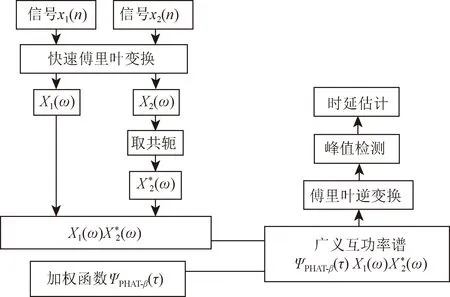
圖1 廣義互相關算法原理圖Fig.1 Schematic diagram of generalized cross-correlation algorithm

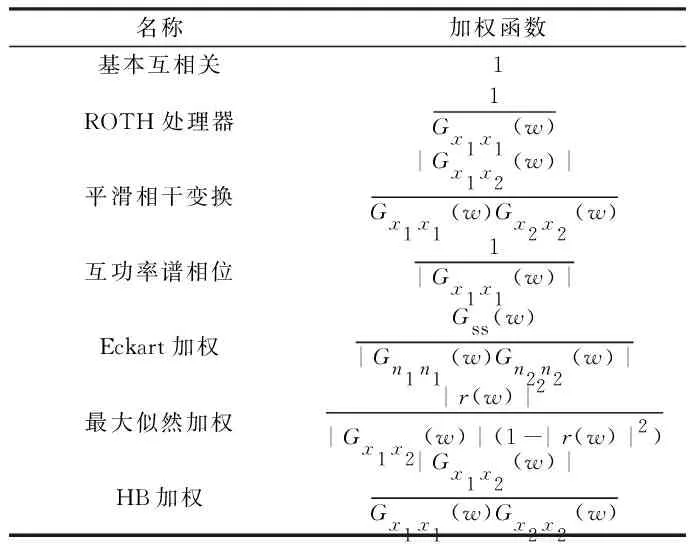
表1 常用的幾種加權函數Table 1 Several commonly used weighting functions

|r(w)|2表達式為

(10)

當處在信噪比較低的環境中或對多個目標聲源進行定位時，噪聲與聲源之間疊加或多個聲源疊加產生的問題嚴重影響著GCC-PHAT-β算法進行時延估計時的性能；反之當處在信噪比較低的環境中并對單個目標聲源進行定位時，GCC-PHAT-β算法和基本互相關算法相比易達成且時延估計造成的誤差較低[5]。總而言之，在較低信噪比的環境中，GCC-PHAT-β算法對單個目標聲源進行定位時的性能方面和誤差方面都強于基本互相關算法。

1.3 改進的二次相關GCC-PHAT-β時延估計算法

1.3.1 二次相關時延估計算法

為了增強基本互相關算法在進行時延估計時的抗噪性能，在其基礎上進行完善后取得二次相關算法來有效降低時延估計過程中信噪比下降時噪聲占據比例較大對時延估計性能的影響。

x1(t)的自相關函數為

R11(τ)=E[x1(t)x1(t-τ)]

=α1α1Rss+α1Rsn1+α1Rn1s+Rn1n1

(11)

x1(t)和x2(t)的互相關函數為

R12(τ)=E[x1(t)x2(t-τ)]

=α1α2Rss+α1Rsn2+α2Rsn1+Rn1n2

(12)

此時R11(τ)與R12(τ)仍是以時間τ為因變量的函數，對這兩個函數進行第二次互相關運算，取得二次相關函數RRR(τ)為

RRR(τ)=E[R11(τ)R12(t-τ)]

(13)

用式(11)、式(12)來表示式(13)，假定目標聲源信號與噪聲互不相關，則式(13)可表示為

RRR(τ)=RRS(τ-D)+RRN(τ)

(14)

式(14)中：RRS、RRN分別為聲源、噪聲的二次相關函數。假設噪聲之間互不相關，則RRN=0。從式(14)中可知，在τ=D時，RRS(τ-D)獲得最大值，即二次相關函數RRR(τ)獲得最大值，則此時的τ就為所求的時延值。而在使用二次相關算法對時延值進行估計時，增加了先對一個聲傳感器接收到的聲音信號施行自相關運算的步驟，以便增強算法的抗噪性能[11]。因此二次相關運算與GCC-PHAT-β算法在信噪比逐漸降低的條件下，二次相關算法更能進行有效的時延估計，其原理框圖如圖2所示。

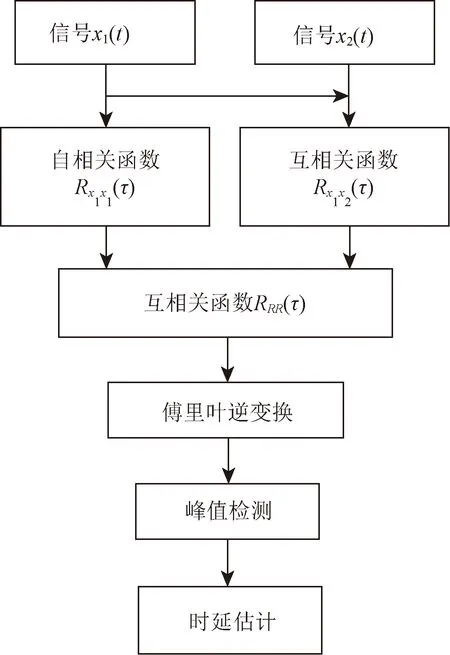
圖2 二次相關算法流程圖Fig.2 Quadratic correlation algorithm flowchart

1.3.2 二次相關GCC-PHAT-β時延估計算法

GCC-PHAT-β算法是將加權函數乘以由兩路信號進行傅里葉變換得到功率譜函數，使其算法的抗噪性能得到加強，并使對時延進行估計時的誤差降低，是時延估計領域里比較典型的算法。但是算法的抗噪性能隨著信噪比的逐漸降低而大幅度減弱，對時延值進行估計時準確率下降而誤差變大。而在使用二次相關算法對時延值進行估計時，增加了最開始就對一路聲音信號施行自相關運算的步驟，以便增強算法的抗噪性能。為了增強二次相關算法在對時延值進行估計過程中的精度，因此將其與加權函數相結合得到二次相關GCC-PHAT-β算法，達到降低時延估計誤差和提高算法抗干擾能力的目的。

二次相關GCC-PHAT-β算法[12]起初先對時域信號x1(t)進行自相關運算，同時對時域信號x1(t)、x2(t)進行第一次互相關運算，對分步獲得的兩個函數進行第二次的互相關運算，二次相關函數RRR(τ)由此取得，然后將其與加權函數ψPHAT-β相乘得到功率譜函數GR11R12(w)，檢測經傅里葉逆變換后的功率譜函數所獲得的函數峰值最大處，計算時延值。其原理框圖如圖3所示。

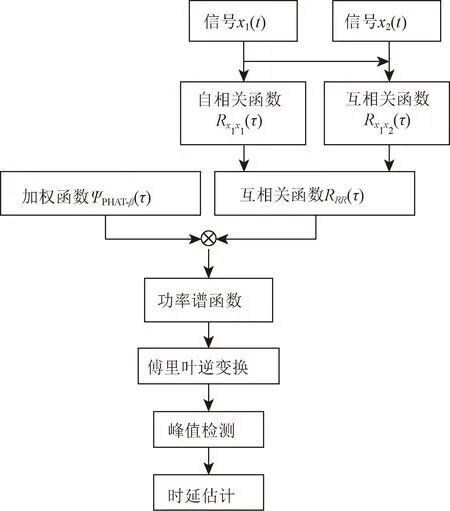
圖3 廣義二次相關算法原理框圖Fig.3 Principle block diagram of generalized quadratic correlation algorithm

1.3.3 指數形式的二次相關GCC-PHAT-β時延估計算法

為了解決二次相關運算在信噪比降低時使得噪聲強度增加，使其對時延估計的誤差變大這種問題[13]，提出在二次相關算法的基礎上,再乘以加權函數ψPHAT-β,對其得到的功率譜函數進行傅里葉逆變換，對其做指數運算并檢測指數運算后函數的最大峰值處,從而計算出時延值。改進算法的原理框圖如圖4所示。

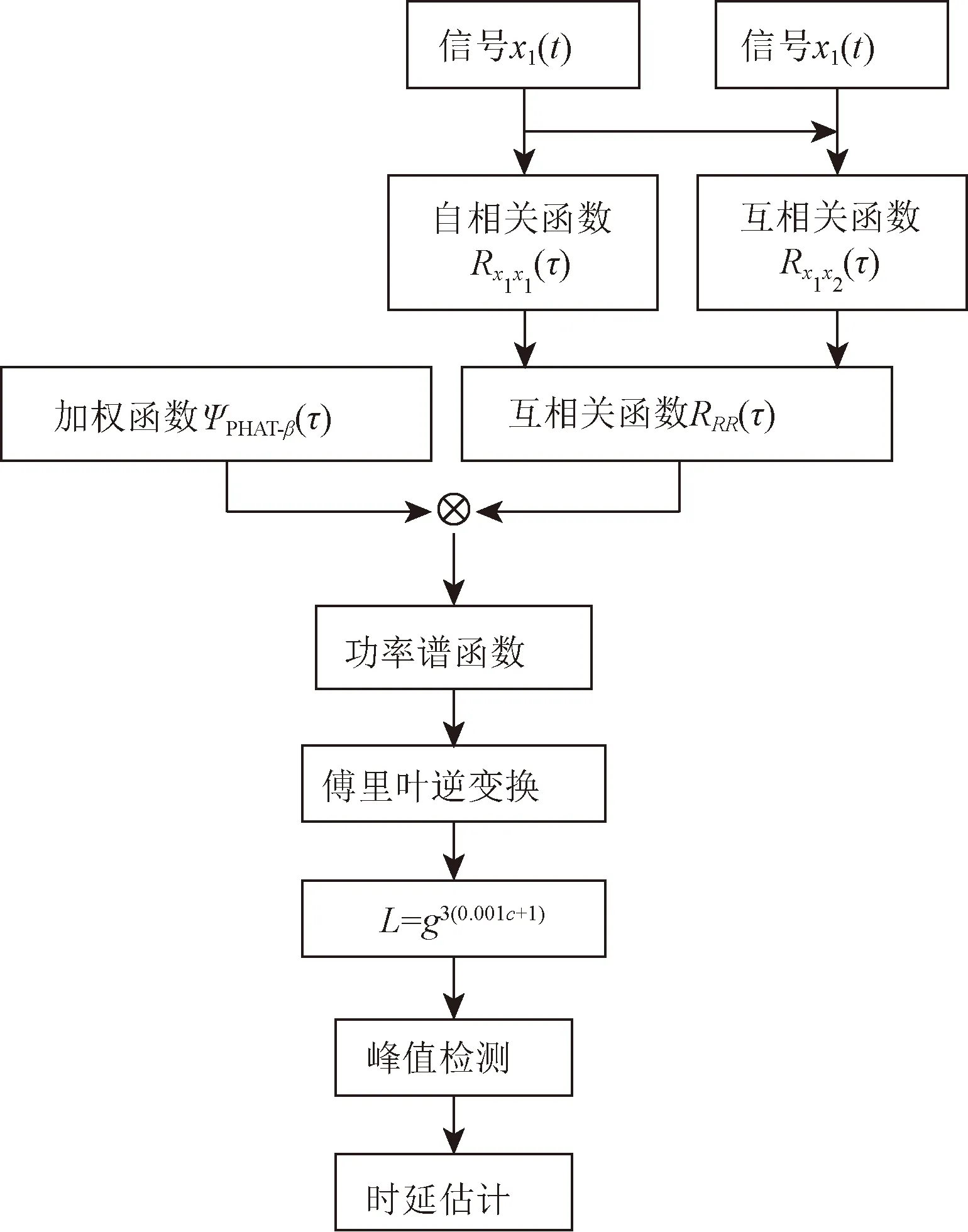
L為傅里葉逆變換指數運算結果；g為傅里葉逆變換后的相關函數圖4 改進算法原理框圖Fig.4 The schematic diagram of the improved algorithm

2 仿真研究

為了對改進算法的時延估計性能進行驗證，利用軟件MATLAB[14]構造了兩路單頻正弦波信號，信號頻率為1 000 Hz、幅值為5。兩路信號之間延時1.6 ms,并在其中分別加入高斯白噪聲，采樣頻率50 kHz，采樣點數1 024。在信噪比分別為-10、-5、0、5、10 dB的環境下，將GCC-PHAT-β算法、二次相關GCC-PHAT-β算法[12]以及指數運算形式的二次相關GCC-PHAT-β算法進行實驗仿真，仿真結果如圖5所示。

由圖5(a)、圖5(b)、圖5(c)可得出，信噪比包含5 dB及以上時，GCC-PHAT-β算法、二次相關GCC-PHAT-β算法和本文改進算法均能夠使函數的相關峰值銳化，但其銳化程度不同，相較于其他兩種算法，雖然都能將峰值較為準確地估計出來，但本文改進算法中兩路信號相關函數的最大峰值非常尖銳，信號峰值遠高于旁瓣，該改進算法在信噪比0 dB以上時延估計性能遠優于其他算法。

對比圖5(d)、圖5(e)可得，當信噪比小于0 dB時，GCC-PHAT-β算法獲得的最大峰值幾乎與噪聲等高，系統難以準確判斷時延值是最大峰值對應的時間值所得還是噪聲所得，時延估計誤差顯著增大，二次相關GCC-PHAT-β算法亦獲取不到較為凸出的峰值最大處，然而在本文改進算法中卻相當凸出，遠高于旁瓣。因此信噪比較低時，使用改進算法進行時延估計時可得到更為精準的時延值，對噪聲有較強的抗干擾能力。

圖5 不同信噪比下的仿真結果圖Fig.5 Simulation results under different SNR

利用軟件MATLAB對GCC-PHAT-β算法、二次相關GCC-PHAT-β算法和指數形式的二次相關GCC-PHAT-β算法在對時延值進行估計時產生的誤差進行實驗，進一步檢驗其對時延進行估計時的性能。實驗所需信號源選用男聲音頻，頻帶范圍為50～1 000 Hz，截取其中4 096個數據點，兩路信號的時間延遲10個數據點，比較3種算法在進行時延估計時所產生的誤差大小，確定-10～10 dB范圍內的最優算法。

由圖6可知，3種算法對時延值進行估計時所產生的誤差隨著逐漸降低的信噪比而漸漸增大。在0～10 dB時，3種算法進行時間延遲估計的誤差無甚差別，都將接近于0;在-10～0 dB時, GCC-PHAT-β算法、二次相關GCC-PHAT-β算法的時延估計誤差會隨著信噪比的降低而變大,而改進算法的時延估計誤差變化較為平緩,誤差值在0～0.1范圍內波動，時延估計性能在信噪比較低時依舊良好。以上結果表明,在對時延值進行估計時，指數形式的二次相關GCC-PHAT-β算法的性能在信噪比較低時優于其他兩種算法。

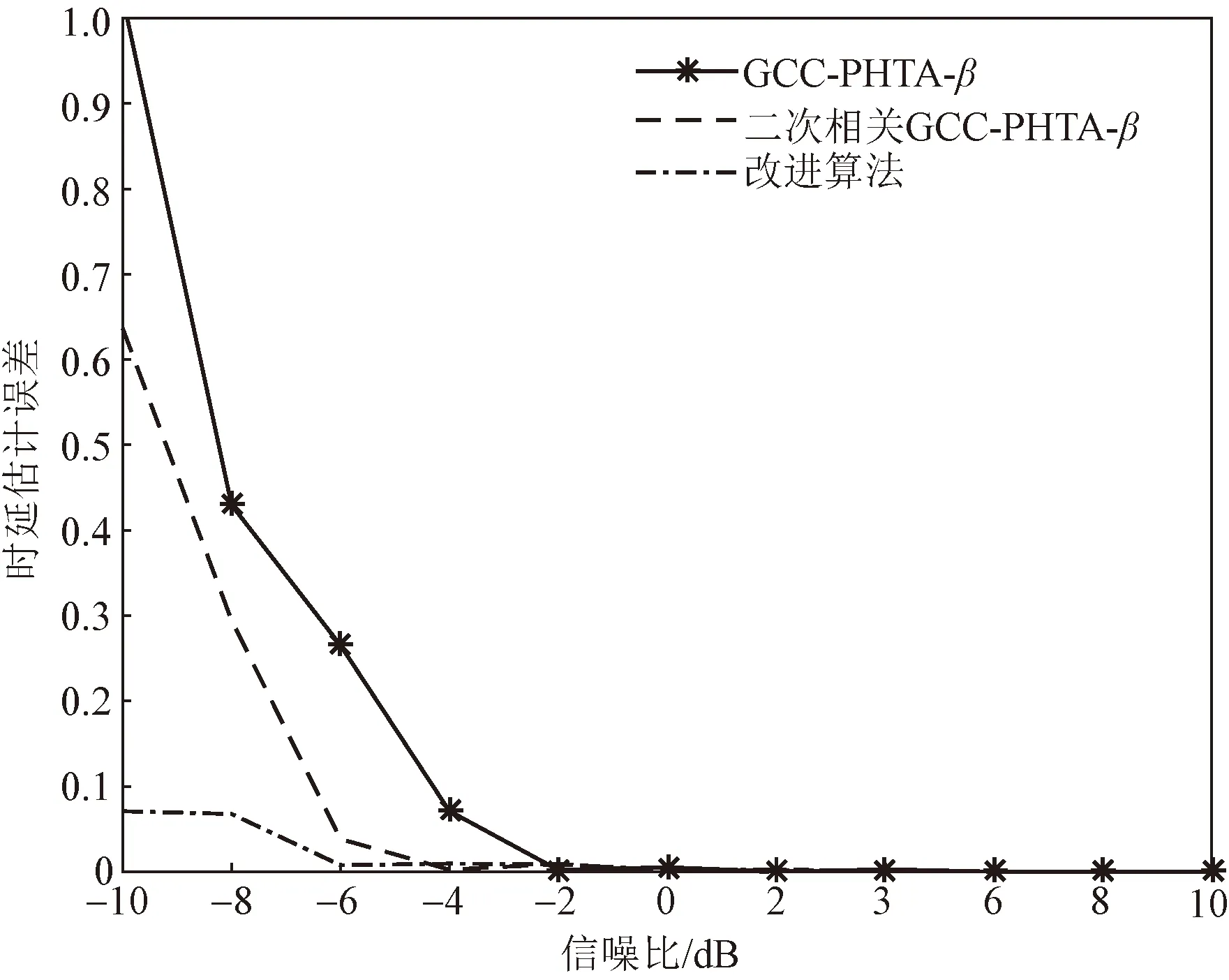
圖6 三種算法的時延估計誤差Fig.6 Delay estimation errors of three algorithms

3 結論

針對在低信噪比的情況下，GCC-PHAT-β算法和二次相關GCC-PHAT-β算法性能較差和時延估計誤差變大的問題，討論了一種對二次相關GCC-PHAT-β算法中功率譜函數進行傅里葉逆變換后再進行指數運算的改進算法,得出如下結論。

(1)進行指數運算的改進二次相關GCC-PHAT-β算法所獲得的最大峰值更為尖銳凸出，使降低時間延遲誤差的目標得以實現。

(2)在-10～10 dB的信噪比范圍內，指數形式的二次相關GCC-PHAT-β算法的時延誤差顯著低于另外兩種算法;在低于-10 dB內,改進算法仍具備一定優勢。

總而言之，相對于GCC-PHAT-β算法和二次相關GCC-PHAT-β算法，改進算法在信噪比較低時的抗噪性能明顯增強，時延估計誤差顯著下降。