關于第54屆國際化學奧林匹克試題4-9的表觀解離常數計算的討論

張思翰，梁馳予，邱曉航

南開大學化學學院，天津 300071

鋰離子電池的研究與應用已經對人們的生活產生了深遠的影響。2019年諾貝爾化學獎便授予了John B. Goodenough，M.stanley Whittlingham以及Akira Yoshino三人，以表彰他們在鋰離子電池發展方面做出的巨大貢獻。傳統的鋰離子電池受到能量密度以及原料資源儲量等方面的限制，難以滿足現階段大規模儲能需求。新型的鋰硫電池由于具有遠高于商業鋰電池的比容量(～1675 mAh·g-1，商用鈷酸鋰電池～150 mAh·g-1)，以及低污染、環境友好等優勢，具有極大的應用潛力[1,2]。

“穿梭效應”是限制鋰硫電池發展的一個關鍵問題[3]。電池正極放電過程常伴隨多硫化物的生成以及溶劑化，溶劑合多硫化物遷移至電池負極區與負極片直接反應，將導致電池容量不可逆地衰減。因此，研究多硫化物在常見的鋰離子電解液中的溶劑化行為對鋰硫電池的設計具有重要意義，2022年IChO筆試第4題便以此為背景設題，其中第4-9小題涉及了多構象化合物的平衡計算問題。閱卷、仲裁過程中發現，有許多同學由于對化學熱力學概念理解不充分而失分。

1 題目與答案

4-9中[4]，由于聚硫化物在DME中第二步解離常數極小(Kd1/Kd2≈ 1014)，因此溶液中多硫化物主要以Li2S6(DME)以及其一級解離形式存在，可以將原平衡簡化為如圖1所示模型：

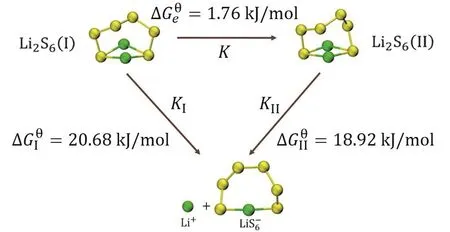
圖1 簡化的聚硫化物溶劑合平衡模型

最常見的錯誤解答(2)采用了與上式類似的方法計算，這種方法簡單地將化合物Li2S6(DME)的吉布斯自由能視為兩個構象吉布斯自由能的加權平均，再利用圖中關系算出總解離反應自由能變，既而計算表觀解離反應自由能變如下：

試題所參考論文中給出的表觀解離常數如下[5]：

根據熱力學基本原理[6]，正確的解題方法是，將體系視為多重平衡，利用平衡時各物種之間濃度關系，列出表觀平衡常數的表達式：

顯然，方程(3)與(2)不等價。

2 熱力學角度討論

2.1 化學勢推求

試題參考文獻[5]的作者列出方程(1)的思路是，將總反應看作兩個構象解離方程式按平衡時分配比例δI，δII的加和：

設構象I與構象II的總濃度為c，作者認為此時左側的化學勢表達式如下：

利用平衡時方程式左側化學勢等于右側化學勢的條件，能夠得到方程(1)。

但如果進行嚴格推導，列出上述反應的自由能變，式中各項化學勢可以根據van’t Hoff方程給出：

方程(10)結果與方程(3)等價，我們按照文獻作者的思路進行的嚴格的熱力學推導，卻得出了不同的結論。(4)式的表示方法默認了兩個構象按照一定的比例協同作用才可以解離。但是實際上，構象I與構象II的解離反應是獨立的，并不是協同過程，因此，平衡時Li2S6(I)、Li2S6(II)與解離產物的化學勢兩兩相等，如方程(11)。

這兩種計算方式反映了對總反應方程式中系數的不同理解：式(4)表示構象I與構象II按照摩爾比δI: δII協同解離，而正確的理解應是，反應有δI的概率按照構象I的方式解離，δII的概率按照構象II的方式解離。

2.2 熱力學過程圖

為了進一步明確錯誤成因，可以繪出兩個計算方法對應的熱力學過程圖，并給出其中每一過程的自由能變(圖2)。

圖2 仲裁過程中針對Q4-9所使用的解釋性熱力學狀態圖

對比可以發現，兩種計算方法間正好相差了混合自由能變項。方程(2)相當于按照圖2中路徑II求算反應的自由能變，而方程(3)相當于按照反應路徑I求算，兩種方法的本質差異在于，計算反應物自由能時，是否考慮了構象混合所產生的熵變。

體系自由能變化與不同狀態組成示意如圖3所示。

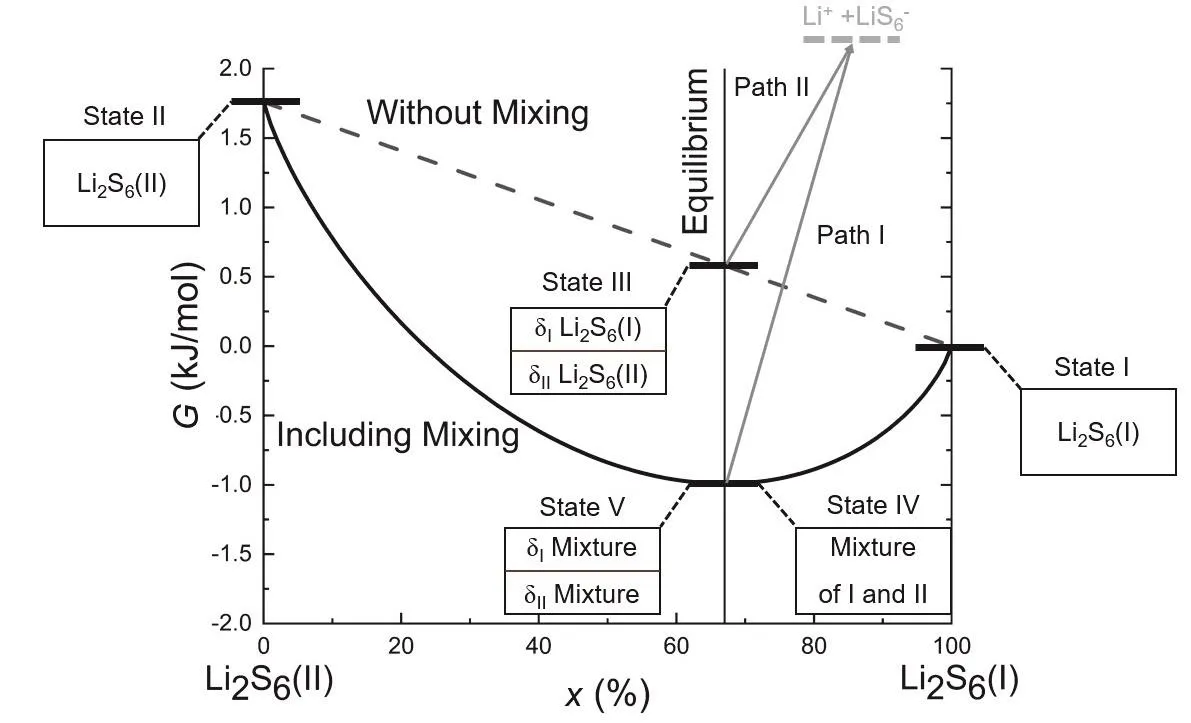
圖3 體系自由能變化與不同狀態組成示意圖

由于存在混合作用，圖3中自由能的最低點應是考慮了混合作用的自由能曲線與平衡組成比線的交點，對應狀態IV；若將兩構象自由能的加權平均值作為反應物自由能，其所處狀態為圖3中不考慮混合線與平衡線的交點，對應狀態III。

狀態III的自由能的大小處于兩個構象之間，具有向自由能較低構象轉變的趨勢，而這與兩構象具有轉化平衡、能夠共存這一事實相違背。簡單來說，狀態III其實是一個理想的非穩態，體系中存在一個假想的隔板，將構象I與構象II分隔開，并阻止了構象間的相互轉化。

從狀態III到狀態IV過程自由能變化可以選擇兩種途徑進行計算。假設狀態III中隔板兩側構象不發生轉化，抽開隔板，兩構象混合，此過程自由能變化可以使用混合自由能變公式求算：

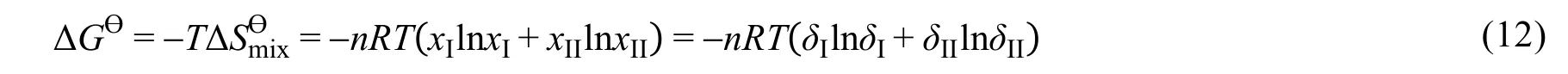
同樣，也可以保留隔板，使隔板兩邊均達到構象轉化平衡，算出由狀態III到狀態V間的構象轉化自由能變。狀態V至狀態IV間存在“吉布斯佯謬現象”，因為隔板兩側均達到構象轉化平衡后，隔板兩側構象不可區分，由于體系的量子效應，因此過程V→IV過程計算熵變需要添加校正項，校正后此過程自由能變為0。

在針對此題的討論過程中，錯誤理論的其中一種辯解思路便是將構象I與構象II認定為同一化合物，因此認為計算過程中存在“吉布斯佯謬”。判斷一個混合過程是否存在“吉布斯佯謬”首先需要明確這一佯謬出現的條件：混合前隔板兩側粒子具有完全一致的內稟性質，狀態III中，隔板兩側分別是純的構象I與純的構象II，兩構象之間有明確的單點能差異與空間結構差異，內稟性質不同。假使隔板兩側交換一個分子，顯然隔板兩側具有能量變化，其大小為一個分子在構象I與II之間轉換的能量差，這一過程存在著能量變化。通過以上兩點，可以發現狀態III的混個過程與出現“吉布斯佯謬”所需隔板兩側粒子完全一致這一前提相矛盾，因此這一辯論思路是錯誤的。

3 統計物理學角度討論

從上面的討論可以看出，兩種方法的差別來自于對多構象化合物熱力學計算的不同認識。由于討論的是平衡體系，不同系綜具有等效性，下面使用恒定(T，p，N)條件使用等溫等壓系綜，給出該體系的熱力學函數表達形式[7,8]，其中化學勢可由(13)式求得：

對于本題所涉體系，構象I與構象II之間可以通過振轉相互轉化，可以視為處于兩個不同能級上的粒子數滿足玻爾茲曼分布定律：

由此可算出總解離反應自由能變，可證方程(18)與(3)等價。方程(18)中包含了由于混合作用導致的自由能變。據此，還可以合理外推出多構象的化合物摩爾化學勢的計算方法：

4 總結討論

根據以上討論，我們可以發現導致方程(1)以及(2)錯誤的原因，是沒有對物理化學基礎理論與思想充分理解，并且主觀臆斷造成的。此外，清華大學張強教授于今年發表的一篇論文中，利用測定溶液電導率的方法對此體系的一級解離常數進行了實驗驗證[9]，計算結果與實驗結果對照如表1所示，實驗值與方程(3)計算結果吻合較好。

表1 不同方法取得結果對照

從試題角度出發，此題僅涉及簡單的物理化學知識，計算過程簡單且直接。然而在實際的考試以及科研應用中，往往會由于基礎物理化學概念不清導致出現與此題類似的錯誤。物理化學的學習不應僅滿足于會列方程解方程，還要學會列什么方程以及為什么列這個方程，前者只要有足夠的做題量積累很容易達到，但一旦涉及實際應用便容易手忙腳亂；后者需要的則是深入的思考與探究，對于各種理論，不僅知其然，更知其所以然，才能真正窺探物理化學的美感與其背后深刻的化學思維。