基于正則化最小二乘法的接地網腐蝕狀態評估方法

詹花茂 ,郭明鑫 ,劉春江 ,王 偉

(1.華北電力大學新能源電力系統國家重點實驗室,北京 102206;2.國網冀北電力有限公司唐山供電公司,唐山 063000)

變電站接地網常年埋設在地下,運行條件較復雜,一旦發生故障,就會威脅人員安全并造成嚴重的經濟損失。由于故障點隱蔽性強,無法通過測量接地電阻準確判斷故障位置和評估腐蝕程度。因此,需要研究一種可靠、簡便的腐蝕評估方法,能夠在不停電和不大面積開挖的情況下,對接地網的腐蝕和斷點情況進行檢測。

國外對接地網的研究主要集中在對接地電阻、跨步電壓和接觸電勢等參數的測量[1],采用接地分析軟件CDEGS和TRAGSYS,開展了接地性能相關的分析和計算,制定了接地網安全設計標準。國內主要依據DL/T 621-1997《交流電氣裝置的接地》和DL/T 475-1992《接地裝置工頻特性的測量導則》,通過接地電阻、接觸電壓、跨步電壓和最高電位梯度等參數,判斷接地網的運行情況和接地性能[2]。劉洋等[3]基于電磁場理論,對接地網導體的腐蝕情況進行了研究,通過向接地網接地引下線注入一定頻率的正弦電流,然后測量地表磁感應強度的分布情況,來診斷接地網導體的腐蝕情況。

劉渝根等[4]基于特勒根定理與電網絡理論,張曉玲等[5]基于電網絡原理和矩陣理論,建立故障方程組,借助優化方法計算各支路電阻的變化值,判斷接地網導體的腐蝕程度。隨著診斷模型不斷被改進和完善,除了采用BP人工神經網絡、變尺度法和擬牛頓法求解接地網的腐蝕診斷方程外[6-8],現代智能優化算法也被應用于接地網腐蝕的診斷中[9-12]。在現場測量試驗方面,劉健等[13]采用在可及節點中輪換電流源激勵位置的方法,對接地網故障進行診斷。劉渝根等[14]針對中、大型接地網的腐蝕診斷提出了分步分塊和逐步測量的診斷方法。

本工作基于電網絡理論,構建了關于接地網端口電阻與導體支路電阻的腐蝕評估方程,采用正則化的最小二乘法,解決了腐蝕評估方程組欠定和不適定的問題。采用Matlab軟件編程計算腐蝕后接地網的支路電阻,采用Multisim 軟件對接地網腐蝕進行模擬仿真,提出了腐蝕程度評估標準,結合仿真計算和模擬腐蝕試驗,驗證了測量節點選取原則的可行性。

1 腐蝕評估模型及算法

1.1 腐蝕評估模型

接地網等效模型如圖1所示,通過接地下引線連接接地網與電氣設備。

圖1 接地網等效模型Fig.1 Grounding grid equivalent model

接地網導體構成的電阻網絡按支路和節點順序編號,設接地網有b條支路,n個節點,接地下引線可及節點數量為k,針對圖2接地網中任意可及節點施加直流電流源激勵,新增加的支路編號為b+1。

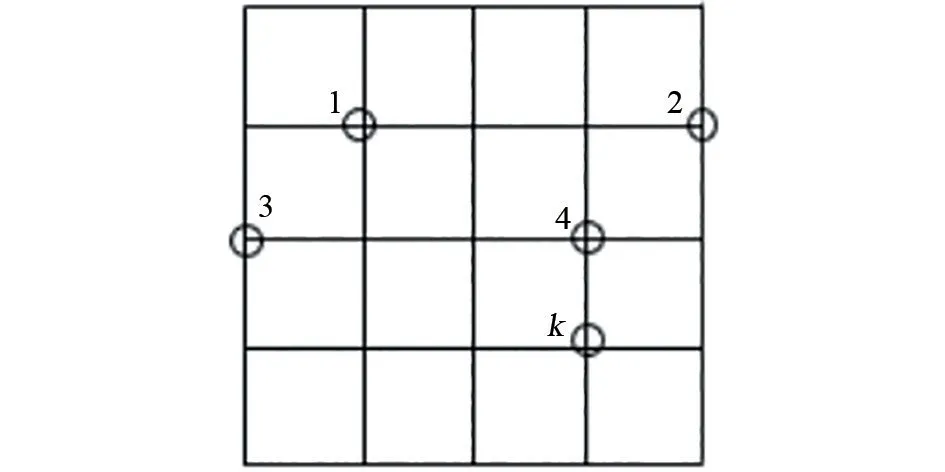
圖2 接地網中k 個可及節點示意Fig.2 Schematic diagram of k accessible nodes of grounding grid

定義該網絡的關聯矩陣為A,節點導納矩陣為Yn,支路導納矩陣為Yb,支路阻抗矩陣為R,節點電壓矩陣為Un,支路電壓矩陣為Ub,支路電流矩陣為Ib,節點注入電流列向量為In。根據電網絡理論可得關系式(1)。

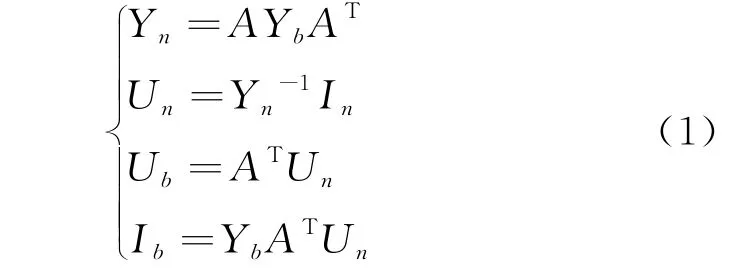
從而得出可及節點端口i和j之間的電阻Rij,見式(2)。

式中:Ub+1,Ib+1分別為第b+1條支路的電壓和電流;R1,R2,…,Rb分別對應各支路電阻。

根據特勒根定理可知,任意時刻所有支路的功率或擬功率的代數和為零,如式(3)～(4)所示[15]。

式中:Uk,Ik分別為網絡N 中第k條支路的電壓和電流;U'k,I'k分別為網絡N'中第k條支路的電壓和電流。

對于腐蝕前后兩個拓撲結構相同的網絡,在i,j端口的第b+1條支路的電流均為I0,見式(5)。

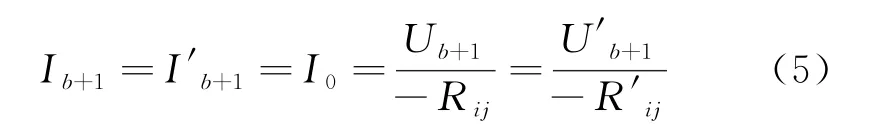
式中:I'b+1,U'b+1分別為網絡N'中第b+1條支路的電流和電壓;R'ij為網絡N'中端口i和j之間的電阻。

將式(5)代入式(3)～(4),可得式(6)～(7)。

將式(7)與式(6)相減可得腐蝕后導體支路電阻變化量ΔRk與可及節點間端口電阻變化量ΔRij的關系,見式(8)。

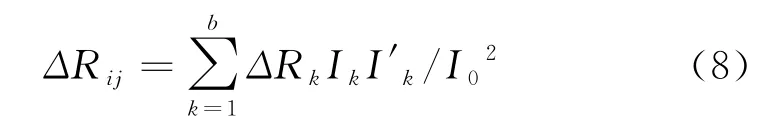
測量接地網m個端口電阻,可得m維的腐蝕評估方程組,見式(9)。

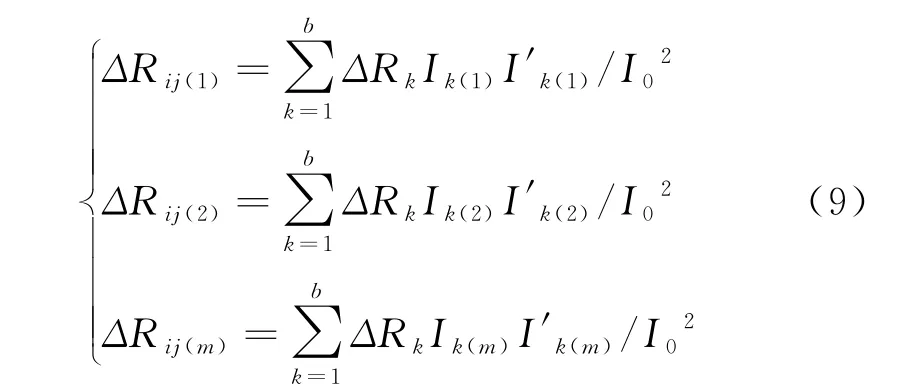
在滿足式(10)約束條件下,定義關于能量P的目標函數,見式(11)。

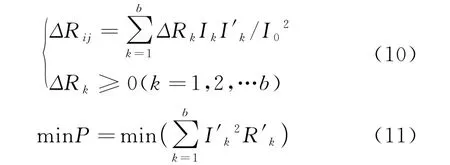
式中:R'k為腐蝕后第k條支路的電阻。

對于第2個約束條件,腐蝕后導體的有效橫截面積減小,即腐蝕后導體的支路電阻增大。對于目標函數,當電流經接地網流入大地時,整個接地網的主要能量損耗全部來源于導體電阻的消耗,故接地網各支路電阻產生的能量損耗滿足能量損耗的最低原理[8]。

1.2 Tikhonov正則化算法

采用腐蝕評估方程求解時,測量等誤差導致方程組存在擾動,測量端口數量受可及節點限制,故不能涵蓋所有可及節點的信息。本工作采用基于正則化的最小二乘法來評估方程求解欠定和不適定的問題。正則化方法是通過對目標函數添加罰項,使得求解新目標函數的極小元問題為適定問題。

應用于腐蝕評估方程時,式(9)的方程組變為求解極小化的Tikhonov正則化泛函數minJλ(x)[16],見式(12)。

式中:λ為正則化參數,為了控制數據的擬合程度和平衡關于解x的大小,λ的取值需要保持泛函數的平衡;L為正則化矩陣,用于控制解的光滑度。

當L為單位矩陣時,得到的解是最小能量或長度上的近似解[17],故設L為單位矩陣,則式(9)滿足關系式(13)。

式中:I為單位矩陣。

因為ATA是半正定的,當λ＞0 時,則可得式(14)。

本工作采用L-曲線法確定λ,由式(12)可知,‖Ax-y‖和‖x‖均是λ的函數,選取不同的λ值,以lg‖Ax-y‖為橫坐標,lg‖x‖為縱坐標,利用對數的形式推導λ,令ρ=lg‖Ax-y‖,θ=lg‖x‖,則最大曲率作為λ的函數定義為式(15)。

式中:ρ',ρ″,θ',θ″分別為ρ和θ的一階和二階導數。

對式(15)求最大值cmax(λ),即曲率最大時對應的λ值才能保證部分‖x‖和數據擬合部分‖Axy‖的平衡[18]。

1.3 腐蝕評估方程的求解

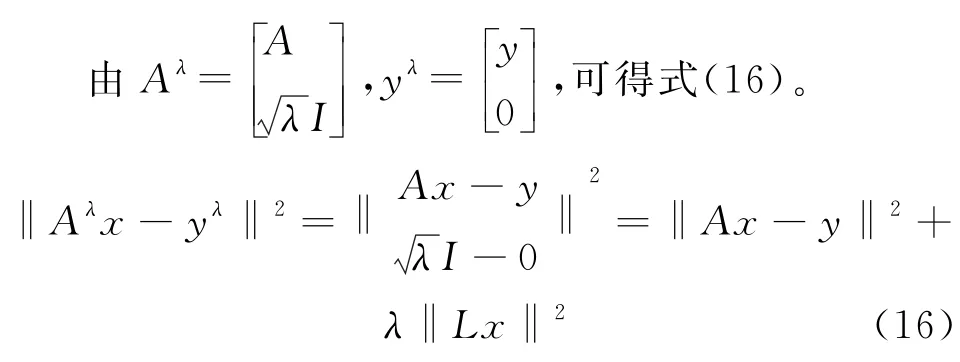
式(12)可轉換成如式(17)所示的最小二乘問題。

利用最小二乘法可得該問題的正則化最小二乘解,通過Matlab編寫程序進行診斷計算,診斷流程如圖3所示。

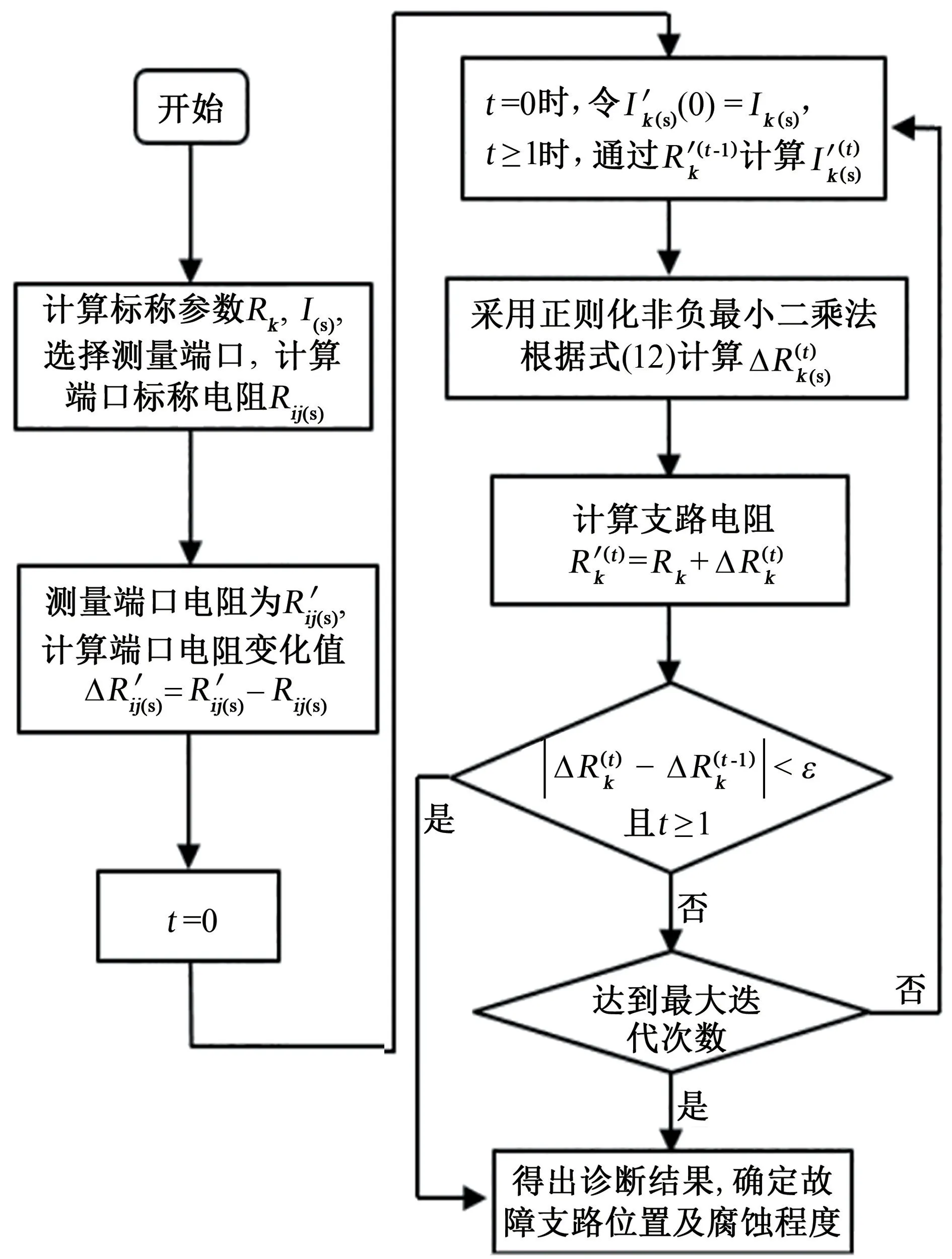
圖3 診斷流程Fig.3 Diagnostic process

采用正則化最小二乘法,求解腐蝕后接地網支路電阻的變化量,解決了腐蝕評估方程組欠定和不適定的問題,通過測量部分可及節點端口電阻,計算接地網導體的支路電阻,以實現對接地網腐蝕狀態的評估。

2 腐蝕評估方法

2.1 腐蝕評估程度劃分

如圖4所示,通過小型網絡進行仿真計算,該接地網共有16個節點和24條支路,圓圈中的數字為節點編號,其余為支路編號。設置正常支路電阻為0.05 Ω,采用Multism 軟件對接地網部分可及節點的端口電阻進行仿真計算,如圖5所示。腐蝕后接地網支路電阻隨著腐蝕程度的加劇而增大一定的倍數,接地網腐蝕越嚴重,支路電阻增大倍數越大。

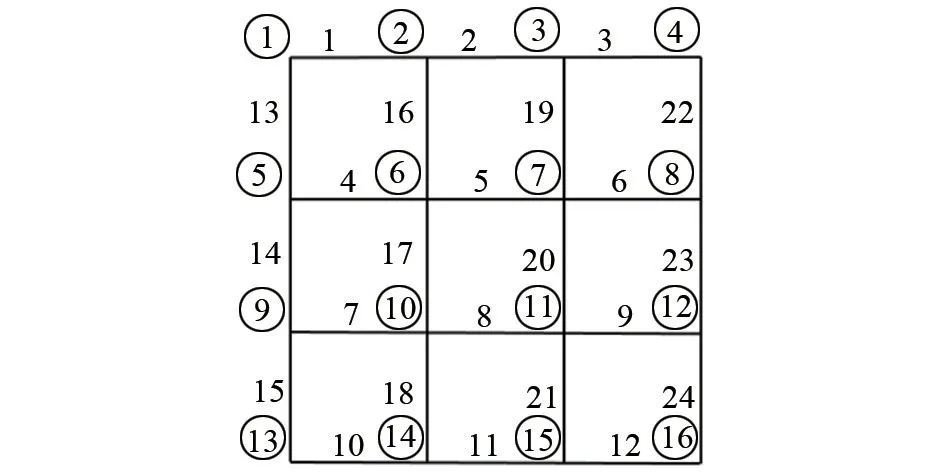
圖4 小型網絡拓撲結構示意Fig.4 Schematic diagram of small network topology

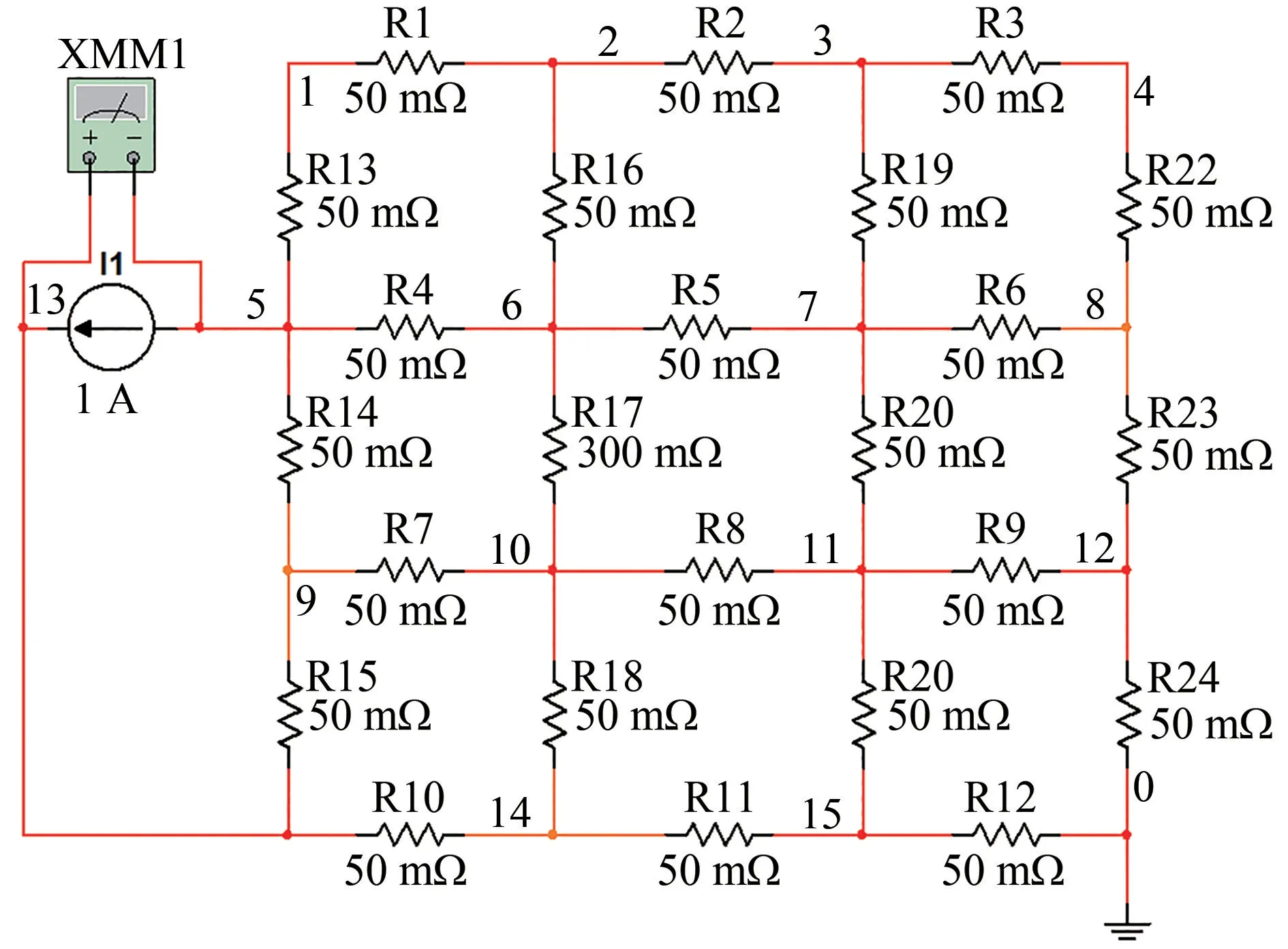
圖5 小型網絡支路電阻仿真計算結果示意Fig.5 Schematic diagram of simulation calculation results of branch resistance of a small network

設置腐蝕故障支路為支路17,對腐蝕后可及節點2,5,7,10,12,13的端口電阻進行測量,按照腐蝕評估診斷程序進行計算,分析支路電阻的設定值和計算值之間的關系。考慮腐蝕程度與支路電阻之間的關系,使支路電阻分別擴大為原來的2,3,4,5,6,7,15,24倍,按照腐蝕評估程序進行計算。由圖6可知,當支路17發生腐蝕故障時,腐蝕后導體面積縮小比例為50%,支路電阻為正常設定值的2倍,支路17的電阻增大倍數為1.68,可判斷支路17發生腐蝕故障。

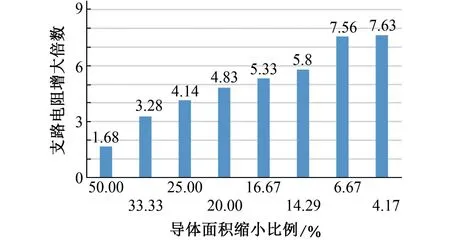
圖6 腐蝕后導體面積縮小比例和支路電阻增大倍數之間的關系Fig.6 Relationship between reduction ratio of conductor area and increase multiple of branch resistance after corrosion

分析圖6中的計算結果,考慮支路電阻增大倍數的計算值與接地網導體面積縮小比例的關系,可對接地網導體的腐蝕程度進行劃分。以腐蝕后導體面積與原導體面積的比值(s)作為衡量接地網腐蝕程度的標準,劃分為輕微腐蝕、中度腐蝕和嚴重腐蝕。令α=R'/R(α為腐蝕后支路電阻R'與正常情況下支路電阻R的比值),如表1所示。

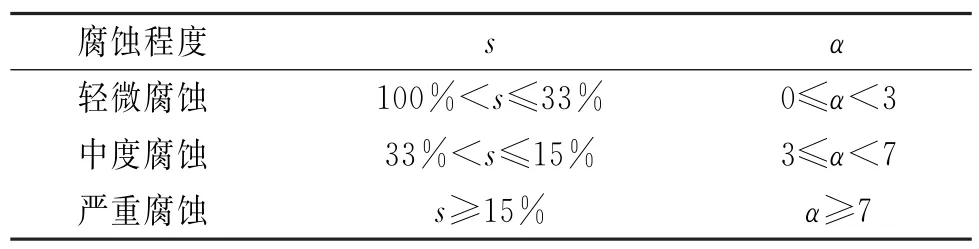
表1 接地網導體腐蝕程度劃分Tab.1 Classification of corrosion degree of grounding grid conductor

通過測量可及節點端口電阻,對接地網各支路電阻進行計算,再通過腐蝕程度劃分標準對導體腐蝕程度進行評估,得到接地網當前的腐蝕狀態,實現了對接地網腐蝕狀態的評估。

2.2 測量節點選取原則

變電站中接地網下引線數量較少,測量所有可及節點端口電阻的難度較大,腐蝕評估過程中,端口電阻數量較少引起的評估方程欠定對評估結果的精度影響較大,故需確定測量節點選取原則,以準確評估接地網的腐蝕狀態。

針對不同節點類型(跨距較小端口、跨度較大端口、接地網邊緣端口、接地網中心端口、接地網對稱交叉線上的端口、端口是否涵蓋故障支路節點和端口分布集中度)條件下,測量可及節點端口電阻。在此基礎上分別測量6,5,4,3個可及節點的端口電阻,分析測量節點數量對腐蝕狀態評估結果的影響及不同節點類型條件下腐蝕狀態評估的準確度,從而選取適用于該方法的最少可及節點數量。設置支路17發生腐蝕故障,正常支路電阻為0.5 Ω,腐蝕程度為嚴重腐蝕。

基于以上思路,針對不同節點類型條件下選取6個可及節點開展試驗。由表2可見:在16個節點中選擇6 個節點作為可及節點,占節點總數的37%;第1,3,4組選取的節點分布都較為均勻,故可以準確判斷故障位置,對于支路腐蝕程度的評估也符合設定;對于第2組選取的節點,由于節點1,16的位置均在網絡端部的頂點處,跨度較大,節點分布不均勻,會造成誤診,故不能準確反映故障支路位置及腐蝕狀態。該組診斷結果表明,測量節點不宜橫跨對角線,所有測量節點端口不能過于集中。

表2 選取6個可及節點條件下接地網腐蝕腐蝕狀態的診斷結果Tab.2 Diagnosis results of corrosion state of grounding grid under the condition of selecting 6 accessible nodes

針對不同節點類型條件下選取5個可及節點開展試驗。由表3可見:在16個節點中選擇5個節點作為可及節點,占節點總數的31%;對于第2組選擇的可及節點,由于節點間跨度大,橫跨整個接地網絡,節點端口位置集中在接地網邊緣,沒有對中部節點進行測量,故不能準確判斷故障支路位置及腐蝕程度。該組診斷結果表明,選取的測量節點應包含網絡中部與邊部節點,且測量節點應平均分布整個網絡。

表3 選取5個可及節點條件下接地網腐蝕腐蝕狀態的診斷結果Tab.3 Diagnosis results of corrosion state of grounding grid under the condition of selecting 5 accessible nodes

針對不同節點類型條件下選取4個可及節點開展試驗。由表4可見:在16個節點中選擇4個節點作為可及節點,占節點總數的25%;選取(2,3,4,8)節點測量端口電阻,由于節點分布在接地網邊緣,且端口過于集中,對于支路的腐蝕狀態存在誤判情況,故不能準確判斷故障支路位置及腐蝕情況。將能夠準確診斷與不能診斷故障支路位置和腐蝕程度的節點類型進行對比,測量節點選取應遵循接地網邊部節點與中部節點相結合、可及節點平均分布和節點間跨距不宜過大的原則。

表4 選取4個可及節點條件下接地網腐蝕腐蝕狀態的診斷結果Tab.4 Diagnosis results of corrosion state of grounding grid under the condition of selecting 4 accessible nodes

針對不同節點類型條件下選取3個可及節點開展試驗。由表5可見:在16個節點中選擇3個節點作為可及節點,占節點總數的18%;第5組選取的節點均為全部故障支路相關節點,屬于特殊情況,故在節點的選擇過程中,可事先預判最可能出現腐蝕故障的支路位置,重點對這些支路節點進行測量,實現對可及節點的充分利用及腐蝕狀態的最優化評估。一般情況下,測量節點選取應遵循接地網邊緣節點與中部節點相結合和可及節點平均分布的原則。

表5 選取3個可及節點條件下接地網腐蝕腐蝕狀態的診斷結果Tab.5 Diagnosis results of corrosion state of grounding grid under the condition of selecting 3 accessible nodes

結合以上分析,總結出以下幾條接地網測量節點選取原則(以85條支路和50個節點的中型接地網為例)。

(1) 重點原則,盡可能選擇靠近易發生故障支路的節點。在接地網腐蝕狀態的診斷過程中,為減少選擇的盲目性,要重點檢測容易出現泄漏電流和故障電流的區域和設備。

(2) 測量節點數量占節點總數的比例大于20%,選擇的測量節點端口跨距不超過4個節點長度。在變電站接地網腐蝕狀態的初步診斷過程中,減小測量時所用的導線長度,使測量工作量大大減少。

(3) 部分原則,按接地網實際規模將其劃分為4個區域,每個區域網絡中的端口數量均勻分布,進行分區測量,具有導線移動距離短、導線長度短和移動靈活、方便等優點。

如圖7所示,將85條支路和50個節點的接地網劃分為4個區域,按照縮短跨距的原則選取節點5,9,12,20,24,27,31,40,43,48共10個節點,占節點總數的20%,設置腐蝕故障支路為支路17。

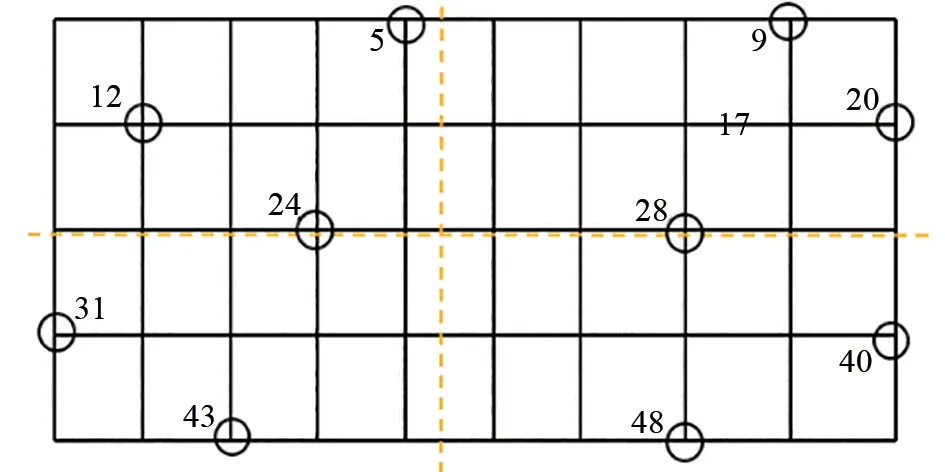
圖7 85條支路和50個節點接地網可及節點選擇示意Fig.7 Schematic diagram of selection of accessible nodes in grounding grid with 85 branches and 50 nodes

3 接地網腐蝕評估仿真計算應用

3.1 單支路腐蝕評估仿真計算

采用Multisim 軟件對圖7中的網絡進行腐蝕評估仿真計算,仿真計算結果見圖8。接地網共85條支路,50個節點,設置仿真故障參數包括支路電阻5 mΩ,腐蝕支路電阻為27 mΩ,腐蝕故障支路為支路17,腐蝕程度為中度腐蝕。

圖8 85條支路和50個節點接地網腐蝕后的支路電阻仿真計算結果示意Fig.8 Simulation diagram of simulation calculation results of branch circuit resistance after corrosion in a grounding grid with 85 branches and 50 nodes

采用正則化最小二乘法,并結合目標函數與端口電阻仿真計算結果,可求出λ為0.000 057,再按照2.3節中的診斷流程計算各支路電阻的增大倍數。由圖9可見,腐蝕支路17的電阻為24.91 mΩ,增大倍數為3.98,根據腐蝕程度評估標準,評估支路17發生中度腐蝕,這與仿真故障設置參數一致。

圖9 85條支路和50個節點接地網單條支路腐蝕后的支路電阻增大倍數Fig.9 The multiple of branch resistance increase of single branch after corrosion in a grounding grid with 85 branches and 50 nodes

3.2 多支路腐蝕評估仿真計算

考慮接地網有2條支路均發生腐蝕,支路電阻為5 mΩ,設置支路17和59發生腐蝕故障,故障支路電阻為100 mΩ,其增大倍數為19,腐蝕程度為嚴重腐蝕。由圖10可見,該接地網支路17,59均發生腐蝕。對于兩條支路同時發生嚴重腐蝕的情況,通過上述腐蝕評估方法能準確診斷出腐蝕支路位置及腐蝕程度。

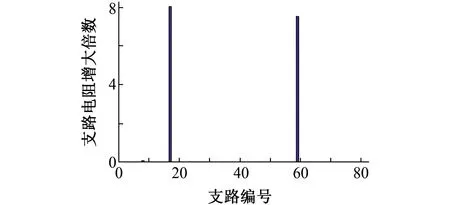
圖10 85條支路和50個節點接地網多條支路腐蝕后的支路電阻增大倍數Fig.10 The multiple of branch resistance increase of multiple branches after corrosion in 85 branches and 50 nodes grounding grid

20 ℃時,鋼材的電阻率(ρ)取0.1×10-6Ω·m,根據電阻計算公式(18),可得其電阻為5 mΩ。

式中:l為電阻長度,m;s為電阻的橫截面積,m2。

用鐵絲網模擬接地網支路腐蝕,鐵絲網材料的電阻率與變電站接地網鍍鋅鋼的相似,經測量,鐵絲網每條支路電阻為6～7 mΩ。對圖7中的網絡進行腐蝕評估試驗,將鐵絲網中的支路17剪斷,測量端口電阻,將測量值代入2.3節中的診斷流程,計算各支路電阻的增大倍數。由圖11可見,支路17的電阻是原支路電阻的7.45倍,腐蝕程度為嚴重腐蝕,這與實際情況相吻合,表明用鐵絲網模擬接地網支路腐蝕能夠準確診斷其腐蝕支路位置和腐蝕程度。

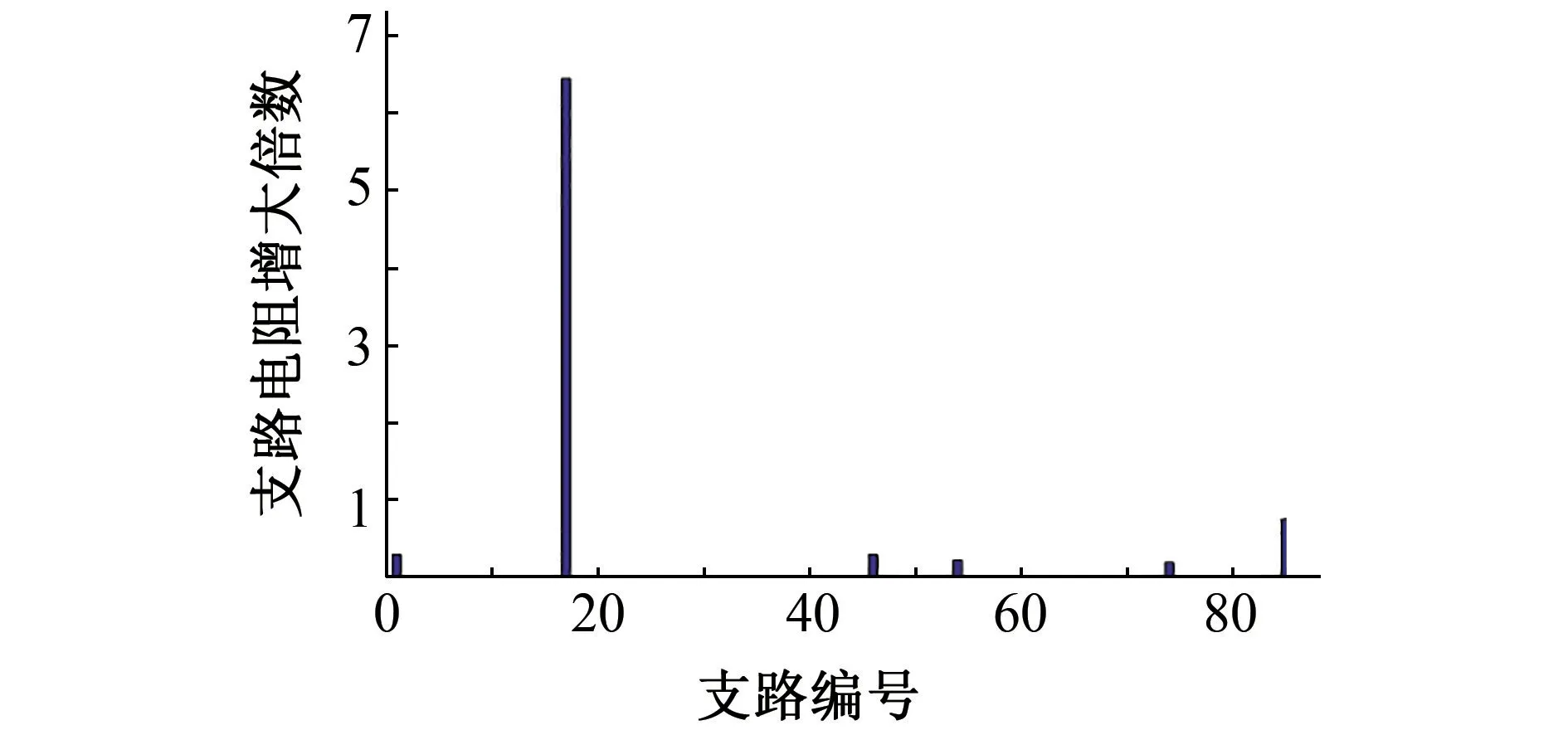
圖11 鐵絲網模擬接地網支路腐蝕的支路電阻增大倍數Fig.11 The multiple of branch resistance increase of wire mesh simulation grounding network branch corrosion

4 結論

(1) 基于電網絡理論,構建關于接地網端口電阻與導體支路電阻的腐蝕評估方程,采用正則化最小二乘法,解決了評估方程欠定和不適定的問題,當腐蝕后導體面積僅縮小比例為50%時,支路17電阻的增大倍數為1.68,可判斷支路17 發生腐蝕故障。

(2) 以腐蝕后支路導體面積與原導體面積的比值作為衡量接地網腐蝕程度的標準,接地網導體腐蝕程度可劃分為輕微腐蝕、中度腐蝕和嚴重腐蝕。

(3) 針對85 條支路和50 個節點的中型接地網,提出了接地網測量節點選取原則,選取測量節點數量大于總數的20%。

(4) 在單支路腐蝕和多支路腐蝕條件下,依據測量節點選取原則,均可準確診斷出85 條支路和50個節點接地網腐蝕支路位置及腐蝕程度。