基于改進引力模型的城市規劃用地布局環境適宜性評價研究

葉楚維

廣州市城市規劃勘測設計研究院 廣東 廣州 510000

當前，城市化進程仍處在發展時期，在可持續發展的理念下，對于城市用地布局的規劃也越來越注重環境影響[1]。依據國家頒布的《城市用地分類與規劃建設用地標準》，城市規劃的過程中，除了基本的居住用地和工業用地外，還需要充分考慮地質環境因素的影響[2]。基于此，對于城市規劃用地布局的環境適宜性進行評價，能夠更加科學合理地安排城市建設方向與空間資源的利用[3]。對于城市用地評價的系統化研究也越來越受到各界關注，成為當前學界的研究熱點之一[4]。傳統的城市規劃用地布局評價中的引力模型城市間引力不對稱的存在局限性[5]，在對其布局的環境適宜性評價的過程中，評價結果存在極大偏差[6]，為此本文提出基于改進引力模型的城市規劃用地布局環境適宜性評價研究。

本文設計相對引力常量優化的城市布局環境適宜性評價模型，依據城市質量指標公式，建立以城市競爭力為基礎的引力模型，基于此，本文采用相對引力常量，解決傳統模型中城市之間引力不對稱的問題，實現對引力模型的改進。

1 相對引力常量優化的城市布局環境適宜性評價模型設計

1.1 建立以城市競爭力為基礎的引力模型

為建立城市競爭力為基礎的引力模型，本文依據城市質量指標公式，表示出各種影響因素之間的關系，其具體計算公式表示如下：

公式中，i表示的是影響因素的數量參數；j表示的是其中的某一因素；Qi表示的是因素的權重參數；Wj表示的是因素j的標準化參數。基于上述計算公式，需要考慮城市間實際的路程與時間概念，那么城市距離B的計算公式可以表示為：

其中，q表示的是一定輻射范圍內的城市數量參數；r表示的是其中的某一城市；ard表示的是城市d與r之間的公路長度參數；brd表示的是d與r之間進行交通的平均時間參數；crd表示的是d與r之間進行交通的經濟成本參數。

基于上述兩關系量，并針對城市間的競爭力衡量城市的引力，本文建立的引力模型如下：

式中，Aq、Aw表示的分別是城市q、w的質量；Bqw表示的是q、w的距離，兩參數可以根據上述公式（1）和公式（2）計算得出；v表示的是引力常數。基于上述計算公式，我們建立了以競爭力為基礎的城市引力模型。

1.2 采用相對引力常量優化城市間引力不對稱

城市與城市間的引力關系中，引力大的城市競爭力也相對較高，我們假設引力大的城市C與相對較小的城市D之間引力指向方向為標準，以相對引力常量P代替傳統的引力參數，P的公式表示為：

公式中，G表示的是轉換系數的參數值；表示的是單位的引力矢量參數；S表示的是調節系數的參數值。

模型中原有的引力常數表示的是多種因素對城市的吸引力影響，基于上述引力常量，不同城市間的吸引力的方向是不同的，也就是說，P值隨著計算的城市的不同而變化的。我們假設城市C與城市D之間的引力相同，那么在此時，二者間的引力是對稱的，此時的引力關系公式可以表示為：

公式中，q表示的是一定輻射范圍內的城市引力影響因素的數量參數，p表示的是q中的某一因素，Ep表示的是該因素對引力常數的影響權重參數；Rp表示的是p的城市引力影響因素參數。

基于上述公式，改進后的引力模型的公式表示如下：

1.3 構建用地布局適宜性評價的數學模型

在改進后的引力模型的基礎上，本文構建了對于城市規劃用地布局的環境適宜性評價的數學模型。首先,根據國家規定的城市規劃用地的相關標準對實際的城市環境進行分析，確定影響城市環境適宜性的相關因素，基于此，本文建立了相應的評價指標體系，具體情況如表1所示。

表1 環境適宜性評價指標體系

在確定好環境適宜性的影響因素后，為實現對城市用地布局規劃的評價，需要確定各個因素的權重指標。本文采用層次分析法，對上述各個因素進行專家打分，本文對各個適宜性因素進行分級，共分為5個等級，并進行相應的量化分值賦值，重要程度越高，分值也就越高，反之越低。依據上述權重對城市規劃用地布局的環境適宜性進行評價。

1.4 模糊綜合評價法實現環境適宜性評價

在建立好評價模型，確定評價指標權重之后，就可以進行對于環境適宜性評價。由于對于城市環境適宜性的影響因素眾多，且各個因素間相互疊加，使得其內部的界限是不清晰的，因此，本文基于模糊數學理論，使用相應的綜合評價法進行評判。該評價方法流程如圖1所示。本文需要建立相應的評價模型，具體方法如下：

圖1 環境適宜性評價流程圖

首先，依據前文的評價指標體系，建立評價對象的因素集，設指標層內的各個評價因素為w，那么其組成的因素集可以表示為W=(w1 ,w2 ,… ,wn)。

其次，本文依據專家評價標準，將城市規劃用地布局的環境適宜性進行等級劃分，假設環境適宜度的評價等級為e，那么其組成的評判集可以表示為E=(e1 ,e2 ,… ,en)。

之后，本文根據相關的隸屬度，建立了W與E之間的模糊映射，構造隸屬關系的模糊矩陣U，其公式表示如下：

結合上述關系矩陣，確定各個評價等級的權重k，其集合可以表示為K=(k1 ,k2 ,… ,kn)。

然后，依據改進的引力模型對城市的經濟環境、建設環境、交通環境以及自然環境等不同條件的適宜性進行評價，假設適宜度為u，相應的計算公式表示為：

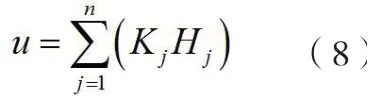
式中，n表示的是適宜性的評價因子的數量參數；Kj、Hj分別表示的是其中某一因子j的指標參數值和權重參數。

依據上述方法，能夠建立評價模型，實現對于環境適宜度的綜合評價，輸出最終的評判結果。

2 實驗

2.1 實驗準備

為了進行環境適應性評價，本文依據上述方法，以某城市G的城市規劃方案為實驗對象，對其進行評價。

首先，收集一定區域內城市的數據，并根據當地區域的實際城建情況，在分析該城市與相鄰城市的經濟發展情況的基礎上，選取能夠進行評價的數據作為評價的指標層。在選取的數據集范圍內對數據進行處理，依據本文分析方法，確定環境適宜性的評價指標，具體情況如表2所示。

表2 評價指標參數表

在確定好評價指標后，本文參考原有的環境適宜性評價等級，將適宜性進行分級，分別為Ⅰ級、Ⅱ級、Ⅲ級、Ⅳ級以及Ⅴ級。依據上述評價指標體系，對G市的城市規劃用地布局環境適宜性進行評價，G市的城市規劃用地布局面積為2967km2，依據上述評價原則與評價指標，分別使用傳統的引力模型評價方法，與本文設計的評價方法，對G市的城市規劃用地布局環境適宜性進行評價，記錄相應的評價結果。

2.2 實驗結果分析

根據上述實驗，本文記錄了兩種方法下，對G市城市規劃用地布局環境適宜性的評價結果，具體實驗結果數據如表3所示。

表3 不同方法的規劃用地布局環境適宜性評價結果

上表中的評價等級的劃分，是依據實驗準備階段中劃分的評價等級建立，具體情況見表5。由上述實驗結果表可以看出，RSEI-熵權法與本文設計方法所輸出的評價結果差別較大。本文設計的方法在進行評價時準確性明顯高于傳統方法。分析RSEI-熵權法評價結果，可以看出，其在適宜性等級規模的劃分方面，輸出結果較為籠統，尤其是在對于Ⅱ級較適宜區域與Ⅴ級不適宜區域這兩種等級進行劃分的時候，結果準確性受限，實際輸出的評價結果在規模方面誤差較大。而相比較于RSEI-熵權法，本文設計的評價方法在進行適宜性評價的過程中，其等級劃分較為精準，并且，本文設計方法能夠針對較不適宜區的布局，評價出較準確的規模范圍，也能夠具體識別出不適宜的規劃布局的規模范圍，評價的結果輸出方面，明顯更具優勢。

3 結束語

為提高城市規劃用地布局環境適宜性評價的準確性，本文在改進引力模型的基礎上，設計了新的評價方法，建立了相對引力常量優化的城市布局環境適宜性評價模型，實現了本文設計。并通過對比傳統評價方法，驗證了本文設計的評價方法在對城市規劃用地布局環境適宜性評價方面的應用價值。證明了本文設計方法評價等級劃分更為精準、評價結果更為準確客觀。