選擇路徑組合方法 提高數學運算素養

瞿 晶

(南京市第二十九中學)

《普通高中數學課程標準(2017 年版2020 年修訂)》指出:數學運算是指在明晰運算對象的基礎上,依據運算法則解決數學問題的素養,主要包括理解運算對象、掌握運算法則、探究運算思路、選擇運算方法、設計運算程序、求得運算結果.

在解析幾何的解題過程中,以形助數或以數思形,通過數形結合的思想方法,建立數與形之間的聯系,是學生需要培養的運算素養.圖形分析與研究能力是探索問題、解決問題的思路源泉,圖形研究的能力培養主要有兩方面:一是能從不同的角度描述圖形的特征;二是研究圖形與圖形之間的關系,其中最主要的關系就是圖形之間的位置關系和數量關系.其中,位置關系有直線與直線相交、平行等;數量關系有線段的長度、角的大小、三角形的面積等.

解析幾何的本質就是用代數方法研究幾何問題.在解題過程中,由于幾何條件代數化可以選擇不同的代數路徑進行轉化,對一個題目中相應的幾個幾何條件轉化時,使用不同的路徑則可以組合出不同的解法,從而形成一道題目的不同解法.在此基礎上,我們選擇其中較為簡潔的轉化方式,設計簡潔的運算路徑,組合成較為快捷的運算方法.

1 問題

題目已知點A,B在橢圓＝1(a＞b＞0)上,點A在第一象限,O為坐標原點,且OA⊥AB,若△OAB為等腰三角形(點O,A,B按順時針排列),求的最大值.

解析方法1因為△OAB是等腰直角三角形(點O,A,B按順時針排列),所以設A(x1,y1),B(x2,y2)(x1＞0,y1＞0,x1＜x2).

將等腰直角△OAB的條件等價轉化成OA＝AB且OA⊥AB,其中OA＝AB可以利用兩點間距離公式進行轉化,OA⊥AB可以利用斜率之積等于－1進行轉化,由此得到點B的坐標為x2＝x1＋y1,y2＝y1－x1,轉化過程如圖1所示.

圖1

方法2將等腰直角△OAB的條件等價轉化成OA＝AB且OA⊥AB,然后利用平面幾何的相似性將方法1的步驟簡化,得到點B的坐標為x2＝x1＋y1,y2＝y1－x1,在代數運算過程中,可以通過結構的對稱性直接轉化為關于x1,y1的齊次式,再轉化為關于的一元函數求最大值的問題,轉化過程如圖2所示.

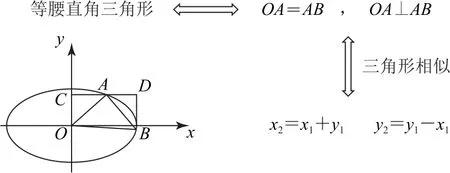
圖2

作AC⊥y軸,AD⊥BD,可得△OAC≌△ABD,所以OC＝AD,AC＝BD.

設A(x1,y1),B(x1＋y1,y1－x1),下同方法1.

方法3將等腰直角△OAB的條件等價轉化成∠AOB＝45°且OB＝,其中∠AOB＝45°運用正切的兩角和差公式進行轉化,OB＝運用兩點間距離公式進行轉化,轉化過程如圖3所示.

圖3

設直線OA的斜率為k(k＞0),傾斜角為θ(0°＜θ＜90°).因為△OAB是等腰直角三角形(點O,A,B按順時針排列),且OA⊥AB,所以直線OB的斜率為kOB＝tan(θ－45°),所以

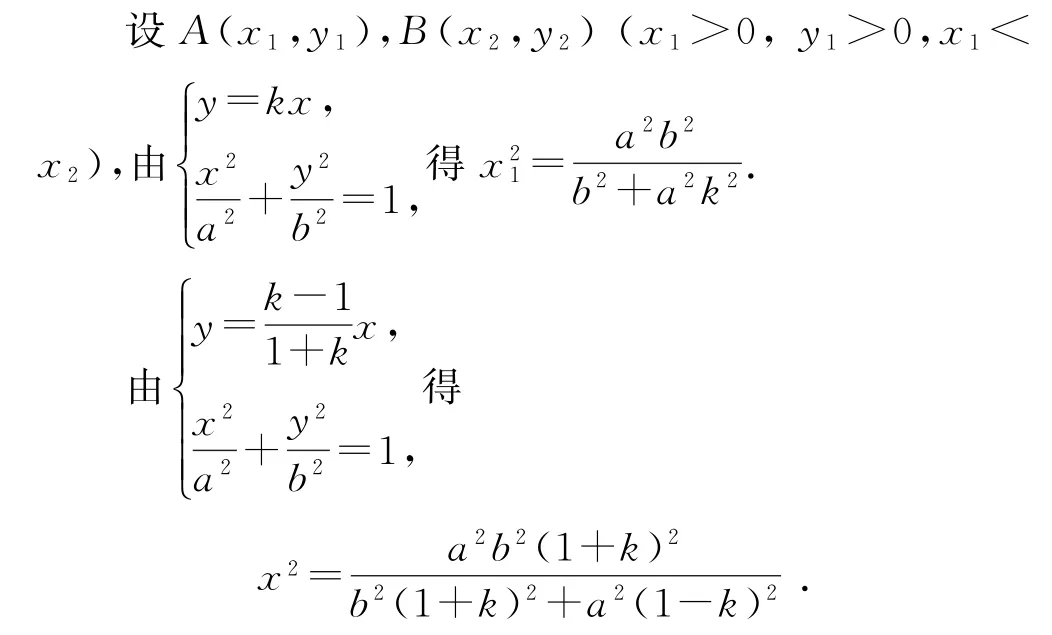
整理得b2k2＋2(b2－a2)k＋a2＝0,下同方法1.

方法4將等腰直角△OAB的條件等價轉化成M為AB中點,且tan∠AMO＝2,再通過斜率關系進行代數轉化,運算量較小,轉化過程如圖4所示.

圖4

2 反思

在實施運算分析和解決問題的過程中,要善于分析運算條件、探究運算方向、選擇運算方法、設計運算程序,使運算符合算理,且合理簡捷.換言之,運算能力不僅是一種數學操作能力,更是一種數學思維能力.

如何合理地翻譯幾何條件,通過轉化等式的多樣性,降低運算量,這是考查學生對于幾何問題的理解.調整或采用某種策略和表征的過程可以體現出學生的思維方式.因此,我們可采取一些有效的方法,幫助學生改進思維方式.

1)通過強化閱讀能力提高在關聯的情境中確定運算對象、分析問題的能力.

數學閱讀能力是正確理解運算對象的前提.蘇霍姆林斯基在《給教師的建議》一書中指出:“只有學會流利地、有理解地閱讀的人,才能順利地掌握知識.”認真審題是一種能力,是閱讀能力在態度上的細化表現.閱讀就是與文本對話,審題就是要閱讀題目的文本,要讀懂題目中的已知條件和未知信息、讀取題目中的數據、讀清題目所提的問題.讀懂文本是在大腦中重新建構文本,理解題目是否隱含了信息,具體又隱含了哪些信息? 數據之間有什么關系,符號代表什么意義? 為什么要這樣問,題目的文本想表達什么?認真讀題,弄清題意,將題目的外顯條件和內隱條件都充分挖掘出來,并在腦海中形成一個完整、清晰的結構,進行合理地問題表征,這樣才有可能開展有效的運算.

2)通過一題多解培養反思意識,教會學生針對問題合理選擇運算方法、設計運算程序.

只有在學生體會到怎樣想、為什么這樣想時,才可以讓知識在今后面臨類似問題時自動浮現,才能將所學知識應用于實際問題的解決.第一,要鼓勵學生進行創造性的猜想與嘗試.第二,要允許學生在提問時出錯、允許補充,意見不一時,允許學生保留自己的看法.這些過程中的所謂錯誤正是寶貴的教學資源和學生思維培養的真正著力點.第三,要善用評價,營造氛圍,使學生樂于提問.第四,學生提問后,要進一步幫助學生明晰問題,尋找問題的本質,使學生提高思維能力和表達能力,進而學會問問題.

3)重視基礎知識的生成、建構、延展,使學生能理解運算是一種演繹推理,在綜合運用運算方法解決問題的過程中體會程序思想的意義和作用.

數學運算的實質,就是根據運算相關的定義、公式、法則,利用已知數據及算式推導出結果.在此過程中,學生如果遺忘或混淆概念、公式、法則,則必然影響運算結果的正確性.首先,教師應該重視課堂教學中基礎概念的生成過程,在學生已有的認知基礎和生活經驗上進行教學,使其充分感知和經歷知識再創造的過程.其次,教師應該創造恰當的情境,引導學生自發地對所學知識進行歸納與梳理,并主動構建更完備的知識體系.最后,教師要根據學生的學科發展情況,對基礎知識進行適當推廣和延展,增加學生所掌握知識的延伸性,使學生能夠在計算過程中優化過程、提高運算正確率.

4)通過提升語言表達能力和書面表達能力來提高運算素養.

表達與交流能力是邏輯推理素養的重要組成部分.學生能否精準地表述問題、能否有條理地進行推理、能否正確地運用數學語言簡化表達,都會影響運算的過程.運算過程中不僅要教會學生有邏輯地思考問題,還要培養學生能厘清運算的過程、明晰運算的思路的能力,并能準確地表述和交流,從而進一步提高運算素養.

首先,要教會學生將自然語言轉化為數學語言.學生要學會從題目文本描述中提煉數學問題,抽象出解決問題所需的關鍵信息.其次,要教會學生簡化語言、清晰表達.根據費曼學習法,如果學生能夠用簡單的語言表述,讓其他學生聽明白某個問題,那么說明他真正理解了.如果他的解釋冗長而復雜,那說明他對問題的理解可能并不透徹,還需要進一步思考.教師應該給不善于表達的學生提供更多的交流機會.在師生交流或生生交流的過程中,通過反問、追問等方式幫助學生提高語言表達能力,準確理解數學問題.再次,教師在教學過程中要通過規范的課堂語言和規范的解題過程,提升學生的語言表述和書面表達能力,引導學生條理清晰地運用數學語言表達運算過程,提升數學運算素養.

3 小結

波利亞說:“教學生解題是意志的教育”,因此在運算指導方面,教師的首要職責是幫助學生克服運算的畏難情緒,一些學生在面對運算問題時,信心不充分,尤其看到看似復雜的運算問題時,想要放棄,教師要幫助學生樹立信心,給學生創造運算的成功體驗.另外,克萊因也說過,鑒賞嚴密性的能力是學生年齡的函數而不是數學成熟程度的函數.讓學生不犯低級錯誤,暢談人生理想,堅定學習奮斗目標,或許比一次又一次地機械地重復教授知識點,要更加有效.

(完)