面向爆轟沖擊的分離式流固耦合數值模擬

張 森，郭曉威，*，甘新標，龔春葉，楊文祥，李 超

(1.國防科技大學計算機學院，量子信息研究所兼高性能計算國家重點實驗室，長沙 410073；2.中國空氣動力研究與發展中心，綿陽 621000)

0 引言

爆轟波的沖擊響應通常涉及高溫高壓下的流體動力學，以及固體的變形和損傷等。這一復雜過程固有的多物理和多尺度特性導致了實驗的高成本和高難度。隨著高性能計算技術和數值模擬方法的發展，對爆轟沖擊下固體響應進行數值模擬已成為一種有效的工程研究方法[1-3]。

爆轟傳播是一個典型的兩相或多相流問題。考慮到不同域（如炸藥和空氣）之間跨界面的跳躍條件，該問題的主要數值難點是精確計算界面運動，可能的解決方法包括界面跟蹤法[4]、基于界面重構過程的VOF（volume of fluid）方法[5]、水平集（level set,LS）方法[6]、擴散界面法[7-9]等。其中擴散界面法不需要計算界面的精確位置，而需要為過渡層中的混合物引入與擴散界面相對應的混合物模型或人工狀態方程。利用這一方法，Larrouturou提出了適用于理想氣體狀態方程的γ模型和質量分數模型[7]。然而，這些模型可能導致壓力或速度在界面上的振蕩。為了解決這個問題，Abgrall和Karni將γ模型的非保守方程應用于該問題[8]。Shyue通過添加更多與狀態方程中所用參數相對應的輸運方程，將該模型擴展到其他類型的狀態方程[9]。此外，離散玻爾茲曼方法（DBM）應用在爆轟燃燒領域并取得進展[10]，張玉東等基于離散玻爾茲曼模型，模擬和研究了四種不同反應速率的爆轟現象，從水動力量、非平衡量和熵產三方面研究了四種起爆方式的差異[11]。blastFoam[12-13]是Synthetik applicated Technologies基 于 開 源 軟 件OpenFOAM開發的適用于高爆轟、爆炸安全、氣流和一般可壓縮流動的單相多相可壓縮流動庫，包括13個狀態方程，允許在極端條件下對各材料進行建模。blastFoam提供了一個比較完善的功能來模擬爆轟波的傳播過程，但是無法模擬爆轟沖擊引起的固體變形和損傷。固體的損傷變形可通過固體力學進行建模計算，采用有限元方法對數學模型進行離散。開源有限元框架deal.II[14]是一個支持創建有限元代碼的C++程序庫，該程序庫包含網格處理和細化、自由度處理、網格輸入和圖形格式的結果輸出等細節。

流固耦合（fluid structureinteraction,FSI）的主要理論模型可以從流體動力學和固體力學的建模中得到。但是，除了單一的物理模型外，還需要考慮不同物理模型之間的相互作用。流固耦合數值模擬一般采用整體式或分離式方法。整體式方法將耦合系統作為整體來推導全局方程，然后用統一的方法對其進行離散求解。該方法是魯棒且高效的，但其模塊化不足，在解決新問題時無法重用已有的代碼，需要進行重構、離散化、編碼。分離式方法固有的靈活性，可以重用現有相對成熟的單物理場求解器，快速開發代碼，并能在有限的時間內快速解決問題。

分離式方法將FSI問題分解為多個域，分別求解每個子域，并通過不同域之間的接口進行耦合。分離式FSI主要包括兩個任務，即：流體與固體方程之間的耦合格式和流體與固體在界面上的數據映射。在過去的幾十年中，擬牛頓耦合方法變得越來越重要。Michler等提出的interface-Newton-Krylov方法[15]是第一個擬牛頓耦合方法。之后，Vierendeels等在塊迭代系統的基礎上，提出了界面塊擬牛頓最小二乘（IBQN-LS）耦合方案[16]，Degroote等提出了界面擬牛頓逆最小二乘法（IQN-ILS）[17]，Bogaers等提出了多矢量擬牛頓（MVQN）格式[18]。對于數據映射方法，常用的有最近鄰法、最近投影法、徑向基函數映射法等。精確代碼交互耦合環境preCICE提供了多物理耦合所需的所有組件，包括通信方法、數據映射方法以及基于擬牛頓耦合方法的高效和健壯的耦合迭代技術[19-21]。

分離式方法具有良好的功能可擴展性和靈活性，但其收斂效率和并行可擴展性通常較差。De Nayer等采用基于CoMA的分離式方法模擬了帶有柔性分流板（PfS-1a）的圓柱繞流[22]，其效率和可擴展性受順序耦合格式和集中式工具的限制，客戶端與服務器之間的通信存在瓶頸。為解決上述問題，我們基于點對點的通信布局來傳輸耦合數據，消除瓶頸。

綜上所述，本文針對爆轟沖擊下的固體響應，基于開源軟件OpenFOAM（blastFoam[12]）、deal.Ⅱ[14]、preCICE[19]實現分離式流固耦合的求解系統，兼具靈活性和可擴展性，同時采用具體實例，即三維豎直墻體在高爆轟作用下的運動過程，進行數值模擬，并對模擬結果進行分析和討論，以驗證求解系統的正確性。

1 數值方法

分離式流固耦合數值求解部分包含三個模塊，即流體計算模塊、固體計算模塊和耦合計算信息交換模塊。各個模塊的數值方法也不盡相同。

1.1 流體計算模塊

爆轟波傳播是一種高度可壓縮的超音速流動。基于OpenFOAM軟件框架和blastFoam庫，采用有限體積法對流體模型進行離散求解。

作為流體動力學的基本控制方程，Navier-Stokes（N-S）方程主要由連續方程、動量方程和能量方程三個基本物理守恒定律組成。N-S方程可以表示為：

其中，U指由體積分數、質量、動量和能量組成的矢量，F 指相應的通量，S表示源項的向量。它們被定義為：

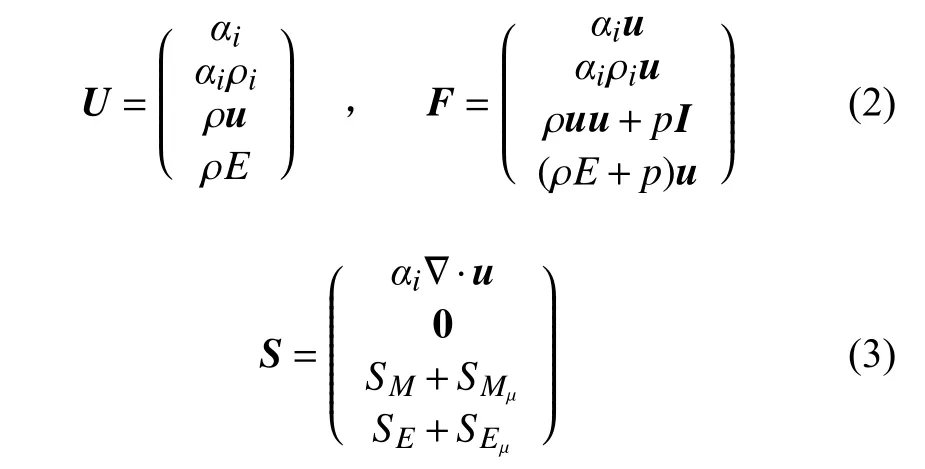
式中：u表 示混合物速度，I 表示單位矩陣，ρ指混合物密度，E 指總能量，p表示壓力，SM和SE是指動量和能量源項， SMμ和SEμ指黏性項，αi和ρi表示每相的體積分數和密度。所有體積分數之和定義為1，混合物的密度ρ由各相的體積分數和密度確定，表示為ρ=

壓力由一個特定的狀態方程來定義，在這個狀態方程中，混合物的內能、密度和體積分數被用來計算總壓力。狀態方程的Mie-Grüneisen形式使用理想氣體項和偏差項來計算壓力，即：

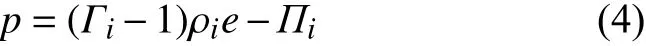
其中，Γi是Grüneisen系數，e是材料的內部能量，Πi指與理想氣體的壓力偏差。同時，聲速表示為：

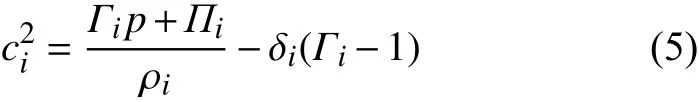
不同的材料對應不同的狀態方程。對于理想氣體，滿足Γi=γi，Πi=0；對于硬化氣體，滿足Γi=γi，Πi=γiai，其中，γi表示比熱比，ai表示參考壓力。對于高能炸藥，Jones Wilkins Lee（JWL）狀態方程是最常用的描述高能炸藥的狀態方程，系數滿足：

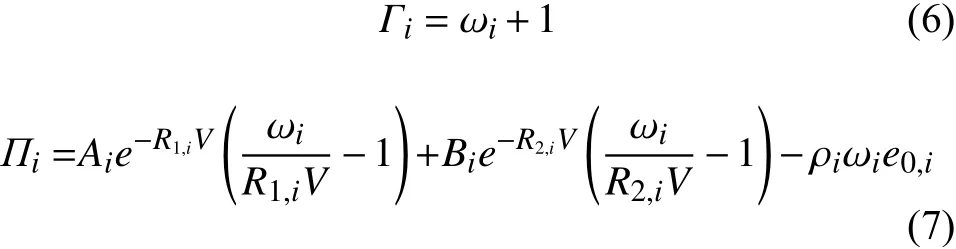
1.2 固體計算模塊

假設固體為線性彈性的，則可用彈性方程描述固體的運動。在deal.II軟件框架的基礎上，采用有限元方法對固體計算模塊進行離散求解。

控制方程主要由運動方程、本構方程和應變位移方程組成，即：

其中，σ表示Cauchy應力張量，f表示單位體積的體積力，ρ表示質量密度，d 表示位移矢量，表示d對時間的二階導數。C表示四階剛度張量，ε表示無窮小應變張量，運算符“:”表示兩個張量的內積。

在各向同性介質中，本構方程可簡化為：

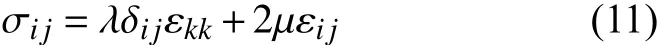
其中，λ表示Lamé第一參數，μ表示剪切模量，兩者都是Lamé參數。

在通過接口數據通信獲得應力后，可將應力代入本構方程（9）求解應變，然后代入應變位移方程（10）求解位移。最后，將經過一個時間步長后的位移通過接口數據通信發送給流體計算模塊，完成耦合交互。

1.3 耦合計算信息交換模塊

對于分離式FSI，假設兩個求解器F 以及S，分別等價于映射和S。一個求解器將耦合接口上的輸入向量映射到輸出向量，并將其發送到另一個求解器。也就是說，以固體邊界上的位移D（ 或速度V）作為流體求解器的輸入，計算作用到固體上的應力F作為輸出；固體求解器將這些應力作為輸入，并計算位移（或速度）作為輸出。數學形式表示為：

分離式流固耦合數值模擬中的時間步可以在流體或固體求解器中通過少量固定數量的時間步來完成，也可以通過迭代過程直到收斂。前者對應于顯式耦合格式，后者對應于隱式耦合格式，兩者都有串行和并行格式。

串行顯式格式首先使用舊時間步的位移值dn作為輸入來運行流體求解器，并獲得下一時間步的輸出應力值 fn+1。然后使用輸出應力值 fn+1作為輸入來運行固體求解器以獲得下一時間步的位移值dn+1，即：

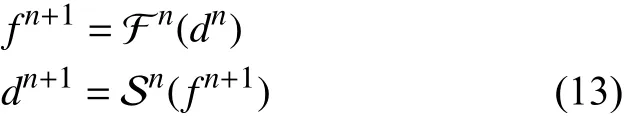
在串行顯式格式中，兩個求解器是交錯運行的，因此在負載平衡和最大化并行性方面不是最優的。并行顯式格式使用舊時間步的位移和應力值（dn,fn）作為兩個求解器的輸入，以獲得下一時間步的位移和應力值（dn+1,fn+1）：

兩個解算器之間沒有依賴關系，因此可以在同一時間步中同時執行。然而，這兩種方案都可能導致不穩定，可以使用迭代方法迭代執行兩個求解器，直到收斂。對于串行隱式格式，表達式為：

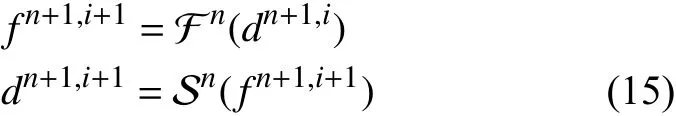
而對于并行隱式格式，表達式為：

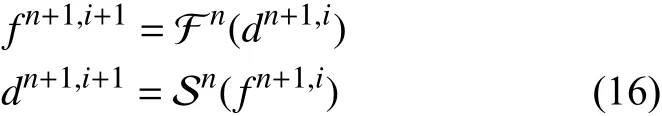
當迭代收斂時，則滿足：

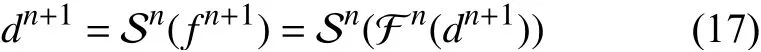
由于求解器之間相互獨立，所使用的網格在界面上可能會出現不一致的情況，因此需要在不匹配的網格之間進行數據映射。常見的數據映射方法有最近鄰映射、最近投影映射、徑向基函數（RBF）映射等。

求解器之間通信的主要任務是交換耦合數據。開源耦合庫preCICE為通信任務提供了解決方案，使用MPI或TCP/IP套接字建立通信。在耦合模擬之前，preCICE將在每個求解器進程之間建立一個通信通道，每個并行求解器將選擇一個進程作為“主進程”來控制整個數值模擬過程。在通信過程中，采用了點對點的通信方式，不使用任何中央服務器。通過先前建立的通信通道，各求解器進程之間的通信是本地和異步的[19]。

2 驗證算例的幾何構型與參數配置

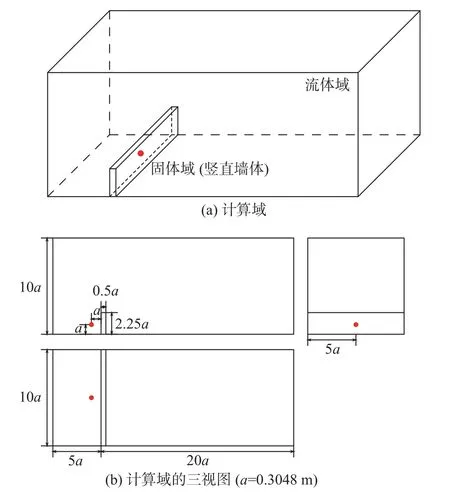
圖1 測試算例的計算域示意圖及其三視圖Fig.1 Computational domain and itsthree views

采用三維豎直墻體在高爆轟作用下的運動過程作為測試算例驗證和分析流固耦合數值模擬的求解系統。測試算例的計算域示意圖及其三視圖如圖1所示，計算域分為兩部分：流體部分和固體部分。固體部分為0.5a ×2.25a ×10a的豎直墻體，流體部分則是立方體空間內去除豎直墻體剩下的區域。紅點表示爆轟中心，距固體和下邊界的距離均為0.3048 m。在中心截面處豎直墻體周圍設置了六個采樣點，采樣點的分布情況如圖2所示，紅點表示爆轟中心，青點表示各采樣點。使用兩種不同規模的網格（分別為457.6萬和764萬個單元）進行網格無關性檢驗，結果如圖3所示。由圖中可以看出采樣點1和2處的壓力變化與網格規模無關，因此數值模擬的結果與網格規模無關。下文中除并行測試外的數值模擬結果均采用以下結構化網格，即流體網格包含466.9萬個點，1382萬個面和457.6萬個單元。爆轟中心附近和流體與固體界面處的網格較密集，遠離爆轟中心處網格較稀疏。固體網格包含64.8萬個點、59萬個面和19.2萬個單元，自由度為618723。

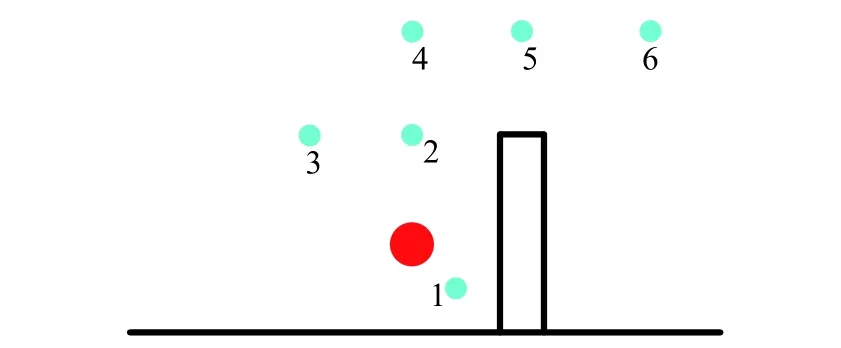
圖2 中心截面處豎直墻體周圍的采樣點分布示意圖Fig. 2 Distribution of sampling pointsaround the central section of the vertical wall

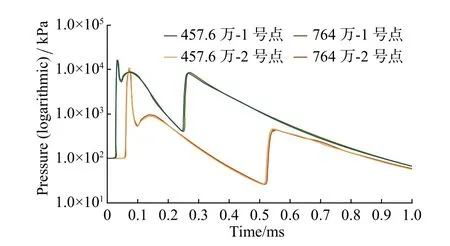
圖3 網格無關性檢驗(采樣點1和2處的壓力變化)Fig.3 Mesh independency test(pressure at sampling points1 and 2)

流體部分由兩相材料組成，即C4炸藥和空氣。各相材料的狀態方程類型及其系數值如表1所示。C4炸藥的狀態方程類型為JWL，而空氣的狀態方程類型為硬化氣體（Stiffened Gas）。對于固體部分，豎直墻體的材料由三個參數決定，即密度（ρ）和兩個Lamé參數（λ 、μ）。混凝土墻體的密度為2440 kg/m3， λ為9.03×109，μ為13.54×109；鐵板墻體密度為7000 kg/m3，λ為102.42×109，μ為80.47×109。

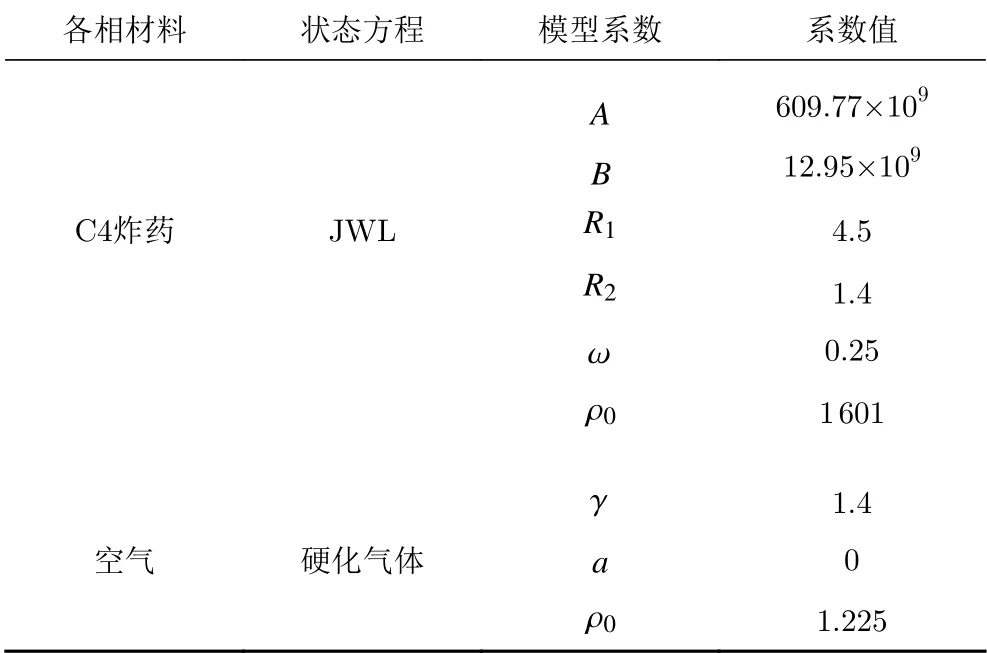
表1 流體計算模塊各相材料的狀態方程及其系數值Table1 The EOSand coefficients of each phase in the fluid module

數值格式是數值模擬的重要部分。對于流體求解器，通量格式選擇HLLC格式；一階時間導數項格式選擇二階強穩定Runge-Kutta（RK2SSP）格式；從單元中心到面中心的插值格式為cubic插值，標量的重構格式是vanAlbada，向量的重構格式是vanAlbadaV。除此之外，梯度格式為faceMDLimited leastSquares 1.0、表面法向梯度格式為corrected、拉普拉斯格式為Gauss linear corrected。對于固體求解器，選擇具有二階精度的Crank-Nicolson格式。

對于耦合計算信息交換模塊，耦合交互的數據為位移和應力，數據映射方法采用最近鄰映射。耦合格式采用串行隱式格式（方程（15）），加速格式采用IQN-ILS[17]方法。

3 結果與討論

算例是在高性能計算平臺上進行測試的，該平臺包含數百個計算節點，每個節點包含兩個Xeon E5-2620處理器（6核，2.10 GHz）。

圖4是Beyer報告中的爆轟過程定性分析圖，顯示出高能炸藥爆炸后的爆轟波傳播過程。在高爆轟作用下，豎直墻體受到較大的沖擊力，導致壁面變形。圖5是三維豎直墻體在高爆轟作用下的運動過程的整體模擬圖。該圖包括豎直墻體的位移、流場中的速度流線和密度等值線以及下邊界的速度分布。圖中豎直墻體的材質為鐵板，鐵板墻體的變形程度小于混凝土墻體。

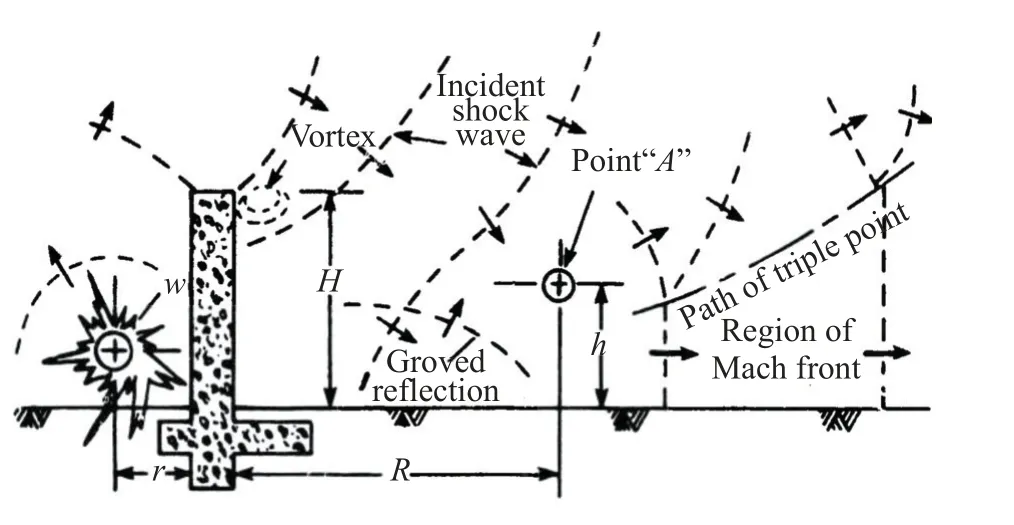
圖4 Beyer報告[23]中的爆轟過程定性分析圖Fig.4 A sketch of denotation process provided by Ref.[23]

炸藥在爆炸點起爆后很快就擴散到豎直墻體。在0.04 ms左右，爆轟波首先與豎直墻面接觸，但豎直墻面暫時沒有受到沖擊力的影響，尚未發生變形。在0.07 ms左右，豎直墻體所受到的壓力高達10.20 GPa，此時豎直墻體在爆轟接觸點處有輕微變形。從圖5可以看出，隨著時間的推移，豎直墻受到持續的應力，變形繼續從初始接觸點向外延伸。當爆轟波傳播到豎直墻體下邊界的角落處時，壓力和密度不斷積累。在0.2 ms時，墻角處的壓力為最大壓力，達到52.24 MPa，密度達到47.71 kg/m3。在0.6 ms時，豎直墻體的變形達到最大值，x方向偏移達到0.045 m。當爆轟波撞擊豎直墻體及其下邊界時，爆轟波反彈并向后傳播。爆轟波向外傳播，對豎直墻體施加力的作用，引起豎直墻體的變形。同時，由于豎直墻體的變形，爆轟波傳播的計算域發生變化，從而影響爆轟波的傳播。它們相互耦合、相互作用。爆轟波向外傳播，與豎墻相互耦合，豎直墻體右上角出現漩渦。數值模擬結果展示的爆轟過程與Beyer[23]報告的爆轟傳播過程相一致。

圖6顯示了豎直墻體在高爆轟作用下的形變過程。豎直墻體的材料為混凝土。在初始爆轟接觸點處，首先形成凹面，然后變形向外擴展。當時間為0.71 ms時，垂直墻的位移達到最大值，x方向的最大偏移達到0.157 m。隨著時間的推移，雖然墻體中間位置的x方向偏移逐漸減小，但墻體的變形范圍仍在不斷擴大。

圖7、圖8和圖9分別顯示了0.4、0.8、1.2、1.6 ms的速度流線圖、壓力等值線圖和密度等值線圖。此時，爆轟波經過下邊界和豎直墻體的反彈后繼續向外傳播。0.3 ms后，豎直墻體右上方逐漸形成渦旋，流線規則地向外輻射，壓力和密度在波面處發生躍變（包括初始波和反彈波）。當爆轟波向外傳播時，渦逐漸變大并逐步發展為梭形渦。圖7顯示了中心截面后半部分的速度流線圖，可以看出，在0.4 ms時，整個速度流線向外輻射，在豎直墻體的右上角開始出現一個小渦旋。

圖5 三維豎直鐵板墻體在高爆轟作用下運動過程的整體模擬圖（時間跨度0.1～0.9 ms，間隔0.1 ms）Fig.5 The movement of a 3D vertical iron wall under the condition of a high-explosive detonation(the time span is0.1～ 0.9 ms,the interval time is0.1 ms)

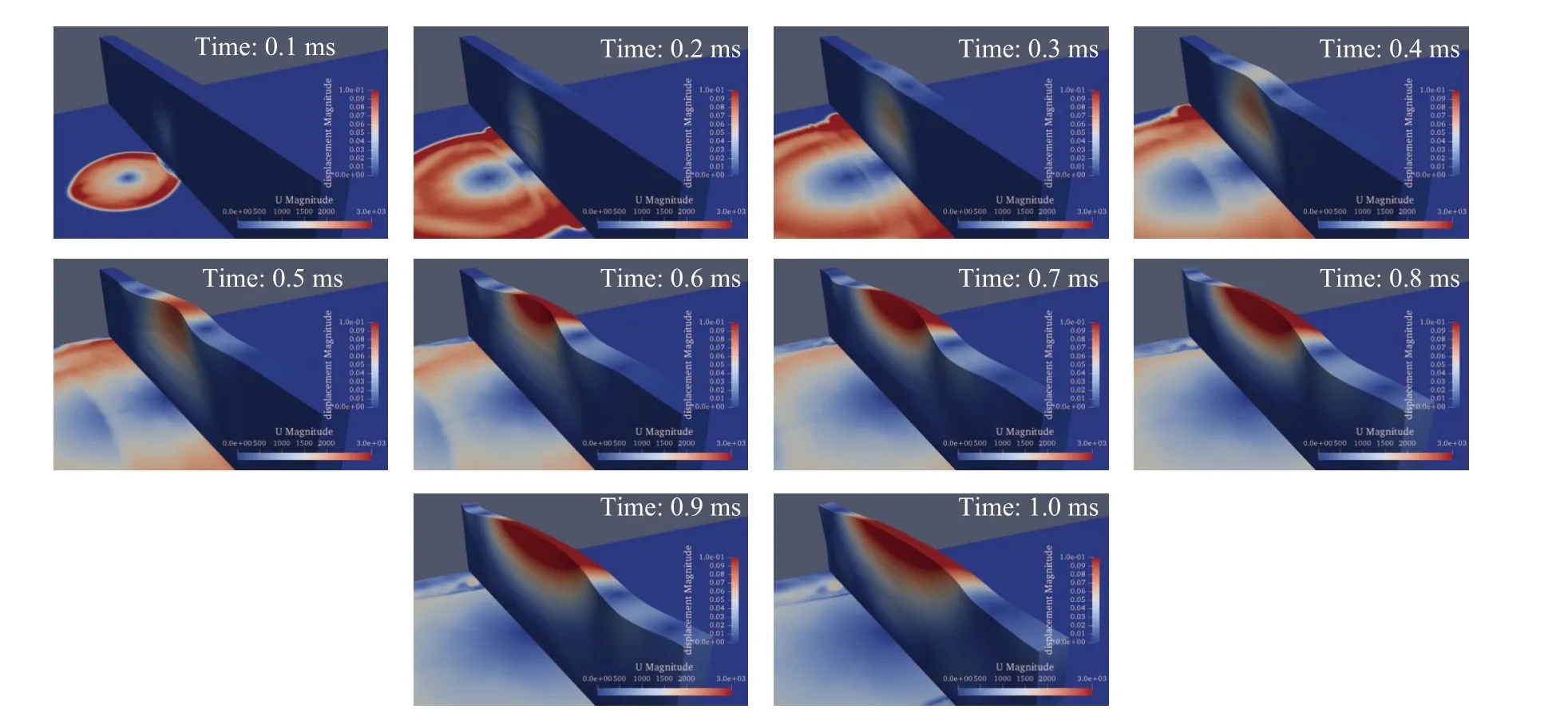
圖6 三維豎直混凝土墻體在高爆轟作用下的形變過程圖（時間跨度0.1～1.0 ms，間隔0.1 ms）Fig.6 The movement of a 3D vertical concretewall under the condition of a high-explosive detonation(the time span is0.1～ 1.0 ms,the interval time is0.1 ms)

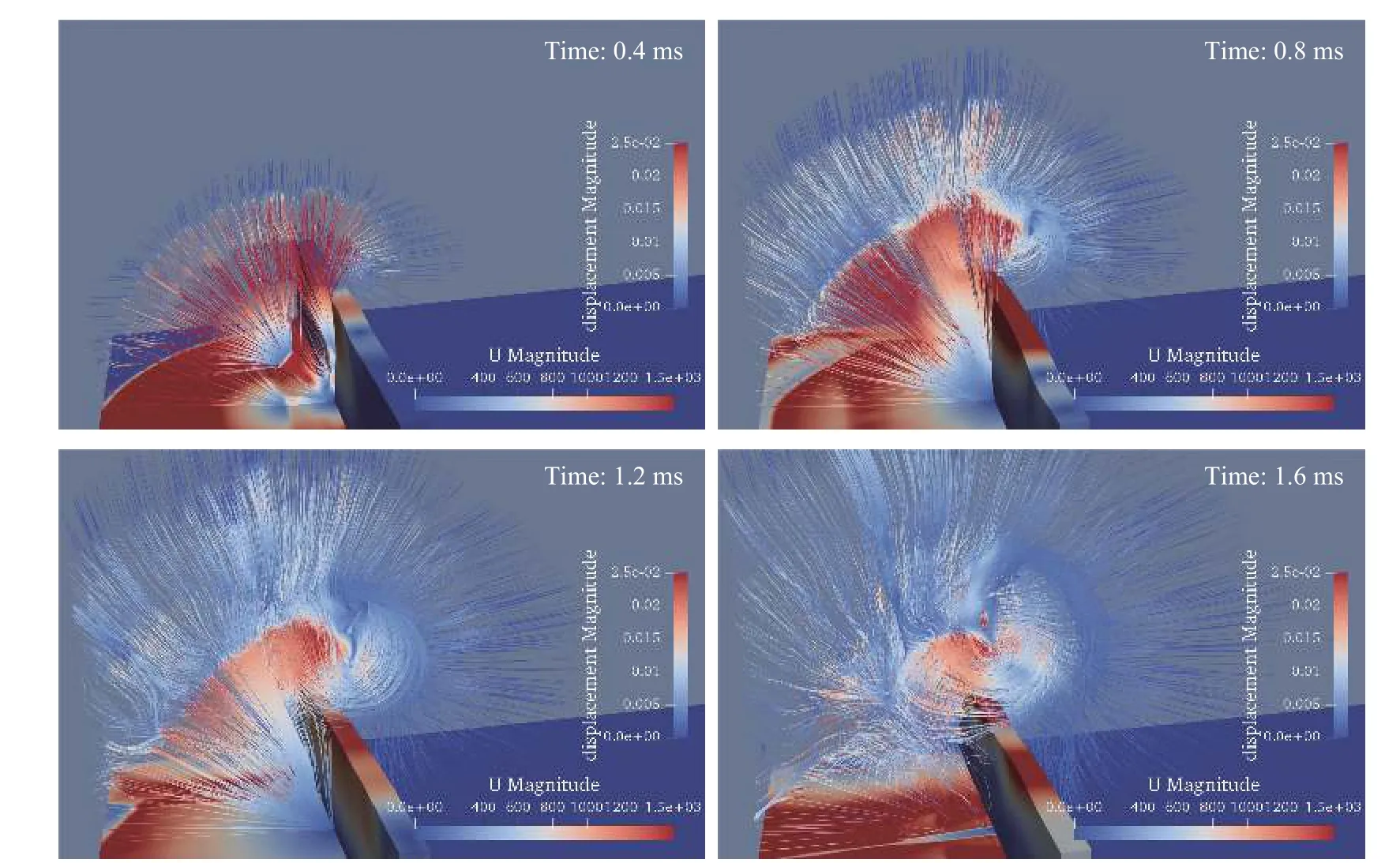
圖7 中截面后半部分在0.4、0.8 、1.2、1.6 ms的速度流線圖Fig.7 The velocity streamlinesin the second part of the central cross section at 0.4, 0.8 ,1.2,and 1.6 ms

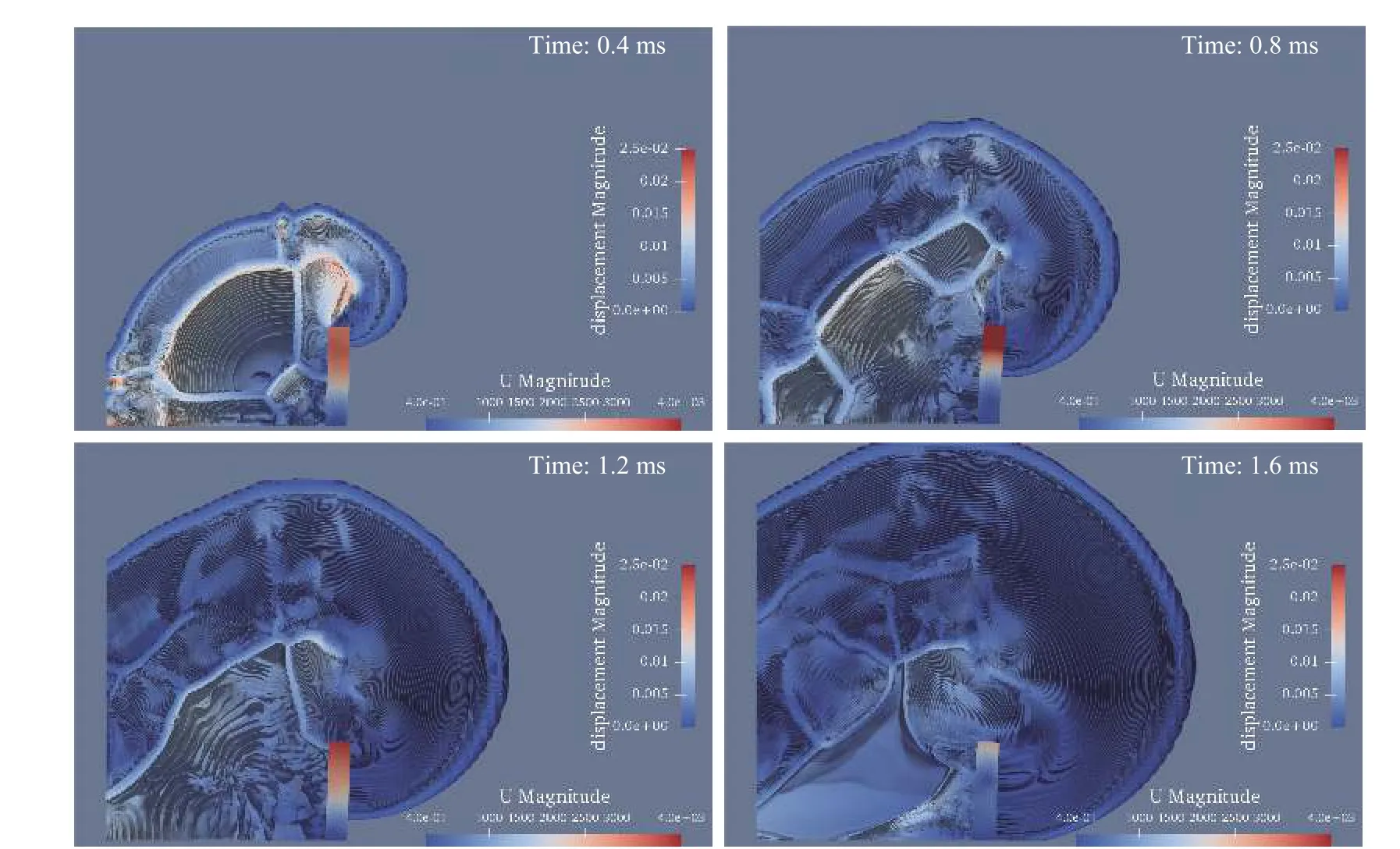
圖8 中截面后半部分在0.4、0.8 、1.2、1.6 ms的壓力等值線圖Fig.8 The pressure contours in the second part of the central crosssection at 0.4, 0.8, 1.2, and 1.6 ms

在0.8 ms時，爆轟波向外傳播，速度流線仍呈現向外輻射狀。此時渦旋已經非常明顯，同時呈現出梭形。在1.2 ms時，渦旋持續變大，流線出現混亂，不是規則的向外輻射狀。在1.6 ms時，流線的混亂程度變大。圖8和圖9顯示了中心橫截面后半部分的壓力等值線和密度等值線。可以看出，波面處的壓力和密度發生躍變，波面處的壓力和密度較高，而爆轟中心附近出現低壓和低密度區。

各采樣點處的壓力-時間和密度-時間歷程曲線如圖10和圖11所示。壓力和密度在爆轟波傳播到達的時候瞬間跳躍式增長，爆轟波傳播過后則迅速下降。通過壓力和密度變化的延遲情況可以判斷出爆轟波到達的順序。壓力和密度出現了多次增長，表示初始波和反彈波經過了采樣點。從圖中可以看出，爆轟波最先到達1號采樣點，壓力最高達1.61296×107Pa，密度最高達到25.9997 kg/m3。隨后到達2號、3號采樣點。其他采樣點處的密度最高到達5 kg/m3附近，之后不斷下降趨近于零。

圖9 中截面后半部分在0.4、0.8 、1.2、1.6 ms的密度等值線圖Fig.9 The density contoursin the second part of the central cross section at 0.4, 0.8 ,1.2,and 1.6 ms

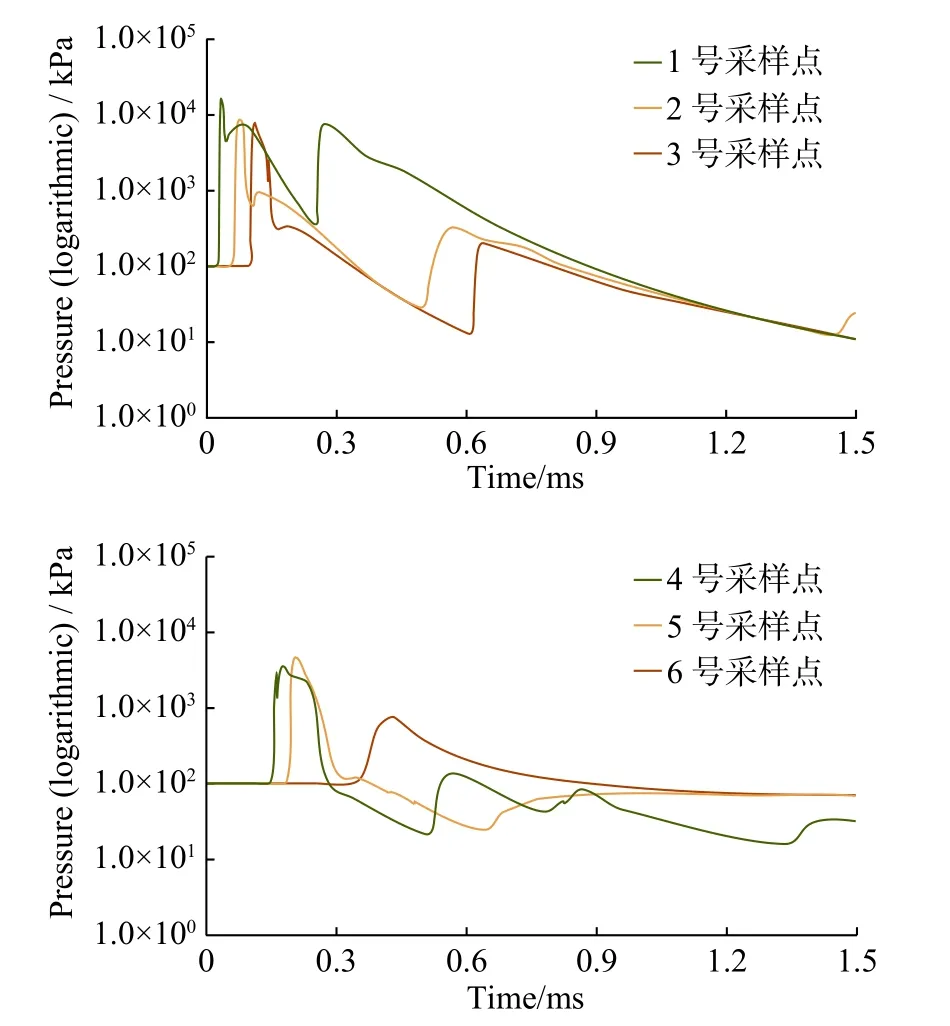
圖10 采樣點處的壓力-時間歷程曲線Fig.10 The time historiesof pressure

因為基于點對點通信模式和并行耦合格式，所以求解系統具有良好的并行可擴展性。我們設置了兩種不同規模的網格（網格1：流體300萬單元，固體10萬單元；網格2：流體500萬單元，固體10萬單元），分別采用串行顯式（方程（13））和并行顯式（方程（14））耦合格式展開測試。圖12顯示了網格1和網格2在串行顯式和并行顯式耦合格式下的時間開銷（400個時間步）和對應的加速比。對于同一網格，并行耦合格式的時間開銷相比于串行格式減少大約36%（網格1）和28%（網格2）。在256核四個測試的加速比達到最大，分別為122.3（網格1-串行耦合），141.2（網格1-并行耦合），147.0（網格2-串行耦合），178.0（網格1-并行耦合）。

圖11 采樣點處的密度-時間歷程曲線Fig.11 The time historiesof density

數值模擬給出了高能炸藥在三維豎直墻體后起爆并傳播的過程中各物理量的分布情況和高爆轟作用下豎直墻體的變形運動情況。模擬結果符合預期及爆轟過程的直觀印象，可為相關工程應用的數字化設計和評價提供技術支持。

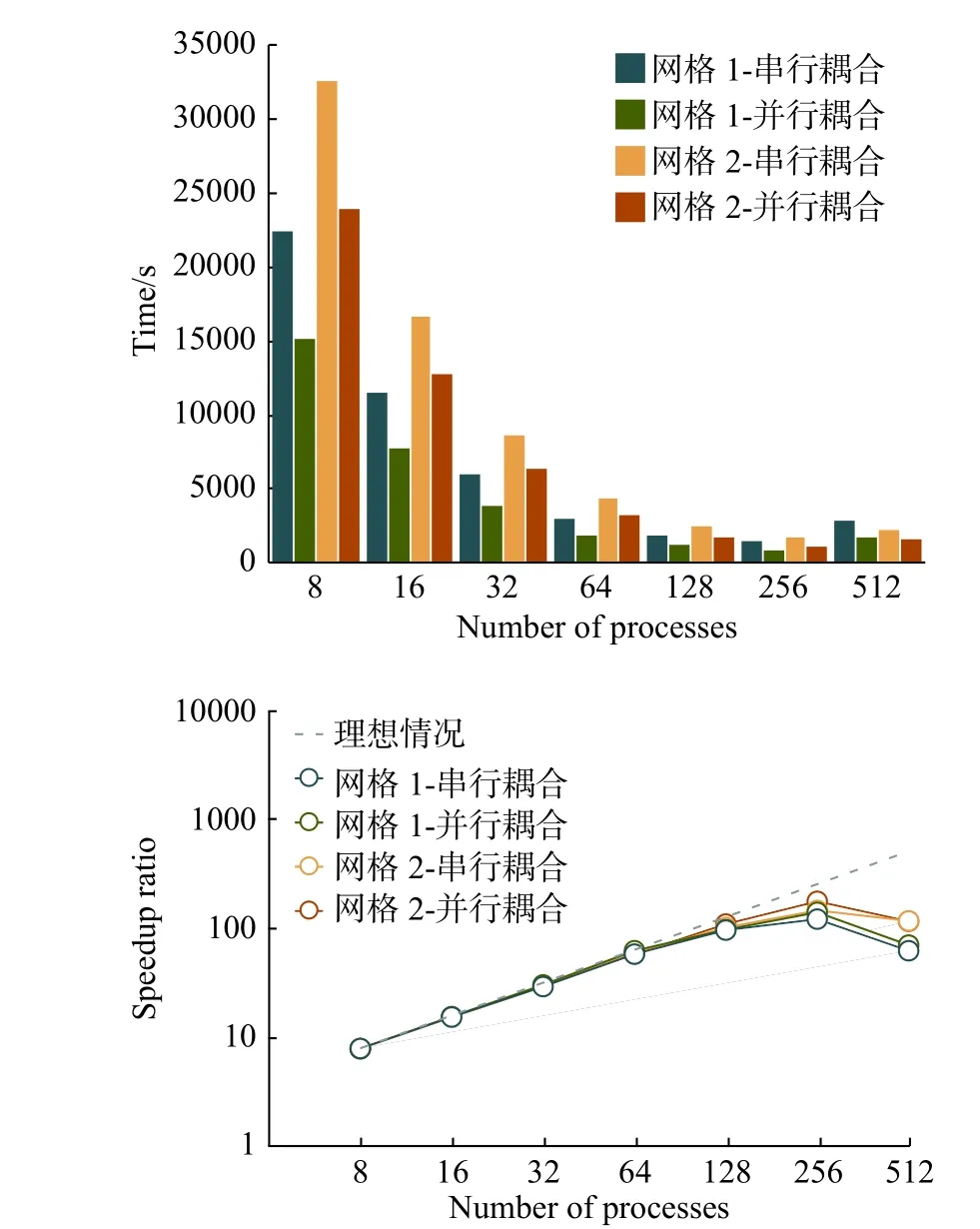
圖12 網格1和網格2在串行顯式和并行顯式耦合格式下的時間開銷（400個時間步）和對應的加速比Fig. 12 Thetime costs (400 time-steps) and the speedup ratios of Mesh1 and Mesh2 with serial-explicit and parallel-explicit coupling schemes

4 結論

爆轟沖擊作用下固體響應過程的研究在諸多工程應用中，如損傷評估、建筑爆破、礦物開采等，具有重要意義。然而，在復雜的工程應用中，準確高效地模擬爆轟沖擊作用下固體響應的過程存在許多困難和挑戰。

本文采用分離式流固耦合的方法，基于開源軟件OpenFOAM（blastFOAM）、preCICE和deal.Ⅱ實現數值模擬的求解系統，并利用三維豎直墻壁在高爆轟作用下的運動算例開展數值模擬。對于數值模擬結果，我們從爆轟響應整體過程、豎直墻體的形變過程、速度流線、壓力和密度等值線、采樣點處的壓力和密度變化等方面詳細展開分析。結果表明，該求解系統能夠準確有效地模擬爆轟波傳播的各個階段以及高爆轟作用下豎直墻體的變形運動情況，模擬結果展示的爆轟過程與Beyer報告中的爆轟波傳播過程一致。求解系統具有良好的并行可擴展性，在并行度為256核時的加速比達到141.2和178.0，并行效率分別達到55.2%和69.5%。總而言之，本文通過集成開放源代碼，實現了面向爆轟沖擊的分離式流固耦合數值模擬求解系統，該系統在諸多領域的工程應用中都具有重要的現實意義。