列車空調出風口導流板高度對冷凝風量影響研究

李雪亮，伍 釩，王田天，陶 羽，徐任澤

(1.中國空氣動力研究與發展中心空氣動力學國家重點實驗室，綿陽 621000；2.中南大學交通運輸工程學院，長沙 410075；3.軌道交通安全關鍵技術國際合作聯合實驗室，長沙 410075)

0 引言

高速列車的舒適性一直是列車空氣動力學的熱點問題之一，而空調系統則是列車上用于保障旅客舒適性的重要組件。空調系統能否正常工作，是關系到高速列車舒適性的核心問題。

空調冷凝風機的作用是為冷凝器提供冷凝風，以主動散熱的方式加速冷凝器與外界環境的熱交換效率[1-3]。空調散熱所需冷凝風量較大，通常使用軸流風機以提供足夠的風量，其缺點是對環境壓力變化敏感，抗壓力逆差能力弱。

高速列車運行過程中，車身周圍流場環境（溫度、壓力、流速等）不斷隨車速而變化，車身不同位置的流動結構也存在較大差異[4-7]，這會對空調內外的流場結構產生顯著影響。而由于冷凝風機對環境壓力變化的敏感性，列車運行過程中空調冷凝風量會出現較大波動，直接影響了空調系統的散熱效率。空調系統冷凝風量減少，會導致冷凝器溫度升高，帶來制冷功率下降甚至空調報警停機的危害。

目前國內外研究主要是直接通過列車表面壓力分布，研究空調冷凝風量隨車速的變化規律[8-9]，各文獻均指出冷凝風量會隨車速快速下降。文獻[10]指出，導致冷凝風量下降的主要原因有以下兩個方面：1）進風口處，橫向柵格受列車運行產生的高速氣流作用產生負壓區域，阻礙空調吸氣；2）出風口處，冷凝風與列車運行產生的高速氣流相互作用，在出風口上方形成正壓區域，阻礙空調排氣。

由于高車速下空調冷凝風量的較大降幅將直接危害到空調系統的正常運行，所以需要針對列車運行時的空調冷凝風量進行優化研究。目前有關優化措施的研究相對較少。針對這一問題，本文從改善空調出風口壓力環境入手，在空調冷凝出口外側使用鍥狀導流板，擬通過降低出風口側壓力，達到增加冷凝風量的目的。本文基于三維非定常不可壓縮雷諾時均N-S方程，采用k-ε湍流模型和DDES方法，通過構建帶有空調系統的列車整車空氣動力學計算模型，對運行中的高速列車及空調系統進行數值模擬，研究不同導流板高度對緩解冷凝風量下降的效果差異。

1 計算模型

1.1 湍流模型和數值計算方法

計算中雷諾數為Re =2.70×107，這表明本文研究中列車周圍的流場處于強湍流狀態。列車周圍流場，尤其是空調進出風口附近和空調內部，旋渦脈動劇烈（如圖1所示）。采用RANS方法難以準確模擬旋渦脈動，這將導致計算結果精度較低[10]。分離渦（DES）方法[11]能夠捕獲渦脈動特征，可以保證足夠的計算精度，且計算量遠小于LES方法，因此在解決高雷諾數、大規模分離流的問題時具有較大優勢[12]。目前，DES方法已用于多種條件下的高速列車外部流動研究，并得到了較好的計算結果[13-17]。延遲分離渦（DDES）是DES的改進方法，可以減小DES方法中存在的網格誘導分離與渦黏系數衰減問題[18]。本文選擇使用基于Realizable k-ε湍流模型的DDES方法模擬湍流流動，對流向的差分格式采用具有二階精度的QUICK格式，速度-壓力耦合求解方法為壓力修正法的改進方法SIMPLEC算法。

圖1 列車及空調周圍流場特征Fig. 1 Characteristics of the flow field around the high-speed train and the air-conditioning unit

1.2 列車模型

本文使用如圖2所示的高速列車模型進行仿真計算。高速列車附有外形較為復雜的附加設備，而本文的研究重點為列車頂部空調系統冷凝腔，模擬車體附加設備會大幅度增加模型生成和計算域離散的難度，增大計算量。為節省資源，參考EN 14067標準[20]的要求，對列車進行了適當簡化，將車體除空調外的所有復雜結構作光順化處理，忽略轉向架、受電弓、風擋等設備及部件。

圖2 高速列車模型Fig. 2 High-speed train model

計算使用的列車為3車編組，去掉轉向架后的車高Htr×車長Ltr×車寬Wtr為4.05 m×81 m×3.38 m，頭部流線型長度為12 m。空調位于頭、尾車，空調中心位置距列車鼻尖點為23 m，其中，頭車上的空調由AC1表示，尾車上的空調由AC2表示。

1.3 空調模型

本文使用單元式空調進行研究，空調由蒸發腔、冷凝腔、廢排裝置三個獨立的部分組成（各部分之間由隔板隔開，相互之間沒有氣流通道）。空調的散熱能力主要取決于冷凝腔的排熱效率，又因為空調系統各個部分相互獨立，所以可以將其余部分進行簡化，只保留冷凝腔，得到計算模型如圖3所示。空調內部的氣流流向為冷凝風由風機吸入冷凝腔，通過冷凝器進行熱交換，最后通過冷凝出口格柵排出。空調長寬高為LAC×WAC× HAC=1.6 m×1.8 m×0.5 m；出風口長寬為1.459 m×0.265 m；進風口長寬均為0.596 m；冷凝器長寬為1.480 m×0.434 m；風機葉片直徑為557 mm，風機軸為圓柱形，直徑199 mm。

圖3 高速列車空調冷凝腔模型Fig.3 Condensing chamber of the air conditioner on high-speed trains

空調模型中，冷凝風機和冷凝器兩個部分較為復雜，難以直接模擬。冷凝風機為復雜曲面外形的軸流風機，本文使用風機面邊界條件簡化模型，仿真中輸入的風機性能曲線如圖4所示。圖中曲線為通過風機所在平面時，平面兩側壓力差與流速的關系曲線。冷凝器為具有極小幾何尺寸的翅片結構，本文利用多孔介質模型代替，取黏性阻力系數=4.78×107/m2，慣性阻力系數C2= 1306/m。

1.4 導流板布局方式和形狀參數

導流板結構通過揚起出風口前端的高速氣流，使出風口上方氣流速度降低，同時在出風口上方形成負壓區域，降低空調出風口側壓力，減小流動阻力，以達到緩解風量下降的目的。針對高速列車雙向行駛的需求，本文提出的導流板結構為對稱布局，與車頂表面貼合，如圖5中D1～D4所示。

圖4 風機性能曲線Fig.4 Performance curve of the condensation fan

圖5 導流板結構在列車頂部的結構示意圖Fig.5 Schematic of deflectorson the roof of train

由文獻[10]可知，導流板結構可以在空調出風口上方產生負壓區，從而達到緩解冷凝風量隨車速下降的目的。導流板高度會影響負壓區域的強度，是決定冷凝風量的關鍵因素之一。本文分別建立Hd=30、45、60 mm三種 導 流 板高 度。對車 速V =350 km/h時，不同高度導流板對空調冷凝風量的影響展開研究。三種導流板的具體尺寸參數如圖6所示。

圖6 不同高度導流板示意圖（單位：mm）Fig.6 Schematic of deflectors with different heights(unit:mm)

1.5 計算域和邊界條件

為確保列車周圍的流場得到充分發展，邊界不會對流場計算結果產生干擾，需要設置足夠大的計算域。根據EN 14067標準[20]的要求，本文設置的計算域和邊界條件如圖7所示，所有尺寸均通過車高H =4.05 m進行無量綱化。計算域總長為65H，其中列車前部長度為10H，后部長度為35H，列車長度為20H，計算域寬為18H，高為14H。采用相對運動的方式模擬列車運動，即列車靜止，空氣和地面以速度V向列車運動。設置空氣以速度V向x正方向自速度入口流入，根據文獻[21]中的參數，入口流動參數湍流強度取1%，湍流黏性率取10；流動出口為壓力出口，出口處相對壓力設為0；為模擬與列車的相對運動，地面設置為無滑移壁面，并以速度V向x正方向運動；計算域頂部和側面采用靜止無滑移壁面。

圖7 計算域與邊界條件設置Fig.7 Computational domain and boundary condition setup

1.6 計算網格

本文使用混合網格方法離散計算域。以空調格柵為界，由于內部結構復雜，內部流動方向難以預測，格柵下方的空調腔使用非結構四面體網格離散；計算域的其余部分使用結構化六面體網格進行離散，以保證列車附近的流場獲得較好的計算精度[22]。

y+為無量綱的壁面距離，用來衡量壁面法向網格尺度對湍流模型的適應性。本文所使用的Realizable k-ε模型要求y+＜300，此處取目標y+=250可得預估的車體表面第一層網格厚度為Δs =1.12×10-3m，本文將Δs向下取整為Δs = 1 mm。網格細節由圖8給出。

圖8 計算網格Fig.8 Computational grid

1.7 計算設置和數據處理方法

在本文研究中，所有計算均使用ANSYS Fluent的壓力基求解器進行非定常求解，計算時間步長取Δt = 0.001 s，每時間步方程的各項殘差均低于1×10-3。

為便于對比分析，風量系數Cq和阻力系數Cd通過式（1）、式（2）定義：

式中：Q為計算得到的空調風量；Q0=14222 m3/h為列車靜止時由試驗測得的空調風量；D為阻力；ρ為空氣密度，取1.225 kg/m3；V∞為無窮遠處來流速度；參考面積S = 13.4 m2為列車非流線型處的橫截面積。

本文研究中，使用無量綱時間Tref對流場時間進行衡量[19,23-24]：

式中，t為計算時間，Htr為車高4.05 m。計算總時長為192Tref。

圖9為列車兩個空調AC1和AC2的風量系數Cq隨計算時間的波動特征。可以看出，各監測量隨時間無規律波動，在時間t≥50Tref后，波動趨于平穩且具有周期性。這意味著流動已充分發展，流場趨于穩定。因此本文所有測量數據，如阻力、壓力、風量等，均取無量綱時間[50Tref,192Tref]內的平均值作分析。

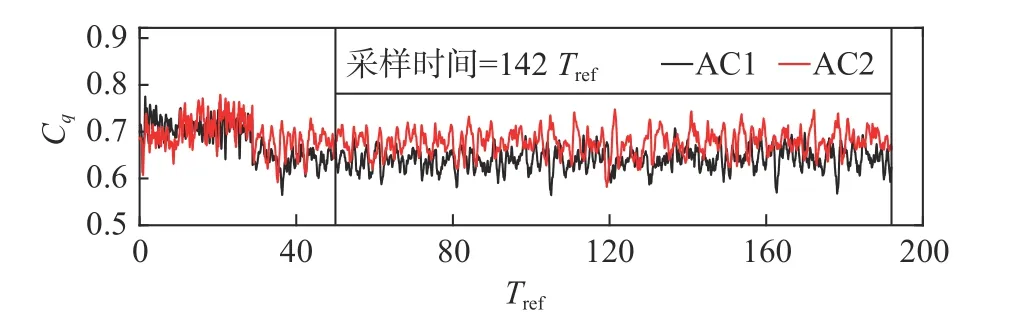
圖9 監測數據隨時間波動曲線Fig.9 Time variation of the monitoring data Cq

2 計算驗證

在數值計算中，所使用的離散網格對計算精度起著決定性作用。本文采用粗、中、細三種網格研究網格密度對計算結果的影響，以確保網格密度與計算資源匹配。由前文可知，計算網格的第一層網格厚度可以滿足湍流模型需求，因此，在保證三種網格的車體表面第一層網格厚度均為1 mm的條件下，通過調整網格尺度和增長率，分別建立三種計算網格，具體網格參數見表1。

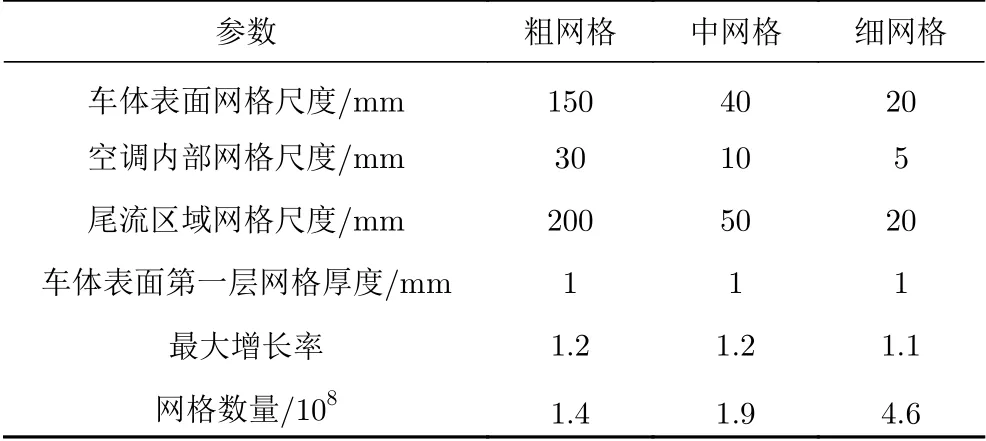
表1 不同計算網格尺度Table 1 Scalesof different grid sizes

基于前文所述計算方法，列車靜止情況下計算得到的三種網格精度的空調冷凝風量結果如表2所示，并與文獻[10]中列車靜止狀態下試驗測量所得的冷凝風量進行對比。可以看出，粗網格與試驗相比誤差最大，為7.45%；中等網格誤差為2.57%；細網格誤差為1.20%。粗網格雖然網格數量較少，計算資源消耗小，但是誤差較大，精度不高；細網格得到的計算結果最好，然而網格數量過大，現有計算資源難以支撐本文的全部計算；中網格具有與細網格相似的計算精度，而計算資源消耗遠小于細網格。因此，本文所有計算均基于中網格開展。

表2 不同網格尺度與試驗結果對比Table 2 Comparison between theair flux computed with different grid sizes and the experiment result

3 導流板高度對冷凝風量影響分析

3.1 冷凝風量變化規律

圖10展示了不同導流板高度下冷凝風量的變化趨勢。可以看出，隨著導流板高度增加，風量逐漸增大，緩解風量隨列車運行而下降的效果更加明顯。未使用導流板時，兩空調平均風量系數僅為0.453，而使用高度為Hd=60 mm的導流板后，平均風量系數達到0.791，相對增加74.6%，效果十分顯著。但導流板高度增加，也會帶來風量系數標準差增大的問題，意味著空調風量波動幅度增大，而較大的風量波動幅度可能會影響空調使用壽命，產生風機偏振等問題。

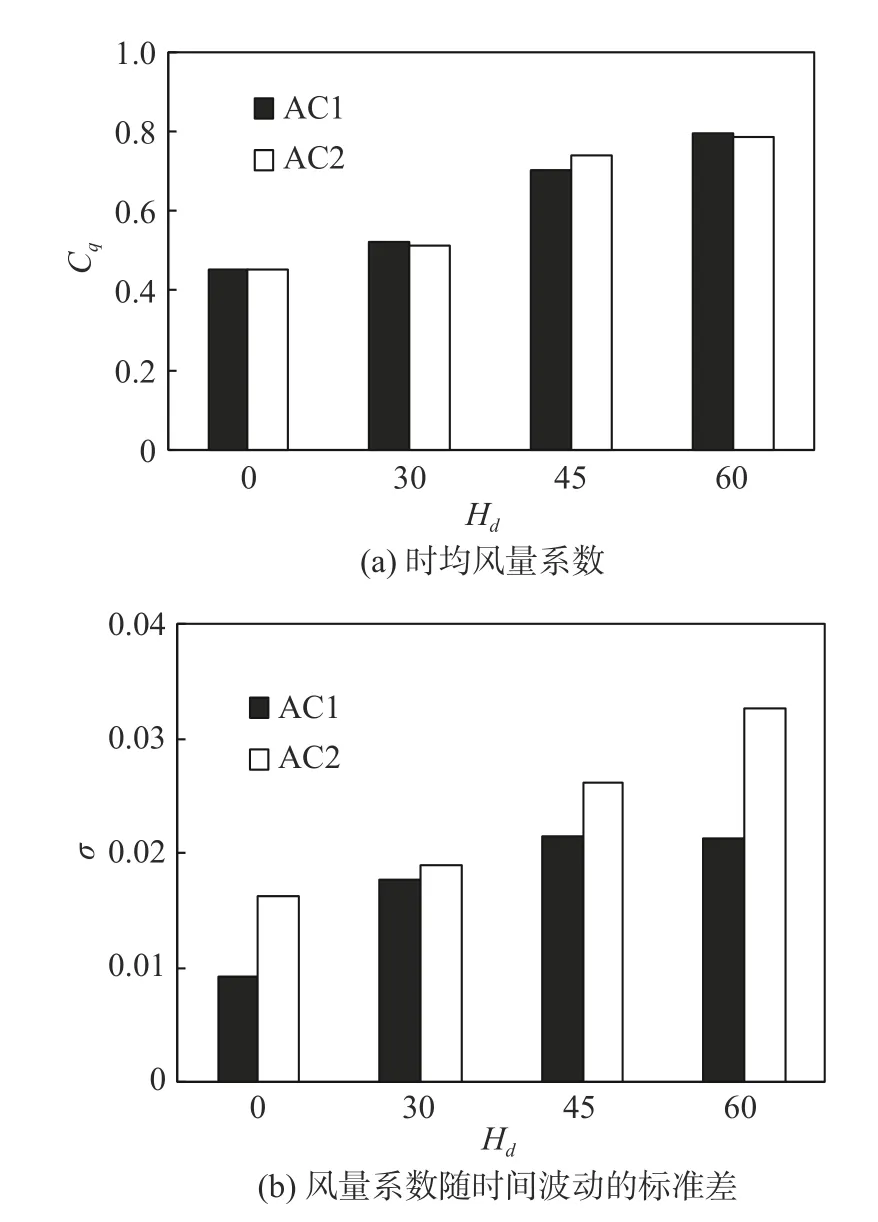
圖10導流板高度對冷凝風量影響Fig.10 Influence of the deflector height on the condensing air flux

3.2 導流板高度對阻力影響分析

圖11 給出了導流板高度對整車阻力的影響。由于列車模型簡化程度較高，整車阻力系數較低，但計算結果足以體現出空調和導流板對阻力的影響。圖中Cd1為車身阻力；Cd2為扣除Cd3后空調受到的總阻力；Cd3是高速來流作為冷凝風被吸入空調腔時，氣流動量變化所帶來的不可避免的阻力增量，由式（4）代入式（2）推導得到：

Cd4為兩個空調8塊導流板所受到的總阻力。

圖11 不同導流板高度對整車阻力影響Fig.11 Influenceof the deflector height on the drag of high-speed trains

由圖11可知，不同工況下Cd1和Cd2基本不變。Cd3由式（4）可知與風量成正比，是風量增加所帶來的不可避免的阻力增量。而Cd4則隨導流板高度增加快速上漲。結合冷凝風量來看，采用Hd= 45 mm的導流板是兼顧風量與阻力的較優選擇。同時可知，對于高速列車的數值計算，是否考慮空調阻力會對總阻力帶來3%左右的差異。

3.3 流動隨導流板形狀變化特征分析

圖12給出了空調附近區域的壓力云圖。可以看出，無導流板情況，出風口正上方有較小的正壓，但由于軸流風機對壓力的敏感性，該正壓會對空氣流動產生較大阻礙，導致風量出現較大幅度下降。導流板高度為Hd=30 mm時，出風口正上方處于較弱負壓區內，對風量有一定增長作用。隨著導流板高度進一步增加，負壓逐漸增強，對空調風量隨車速下降的緩解作用也逐漸增強。

圖13給出了剖切面上的速度云圖與流線圖。圖中以無窮遠來流速度V∞對速度進行了無量綱化。從圖中可以看出，導流板高度為Hd=0和Hd=30 mm兩個工況，冷凝風均直接從出風口處流出，但由于流動阻力較大，流量相對較小。Hd= 45 mm和Hd= 60 mm時，列車外部的高速氣流撞擊在出風口后部的導流板上，導致氣流在出風口末端出現回流，一定程度上削弱了導流板的優化作用。但由于導流板引起的負壓強度較大，風量仍有一定程度增加。

圖12 空調冷凝出口處時均壓力云圖Fig.12 Time-averaged pressure contours at the condensing outlet of the air conditioner

圖13空調冷凝出口處時均速度云圖及流線圖Fig.13 Time-averaged velocity contoursand streamlines at the condensing outlet of theair conditioner

圖14 為不同導流板高度下的附面層曲線。當車頂無空調時，附面層以近似于平板流動的形式發展，沿車長方向緩慢增厚。有空調的情況下，空調對前方的附面層厚度影響不大，而空調后部附面層由于混入空調冷凝風而被揚起。在空調前方增加Hd= 30 mm的導流板后，附面層受導流板影響而被揚起，但由于導流板所處的高度流速低，變化幅度較小。隨著導流板高度進一步增加，對附面層的影響變得顯著。Hd=45 mm與Hd=60 mm的導流板對附面層影響相似，附面層先被揚起至較高高度，隨后受空調冷凝出口負壓影響，高度迅速下降。在混合冷凝風之后，由于冷凝風量較大，低速氣體占比相對于其他工況更多，附面層厚度增加更快。

圖14空調冷凝出口處時均附面層曲線（0.99V等值線）Fig.14 Time-averaged boundary-layer thickness (iso-linesof 0.99V)at the condensing outlet of the air conditioner

3.4 渦結構演變規律分析

圖15為AC1外部的Qcriteria= 30000/s2等值面圖，并通過時間平均速度進行著色。無空調的車身，由于車體表面光滑，Qcriteria= 30000/s2時無法觀察到明顯的渦結構產生，故此處將無空調工況的Qcriteria等值面圖略去。對于有空調的研究工況，導流板高度的差異，會對空調冷凝出口渦結構產生較大影響。由于空調的吸氣作用和格柵影響，進風口處的渦細碎且與格柵貼合較緊。隨著導流板高度增加，空調風量增大，吸氣作用更加強烈，進風口處渦結構與格柵貼合更加緊密。處于排氣一側的出風口處湍流流動相對較為強烈，渦的尺寸隨著流動的發展而增加，導流板較高時這一現象更加明顯。無導流板時，冷凝出口處渦較小且破碎，這是由于冷凝風量較小且車體附近空氣流速較快造成的，空調排出的冷凝風被強烈的列車運行產生的高速氣流快速稀釋，在較短的空間范圍內被耗散。導流板高度為Hd= 30 mm時，渦脫尺度顯著增大，可以看到相對無導流板工況，“發卡”狀的較大渦結構數量和尺寸均明顯增加。隨著導流板高度進一步增大，渦在寬度和高度方向均發展更快，渦脫尺度也明顯進一步增大。

圖16顯示了空調處5個截面x1～x5的時均流線圖。圖中，渦結構尺寸、渦心位置均清晰可見。x1截面包含了空調內部的流動渦結構，無導流板情況下，空調內部存在兩個大渦，分別位于左右兩側；而隨著導流板高度增加，空調內部趨于均勻流動。x2～x5位于空調后方，可以看出，渦的尺度隨導流板高度增加而增加。氣流剛流過空調出風口時，在x2、x3截面，流動相對紊亂，具有眾多小渦結構，而氣流到達x5截面時，最終都會趨于形成4個對稱的大渦結構。

圖15 空調外部瞬態渦結構（Q criteria =30000/s2，由時均速度著色）Fig.15 Instantaneous vortex structures (iso-surface of Q criteria =30000/s2,colored by the time-averaged velocity)at the outlet of the air conditioner

圖16 截面x1-x5上的時均流線圖Fig.16 Time-averaged streamlinesat the crosssections x1-x5

4 結論

本文通過對不同導流板高度下列車空調冷凝風量的仿真研究，得到以下結論：

不使用導流板優化措施時，冷凝風量下降量在車速V =350 km/h時可達54.7%。在出風口外側安裝導流板可以較大程度緩解冷凝風量隨車速快速下降的問題。出風口外側的導流板結構通過改變出風口處流動結構，揚起車側的高速氣流形成負壓區，達到緩解風量下降的目的。

隨著導流板高度增加，冷凝風量隨車速下降幅度減緩，但波動更加劇烈。Hd= 30 mm的導流板阻力較小，對流場影響較小，緩解風量下降的效果也較弱。Hd=45 mm和Hd=60 mm的導流板可以有效緩解風量隨車速下降的問題，兩者風量較為接近，但Hd=60 mm的導流板帶來的阻力較大。車速V =350 km/h時，導流板高度分別為Hd= 30、45、60 mm時的冷凝風量分別下降48.5%、29.8%、21.3%，而阻力系數分別為0.2716、0.2767、0.2809。綜合考慮可知，Hd= 45 mm的導流板是緩解冷凝風量隨車速快速下降的較優措施。