橫流駐波增長因子模式在跨聲速邊界層的應用

王玉軒，徐家寬，*，張 揚，喬 磊，白俊強，3

(1.西北工業大學航空學院，西安 710072；2.西安交通大學機械結構強度與振動國家重點實驗室，西安 710049；3.西北工業大學無人系統技術研究院，西安 710072)

0 引言

以減阻、減排為核心的“綠色航空，清潔藍天”計劃的提出使得層流設計和層流控制技術成為全球的研究熱點。要進行層流設計和控制技術研究，轉捩預測技術是首當其沖需要解決的難題[1]。

經過近半個世紀的研究和諸多知名研究機構關于亞跨聲速邊界層轉捩預測的研究和實踐，基于線性穩定性理論（linear stability theory,LST）的eN方法表現突出。eN方法是一種半經驗的轉捩預測方法，一般通過線性穩定性理論求解得到不穩定波的增長因子N在空間的分布，人為給出轉捩臨界N值，從而獲得轉捩位置。Klebanoff等[2]的研究表明小擾動環境下，邊界層內擾動的T-S波線性演化區域幾乎占據轉捩前整個層流區域的80%左右，盡管橫流波到非線性階段飽和區域較長，但是其線性發展區域仍然占大部分區域，這是使用線性穩定性理論預測T-S波轉捩和橫流轉捩能夠成功的根基。二維邊界層的eN方法于20世紀50年代被Smith[3]和Van Ingen[4]提出，在航空航天領域得到了廣泛應用。該方法后來被Mack[5]和Cebeci[6]等進一步拓展至三維邊界層，使得基于LST的eN方法在理論分析層面趨于完善。為了使得eN方法能夠計算部分工程問題，國內外的眾多知名科研機構都發展了基于傳統線性穩定性理論的eN分析程序[7-10]，與CFD求解器和邊界層方程等外部求解器耦合迭代從而實現線性穩定性分析。法國宇航研究中心（ONERA）[11]和德國宇航研究中心（DLR）的科研人員[12]基于多年的穩定性分析數據構造了基于線性穩定性理論的eN數據庫，將該數據庫與CFD求解器和邊界層方程等外部求解器一起耦合求解，從而獲得所需要的擾動增長因子N。

傳統的基于線性穩定性理論的標準eN方法包括以下六個步驟：第一，求解精確的層流基本流；第二，對層流基本流進行速度分解和坐標變換以及法向一階導數和二階導數的計算；第三，猜測不穩定波可能出現的區域和參數區間，通過求解擾動波的特征值篩選不穩定波；第四，沿流線方向積分特征值獲得不同擾動的增長因子（N factor）；第五，給定臨界N值判定轉捩位置；第六，通過固定轉捩的方式給出層流區和湍流區的分布，從而計算氣動力。

經過國內外知名科研機構的驗證，基于線性穩定性理論的eN方法可以對工程中出現的常規氣動外形表面的Tollmien-Schlichting（T-S）波轉捩、層流分離泡轉捩和橫流不穩定性轉捩進行預測，滿足工程需求。這種RANS求解器與eN求解模塊的迭代耦合策略在一定程度上將傳統的線性穩定性理論分析推廣到了比平板、翼型更為復雜的常規氣動外形，在機翼、翼身組合體、升力體等構型的轉捩預測中得到了廣泛應用[13-14]，可以解決大部分工程問題，理論上該方法適用于任意復雜外形的轉捩預測。但是，該方法實現難度較高，前后處理較為復雜。存在以下問題：第一是分析過程比較復雜，即使是數據庫方法，也需要獨立的轉捩分析模塊去單獨處理線性穩定性理論的求解，然后與RANS求解器進行耦合迭代。該方法各模塊的代碼之間耦合性較差、復雜度高，且在并行化計算方面較難實現。對于稍微復雜的基本流求解和速度分解等都很難保證求解精度，依然需要進行積分和搜索等非當地操作，不符合RANS模式僅依賴當地變量的發展需求。第二是只能給出局部規則區域的層流-湍流分布，難以給出復雜氣動外形的全機層流-湍流氣動力數據，這對層流優化設計而言是非常難以接受的。第三個是對于擾動源的考慮不足，對于壁面粗糙度的影響，需要通過改變橫流駐波轉捩臨界N值的方法加以考慮。Crouch等[15]發展的臨界N值判定準則尚不具備普適性，僅由一組試驗數據標定而來。

隨著近年來基于RANS方程的當地化轉捩模式的快速發展[16-28]，結合兩者的優點，讓線性穩定性理論模式化的思路逐漸涌現。1982年，Drela和Giles[29]對不同壓力梯度下的層流相似性解進行了大量的線性穩定性分析，從而獲得了T-S波的擾動增長因子N與形狀因子和動量厚度雷諾數的直接函數映射關系。這是研究人員首次對線性穩定性理論進行簡化，使得eN方法可以非常便捷地應用到翼型繞流的轉捩判定當中。2013年開始，Coder和Maughmer[30]基于Drela等[29]的研究成果，首次提出了流向擾動增長因子NTS的輸運模式。該模式的構造思想為：對不同壓力梯度下的邊界層相似速度型進行大量的變參數穩定性分析，從而提煉出N值包絡線與當地形狀因子和動量厚度雷諾數以及邊界層特征尺度之間的函數映射關系；然后對關系式中出現的非當地變量逐一進行合理的當地化，提出新的流場識別因子，構造新的計算函數，最后與湍流模式耦合形成轉捩-湍流預測模式。模式構造完成后應用非常簡單便捷，與CFD求解器求解基本流一起計算，一次性求解即可獲得整個氣動構型的層流-湍流分布和整體的氣動力等數據。隨后，Coder不斷對該模式進行改進，尤其是提出了滿足伽利略不變性的形狀因子參數[31]，使得該模式在非慣性坐標系下也不再有缺陷，整體預測性能趨于完善。但是該模式只能預測流向的T-S波轉捩和層流分離泡轉捩，無法對橫流轉捩進行預測。而航空航天飛行器表面，橫流轉捩現象非常突出。Coder等[32]在2020年對該方法進行了發展，將橫流判據加入其中，使得該方法能夠用于橫流轉捩的預測。但是，其對于橫流的預測，采用的是Langtry等[18]通過風洞試驗數據擬合出的經驗關系式，沒有對橫流不穩定波的發展進行獨立的、物理的建模。低湍流度環境被認為與高空實際飛行環境相似，在此環境下，盡管非定常橫流渦的增長率更大，但是三維橫流邊界層流動主要由定常橫流渦主導轉捩[33]。因此，對于小擾動飛行環境，后掠翼表面橫流定常波的分析和建模是關注的重點。為了完善這一功能，Xu等[34-35]提出了橫流定常波擾動增長因子NCF輸運模式，以橫流強度因子和螺旋度雷諾數為根基發展了完全基于當地變量的NCF輸運模式，經過廣泛的低速算例驗證，證實了其合理性。隨后，該模式又進一步被添加了壁面溫度效應修正[36]，使其可以對跨聲速的部分變壁面溫度算例進行預測。

本文將重點展示當地化的NCF輸運模式在跨聲速后掠翼流動中的公式細節和應用實例，驗證其在跨聲速邊界層中對橫流駐波擾動增長因子的預測能力，證實其合理性和可行性，進一步促進該方法的推廣應用。對于eN方法與轉捩經驗關系模式的預測結果比較，可以參考文獻[37，38]。

1 輸運方程的數學描述

在包絡近似方法中，唯一需要追蹤的變量就是沿流動方向發展的包絡增長因子N。Drela等[29]的簡化模式的線性穩定性理論可使用增長因子標量輸運方程來實現流場中增長因子N的求解。Coder等[30]首先通過無量綱化的當地壓力梯度參數 HL=實現非當地形狀因子H12的當地化計算，從而實現了整個輸運方程內核公式的當地化求解。這里S是剪切應變率的模，d為流場中任意一點到壁面的最小距離，Ue是邊界層邊緣速度。Coder等[30]構造的Tollmien-Schlichting （T-S）不穩定波增長因子輸運模式的形式為：

其中，擴散項系數σn,TS=1.0， Pn,TS是源項，μ是分子運動黏度系數，μt是湍流渦流黏度系數。源項是基于Drela的LST分析結果進行建模，所用到的失穩雷諾數和N因子增長斜率函數等均是流向形狀因子H12的函數，具體公式信息可以參考文獻[30]。

上述模式只能對流向轉捩（T-S波和層流分離泡轉捩）進行預測，無法預測橫流轉捩。本文作者基于對三維層流邊界層相似性解進行的大量的線性穩定性分析結果，提出了橫流駐波的擾動增長因子輸運模式：

其中，擴散項系數σn,CF等于1.0，源項Pn,CF由以下幾個部分組成：

式中，ρ是密度， Fonset是開關函數， NCF_growth是增長因子的發展函數和TCF是可壓縮修正項目。所有函數的構造都源于對不同壓力梯度和后掠角（0°～90°）下的Falkner-Skan-Cooke三維層流邊界層相似性解進行的線性穩定性分析結果。

第一，開關函數的表達式為：

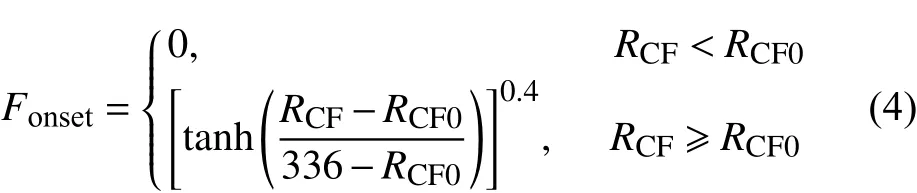
根據穩定性理論分析結果，起始失穩橫流雷諾數RCF0是 橫流形狀因子 Hshape=的函數，計算公式為：

這里，Tw是壁溫，Te是邊界層邊緣的溫度。在 Hshape的定義中，dmax是 最大橫流速度的高度，δCF（等于到橫流速度分量變為其最大值的10%時與壁面的距離，靠近邊界層邊緣一側的值）是橫流特征厚度。橫流雷諾數RCF定義為RCF=|wmax|，|wmax|是最大橫流速度的絕對值，υe是邊界層邊緣的運動黏度。

關于橫流雷諾數RCF的當地化，我們提出了一個新的當地指示因子該指示因子的定義不同于Grabe等[17]發展的螺旋度雷諾數然后， RCF可以通過公式（6）進行計算：

其中βH為Hartree壓力梯度因子。

第二，增長因子的發展函數的計算公式是：

第三，可壓縮修正項TCF等于其中壁面溫度可以通過以下公式進行估算：

其中，r是溫度恢復因子，Mae是邊界層邊緣馬赫數、層流邊界層中，r一般等于對于理想氣體，且沒有額外熱源的情況下，邊界層邊緣速度Ue可以通過總焓不變關系式獲得：

其中，γH是比熱比，p是壓強。邊界層邊緣的聲速ae也可以使用類似的方法來計算。此外，ρe可以由等熵關系式ρe=給出。然后，Mae=。對于亞聲速流和跨聲速流，此估計方法對邊界層邊緣速度和馬赫數的估算效果很好。

至此，模式中只有Hartree壓力梯度因子βH尚未求解，該參數與Thwaites壓力梯度因子λθ=有明確的函數關系βH=求解Thwaites壓力梯度因子即可獲得βH。Thwaites壓力梯度因子λθ具體的求解方法見文獻[17，36]。

有效間歇因子的觸發函數表達式為：

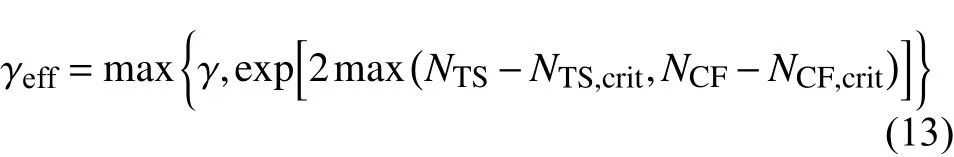
其中，γ是間歇因子，γeff是有效間歇性因子，用于觸發湍流模式中的轉捩現象。轉捩模式與Menter的SST湍流模式之間的耦合方式如下：

注意， γeff是通過控制湍流模式的產生源項Pk,original實現在邊界層內部對層流和湍流的切換。到這里，橫流駐波增長因子的輸運方程已經構造完畢，所有變量均實現了當地化求解。下面將通過兩個經典算例驗證和分析該模式的預測能力。

2 驗證和分析

本文所構建的橫流駐波增長因子輸運模式基于CFL3D程序進行開發，且已經在文獻[35，36]中進行了多次網格收斂性驗證，并且對NLF(2)-0415無限展長后掠翼、鐮刀形后掠翼和橢球大迎角工況等經典算例進行了計算。結果均表明本文所構建的模式在不可壓縮邊界層廣泛的算例驗證中均取得了較好的預測結果。下面將對兩個跨聲速大后掠翼流動進行驗證和分析。

2.1 DLR-F4翼身組合體

DLR-F4翼身組合體在歐洲跨聲速風洞（ETW）中通過溫度敏感涂層（TSP）技術進行了轉捩測量試驗，該構型通常被用于檢驗跨聲速后掠翼表面的T-S波轉捩、激波誘導附面層分離致轉捩和橫流轉捩[39]。機翼前緣后掠角27.1°，試驗數據和穩定性分析結果表明，橫流主導了內側機翼的轉捩，而T-S波失穩或激波誘導附面層分離出現在中部和外側機翼表面。該試驗來流馬赫數為0.785，基于平均氣動弦長的雷諾數為6.0×106，自由來流湍流度小于0.05%，因此可將其視為低擾動環境。宋文萍等[10]在DLR-F4機翼上進行了標準的LST分析，證實了橫流失穩主導機翼內側區域的轉捩現象。此外，與測量所得的轉捩位置相比，文獻[10]指出NTS和NCF的臨界值可以分別設置為10.5和7.5。圖1對比了不同網格尺度下的轉捩預測結果。由圖可知，隨著網格的加密，轉捩預測位置逐漸趨于收斂。最終選擇Fine網格進行所有工況的計算，描述邊界層的O網格內部壁面法向網格單元的數量為401，近壁第一層網格尺度為1×10-6m，與壁面相鄰單元的y+（1）的平均值等于0.95。橫流駐波擾動增長因子輸運模式能夠很好地預測出機翼內側的橫流轉捩。與Coder等發展的NTS模式相結合組成的NTS-NCF模式可以很好地捕捉到橫流不穩定性、T-S波轉捩和激波誘導附面層分離致轉捩。

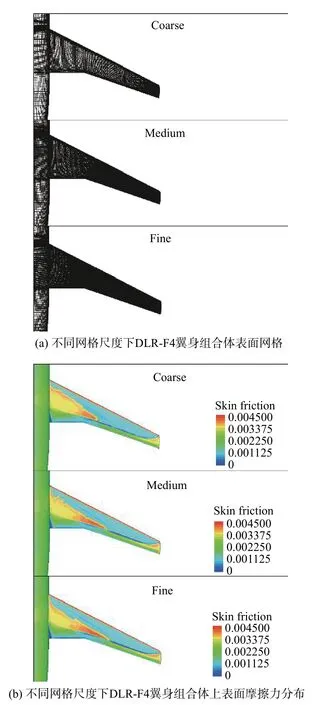
圖1 不同網格尺度下DLR-F4翼身組合體上表面轉捩預測結果Fig.1 Transition prediction results for the upper surface of DLR-F4 wing-body configuration resolved with different grid scales

圖2 DLR-F4翼身組合體上表面轉捩預測結果與風洞試驗結果的對比Fig.2 Comparison of the transition results for the upper surface of DLR-F4 wing-body configuration between the prediction and the experiment

圖2 展示了在迎角α = -0.87°（CL= 0.5）、α = -1.58°（CL=0.4）和α=-2.59°（CL=0.3）時，DLR-F4機翼上表面的摩擦阻力系數云圖與試驗測得的TSP結果。可以清晰地發現，與風洞試驗結果相比，本文發展的

進一步截取α=-0.87°（CL=0.5）工況的上表面的NTS和NCF云圖，如圖3所示。由圖可知，在內翼段（y =0.1 m）處，橫流駐波主導失穩。向翼梢移動，在kink位 置（y =0.24 m）和 接 近 翼 梢 的 位 置（y =0.5 m），則分別是T-S波和激波誘導附面層分離主導失穩。產生這種不同轉捩機制的原因主要是內翼段上表面為順壓梯度，kink處有雙層逆壓梯度，外翼段則為強逆壓梯度，直接導致附面層分離，進而觸發轉捩。這些結論與參考文獻[10]的標準LST分析結果一致。

2.2 ARA翼身組合體

層流模型（LFM）翼身組合體是由英國飛機研究協會（ARA）和西北工業大學（NPU）聯合設計的。它是一架無尾飛機，用于研究跨聲速大后掠機翼（35°）表面的自然層流（NLF）和混合層流控制（HLFC）[40-41]。該翼身組合體于2017年4月在ARA風洞中進行了試驗。風洞中的機身和機翼幾何尺寸如圖4（a）所示；進行CFD數值模擬的Fine網格分布與DLR-F4構型類似，如圖4（b）所示。

來流馬赫數為0.7，參考弦長為0.562 m，參考面積為0.857 7 m2，來流湍流度0.2%，單位米雷諾數為1.2357×107m-1，風 洞 試 驗 迎 角 為-0.99°、-2.16°和-3.34°。傳統的LST分析結果表明NCF,crit值為7.0[40-41]。

圖3 DLR-F4翼身組合體上表面N TS與N CF分布云圖對比Fig.3 Comparison of the contours for N TS and N CF on theupper surface of DLR-F4 wing-body configuration

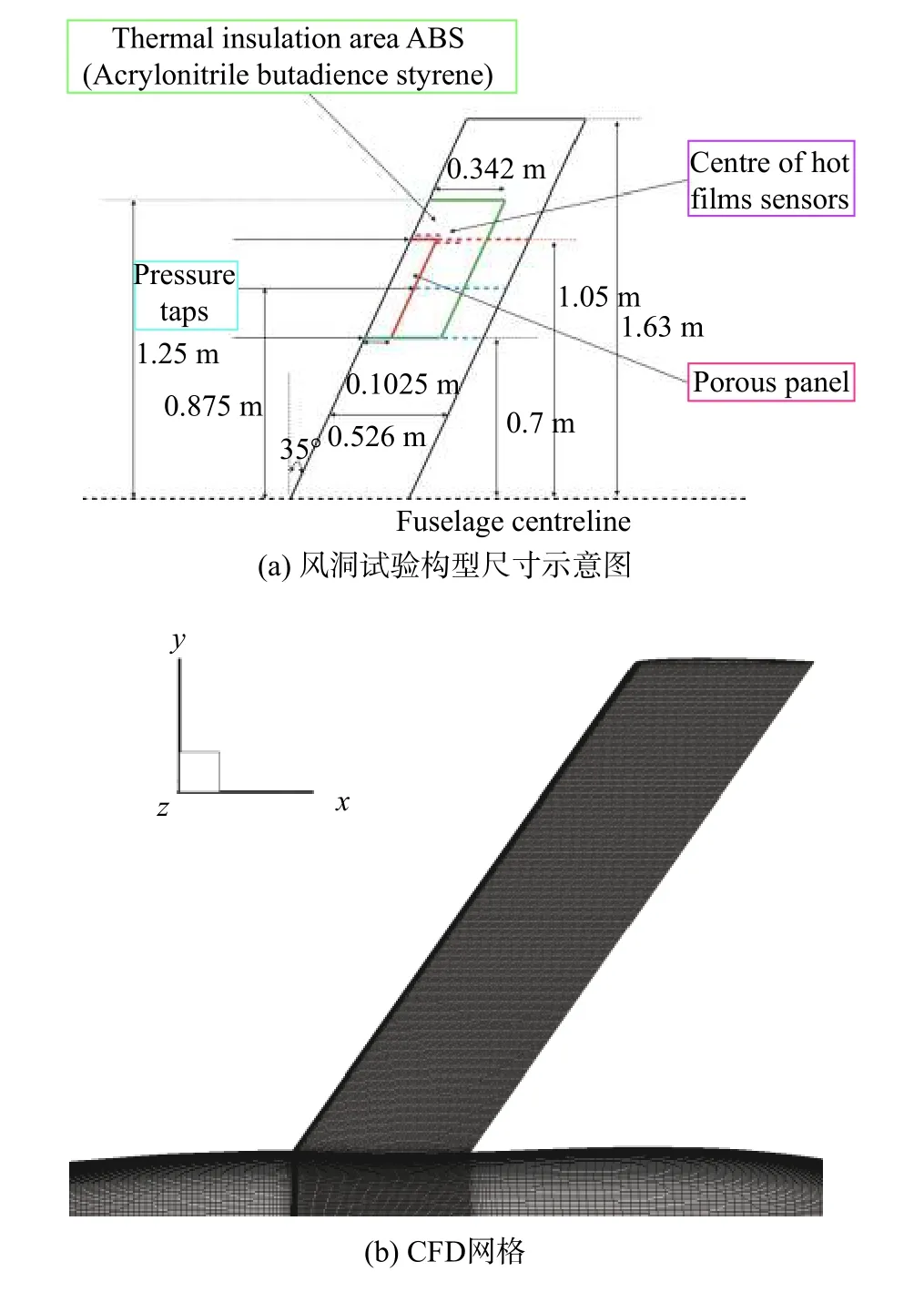
圖4 ARA翼身組合體的風洞試驗構型尺寸和CFD網格圖Fig.4 Wind tunnel model and CFDgrid of ARA wing-body configuration

經過本文NCF模式的計算，在不同迎角下，機翼展向y = 1.05 m位置的壓力分布與試驗結果吻合良好，如圖5所示。圖6對比了本文NCF模式預測所得的橫流駐波NCF因子與傳統標準LST分析結果，驗證了本文模式總是能夠捕捉到最不穩定的最大N值。圖7則展示了在-3.34°迎角下，Coder的NTS模式與本文NCF模式的預測結果對比，可見Coder的NTS模式對于橫流轉捩的預測是失效的，本文NCF模式則能夠較為準確地對橫流轉捩現象進行預測。

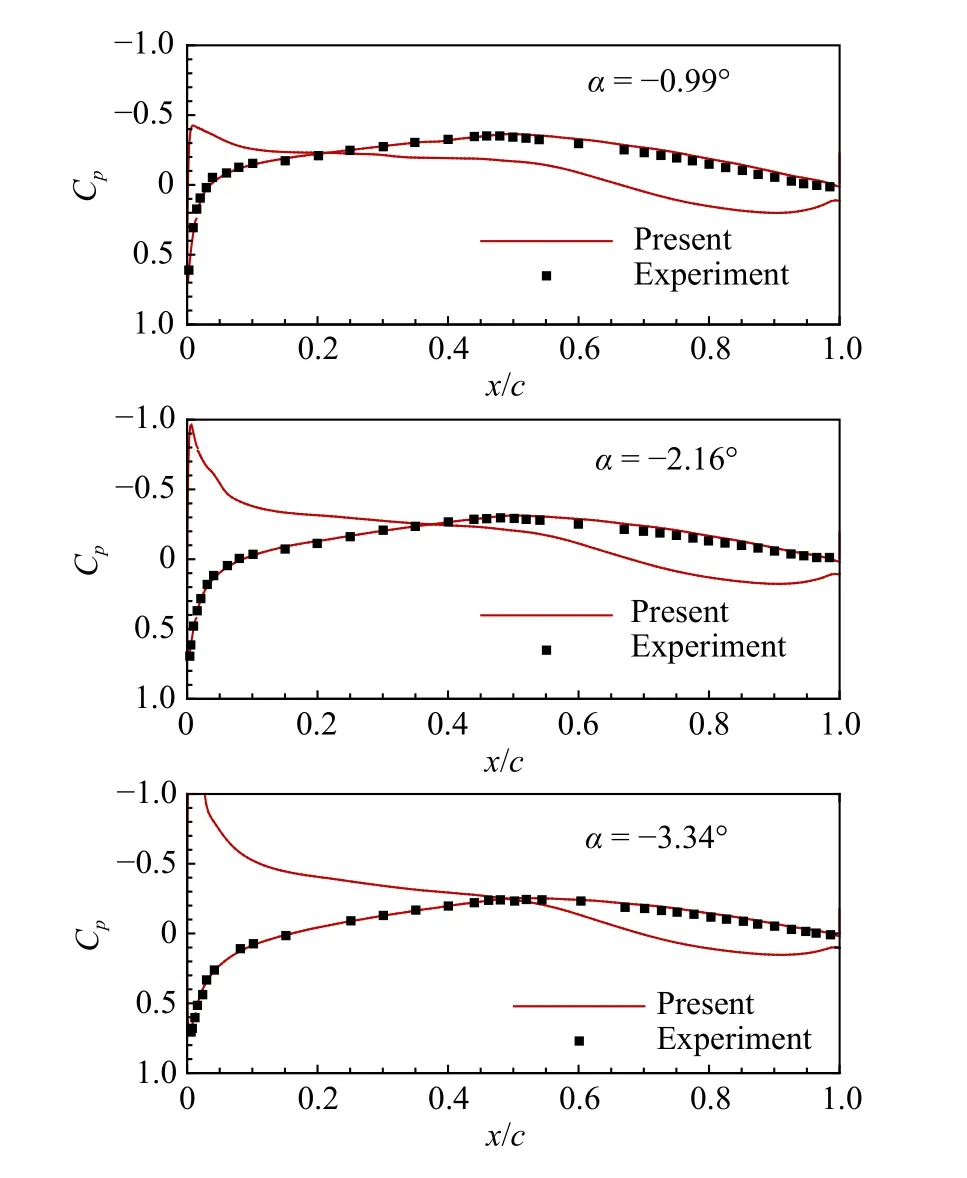
圖5本文模式預測所得不同迎角下機翼表面（y = 1.05 m）壓力系數分布與ARA風洞試驗結果的對比Fig.5 Pressure coefficient distributionson the upper surface of the wing (y = 1.05 m)compared between themodel prediction and the wind tunnel experiment for different anglesof attack

圖8 展示了不同迎角下NCF模式預測結果與風洞試驗結果的對比，兩者吻合良好。風洞試驗顯示機翼上表面出現的鋸齒狀轉捩區也驗證了橫流駐波主導失穩這一事實。由圖5可知，不同迎角下機翼上表面的順壓梯度強弱不同，迎角-3.34°下的順壓梯度最強，因而橫流渦的發展更為迅速，轉捩位置最靠前。DLR-F4機翼前緣后掠角為27.1°，ARA機翼前緣后掠角為35°，鐮刀翼前緣后掠角從0°變化到55°，橢球表面的當地后掠角范圍更大，變化更為劇烈。當地后掠角和順壓梯度這兩個對橫流轉捩非常敏感的影響因素均被本文NCF模式精準捕捉得到，驗證了其合理性和準確性。

圖7 Coder的N TS模式與本文N CF模式預測結果對比（α = -3.34°）Fig.7 Comparison of the prediction results between Coder’s N TS model and the present N CF model (α = -3.34°)

圖8 不同迎角工況下本文N CF模式預測所得機翼上表面摩擦力系數云圖與風洞試驗結果對比Fig.8 Comparison of the skin-friction coefficient contours on the upper surface of the wing between the present N CF model prediction and the wind tunnel experiment for different anglesof attack

3 結論

基于MIT的Drela團隊簡化線性穩定性理論的思想，Coder等基于當地化變量首次構造了流向Tollmien-Schlichting（T-S）波的擾動增長因子輸運模式。本文作者在2019年[35]首次提出了橫流駐波的擾動增長因子輸運模式，并對其進行了可壓縮修正[36]，使其可以適應亞聲速和跨聲速復雜氣動外形的邊界層流動。主要創新點有以下幾個方面：

1）揭示了橫流駐波的最大包絡N值與基本流中邊界層特征厚度、橫流形狀因子、橫流最大速度分量、橫流雷諾數、壁面溫度、邊界層邊緣馬赫數的函數映射關系，并對方程源項的構造進行了可壓縮修正和改進；

2）使用橫流強度因子實現了對橫流最大速度分量的當地化求解，并對計算公式進行了改進；

3）使用螺旋度雷諾數實現了對橫流雷諾數的當地化求解，并對計算公式進行了改進；最終形成了基于當地變量的適用于亞跨聲速邊界層的橫流駐波擾動增長因子輸運模式。

本文選取了純粹針對跨聲速邊界層橫流轉捩的風洞試驗標模。不同迎角導致順壓梯度強度不同，進而使得橫流強度不同，這些都能被當前模式精確捕捉，充分驗證了其在跨聲速工況下的合理性和準確性。未來將繼續致力于讓流動穩定性分析變成一個CFD問題，能夠真正將傳統的穩定性理論推廣到工程復雜外形繞流的轉捩預測。基于線性穩定性理論對超聲速邊界層的Oblique T-S波、橫流波和Mack模態擾動的增長因子進行模式化構造并且探索較為普適的臨界N值判據將是下一步的研究方向。

致謝：感謝史亞云博士和楊體浩博士提供ARA風洞試驗構型和數據。