園區綜合能源系統電／熱／冷多元異質儲能魯棒優化配置

蘇宏偉 崔益偉

（湖北安源安全環保科技有限公司）

0 引言

“碳達峰、碳中和”目標下，綜合能源系統（Integrated Energy Systems，IES）作為提升能源系統整體能效、優化能源結構的重要手段，對于實現雙碳目標、提高能源利用率、促進可再生能源開發有著顯著意義［1］。電／熱／冷等多元儲能作為IES能源子系統融合的紐帶，具有實現多種能源在空間維和時間維上完全解耦的能力。差異化的電-熱-冷負荷及可再生能源（如風電、光伏）的源-荷雙重不確定性使IES中如何合理配置儲能面臨挑戰。

近年來，考慮源-荷不確定性的儲能配置與運行問題受到了廣泛的關注，相關研究主要分為兩類：一類是傳統電力系統中考慮可再生能源出力或電負荷需求不確定性合理配置儲能，該類研究已相對成熟，文獻［2］出了一種考慮二進制變量的能量存儲和輸電線路聯合規劃的魯棒模型；文獻［3］提出了一種微電網優化運行的魯棒優化方法，可再生能源的不確定性輸出變化通過兩個階段互補解決；文獻［4］討論了在可再生能源輸電網絡上集成儲能系統的必要性，并提出了一種儲能魯棒規劃方法。另一類是IES中考慮可再生能源出力或多類型負荷需求的不確定性進行配置儲能［5］。當前，IES領域考慮不確定性影響的研究大都集中在IES的兩階段魯棒優化運行［6］或者隨機優化運行上。雖然有文獻考慮不確定性因素開展IES規劃研究［7-8］，但較少涉及電／熱／冷儲能協同配置。

綜上研究與問題，本文開展了IES中電／熱／冷儲能魯棒優化配置研究。首先，建立確定性電／熱／冷儲能配置模型。其次，在上述模型的基礎上建立電／熱／冷儲能兩階段魯棒配置模型，模型上層為儲能規劃問題，模型下層為IES運行問題。建立不確定性參數集合，該集合用于描述可再生能源供給和電／熱／冷多類型負荷需求的多重不確定性，并且從不確定性參數的數量維度和時間維度兩方面分別引入魯棒測度，解決了傳統魯棒優化過于保守的問題，使得規劃人員能夠根據實際需要更好控制模型的魯棒性。最后利用C＆CG算法分解成主問題和子問題迭代求解。相比于隨機規劃方法或者模糊規劃方法，本文方法不依賴于精確的概率密度函數或模糊函數，僅需不確定性參數的邊界，計算量少并且易于工程應用。

本文其他章節內容為：第2節建立基于EH的電／熱／冷儲能配置通用模型。第3節建立電／熱／冷儲能兩階段魯棒配置模型，并利用C＆CG算法求解。第4節開展算例分析，驗證方法的有效性。第5節為全文結論。

1 儲能配置通用模型

本文基于EH建立綜合能源系統儲能配置通用模型。EH結構如圖1所示。EH將IES的能源形式歸結，到終端需求L和外部供應P，其輸入-輸出耦合關系可以表示為L＝CP。其中L包括電／冷／熱負荷（E-load／C-load／T-load），P包括電網（E-grid）、天然氣網絡（NG-grid）、光伏（PV）以及風機（WT），C包括熱電聯產（CHP）、燃氣鍋爐（GB）、電制冷設備（EC）以及吸收制冷設備（AC），電儲能（EES）、熱儲能（TES）和冷儲能（CES）為待配置設備。

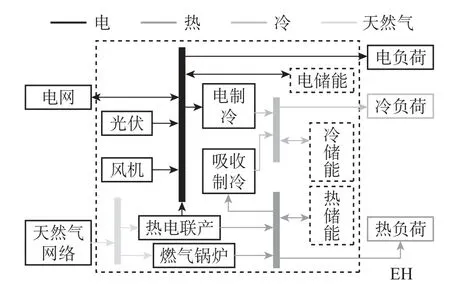
圖1 能源集線器結構

1.1 目標函數

電／熱／冷多元異質儲能投資成本Cinv、IES運行成本Cop、未供負荷成本Ccut的總和最小作為優化目標，目標函數F為式（1）。儲能配置的成本體現在儲能額定功率和額定容量的投資，儲能配置的收益體現在配置儲能后IES運行費用的減少。

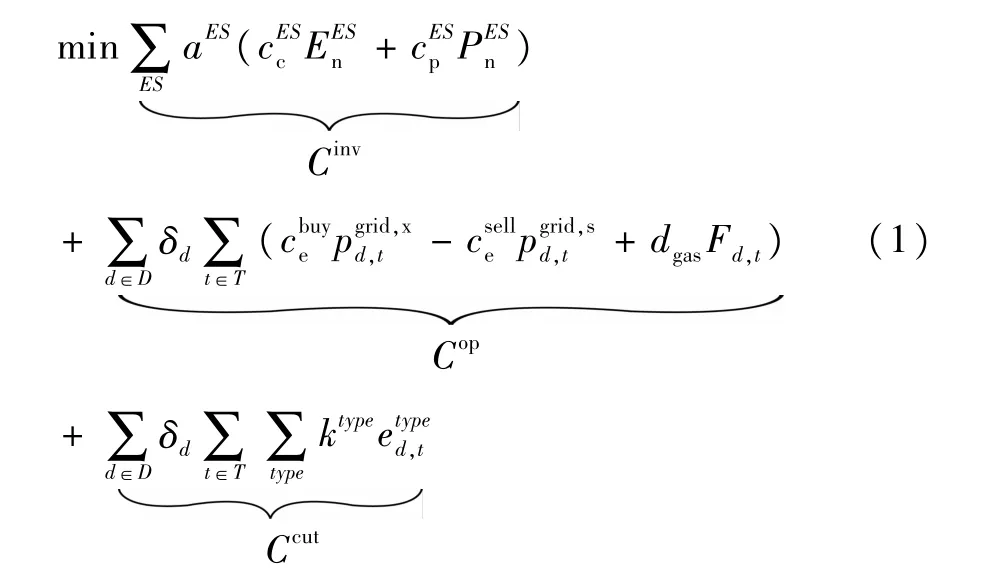
式中，ES為儲能類型，分為電／熱／冷三類，即ES∈｛EES，TES，CES｝；a ES為儲能的等年值系數，由式（2）計算；分別為儲能的單位容量投資成本和單位功率投資成本；為配置的儲能額定容量；為配置的儲能額定功率；D為規劃年的典型日集合；δd為規劃年中第d個典型日發生的天數；T為典型日運行優化考慮的時段數；為IES向上級電網購電的價格；cselle為IES向上級電網售電的價格；為IES與上級電網的交互功率；dgas為天然氣單位熱值價格；Fd，t為IES消耗的燃料；type為用能形式，分為電／熱／冷三類，即type∈｛ele，heat，cold｝；為負荷削減功率。

式中，τ為貼現率；y為儲能壽命周期。

1.2 約束條件

（1）配置約束

式（3）～式（4）表示儲能配置約束，規定允許安裝儲能容量、功率的上限和下限。

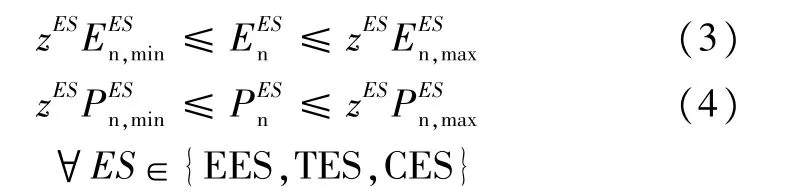
式中，zES為二進制變量，其值為1表示投建類型為ES的儲能，其值為0表示未投建儲能；分別為受安裝場地、并網功率等條件限制，所能安裝儲能容量和功率的上、下限。

（2）運行約束

（a）儲能系統配置和運行約束

建立如下電／熱／冷多元異質儲能統一模型。式（5）表示儲能運行相鄰時段的能量平衡關系；式（6）表示儲能實時容量上下限約束；式（7）表示一個運行周期結束后，儲能所存能量恢復至初始狀態；式（8）～式（12）表示儲能功率約束；式（13）表示儲能對外等效功率。

對于?d∈D，?t∈T，?ES∈｛EES，TES，CES｝：

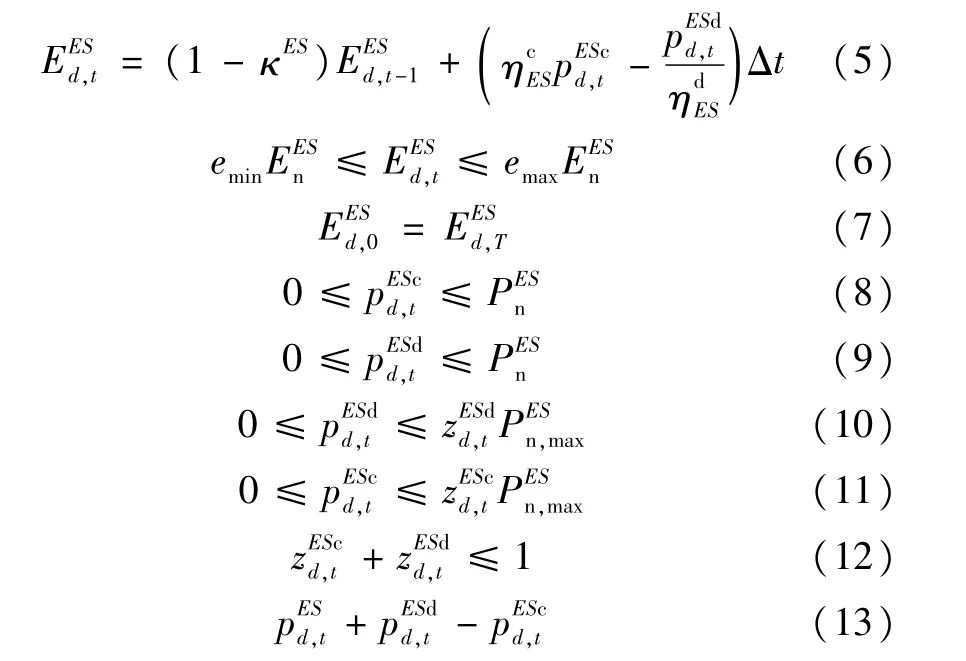
式中，為儲能實時儲存能量；κES為能量自損耗率分別為儲能實時充、放能功率；emin、emax分別為SOC的上下限；均為二進制變量，表示儲能狀態，當儲能充能時，為1，為0；當儲能放能時，為0，為1；為儲能實時功率，規定放能為正，充能為負。

（b）制熱設備運行約束

制熱設備分為熱電聯產和燃氣鍋爐設備。熱電聯產模型為式（14）～式（19），式（14）、式（15）為熱電聯產出力及爬坡約束；式（16）為熱電耦合約束；式（17）、式（18）為熱回收約束；式（19）為棄熱約束。

對于?d∈D，?t∈T：

燃氣鍋爐運行約束為：

（c）制冷設備運行約束

吸收式制冷以熱能為能源，不依賴電力，通過溴化鋰等工質制冷，模型為式（21）。壓縮式制冷消耗電能，通過壓縮機實現制冷循環，模型為式（22）。

對于?d∈D，?t∈T：

（d）切負荷約束

對于?d∈D，?t∈T，?type∈｛ele，heat，cold｝：

（e）功率平衡約束

式（24）表示電母線功率平衡，式（25）表示熱母線功率平衡，式（26）表示冷母線功率平衡，式（27）表示燃料母線功率平衡。

對于?d∈D，?t∈T：

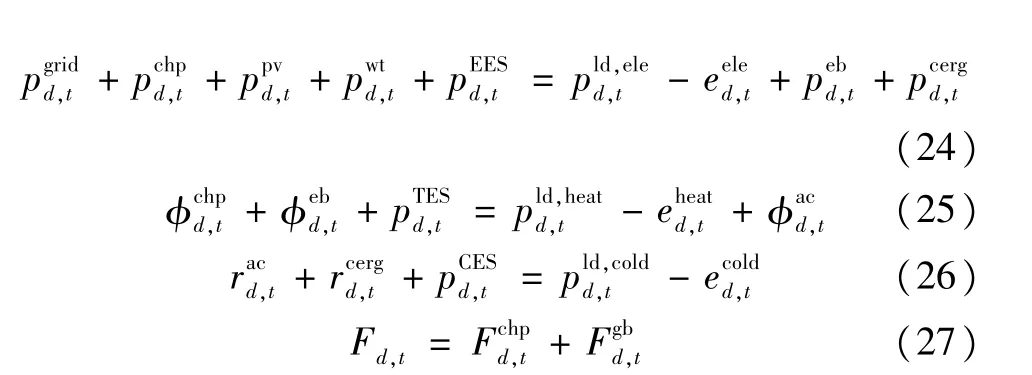
式（24）、式（25）、式（26）、式（27）左邊均為注入母線的功率，等式右邊為從母線流出的功率。在確定性模型中光伏功率和風電功率均為確定性參數，它們來自可再生能源出力預測的期望值。

2 魯棒性模型

（1）不確定性參數描述

不確定性集合的定義是表征不確定因素特性和建立魯棒模型的關鍵。本文考慮可再生電源出力和負荷需求具有隨機性，引入兩個可調的魯棒測度分別描述不確定性參數在數量上和時間上兩個維度的波動。規劃決策者可以根據風險偏好對魯棒測度進行調整，魯棒測度參數越大，則優化結果越保守。不確定性參數集合為U，其本質是一個多面體集合。

對于?t∈T，?i∈｛PV，WT，E-load，C-load，H-load｝：

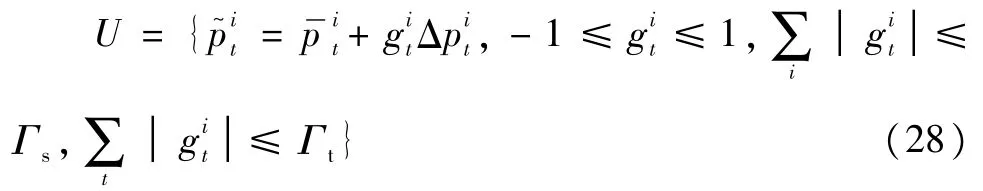
式中，i為隨機單元，包含光伏、風機、電負荷、熱負荷以及冷負荷；為時刻t隨機單元i的功率期望值；為魯棒調整系數；為波動值；Γs為不確定性參數在數量維度上的魯棒測度；Γt為不確定性參數在時間維度上的魯棒測度。

（2）兩階段魯棒優化模型

根據第二節描述的目標函數和約束條件，建立如下兩階段魯棒形式，見圖2。該模型是將儲能配置問題分解成了規劃階段和典型日運行階段。規劃階段主要是求解電／熱／冷異質儲能的額定容量和額定功率，運行階段主要是求解最惡劣情景下的不確定性參數數值和運行優化結果。

（3）C＆CG算法求解

利用C＆CG算法求解兩階段魯棒模型的優化過程為：在規劃階段，根據優化目標給出一組儲能配置結果（主問題），并將該配置結果傳遞給魯棒運行階段；在運行階段，檢驗規劃階段解的可行性，同時根據規劃階段解和優化目標給出一組典型日下最惡劣情景（子問題），并將最惡劣情景傳遞給規劃階段。主問題提供模型下界，子問題提供模型上界，進行循環交互迭代，直到找到滿足條件的儲能配置魯棒解。子問題是雙層max-min問題，可用kkt條件或對偶理論轉化為單層max問題。此外，子問題中一般不能含有二進制變量（如儲能充放電狀態變量等），該類型變量取值通過主問題獲得。

為方便描述C＆CG算法求解過程，本文將圖2所示兩階段魯棒優化模型抽象為如下形式：

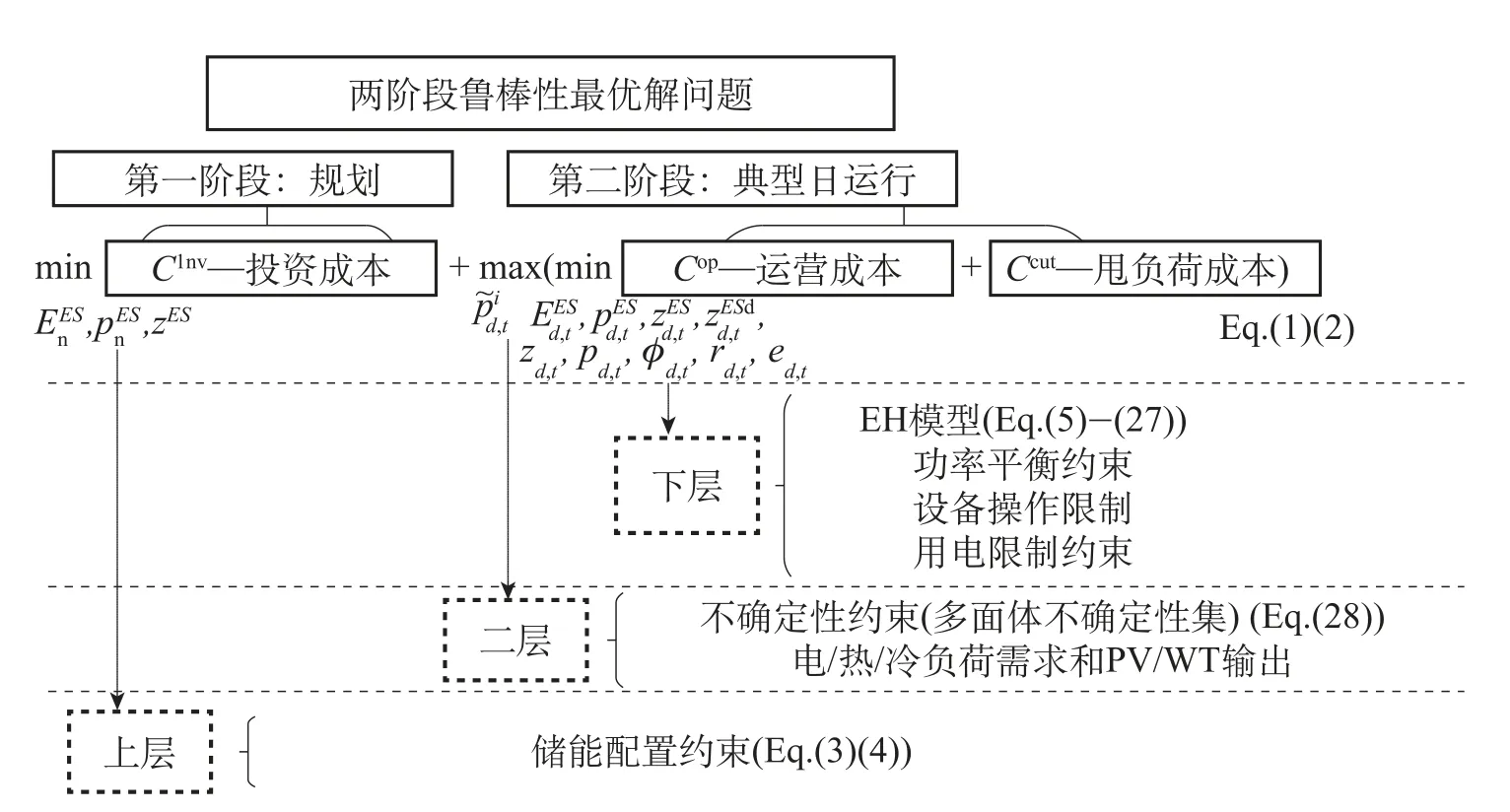
圖2 兩階段魯棒優化模型

式中，y為規劃階段連續變量或整數變量；u為不確定性參數，即風／光出力及電／熱／冷負荷需求；x為運行階段連續變量或整數變量；c，b，A，d，F，G，v，H，I，J，w均為模型約束條件的系數向量或矩陣。約束條件的第一行對應本文模型的式（3）～式（4）。約束條件的第二行對應本文模型的式（5）～式（23）。約束條件的第三行對應本文模型的式（24）～式（27）。U為不確定性參數集合，對應本文模型的式（27）。C＆CG算法求解流程如圖3所示。

圖3 求解流程

C＆CG算法將式（28）分解為上層主問題（MP）和子問題（SP），子問題包含第二層和下層。主問題為式（30），子問題為式（31）：

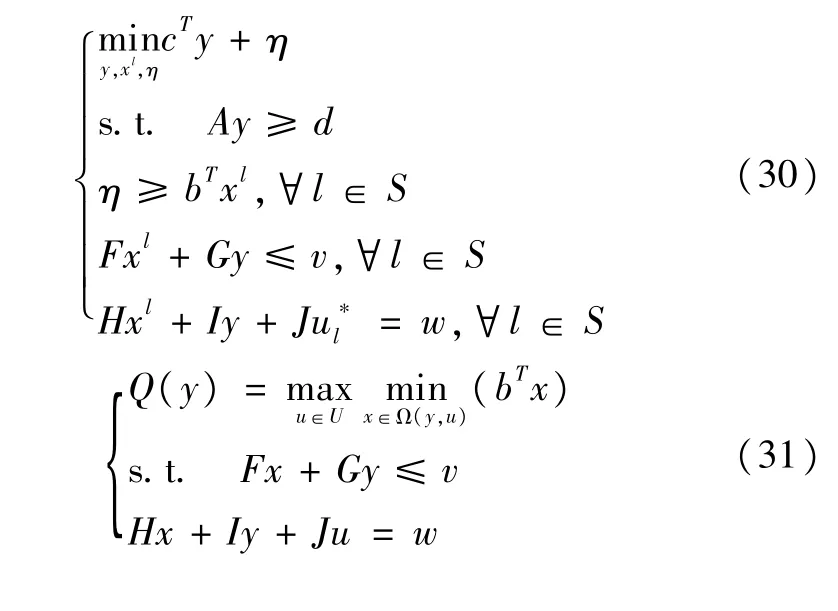
3 案例

（1）算例介紹

本文算例考慮的是一個含電-燃氣輸入，含電-熱-冷3種負荷需求的IES儲能配置問題。IES結構如圖1所示，該IES包含WT／PV、CHP、GB、EC、AC和儲能系統。儲能參數見表1。制熱設備參數：CHP發電效率為0.32，為2.7MW，為1.2MW，均為1.2MW，αchp為1.5。GB的制熱 效 率ηgb為0.81，為0.6MW，為2MW。制冷設備參數：ηac為1.2，ηec為4，為3.2MW，為2MW。取一個典型日表征規劃年，典型日的風光出力及負荷功率期望值如圖4所示，該典型日的δd為365。分時購電電價如圖5所示，售電電價為0.21元／kWh，天然氣單位熱值價格為0.2423元／kWh。

表1 能量存儲參數

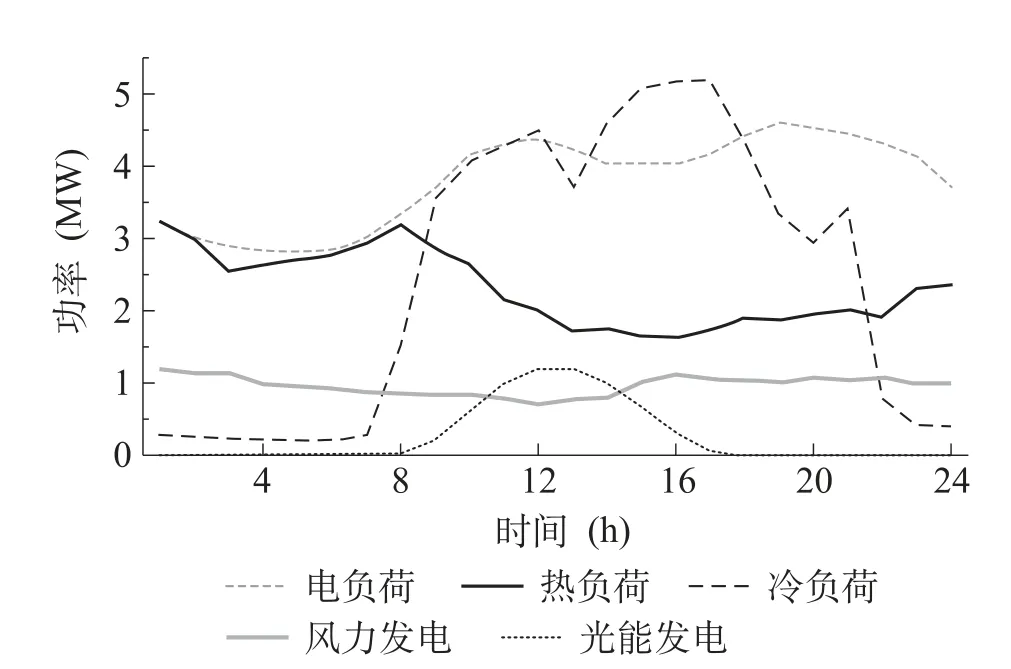
圖4 負荷及可再生能源功率時序變化

圖5 日購電價格變化圖

（2）結果分析

設置兩種規劃模型：確定性模型和魯棒性模型。對于魯棒性模型，不確定性參數波動值取功率期望值的10%，Γs取3，Γt取10。魯棒性模型的CCG算法迭代過程如圖6所示，CCG在第5代成功收斂。兩種規劃方案的結果對比見表2，成本均為年成本即典型日成本的累計。由表2可知，魯棒性模型所配置的電／熱／冷儲能容量均大于確定性模型，這是因為儲能可以抑制不確定性因素的消極影響，因此魯棒性模型配置更多儲能，同時儲能投資成本也更大。

表2 配置方案對比

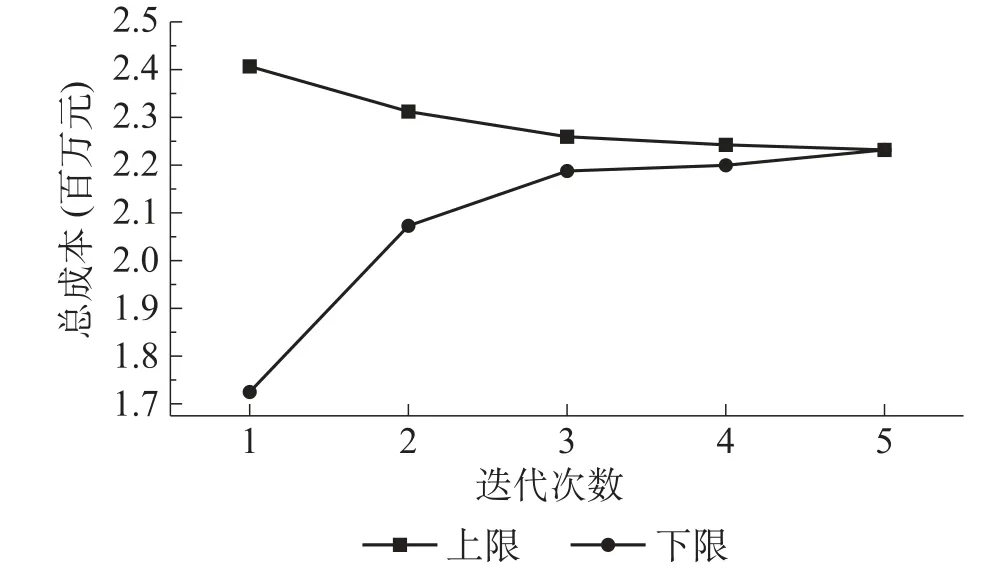
圖6 算法迭代過程

為進一步對比兩種模型，將兩種模型的儲能配置結果應用于單個典型日最惡劣情景（該情景由CCG算法子問題計算得到），IES運行優化的經濟性對比見表3。由表3可知，最惡劣情景下確定性模型購電量更多并且出現了負荷削減，而魯棒性模型購電量更少并且沒有削減負荷，魯棒性模型運行成本相比降低了7.6%，因此魯棒性模型運行經濟性更優。

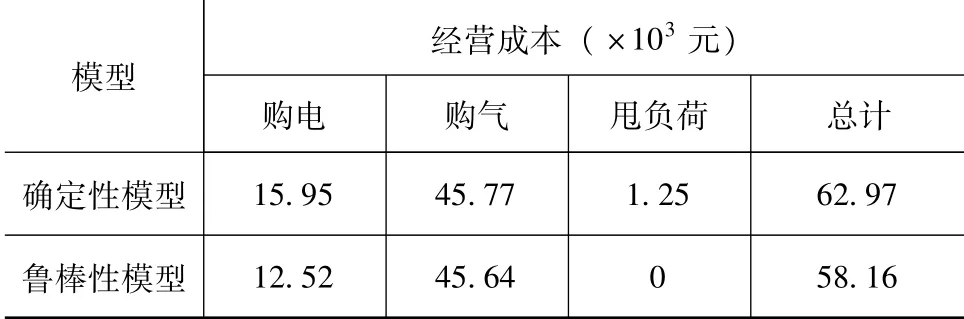
表3 最惡劣情景下的運行成本對比

對魯棒性模型而言，魯棒測度是一個重要參數，通過魯棒測度可以調節模型魯棒性。設置4種魯棒配置方案：M1僅配置EES，M2僅配置TES，M3僅配置CES，M4協同配置EES、TES和CES。當Γt在1～15之間浮動時，4種方案的成本對比結果如圖7所示，儲能容量配置結果如圖8所示。由圖7可知，不確定性越大則總成本越高（即經濟性越差），并且M4的經濟性相對最優，這說明多類型儲能協同配置提高了魯棒性模型的經濟性。由圖8可知，不確定性越大，方案M1、M2、M3配置的儲能容量越多；而M4配置的TES和CES容量先增多后減少，EES容量先減少后增多，這體現了多類型儲能協同配置能夠發揮不同類型儲能間的優勢互補，這也是M4經濟性最優的原因。

圖7 不同魯棒測度下的成本對比

圖8 不同魯棒測度下的儲能配置容量對比

4 結束語

本文提出了一種考慮可再生能源和電／熱／冷負荷不確定性的綜合能源系統儲能魯棒配置方法。基于能源集線器模型，建立確定性能配置模型。在確定性模型的基礎上建立電／熱／冷儲能兩階段魯棒配置模型。為了表征多重不確定性因素，不確定性集合從數量維度和時間維度兩方面分別引入魯棒測度。算例證明了方法的有效性，并表明在惡劣情景下魯棒模型具有更優的經濟性。同時，算例還體現了多類型儲能協同配置發揮了不同類型儲能間的優勢互補。