基于超聲能量擴散的CFST 界面剝離損傷檢測方法與驗證

李 寧，張海月，高樹靈，李忠獻

(1. 天津大學建筑工程學院，天津 300350；2. 濱海土木工程結構與安全教育部重點實驗室(天津大學)，天津 300350；3. 中國地震局地震工程綜合模擬與城鄉抗震韌性重點實驗室(天津大學)，天津 300350)

近年來，由于鋼管混凝土(CFST)結構在強震作用下延性好、剛度大、承載能力高等優點得益于其施工過程快捷高效，正被廣泛應用于各類型工程結構部件中[1]。CFST 結構在施工過程中，核心混凝土的澆筑方式、施工工藝及溫度變化導致的混凝土徐變收縮、CFST 構件受壓初期產生的負圍壓等不利因素，都可能引起核心混凝土與鋼管界面的剝離損傷[2]。一方面，界面剝離損傷削弱了鋼管對核心混凝土的約束作用，導致CFST 極限承載能力、延性及剛度降低[3]，因此鋼管與核心混凝土間的粘結情況一直是一個備受關注的問題；另一方面，由于CFST 構件界面剝離損傷的隱蔽性，傳統意義上的無損檢測手段無法直接檢測到，因而開展界面粘結狀態的檢測具有重要的工程應用需求和實際意義[4]。

針對上述問題和需求，許多學者基于超聲檢測對CFST 剝離損傷檢測開展了試驗及仿真研究。LIANG 等[5]基于超聲阻抗法研究了鋼板與混凝土間的粘結滑移情況，結合均方根差識別滑移發展過程。ZHANG 等[6]利用壓電智能骨料監測低頻循環載荷作用下L 型CFST 柱內部損傷狀況，采用小波包分析損傷指數進行數據分析。許斌等[7]提出基于PZT 的CFST 柱主動界面剝離損傷檢測方法，并采用小波包能量譜的均方根偏差作為評價指標。欒樂樂等[8]建立CFST 界面剝離譜元法模型，探明了應力波在其內部的傳播機理。CHEN等[9]利用隨機聚合方法模擬核心混凝土，數值分析應力波通過CFST 構件不同剝離損傷及微觀骨料時的傳播過程。

以上研究表明，對CFST 界面剝離損傷定量識別迄今為止研究較少，且大部分注重定性地判別CFST 損傷程度，判別損傷范圍十分有限。為了更加全面提取信號損傷信息、定量的對CFST 剝離損傷程度進行描述和檢測，一種對微小損傷敏感、識別準確且能直接表征損傷的方法—超聲能量擴散方法逐漸被廣泛應用[10]。

已有學者基于超聲能量擴散方法，對不同構件中存在的損傷進行定量識別。QUIVIGER 等[11]利用超聲能量擴散有效識別了混凝土中的裂紋，并判別了裂紋數量及深度。IN 等[12]通過擴散超聲波原位監測開裂混凝土在模擬海洋環境下的自愈合過程，表明擴散率可以有效預測自愈趨勢。FARID 等[13]基于超聲能能量擴散法表征鋼筋混凝土板在彎曲試驗中的機械損傷，結論表明該方法能夠區分混凝土構件的損傷階段。AHN 等[14]利用能量擴散系數D及耗散系數σ 表征混凝土試樣的微裂紋，并探討了波頻、壓電換能器的間距對超聲擴散的影響。LU 等[15]研究了結構載荷對超聲能量擴散的影響，得出能量擴散系數與拉伸力指數的關系曲線，在此基礎上可進行螺栓松動預測。WANG 等[16]提取超聲擴散信號損傷信息來識別列車軌道的缺陷，并對鋼軌健康狀態進行連續監測，證明該方法在實際鐵路應用中的有效性。以上研究表明，超聲能量擴散方法中提取的能量擴散系數D及耗散系數 σ 可直接表征損傷，根據兩參數數值可確定損傷尺寸，可提取應力波損傷信息，對損傷分析更全面，因此本文利用超聲能量擴散方法對CFST 剝離損傷進行定量檢測。

本文研究表明，擴散及耗散系數隨界面剝離損傷變化規律明顯，在此基礎上所提出的判定模型可對鋼管與核心混凝土間的界面剝離損傷進行準確、合理的定量評價，為工程實際中的超聲檢測應用提供了重要的理論與方法支撐。

1 超聲能量擴散分析理論

應力波在CFST 中的傳播極其復雜，能量衰減主要包括2 方面：① 由于核心混凝土[17]的內部組成物幾何尺寸的差異，從極微小的未水化水泥顆粒到5 mm～ 40 mm 的粗骨料，顆粒的固有頻率各異，當某種頻率成分通過該介質時，相應自振頻率的顆粒便產生共振，形成新的球面波源使應力波能量不斷減弱；② 鋼管與混凝土組合界面以及粗、細骨料的邊界的反射、折射，使應力波發生不規則的散射、衰減和模態轉換現象[14]。可見，提取應力波在界面剝離處傳播攜帶的損傷信息是分析剝離損傷的有效方法。

應力波在CFST 試件(有剝離損傷)中的傳播過程如圖1 所示，PZT 驅動器在輸入電壓信號的激勵下產生應力波，主要由鋼管外壁處產生的Lamb 波[18]和在核心混凝土內部產生的體波組成，經過帶有剝離損傷的鋼管混凝土后由試件另一側的壓電接收器接收，本文著重于對接收波進行整體能量分析。Lamb 波主要在鋼管薄壁上傳播，體波在鋼管及混凝土中傳播，其中Lamb 波和體波皆存在剝離損傷反射波信息，但是由于Lamb 波為面波能量消散較快且只在鋼板中產生[18]，因此Lamb 中損傷成分較少，在混凝土中傳播的體波所攜帶的損傷信息更多。當存在大面積剝離損傷時，應力波在損傷邊界的反射、折射導致能量衰減及波形的變化，因此本文對接收應力波整體分析其能量特征是識別損傷的有效途徑。WEAVER等[19]基于超聲能量擴散理論，對應力波在混凝土等復合材料中的能量衰減機制進行了分析，結果表明應力波在傳播介質中的能量衰減主要包括2 個方面：① 在傳輸介質中的細小顆粒處產生的能量擴散，其能量損失主要與微顆粒的幾何參數及結構參數有關；② 由于介質振動而產生的能量耗散，主要與基體及介質的材料屬性相關。隨后，WEAVER[21]分析了應力波在泡沫鋁板中的擴散形式，應用能量擴散及耗散系數進行表征，表明上述參數有一定的研究意義。

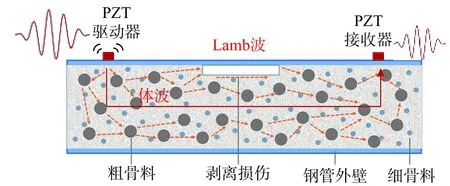
圖1 超聲波在鋼管混凝土中的擴散及傳播Fig. 1 Diffusion and propagation of ultrasonic wave in CFST

假設應力波的擴散與熱傳導過程存在相似的機理，有學者[19?22]利用修正的熱傳導控制方程來描述應力波能量的變化規律，觀測點P 在t時刻的能量變化可用三維超聲能量擴散方程表示：

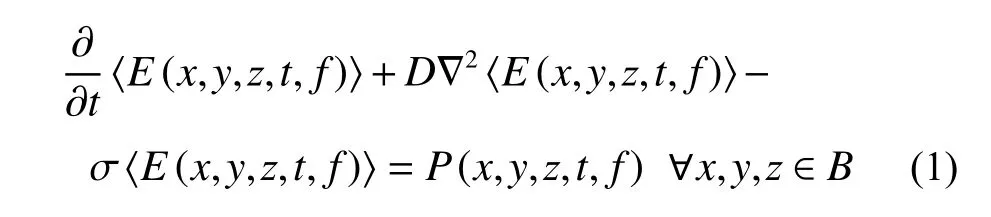
式中：D和σ 分別代表超聲能量擴散系數和耗散系數；P(x,y,z,t,f)代表超聲波激勵信號能量譜密度；E(x,y,z,t,f)代表超聲波能量譜密度函數；x,y,z是三維笛卡爾坐標系的坐標。

式(1)中，D主要受介質內部結構的影響較大，對內部微粒及邊界反射較敏感，包括隨機分布的晶粒及介質中產生的損傷，其值大小與最大能量密切相關。σ 主要與傳播介質的粘彈特性及介質本身的能量吸收相關。損傷的存在改變了應力波的傳播路徑、波能及能量耗散速度，理論上，參數D和σ 皆可有效辨識CFST 剝離損傷尺寸。

式(1)是擴散控制方程，本文對其簡化考慮，三維結構中的超聲能量譜密度可表示為[10]：

式中：E0為初始超聲能量密度；r為信號激勵源與接收器之間的距離。為了求解超聲能量擴散擬合曲線，式(2)可用對數形式表示：

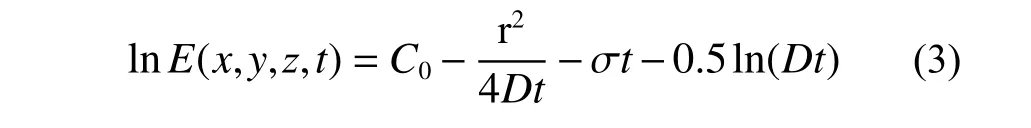
其中，C0代表與信號初始能量有關的常數。根據此方程，通過數值擬合的方法即可求解參數D和σ。

2 鋼管混凝土剝離缺陷檢測試驗

基于《鋼管混凝土結構技術規范》(GB 50936?2014)[23]中對實心鋼管凝土柱的設計規定及試驗設備的限制，本節選取試件尺寸長×寬×高=100 mm×100 mm×300 mm，外鋼管采用Q235 鋼材，核心混凝土采用C30。共設計4 組CFST 試件，每組2 個，各試件4 面皆由不同的損傷工況組成，均布置無損傷面作對比。使用帶凹槽的亞克力板模擬剝離損傷，在澆筑混凝土之前貼于鋼管內壁表面，用有機硅密封膠粘貼好亞克力板四周，防止水分進入。剝離損傷厚度為4 mm。試件各面均貼有對稱的壓電傳感器用來發射與接收信號，具體剝離損傷布置見圖2，損傷工況見表1，剝離損傷尺寸面積占比為0%～28%，涵蓋了工程中出現剝離損傷尺寸面積的大多數情況。其中損傷面積占比Q=SD/STube(剝離損傷面積/相應鋼管面面積)。

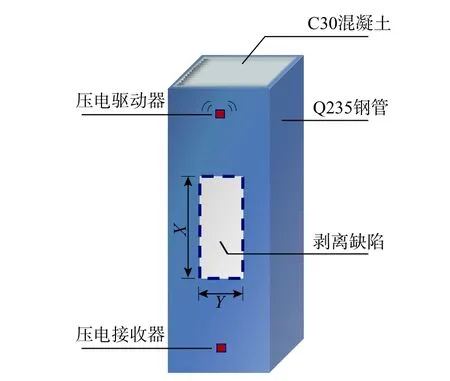
圖2 鋼管混凝土剝離損傷布置圖Fig. 2 Debonding defects layout in CFSTs

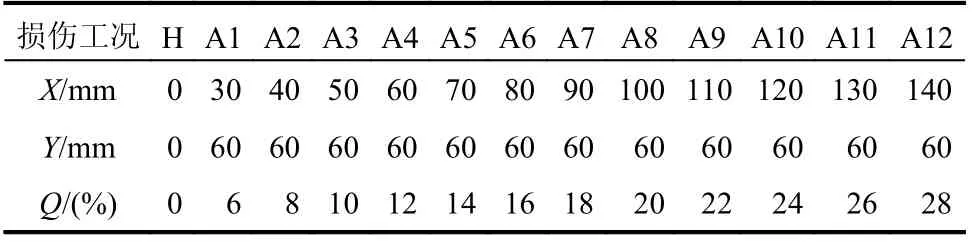
表1 剝離損傷工況尺寸表Table 1 Debonding defects condition size

圖3 為試驗裝置示意圖。圖4 為試驗試件及設備。函數發生器生成峰值為2V 的五峰波(不同頻率)超聲脈沖信號(發射頻率為50 kHz、100 kHz、150 kHz、200 kHz、250 kHz)；寬帶功率放大器將脈沖信號放大20 倍，由粘貼在鋼管外壁的壓電驅動器傳至CFST 內部，由貼在另一側的壓電接收器接收，以25 MHz/s 的采樣率進行采集。

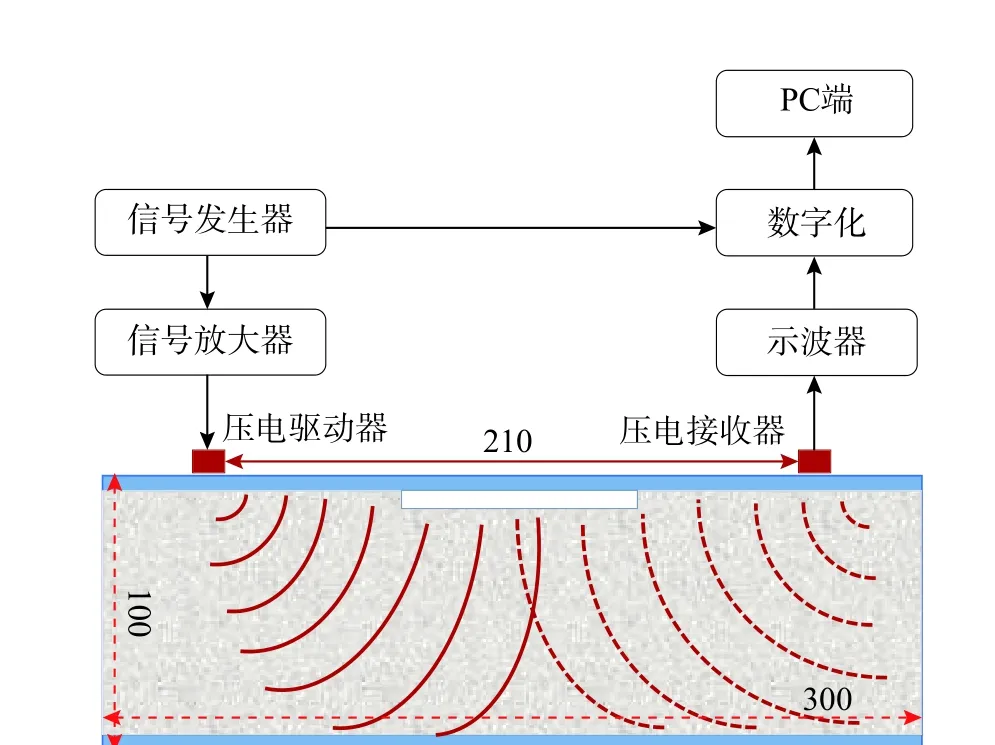
圖3 試驗裝置示意圖 /mm Fig. 3 Test device schematic diagram

圖4 試驗構件及設備Fig. 4 Test specimens and equipment

3 數據處理

為了確定式(3)中C0、D和σ 的值，對信號進行頻域分析。首先，將接收的應力波時域信號(圖5)進行矩形窗劃分，窗長?t取0.14 ms，為了保持信號信息的完整性，窗重疊率取90%。其次，對分窗后的時域信號進行快速傅里葉變換求其頻譜，計算各頻窗的總能量，該能量為其對應的時域信號的擴散能量。最后，對計算得到的擴散能量取對數，按照式(3)對D和σ 進行擬合。

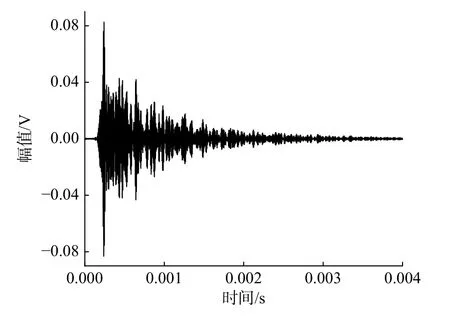
圖5 試件在150 K 激發頻率下的應力波時域圖Fig. 5 Time domain diagram of stress wave of the specimen at 150 K excitation frequency

有學者[11]提出最大能量到達時間ATME對剝離損傷十分敏感，因此本文基于D、σ 及ATME三個參數對CFST 剝離損傷進行研究。數據處理流程如圖6 所示。如圖7 所示，對照時域中的超聲波能量密度數據，以上D和σ 兩個參數可通過式(3)回歸分析來確定，其中的附加參數ATME可通過求解信號能量得到。擬合過程中使用了信賴域算法和加權平方和，最終得到的擴散系數D與耗散系數σ 用于表征本研究中試樣的剝離損傷。

圖6 超聲能量擴散系數數據擬合流程圖Fig. 6 Flow chart of ultrasonic energy diffusion coefficient data fitting operation

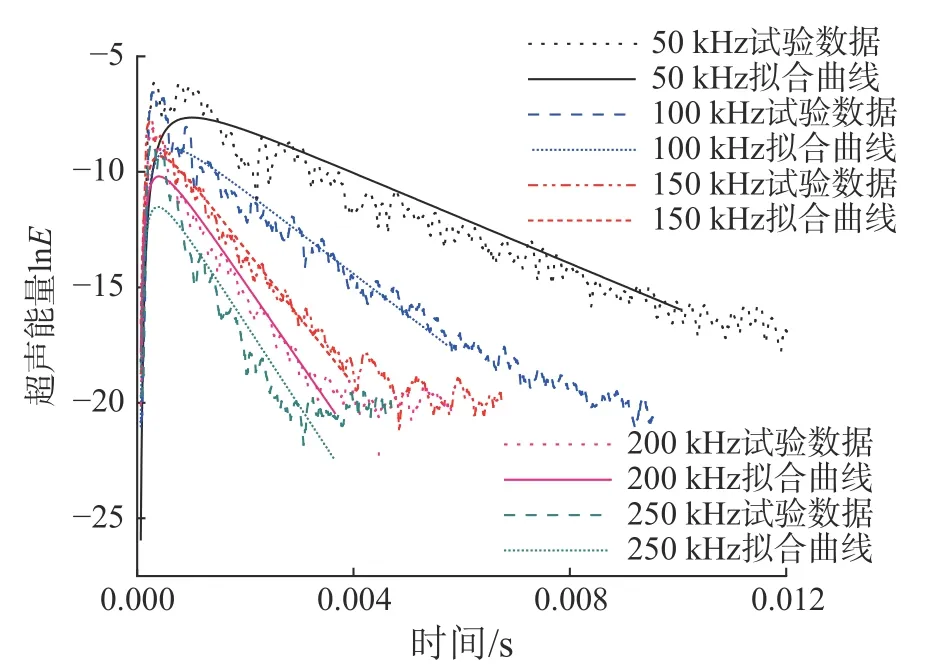
圖7 不同激發頻率下的超聲能量密度曲線Fig. 7 Ultrasonic energy density curves at different excitation frequencies

4 結果與討論

本文選取能量擴散系數D、耗散系數σ 及ATME定量研究上述參數與激發頻率及剝離損傷尺寸的關系。由于混凝土是非均質多相凝聚體且彈性模量相對較小、信號能量衰減較快，因此對混凝土的超聲檢測常用頻率范圍一般在20 kHz ～100 kHz；而外部鋼管是高密度材料且信號能量衰減較小，檢測頻率一般較大。對于兩者組成的CFST 而言，由于CFST 中核心混凝土內部較為復雜[8]，剝離損傷處于混凝土與鋼管兩者界面之間，使用的超聲波頻率較低[17]，本文初選頻率范圍50 kHz ～ 250 kHz。

4.1 超聲能量擴散系數D、耗散系數σ 及ATME與波頻及剝離損傷尺寸的關系

超聲能量擴散主要取決于材料特性以及測試配置(例如激發頻率、環境及溫度)，為了消除本研究可能存在環境條件的影響，整個試驗在無噪聲，溫度、濕度恒定的環境中進行。CFST 剝離損傷和激勵頻率對超聲擴散形為的影響是研究重點。圖7 是無剝離損傷的CFST(Q= 0)在5 種不同激勵頻率下測量的超聲能量密度數據。通過回歸分析得到相應頻率超聲密度數據的最佳擬合曲線。由式(3)分析可知，測量數據達到峰值(圖8 中約為1 ms)的上升部分(即上升至峰值的時間及其幅度)由D決定。相比，圖8 中2.5 ms～8 ms 的實測數據的下降部分(即斜率)由σ 決定[22]。

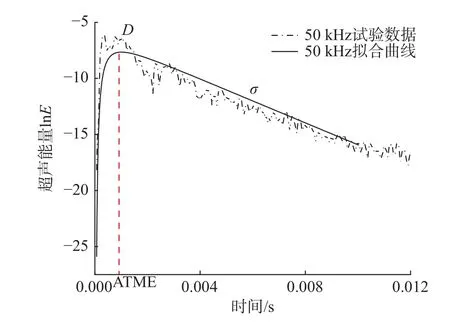
圖8 擴散方程參數擬合示意圖Fig. 8 Fitting plot of diffusion equation parameters

由圖9、圖10、圖11 可知，隨著波頻的增加，應力波能量衰減加快，D減小，σ 增加，ATME減小。由此可知，激勵頻率對超聲擴散影響顯著，因此，激勵頻率是D及σ 的重要影響要素。

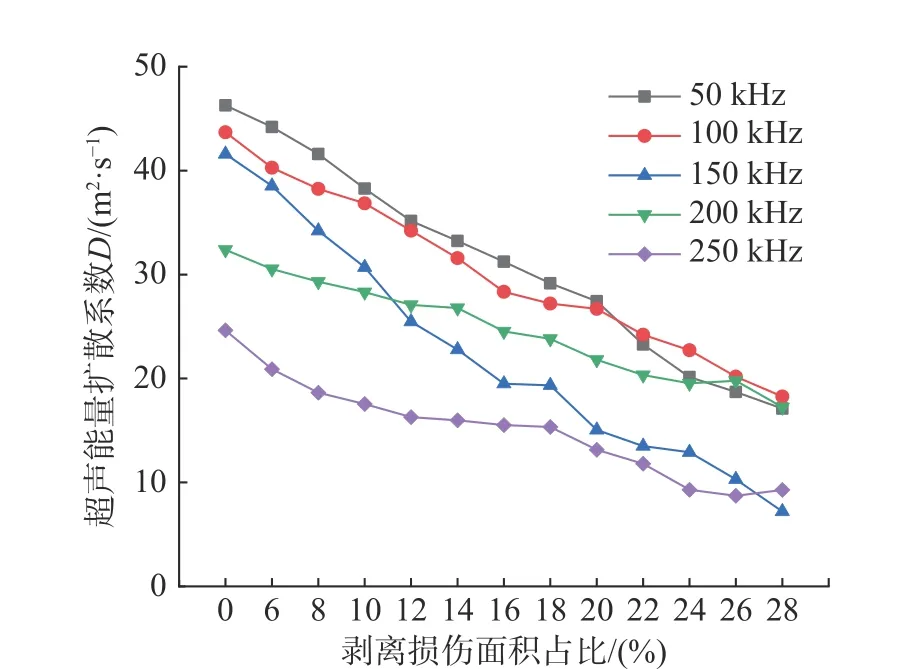
圖9 不同激發頻率超聲能量擴散系數Fig. 9 Ultrasonic energy diffusion coefficient at different excitation frequencies

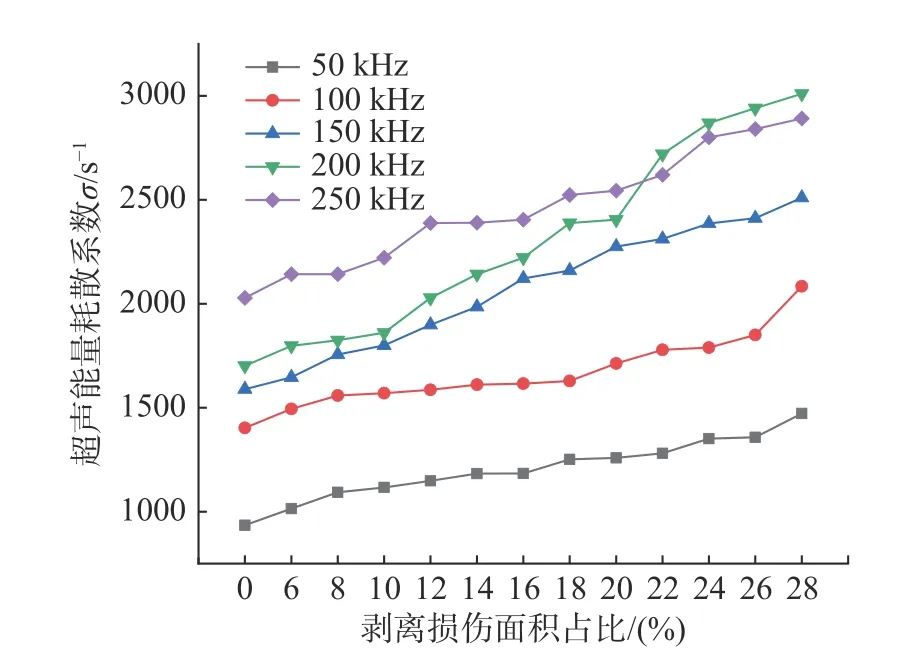
圖10 不同激發頻率超聲能量耗散系數Fig. 10 Ultrasonic energy dissipation coefficient at different excitation frequencies

圖11 不同波頻下最大能量到達時間Fig. 11 Maximum energy arrival time at different wave frequencies

較小的擴散系數意味著從激勵源到接收器的超聲波能量不斷衰減，因此，D值隨剝離損傷尺寸的增加而減小，如圖9 所示。界面剝離損傷的存在增加了應力波的反射、折射及入射波束向周圍的散射，因此到達壓電接收器的應力波能量不斷衰減。可見D值是一個衡量CFST 剝離損傷尺寸的有效參數。

超聲能量耗散系數σ 與傳播介質的材料屬性相關，由圖10 可知，σ 隨著剝離損傷尺寸的增加而增加，整個選定的頻率范圍內，健康工況的耗散值最低，由此可知，當CFST 存在剝離損傷時，信號能量耗散遠大于健康工況。原因是剝離損傷的存在，傳播介質的內部邊界增加，應力波的散射增大，能量耗散增大，并且CFST 剝離損傷的傳播介質主要為空氣，應力波在氣體中傳播相比固體在固體中傳播衰減更快，隨著剝離損傷尺寸的增加，空氣占比更大，因此能量衰減加快，σ 增大。

如圖11 所示，一方面，在不同頻率下ATME呈現下降的趨勢，頻率越高，ATME越小，原因是頻率越高，應力波能量衰減越快；另一方面，隨著損傷尺寸增大，ATME呈現下降的趨勢。原因是，剝離損傷阻礙了應力波向其內部的傳播，更多傳播至鋼管外壁，而波在鋼管的傳播速度遠大于混凝土[3]，因此ATME隨著剝離損傷尺寸的增加而減小。由于ATME不呈現嚴格的遞減趨勢，有一定的數據波動，因此對于CFST 而言，此參數無法充分表征剝離損傷尺寸，故在以下研究中舍棄ATME，研究重點為D及σ。

4.2 最佳激勵頻率的選擇

50 kHz～250 kHz 頻率中，得出適合本試驗的最佳激勵頻率并在此基礎上提出損傷判定模型。將不同波頻及相應的D及σ 進行歸一化，如圖12、圖13 所示。首先歸一化擴散及耗散系數曲線，求解擬合直線斜率，斜率越大，意味著D和σ 隨剝離損傷尺寸波動越大，對損傷尺寸判別靈敏度較高，D和σ 線性擬合后的斜率值如表2 所示。

表2 歸一化D 和σ 線性擬合斜率絕對值Table 2 Unified absolute value of slope of normalized Dand σ with linear fitting

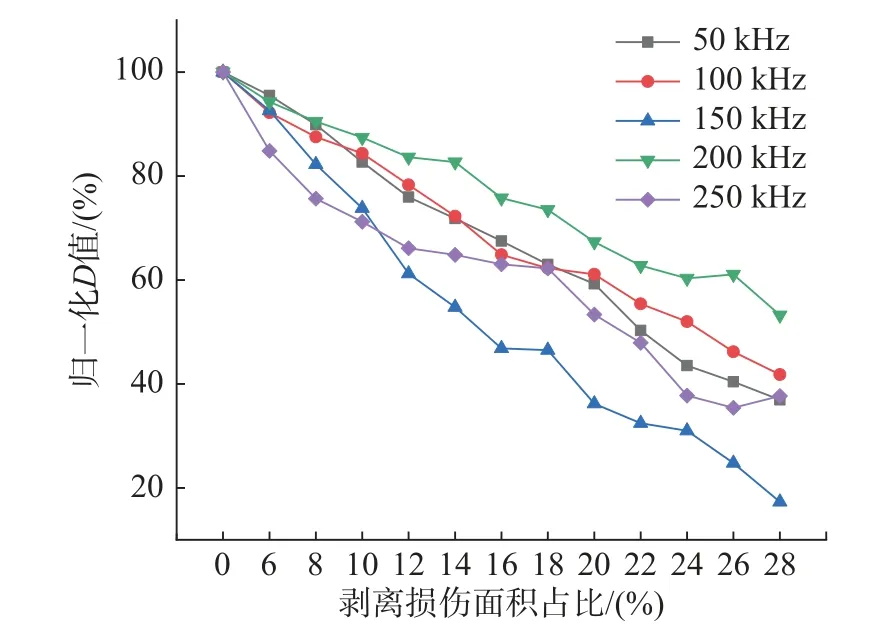
圖12 超聲能量擴散系數歸一化D 值Fig. 12 Normalized Dvalue of ultrasonic energy diffusion coefficient

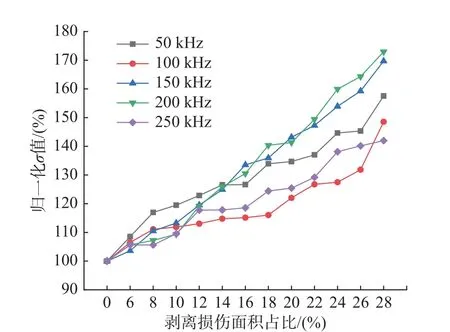
圖13 超聲能量耗散系數歸一化σ 值Fig. 13 Normalized σ value of ultrasonic energy dissipation coefficient

由表2 可知，在激勵頻率150 kHz 下，基于D值的斜率最大且線性擬合系數R2= 97%。對σ，150 kHz 和200 kHz 斜率皆較大，150 kHz 的線性擬合系數R2= 97.28%>95.84%(200 kHz)。因此，150 kHz 為最佳激勵頻率，即此頻率下D和σ 對損傷更為敏感。

5 基于超聲能量擴散定量評估CFST剝離損傷尺寸

基于上述數據分析結論，ATME 對損傷靈敏度較低，其變化不呈現嚴格的遞減趨勢，D和σ 均隨剝離損傷尺寸增加，呈現線性變化的趨勢，因此基于D和σ 提出CFST 剝離損傷判定模型。通過線性擬合最佳激勵頻率150 kHz 下D和σ 與剝離損傷尺寸的判定曲線，提出剝離損傷判定模型。基于判定模型可根據歸一化D和σ 值計算出剝離損傷面積占比Q，判定損傷面積實現定量檢測。判定模型如表3 所示。

表3 D 及σ 剝離損傷判定模型Table 3 Debonding defects criteria of Dand σ

如圖14、圖15 為線性擬合150 kHz 波頻下D和σ 與剝離損傷尺寸的判定曲線，其線性擬合系數分別為97.40%、97.28%，對于在剝離損傷面積占比為0%～28%之間的D值，擬合判定模型與判定曲線最大差值為損傷面積占比6%對應下的8.40%，最小差值為損傷面積占比18%對應下的1.9%，整體平均誤差為3.60%。對于σ 值，除了無損傷工況及損傷面積占比28%工況下，其他工況下兩者值非常相近，在此期間最大差值為3.76%，最小差值為0.03%，整體平均誤差2.53%，均小于5%且線性擬合系數均大于97%，因此，該損傷判定模型是準確的。

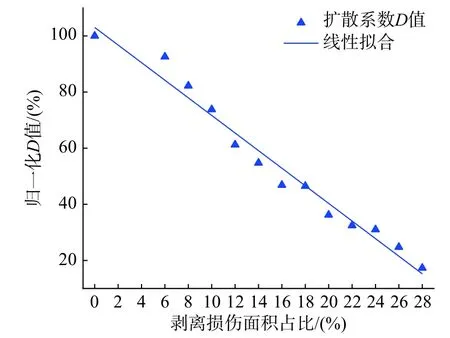
圖14 歸一化D 值線性擬合Fig. 14 Normalized Dvalue with linear fitting

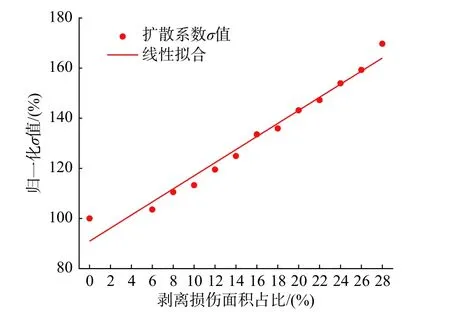
圖15 歸一化σ 值線性擬合Fig. 15 Normalized σ value linear fitting

6 基于COMSOL 的CFST 剝離檢測模型與驗證

本節研究是對上述損傷判定模型的仿真驗證。考慮試驗構件大小、剝離尺寸條件，模擬了不同界面剝離損傷情況下CFST 構件的應力波傳播過程，基于仿真對試驗提出的判定模型進行了仿真驗證。

6.1 基于時域信號的COMSOL 模型驗證

超聲能量擴散法主旨是分析時域信號信息，因此對比試驗及仿真時域信號驗證模型的準確性。圖16 為試驗及仿真時域信號對比。可見仿真信號幅值略大于試驗信號，原因是試驗過程中由于環境、溫度的影響，存在應力波能量損耗，因此幅值略低。兩者幅值均有下降趨勢且波形相似，表明仿真信號較準確。

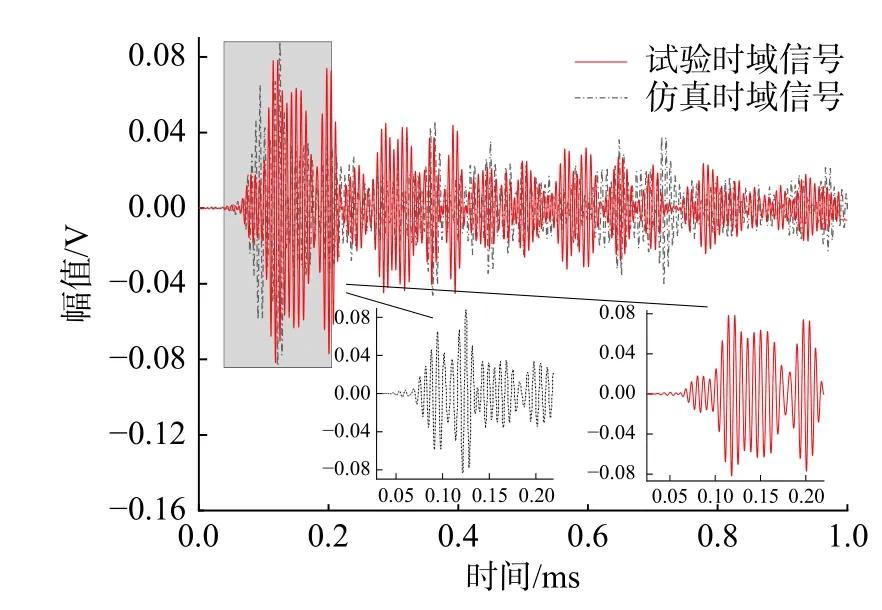
圖16 試驗及仿真信號對比Fig. 16 Comparison of experimental and simulated signals

6.2 基于波速的COMSOL 模型驗證

根據同等條件下的首波波速大小進一步驗證模型的準確性。圖17 為試驗條件下，首波到達的時間Δt1= 5×10?5s，以及兩傳感器之間的距離s=0.21 m，試驗波速V1= 0.21/5 × 10?5= 4200 m/s。圖18 為仿真條件下，首波到達時間Δt2= 5.16 ×10?5s，兩傳感器之間的距離仍為s，模擬波速V2=0.21/5.16 × 10?5= 4069.77 m/s，兩者的誤差百分比為3.1% < 5%，因此基于波速分析的有限元模擬結果與試驗相比是準確的。

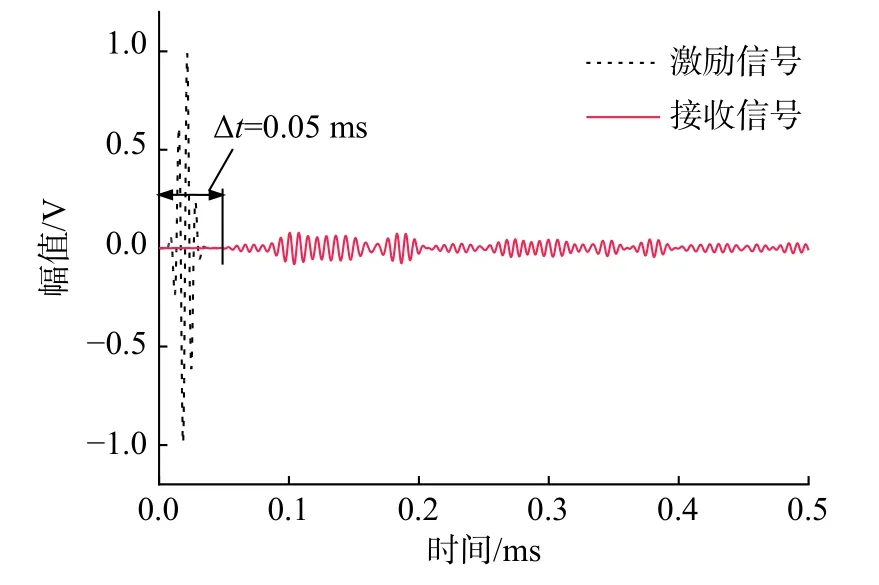
圖17 試驗條件下激勵與接收信號時間差Fig. 17 Time difference between excitation and reception signal during tests

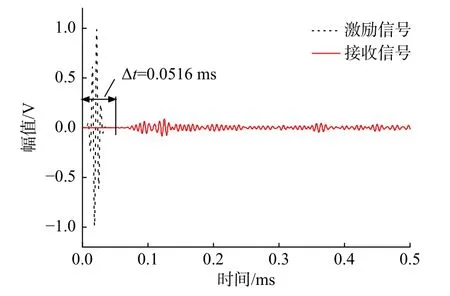
圖18 仿真條件下激勵與接收信號時間差Fig. 18 Time difference between excitation and reception signal in simulation

6.3 基于應力波傳播理論對COMSOL 模型準確性的驗證

本節模擬了CFST 存在界面剝離損傷時的應力波的傳播過程，通過應力波傳播理論對照仿真現象進行模型驗證。為了簡易計算，核心混凝土視為均勻材料。應力波穿過鋼管和核心混凝土之間的界面時，存在反射、衍射及散射現象，且應力波形會發生改變。為了凸顯應力波對界面剝離損傷的敏感性及傳播模式，應用COMSOL 有限元軟件仿真驗證，更直觀觀察應力波傳播過程，以損傷工況為A12(剝離損傷尺寸為60 mm×140 mm×4 mm)的CFST 為例。由于探討界面剝離損傷對應力波傳播過程的影響，因此以鋼管面為主方向觀察應力波傳播過程。

如圖19 所示，首先壓電驅動器激發應力波，主要由Lamb 波和體波組成[18](圖19(a))。Lamb 波主要在鋼管薄壁上傳播；體波向內部核心混凝土傳播，經界面剝離損傷會在鋼管表面發生反射彈射。在3.80 × 10?5s 時刻，應力波不斷發散，經鋼管邊界發生反射并沿鋼管向前傳播(圖19(b)、圖19(c))，此時出現了清晰的波陣面，隨后邊界反射波逐漸耗散，應力波繼續向前傳播，在剝離損傷中心處發生反射現象(圖19(d)、圖19(e))，最后在損傷區域不斷反射，攜帶損傷信息(圖19(f))。

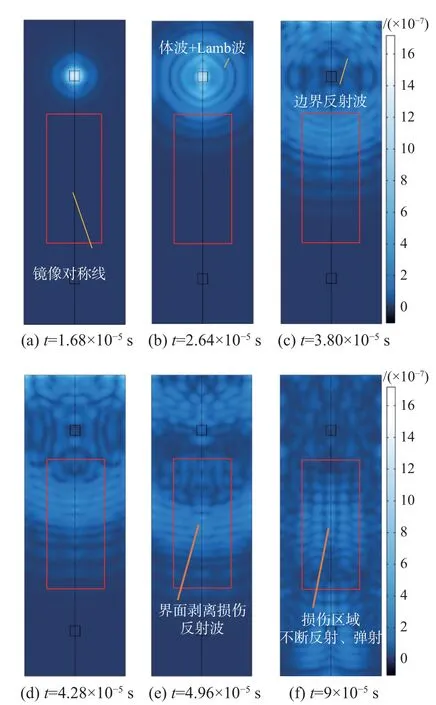
圖19 應力波在帶有剝離損傷的CFST 外壁表面傳播過程Fig. 19 Propagation of stress waves on the surface of CFST with debonding defects

理論上，應力波在傳播過程中不斷反射、折射，能量逐漸耗散且波能伴隨著衰減。界面剝離損傷的存在增加了鋼板邊界條件的復雜性，導致了波不同方向的散射使其波形發生變化。且界面剝離減弱了從鋼管到核心混凝土的傳播，導致應力波在剝離區域反射增加，同樣增加應力波的繞射，這也是存在剝離損傷時傳播時間對比于健康工況下更長的原因。研究表明，在此模型中應力波遇到剝離損傷的傳播過程與理論上保持一致，證明了仿真的準確性。

6.4 基于模擬分析的剝離損傷判定模型驗證

利用COMSOL 有限元軟件對CFST 3 種剝離損傷工況H、A5、A12(Q= 0%、14%和28%)進行數值模擬，目的是得到有限元分析時域信號，求解歸一化D及σ 值對比于判定模型計算求解的歸一化D值與σ 值，驗證判定模型的準確性。

由圖20 可知，歸一化仿真與判定模型D值在不同剝離損傷面積占比時、表現出不一致的誤差，當剝離損傷面積占比分別為0%、14%和28%時，兩者求解的D值誤差分別為3.03%、3.08%和9.33%。其中誤差最大時對應的是剝離損傷占比28%時的工況，其歸一化模擬D值為25.44%，判定模型D值為16.11%，結果表明剝離損傷面積占比越大增加了應力波傳播的不確定性因素，也使得模型仿真與試驗效果差別越大。由于所有誤差項均小于10%，表明本文擬合的擴散系數判定模型是準確的。在此基礎上進一步對比了在不同損傷面積占比下的歸一化仿真σ 值與判定模型σ 值之間的誤差，如圖21 所示。隨剝離損傷面積占比的增加，歸一化仿真σ 值與判定模型求解的σ 值誤差表現出和D值類似的特征。當不存在剝離損傷面積時誤差為9.06%，且隨損傷面積占比的增大誤差項增加，但是仿真及試驗的σ 值呈現相似的變化趨勢，均線性增加，這表明σ 值判定模型同樣準確，能合理地表征CFST 構件剝離損傷的耗散特性。

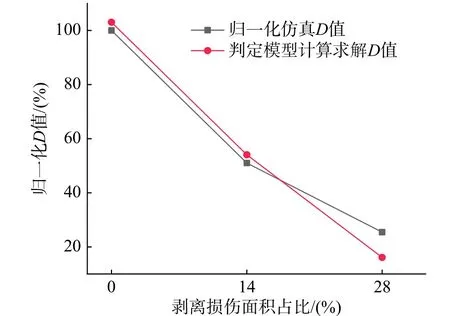
圖20 歸一化仿真D 值與判定模型D 值對比Fig. 20 Comparison of normalized simulation Dvalues and the debonding criteria Dvalues

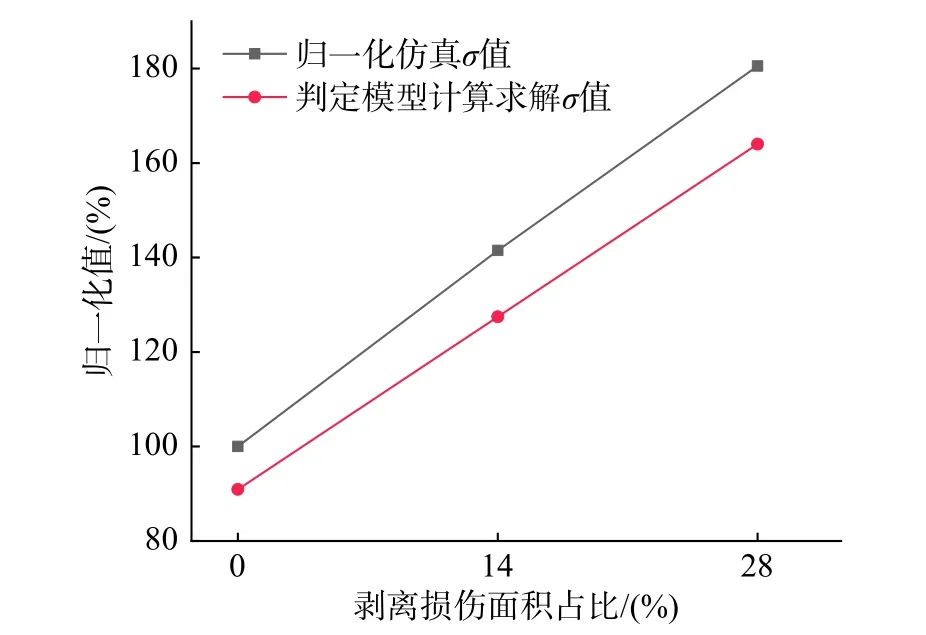
圖21 歸一化仿真σ 值與判定模型σ 值對比Fig. 21 Comparison of normalized simulation σ values and the debonding criteria σ values

7 結論

本文利用超聲能量擴散法擬合超聲擴散及耗散系數，定量表征CFST 剝離損傷特性，研究了在不同波頻下、不同剝離損傷尺寸(剝離面積占比0%～28%)對擴散、耗散系數及ATME 的影響，并且基于歸一化D及σ 與損傷尺寸的關系曲線，提出CFST 剝離損傷判定模型，經有限元仿真最后通過誤差分析驗證了判定模型的準確性。主要結論如下：

(1) 超聲波在CFST 中傳播的波頻選為50 kHz～250 kHz。隨著波頻的增加，擴散系數線性減小，耗散系數線性增大，ATME呈現下降的趨勢。表明頻率是影響能量擴散的一個重要參數，為其他結構超聲檢測頻率選取提供參考。

(2) 對剝離損傷尺寸面積占比為0%～28%，涵蓋了工程中出現剝離損傷尺寸的大多數情況。在最佳激勵頻率150 kHz 下，基于歸一化D及σ 值分別提出剝離損傷判定模型，該模型可對應D及σ 值求解得出CFST 剝離損傷面積占比，實現定量檢測。

(3) 為了驗證判定模型準確性，在試驗相同條件下，利用有限元軟件COMSOL 仿真，對剝離損傷面積不同的模型進行了有限元分析，從時域信號、波速及應力波傳播理論3 方面驗證了仿真模型的準確性。在此基礎上，再通過歸一化仿真D及σ 值與通過判定模型求解得到的D及σ 值對比，驗證了所提出損傷判定模型的準確性。

本文初步采用超聲能量擴散方法對CFST 界面剝離損傷定量檢測，根據擴散及耗散系數提出的剝離損傷判定模型。隨著傳感器工藝、性能提升，后續在實際工程中的應用尚待進一步探索。