Parameter estimation for fractional Vasicek model with discrete observations

Cheng PanhongXu Zhihong

(1.Business School,University of Shanghai for Science and Technology,Shanghai200093,China;2.Institute of Mathematics and Finance,Chuzhou University,Chuzhou 239000,China;3.Public Teaching Department,Rizhao Polytechnic,Rizhao 276826,China)

Abstract：The fractional Vasicek model is a generalization of the classical Vasicek stochastic interest rate model.It can effectively describe the mean reversion and long memory of interest rate series.In order to apply the model to practice,the estimation problem of unknown parameters,i.e.long-term equilibrium interest rate level and the adjustment speed when short-term interest rate deviates from long-term interest rate in the fractional Vasicek model with discrete observations is considered.By applying Borel-Cantelli lemma,Markov inequality and Cauchy Schwarz inequality,the strong consistency of the estimators are proved.

Keywords：fractional Vasicek model,strong consistency,discrete observations

1 Introduction

The Vasicek model driven by fractional Brownian motionwith Hurst parameteris described by the following stochastic differential equation

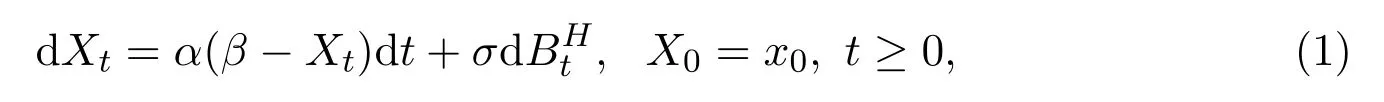
whereα>0,β∈Rare the unknown parameters,andσis a positive constant(see Reference[1]).This model(in short,fVm)has been widely used in many fields,such as finance,economics,hydrology,physics and so on.From the financial perspective,it effectively describes the dynamic changes in the term structure of interest rates.αrepresents the speed of recovery,βis the long-term average interest rate andσis the stochastic volatility.In Reference[2],the fVm was first used to describe the dynamics in volatility.Other applications of fVm can be found in References[3-4]and the References therein.

In model(1)whenβ=0,this model is so-called fractional Ornstein-Uhlenbeck(in short,fOU)process given by

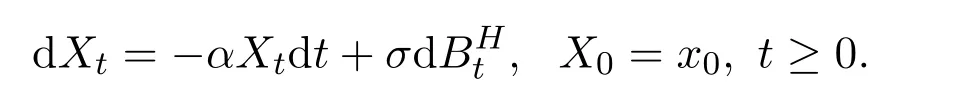
The parameter estimation problem for fOU{Xt,t≥0}has been extensively studied by many authors.In case of continuous observations,Reference[5] first studied the maximum likelihood estimator(in short,MLE)for fOU with continuous observations,and proved its convergence.Reference[6]studied two kinds of estimators about the drift parameter of the ergodic fOU process.The estimators were

and

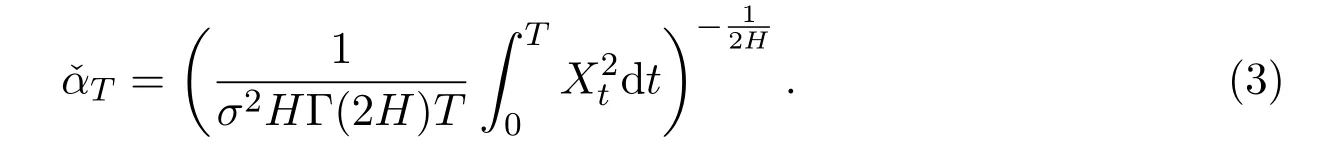
They obtained the strong consistency and the asymptotic property of the estimatorsand.Reference[7]researched the drift parameter estimation by a least squares approach,they got the consistency of the estimator for non-ergodic fOU process and proved that the least squares estimator(in short,LSE)had asymptotic Cauchy distribution.Reference[8]studied the parameter estimation for fOU processes driven by Gaussian processes in the non-ergodic case.More studies about parameter estimation problem for the OU and fOU processes with continuous observations could be seen in References[9-10]and the References therein.

From a practical standpoint,it is more realistic and amusing to consider parameter estimation problem for fOU processes based on discrete observations.Motivated by(3),Reference[11]constructed the estimatorn,defined by

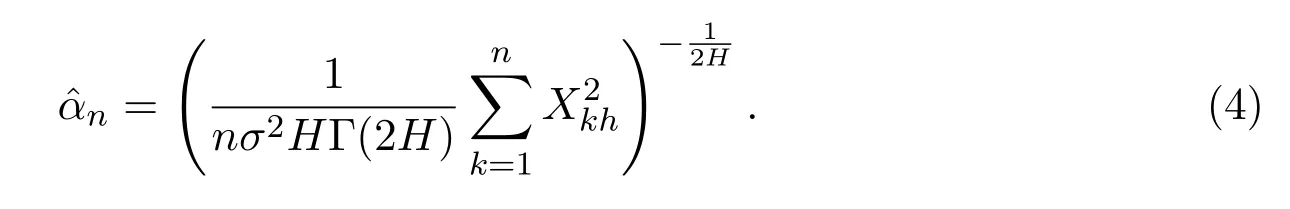
As we know,the fractional Vasicek model is a generalization of fOU process,many authors also analyzed its parameter estimation problem and applications.For example,Reference[16]constructed three kinds of estimators for unknown parameterθ=(α,β)in the fVm of the form,and proved its strong consistency.Reference[17]established the maximum likelihood estimators for unknown parametersαandβin,they proved their consistency and asymptotic normality.Reference[18]considered the two kinds of estimators′asymptotic theory for ergodic and non-ergodic fVm in continuous observations case.Reference[19]discussed the strong consistency and asymptotic fluctuations of unknown drift parametersaandbfor Vasicek-type model driven by Hermite processeswith continuous observations(whenq=1,the model would be the fVm).Furthermore,Reference[20]considered LSEs for Vasicek processes driven by sub-fractional Brownian motions withbased on continuous observations and analyzed the strong consistency as well as the asymptotic distributions of these estimators in both the non-ergodic case and the null recurrent case.

Motivated by the aforementioned works,in this paper,we are interested in estimating the unknown parameterθ=(α,β)in(1)with discrete observations.The reason we do not discuss the estimation forHis that this estimation has been extensively studied.The two simplest and most popular methods are theR/Sanalysis and modifiedR/Smethod.The parameterσis so called volatility,which describes the fluctuation degree ofXt.The reason we also do not study the estimation forσis that there exists many studies(see References[21-22]).The quadratic variation method and maximum likelihood method are generally used to estimate volatility.Due to those reasons,we assumeHandσare known,and just focus on estimatingαandβ.

Assume that the fVm{Xt,t≥0}in(1)is observed equidistantly in time with the step size ?n:ti=i?n,i=0,1,···,n,andT=n?ndenotes the length of the‘observation window’.We also assume that?n→0 andT→∞asn→∞.Our goal is to construct estimatorsnandnbased on the sampling dataXti,i=0,1,···,n,as follows:

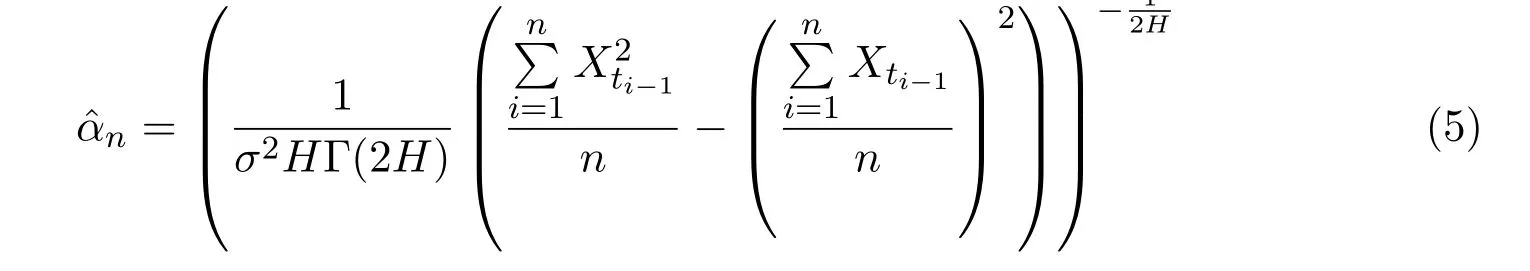
and

We obtain the strong consistency result of the estimator.

The paper is organized as follows.In Section 2,we present some preliminaries for fractional Brownian motion and main Lemmas.In Section 3,the strong consistency of the estimatoris shown.

2 Preliminaries and main lemmas