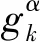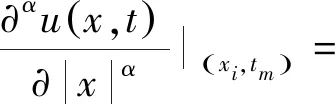一類Riesz空間分數階對流彌散方程的差分方法
張治國,陳豫眉,梁 倩
(西華師范大學a.數學與信息學院 b.公共數學學院,四川 南充 637009)
0 引言
分數階偏微分方程已被廣泛應用于生物、化學和物理等領域[1-6].由于應用背景廣泛并且分數階微分方程難以獲得精確解,故求其數值解尤為重要.目前有不同的數值方法用于求解Riesz空間分數階方程.Meerschaert等[7-8]應用移位的Grünwald-Letnikov公式逼近Riesz分數階導數,提出了無條件穩定的一階差分格式.Celik等[9]使用分數階中心差分公式近似了Riesz分數階導數,提出了無條件穩定的二階隱式差分格式.劉桃花等[10]研究了帶有分數階邊界條件的Riesz分數階對流擴散方程,他們利用分數階中心差分公式離散Riesz分數階導數, 對邊界條件中的左側Riemann-Liouville分數階導數使用標準的Grünwald-Letnikov公式離散.林海欣等[11]研究了帶左側Rieman-Liouville分數階導數邊界條件的對流擴散方程,他們利用分數階中心差分算子離散Riesz分數階導數,同時對于邊界條件則是使用加權和移位的Grünwald-Letnikov公式進行離散.尹修草[12]和曾寶思等[13]研究的分數階對流擴散方程中含有帶整數階的Robin邊界條件,利用中心差分公式離散Riesz分數階導數.古傳運等[14]推廣了含Rieman-Liouville導數的分數階微分方程的比較定理.
給定如下帶有分數階邊界條件的Riesz空間分數階對流彌散方程:
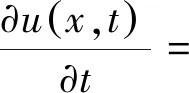
(1)
u(x,0)=q(x),0 (2) (3) (4) 定義中Γ(·)為Gamma函數. 本文主要討論β>0時的情況. 均勻剖分給定區域 (N,M∈Z+)分別為空間及時間步長,則xi=ih(i=0,1,…,N),tm=mΔt(m=0,1,…,M).再令φi=φ(xi), Celik等[9]定義如下分數階中心差分算子: (5) 其中 利用(5)式對(4)式在點(xi,tm)進行近似處理,即: (6) 利用向后Euler差分近似一……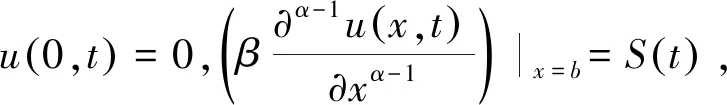
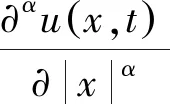
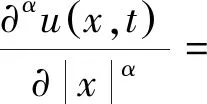
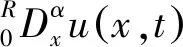
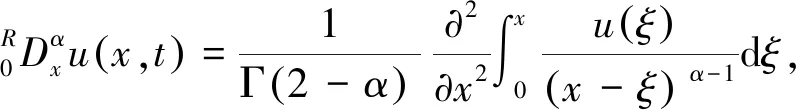
1 差分格式構造及理論分析