用于求解民船裝載問題的R-CS-PSO 混合改進算法

趙小康， 盧厚清

（1.陸軍工程大學， 江蘇 南京 210014； 2. 31151 部隊， 江蘇 南京 210016）

0 引言

裝載問題屬于離散組合優化問題， 有多個不同類型的民船（背包）、多種需要裝載的貨物（物品）和多重約束條件，目標函數不唯一，且解空間是離散點的集合，可以將其歸為多約束背包問題（MKP，Multi-constrained Knapsack Problem）。

MKP 問題是一個NP-Hard 問題， 對于此類問題，國內外很多專家都進行了研究， 目前的解決方法主要分為兩類：一類是精確的求解方法，如枚舉法、動態規劃方法、回溯法和分支定界法等；另一類是用啟發式算法來求解，如貪婪算法、遺傳算法、蟻群優化算法、模擬退火算法、粒子群優化算法等；近年來隨著智能優化算法的不斷發展，布谷鳥搜索算法、雞群優化算法、哈里斯鷹優化算法等新的優化算法也被用于解決背包問題。

采用精確的求解方法雖然原理簡單、容易理解、使用方便，在較小規模的問題上該方法可以得到精確解，取得不錯的計算效果； 但計算時間和計算復雜度會隨著物品數量增加呈指數增長，隨著背包變大和物品數量的增多，用來求解背包問題會浪費大量時間，占用大量存儲空間。使用智能優化算法求解此類問題， 面對不斷復雜化和規模變大的問題， 可以在保持快速收斂計算的同時尋找到一個比較精確的解，在實際應用取得較好的計算效果，對于生產生活具有重要意義。

通過查閱書籍和閱讀文獻可以知道， 使用粒子群優化算法來解決類似0-1 背包類的離散優化問題， 通過向上或向下取整的方式將實數的符號和小數部分去掉，直接轉化為正整數是可行的， 且用該方式求解的速度和解的質量要優于大多數其他智能優化算法[1]，本文我們借助此思想，將布谷鳥搜索算法和粒子群算法結合起來，對算法進行混合改進來求解此問題。

1 粒子群優化算法

粒子群優化（Particle Swarm Optimization，PSO）算法，又稱為微粒群優化算法， 是1995 年美國心理學家Kennedy 和電氣工程師Eberhart 通過觀察鳥群覓食行為，發現其有一定的規律， 進而總結此類行為規律提出的群體智能優化方法[2]。由于算法概念簡明、易于實現，在解決優化問題領域具有優越性， 出現后迅速得到了各國研究者的認可，目前已被用于多個領域。

1.1 算法原理

該算法主要將將鳥群的棲息地鳥巢抽象的看作空間中的解，每只鳥相當于抽象空間中的一個粒子，每個粒子的運動軌跡都是在本身歷史最好位置和所有粒子當前最優位置的影響下，不斷尋找全局最優解的過程[3]。 在該算法模型中，每個粒子都是可行解空間中的一個可行解，都有一個被優化函數目標所決定的適應值， 每個粒子的運動狀態都使用一組速度和位置向量來進行描述。 在初始化粒子種群中，各個粒子在空間中進行不規則的運動，運動過程中，每個粒子都會去尋找本身的最優位置，而整個粒子種群會尋找整個種群的最優位置， 每個粒子的運動都會受到當前自身最優位置和整個種群當前最優位置的影響，經過不斷的迭代后，找到問題的最優解[4]。

1.2 數學模型

該算法的數學模型描述如下：規模為M 的粒子群在一個N 維的搜索空間中以一定的初速度進行不規則運動，xi=（xi1，xi2， …，xim） 表示第i 個粒子的位置；vi=（vi1，xi2，…，vin）表示第i 個粒子的速度；pi=（pi1，pi2，…，pin）表示第i個粒子經過n 次迭代后所經過的最佳位置， 也稱為個體最優（pbest，personal best）；g=（g1，g2，…，gn）表示所有粒子經過n 次迭代后所搜尋到的最佳位置， 也稱為全局最優（gbest，global best）。

在粒子群優化算法中粒子位置和速度的更新公式如下：

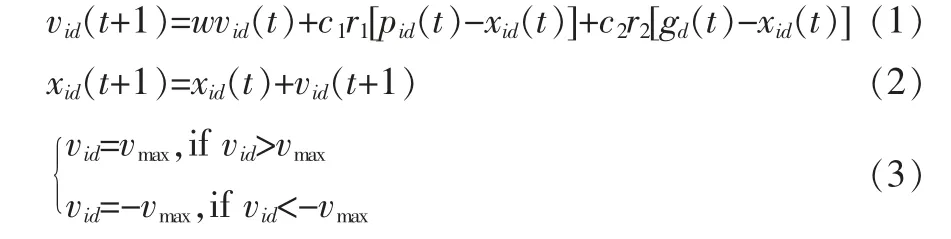
關于該公式中：i∈[1，M]，d∈[1，N]；vid表示粒子的速度，xid表示粒子的位置；w 表示慣性權重因子（inertia weight）；c1、c2為加速常數（acceleration constants），也稱為學習因子；r1、r2為在[0，1] 之間均勻分布的隨機數；pbest表示個體最優解，gbest 表示整個種群的全局最優解。

式（3）中，對粒子的速度vi進行了有關約束，將速度限制在[-vmax，vmax]這一區間；如果vmax過大，粒子就會速度過快，進而飛越最優解；如果vmax太小，粒子就會在很小的范圍內運動，難以進行整體搜索找到全局最優解。

從式（1）可以看出，粒子群優化算法的速度更新公式由三個部分共同構成[5-6]。 第一部分表示粒子的歷史速度對當前速度的影響， 該部分起到了平衡全局和局部搜索的作用， 參數w 是為了平衡粒子的局部搜索能力和擴大對全局的搜索能力而引入的慣性系數。 第二部分反映粒子本身認知模式（cognition modal）影響，表示粒子自身的歷史最優位置對個體速度更新的影響， 使粒子可以在更大范圍內搜索求解，以免只取得局部最優解。第三部分反映社會模式（social modal）對粒子的影響，表示種群中各個粒子受整體中最好位置的影響，并向其靠攏，體現粒子之間進行信息共享、互相學習、互相影響。 在三部分共同作用之下，粒子群基于信息共享，根據歷史經驗，在當前個體最優位置的基礎上不斷變化調整， 以此來尋找整個問題的最優解。

1.3 算法步驟和流程

粒子群優化算法的基本步驟為：

Step1：設置算法有關參數，生成初始種群，生成粒子初始的速度和位置；

Step2：計算各個微粒的適應度函數值；

Step3：計算并更新每個微粒的最好位置，找出每個粒子自身的最優位置pbest 和整個種群的最優位置gbest；

Step4：按照公式（1）更新各個微粒的速度，按照公式（2）更新各個微粒的位置；

Step5： 比較種群中每個微粒當前目標值與其pbest 的目標值， 如果當前目標值更優，則用微粒的當前位置和目標更新其pbest；

Step6： 比較當前所有pbest 和gbest 的 值， 更 新gbest；

Step7： 若未達到終止條件，轉Step4；若達到終止條件， 則輸出gbest 及其目標值并停止算法。根據基本步驟，繪制流程圖見圖1。

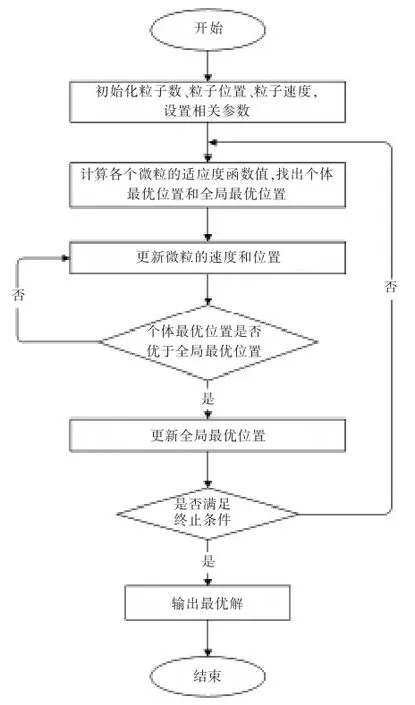
圖1 粒子群優化算法基本流程圖

2 布谷鳥搜索算法

布谷鳥搜索（Cuckoo Search，CS）算法，又稱杜鵑搜索， 于2009 年由劍橋大學Xin-She Yang 教授和S. Deb在研究杜鵑孕育雛鳥行為的基礎上， 結合部分鳥類和昆蟲在飛行過程中具有Lévy 飛行特點提出的一種智能優化優化算法[7]。 該算法提出后，由于其簡單的結構和高效的性能迅速成為研究的熱點，被廣泛應用到諸多領域。

2.1 算法原理

布谷鳥是一種神奇的鳥類，其雌鳥不會自己孵蛋，而是使用侵略性手段占據別的鳥類的巢穴讓其他鳥類幫助其孵蛋，并且鳥巢內一般還會有其他鳥類產下的蛋。有時候布谷鳥會將自己產下的鳥蛋讓其他鳥類一起孵化；有時候布谷鳥為了提高自己產生蛋的孵化概率會將鳥巢內原有的鳥蛋推出巢內；當然，布谷鳥產下的蛋也會被鳥巢主人發現而毀壞或者放棄原有鳥巢重新搭筑巢穴。 在該算法模型中， 布谷鳥產蛋的每個鳥巢相當于解空間的一個可行解，有一個被優化函數目標所決定的適應值，可以用解空間的一個位置來描述，而該位置以符合Lévy 飛行的方式進行變化。

2.2 數學模型

考慮建立算法數學模型的可行性， 布谷鳥的繁殖行為可以理想化概括為以下幾點：

（1） 每只布谷鳥每次隨機選擇一個宿主鳥巢產下一枚蛋，選擇的鳥巢為一個可行解。

（2）在任意選擇的所有鳥巢中，能夠被保留下來，并順利進入下一代的被認為是最好的。

（3）能夠被選擇產蛋的鳥巢的總數量是確定的，鳥巢原主人發現布谷鳥蛋的概率為pα，其中pα∈[0，1]，若被發現，則該鳥巢被淘汰。

（4）布谷鳥按照Lévy 飛行的方式尋找下一個鳥巢并產蛋，代替被淘汰的鳥巢。

布谷鳥搜索算法的具體求解過程如下： 在確定空間里隨機產生一定規模數量的鳥巢并產蛋， 選擇當前最好的鳥巢并存儲，通過步長公式變換鳥巢新位置并產蛋；如果布谷鳥蛋被其他鳥類發現，則代表該鳥巢被淘汰，需更新鳥巢位置，尋找新的鳥巢；尋找最好的鳥巢位置是一個不斷循環迭代的過程， 每次迭代都要計算當前所有剩余鳥巢的位置；不斷重復上面的求解過程，就可以找到鳥巢的最好位置，也就是問題的最優解。

2.3 算法步驟和流程

布谷鳥搜索算法的基本步驟為：

Step1：種群初始化，隨機選擇n 個鳥巢產蛋，生成初始解集；

Step2：計算每個鳥巢的目標函數值，獲得初始全局最優解；

Step3：通過Lévy 飛行更新鳥巢位置，獲得新解；

Step4：由于布谷鳥蛋可能被發現，根據淘汰機制和概率淘汰部分解；

Step5：對現有鳥巢和上一代剩余鳥巢進行對比，將較好的位置保留下來，更新全局最優解；

Step6：判斷迭代條件，若未達到終止條件，轉Step3；

Step7：輸出全局最優解。

根據基本步驟，繪制流程圖見圖2。

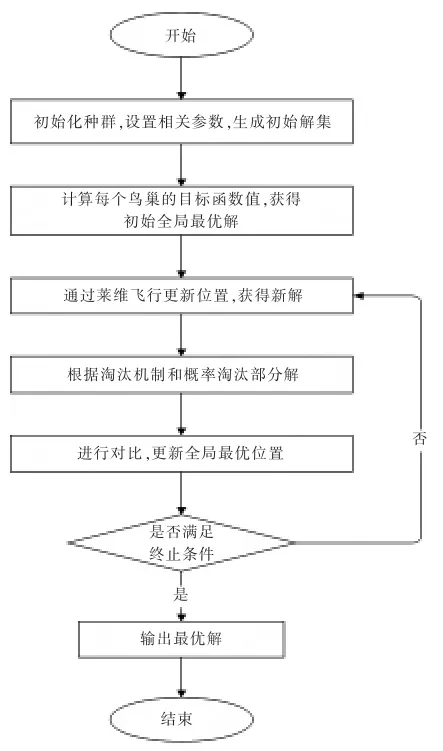
圖2 布谷鳥搜索算法基本流程圖

3 R-CS-PSO 混合算法

每種智能算法都有優點和缺點，沒有一種智能算法能完美的解決所有問題，于是人們在實際使用過程中會考慮對已有的智能算法進行優化改進，在保持算法本身優點的同時根據需要克服不足，以達到更好解決問題的效果。 目前，研究領域對于粒子群算法改進和布谷鳥搜索算法改進都研究的比較多， 也取得了很好的應用效果，解決了很多實際領域的問題，本文在查閱大量文獻基礎上，分析兩種算法的優缺點，將兩種算法混合起來，并引入隨機變化的慣性系數，進一步增進算法的活躍度，以達到取長補短的效果。

3.1 改進思想

粒子群優化算法具有搜索速度快、 尋優效率高的特點， 且粒子可以根據歷史經驗并利用信息共享機制進行位置更新， 但在計算后期大多數粒子容易集中于一個最優解附近，出現早熟和局部最優。布谷鳥搜索算法中鳥巢采用Lévy 飛行隨機游走的方式進行更新，可以在豐富種群多樣性的同時讓搜索范圍擴大， 該算法中使用的鳥巢淘汰機制，也可以使算法跳出局部最優，進而在全局內進行較好的搜索。 R-CS-PSO 算法針對兩種算法的不同特點，將兩種算法的優點結合在一起，有效克服其不足，將布谷鳥搜索算法中鳥巢采用Lévy 飛行進行變化的機制引入粒子群優化算法， 同時也將淘汰機制的理念也引入粒子群優化算法， 不僅有助于粒子在局部范圍進行精細搜索，找到更優的解；而且增加了粒子的活力，讓粒子跳出局部進行更大范圍搜索，進而搜索得到全局最優解。

在算法改進的過程中， 考慮粒子群優化算法中是為了平衡全局和局部搜索能力而引入的慣性系數， 在搜索早期要求有較大速度，也就是較大的，便于在全局內進行快速搜索；在搜索的后期要求速度減緩，也就是較小的，算法可以快速收斂找到更精確的解； 因此提出一種分段隨機的調整策略，使在逐漸縮小的同時又隨機變化，進一步增加粒子的活力，豐富種群的多樣性。

式中：t 表示當前迭代次數；Ndt為設置的最大迭代次數；r0為介于[0，1]之間均勻分布的隨機數；wmax為通過經驗和仿真實驗設置的最大慣性權重系數；wmin為通過經驗和仿真實驗設置的最小慣性權重系數。

3.2 算法步驟

根據改進思想，設計隨機布谷鳥粒子群（R-CS-PSO）混合算法的基本運行步驟如下：

Step1： 程序初始化， 設置R-CS-PSO 算法的相關參數。 主要包括：粒子個數M，最大迭代次數Ndt，學習因子c1、c2，慣性權重wmax和wmin，步長控制因子α，發現概率為pα，搜索上界Ub和搜索下界Lb；

Step7：判斷是否滿足終止條件，若不滿足，轉Step4；

Step8：輸出粒子最優位置和目標函數最優解，終止算法。

3.3 算法流程

根據基本步驟， 繪制流程圖見圖3。

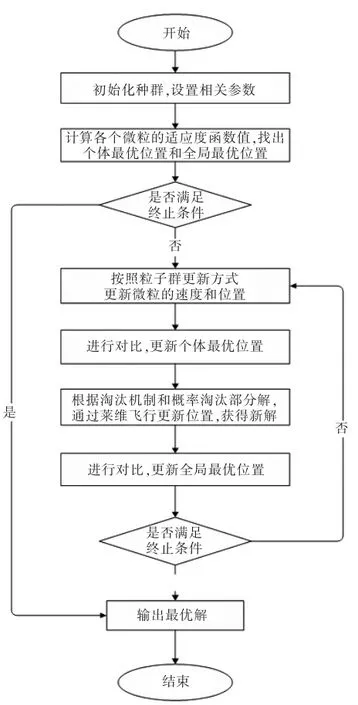
圖3 R-CS-PSO 算法基本流程圖

4 算法性能測試

4.1 使用典型函數測試性能

為了檢驗所提出的RCS-PSO 算法的性能，我們使用Python 語言進行了編程，使用Sphere 函數、Step 函數、Schwefe1_2.22 函 數、Rosenbrock 函 數、Griewank 函 數、Ackley 函 數、Alpine 函 數 和Rastrigin 函數等[8-9]標準的測試函數， 將R-CS-PSO 算法與PSO 算法、CS 算法進行求解速度、收斂性、魯棒性等算法性能比較，通過比較發現，改進的算法相比于之前的算法搜索范圍廣、收斂速度快、能在較短的時間內取得較好的解。

4.2 使用標準背包測試性能

為了進一步檢驗所提出的R-CS-PSO 算法求解背包問題的性能，我們同樣使用Python 語言進行編程，將RCS-PSO 算法與PSO 算法、CS 算法通過經典背包問題進行算法性能測試對比。 選擇以下3 個大、中、小背包[10]，見表1。

表1 2 個經典的測試背包

為了減少隨機性對實驗的影響， 每個測試的結果都是程序獨立運行20 次的平均值，各背包種群規模等于背包大小，最大迭代次數為500 次。 我們分別通過最優值、最差值、平均值、標準差、成功率和迭代次數等指標來分析。其中成功率為每種算法尋優到理論最優值的成功率，迭代次數為每種算法尋優到單次實驗最優值的平均迭代次數。 結果見表2。

分析表2 可以看出， 對于KP-1 背包，R-CS-PSO 算法可以很快找到理論最優解，CS 算法也可以找到理論最優解， 但迭代次數遠大于R-CS-PSO 算法的迭代次數，PSO 算法容易陷入局部最優解；對于KP-2、KP-3，隨著背包的不斷變大，R-CS-PSO 算法可以以一定的成功率找到理論最優解，CS 算法和PSO 算法已不能找到理論最優解，而且從平均值、標準差、迭代次數等也可以看出，RCS-PSO 算法較CS 算法和PSO 算法在解決背包問題中的求解精度、速度和穩定性都更好。

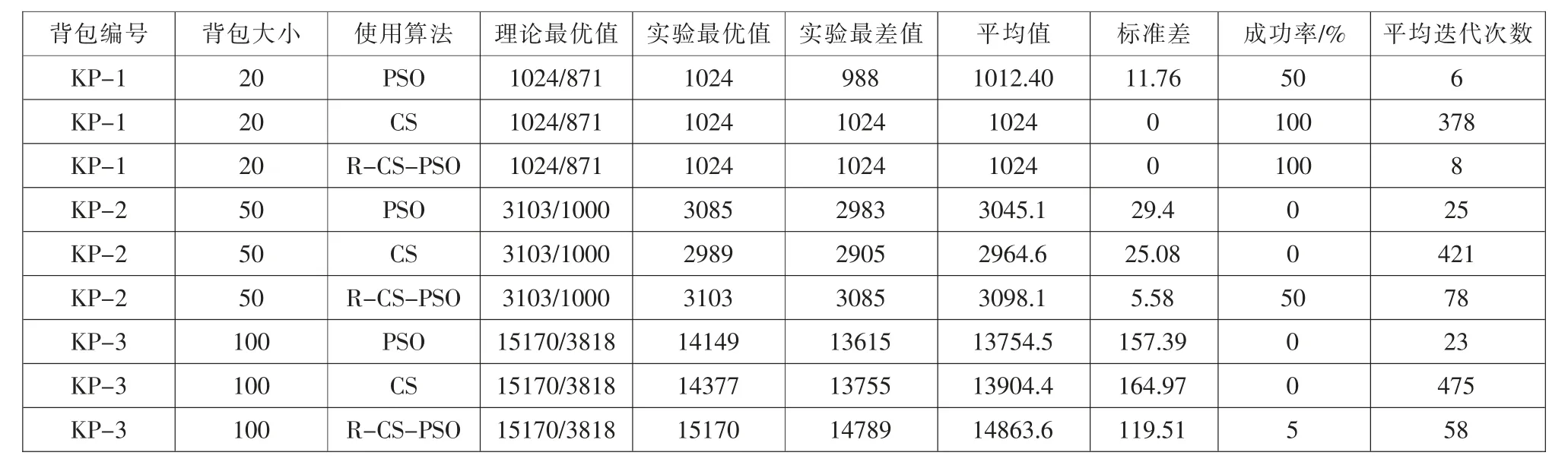
表2 經典測試背包對3 中算法性能測試結果對比

5 結束語

本文在研究粒子群優化（PSO）算法和布谷鳥搜索（CS）算法的基礎上，針對兩種算法的不同特點，改進的提出了分階段隨機布谷鳥粒子群優化算法（R-CS-PSO），通過選擇多個典型函數測試該算法具有較快的計算速度、 較好的收斂性和較強的魯棒性， 通過標準0-1 背包測試該算法在求解多約束背包問題中具有較好性能， 進而在求解民船裝載問題中進行推廣應用。