基于PFC2D的高填黃土減載明洞土體固結蠕變分析

后浩斌，李盛，2*，尤著剛，何永澤

(1.蘭州交通大學土木工程學院，蘭州 730070；2.蘭州交通大學道橋工程災害防治技術國家地方聯合工程實驗室，蘭州 730070)

高填黃土明洞因能較好地適應黃土高原地區山高谷深、溝壑縱橫的地形限制，被廣泛應用于西北地區工程建設中。然而，由于其采用的填料多為黃土，而黃土具有明顯的固結蠕變特性，這將導致土體內部的應力重分布，并對減載材料的減載效果產生影響。同時，若減載材料自身也具有固結蠕變特性，其減載效果的長期有效性也將無法保證。因此，探究黃土固結蠕變對高填減載明洞受力的影響十分必要。

有關固結蠕變的研究多集中于探究其發生的微觀機理及對黃土物理指標變化的敏感性方面。朱才輝等[1]通過對壓實Q3馬蘭黃土進行不同壓實度和不同含水率的蠕變試驗，證明了黃土固結蠕變特性對含水率的敏感度較大，對壓實度次之。葛苗苗等[2-3]和張豫川等[4]分別對壓實黃土進行固結蠕變試驗，驗證了壓實黃土的長期變形特性，分析了黃土固結蠕變對含水率、壓實度、固結應力等單一影響因素變化的響應。周遠強等[5]對黃土固結蠕變的快慢與填土速率、填料壓實度、強夯深度的相關性進行研究，發現黃土的固結蠕變隨填土速率的加快呈線性增加，隨填料壓實度、強夯深度的增加呈線性衰減。Kang等[6]和Wang等[7]分別開展數值模擬和固結蠕變試驗，研究了不同土體在固結蠕變過程中的宏微觀響應。張凱旋[8]從細觀組構演化的角度對黃土的固結蠕變特性及機理進行了深入分析。與此同時，眾多學者在研究高填方結構時也開始關注土體固結蠕變對結構所受土壓力的影響。Mcaffee等[9]采用現場試驗、數值模型等方式研究了管涵填方試驗中，路堤內部土壓力及沉降隨土體固結蠕變的變化規律。文獻[10-12]通過現場試驗研究了高填黃土減載明洞土壓力及結構內力的分布規律，并推導了高填明洞土壓力計算公式；姚玉相等[13]利用數值模擬確定了明洞采用聚苯乙烯泡沫板(expanded polystyrene boar，EPS)板減載時的最優參數取值。趙亮亮等[14]分析了槽寬比、邊坡坡角等的改變對高填減載明洞土壓力變化的影響。

然而，針對黃土固結蠕變特性對高填減載明洞長期土壓力分布及對減載措施實際效果的影響鮮有報道。為此，以離散元軟件PFC2D建立虛土減載的高填黃土明洞數值模型，探究了黃土固結蠕變對虛土實際減載效果的影響；分析了不同填方深度處土壓力及豎向位移隨黃土固結蠕變的發展規律；并通過土顆粒間接觸力鏈的演化規律，從細觀層面對黃土固結蠕變過程中土顆粒間的接觸變化及虛土減載的荷載傳遞機理進行分析；最后，通過參數化分析進一步探究了土體固結蠕變條件下，虛土厚度、寬度和矢跨比的改變對明洞受力的影響，得到虛土減載時的最佳參數，以期為高填黃土減載明洞在設計、施工中考慮土體固結蠕變的影響以及采取合理的設計參數以優化明洞設計提供參考。

1 基于離散元法的數值模擬

1.1 模型的建立

所建立的高填黃土減載明洞模型如圖1所示。模型總高H=41 m，底寬B=13.8 m。明洞高h=11 m，跨徑b=12.8 m，邊坡坡腳70°，虛土位于明洞頂，厚度T=5 m，寬度W=12.8 m，沿明洞中軸線對稱設置；明洞頂以上覆土高度H1=30 m。模型邊坡、明洞、地基均采用wall單元模擬，填土和虛土為黃土，用ball單元模擬，填土壓實度設置為96%，虛土壓實度為85%。為了使數值模擬的結果符合實際情況，在建立模型時，采用改進的分層壓實法(improved multi-layer compaction method，IMCM)[15]將填土分7層填筑，以避免生成初始模型時產生過大的水平應力。為保證頂面土體被壓實，留白區2 m。

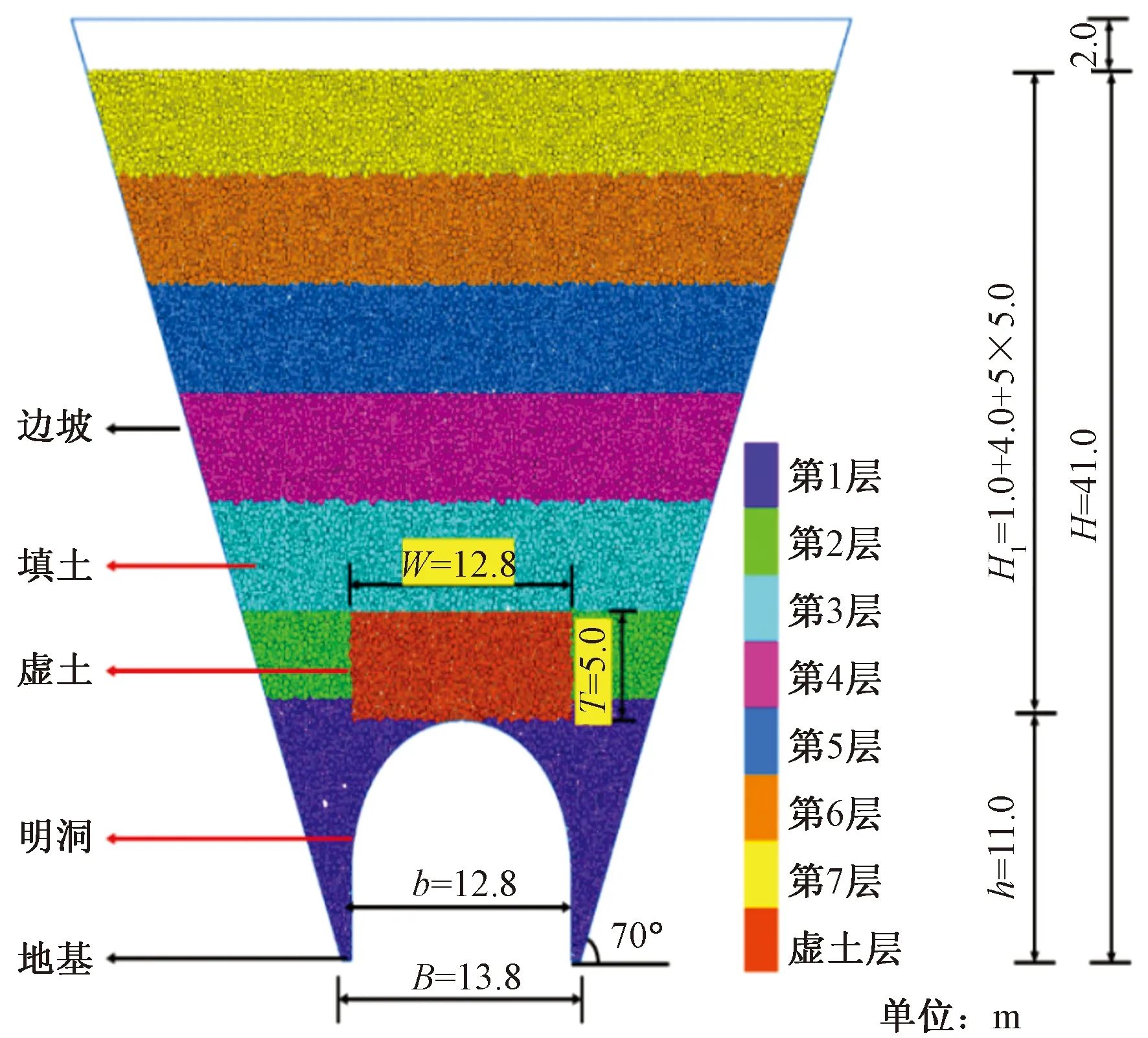
圖1 層次模型

為了監測伴隨土體固結蠕變，明洞洞頂、明洞不同填方深度處的豎向土壓力和豎向位移以及填土表面沉降的變化情況，分別在A-A、B-B、C-C、D-D截面布置了一定數量的編號測量圓。其中，A-A截面處1～9號測量圓監測明洞頂豎向土壓力隨土體固結蠕變的變化及洞頂平均豎向土壓力大小；C-C截面處5、10、11號測量圓及D-D截面處12、13、14號測量圓分別監測不同填方深度處的土壓力及豎向位移隨土體固結蠕變的變化；B-B截面處水平布置的一排測量圓監測填土表面沉降隨固結蠕變的變化。測量圓具體布置如圖2所示。

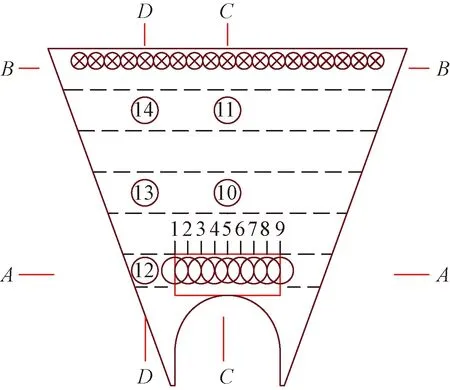
紅色矩形區域為設置虛土區域

1.2 本構模型的選擇

選用PFC2D內置的Burgers本構模型來描述荷載作用下填土和虛土的固結蠕變行為，其本構方程為

(1)

式(1)中：EM為Maxwell體彈性模量，MPa；ηM為Maxwell體黏性系數，MPa·h；EK為Kelvin體彈性模量，MPa；ηK為Kelvin體黏性系數，MPa·h；EM、ηM、EK、ηK均為本構方程中表征填土和虛土固結蠕變行為的宏觀參數；t為固結蠕變的時間，h；σ0為初始應力，kPa；ε(t)為初始應力σ0在t時間內產生的應變。

1.3 材料參數的獲取

使用的相關概念說明如下：①“土體”指代“填土及虛土”；②以第7層填土填方完成時刻(S0階段)作為土體固結蠕變前后的分界;③填方完成時刻以前為固結蠕變前階段，未考慮土體固結蠕變；④填方完成時刻之后為固結蠕變階段。

與有限元軟件能夠直接識別控制材料力學特性的宏觀參數不同，PFC2D程序是通過識別與宏觀參數對應的細觀參數進行模擬分析的。因此，研究過程中需依次獲取三項材料參數：①土體固結蠕變前的細觀參數；②填方完成時刻之后，土體固結蠕變時Burgers本構模型中的宏觀參數；③與Burgers模型中的宏觀參數相對應的表征土體固結蠕變的細觀參數。具體過程為：土體固結蠕變前的細觀參數通過建立數值雙軸壓縮試驗模型，利用參數標定的方法獲取的。即通過不斷調整控制顆粒整體宏觀力學特征的細觀參數值，直到顆粒集合表現出與實驗室測得的填土相同的宏觀性質時即可。最后，利用PFC2D程序內置的FISH語言將細觀參數賦予圖1模型并運行程序，可確定各層填土層及虛土層的初始應力σ0。標定土體細觀參數所需的宏觀參數(土體密度、壓實度、彈性模量等)參考文獻[4]，細觀參數標定結果如表1所示。

表1 土體(填土和虛土)細觀參數

考慮到實際明洞地基一般由鋼筋混凝土澆筑而成，變形相對于土體要小得多，可將其視為剛性。根據文獻[13]的經驗，采用wall單元模擬明洞地基時，切向與法向剛度可取為1.0×1010N/s；而邊坡一般經過加固處理，墻體剛度取為土顆粒剛度的10倍。故除土體外，未考慮其他材料的固結蠕變特性。

在確定Burgers本構模型的宏觀參數時，首先對文獻[4]中含水率ω=15.7%，壓實度分別為k1=96%、k2=85% 的黃土在不同加載等級下進行一維固結壓縮試驗記錄的應變—時間曲線進行擬合，得到一組宏觀參數(EM、ηM、EK、ηK)作為基礎；然后對初始宏觀參數進行數值內插，并根據前述確定的各層填土和虛土層的初始應力σ0得到對應的初始宏觀參數。

考慮土體固結蠕變的細觀參數的標定，以填土為例詳述如下：①將前述確定的各層填土的初始應力σ0及對應的宏觀參數(EM、ηM、EK、ηK)代入Burgers本構方程[式(1)]，確定各層填土固結蠕變達到穩定時的理論應變值ε0；②建立蠕變參數標定數值模型標定填土固結蠕變時的細觀參數，即：根據經驗先假定一組細觀參數作為參照賦予填土并運行PFC2D程序；運用“試錯法”不斷調整細觀參數值，直到樣本在不同初始應力σ0下的時間—應變曲線在經歷初期的瞬時彈性變形階段后平緩延伸，曲線的峰值應變ε1與理論值ε0基本相符，應變速率趨近于0，此時認為填土固結蠕變達到基本穩定。各層填土及虛土固結蠕變的細觀參數如表2所示。部分土層蠕變細觀參數的標定曲線如圖3所示。

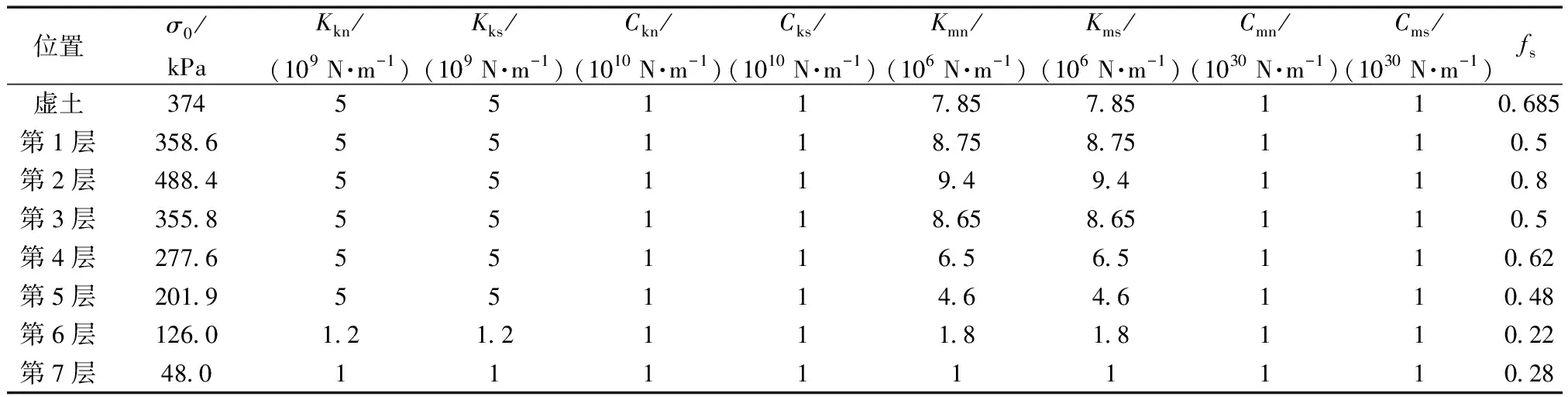
表2 土體(填土和虛土)固結蠕變的細觀參數

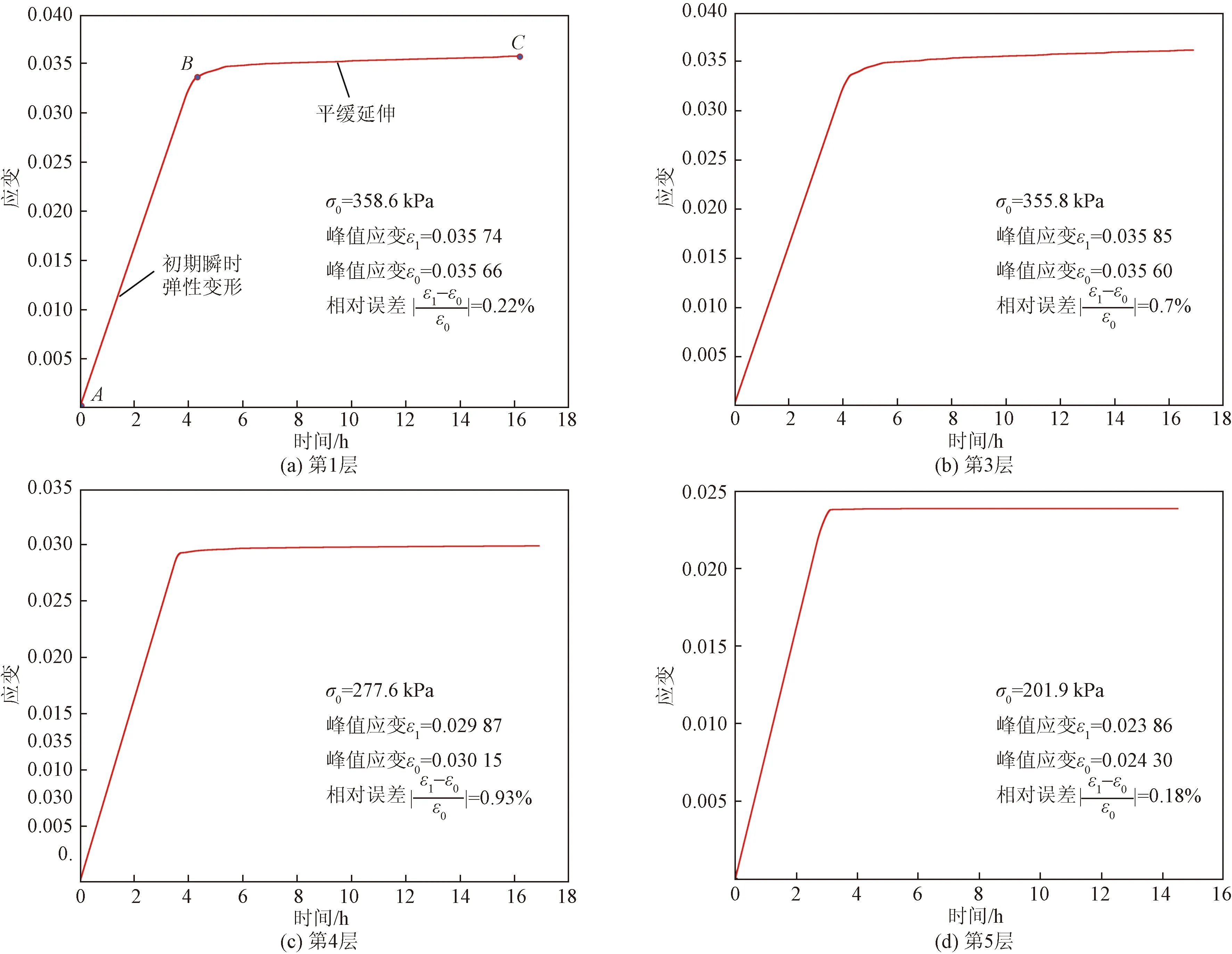
圖3 填土部分標定曲線

2 高填減載明洞土體固結蠕變結果分析

根據圖2布置的測量圓，對土體處于不同固結蠕變階段[Stage 0(S0)～Stage 10(S10)]時，明洞頂的豎向土壓力、不同填方深度處的豎向土壓力、豎向位移及填土表面沉降進行監測，結果如圖4～圖9所示。

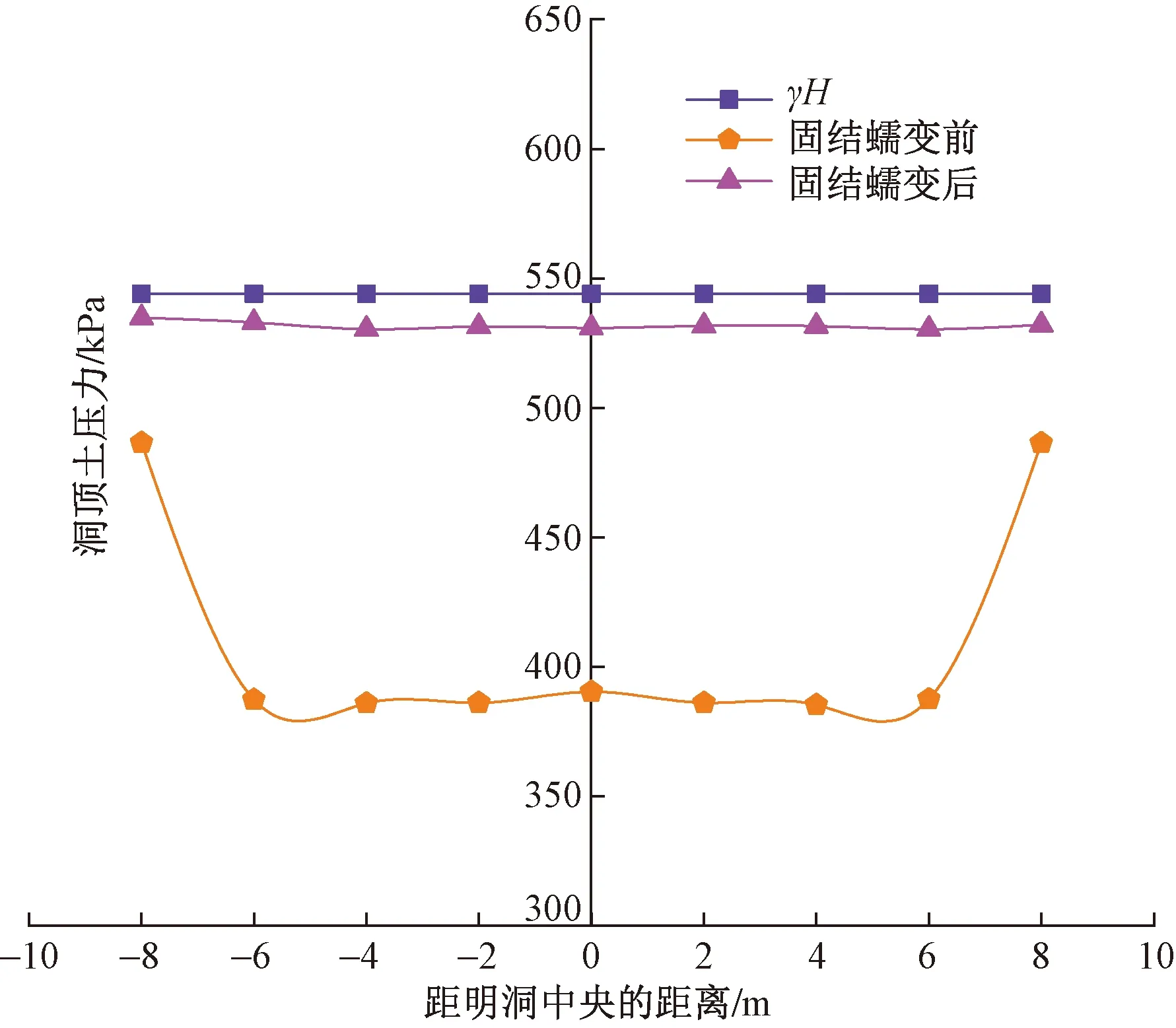
圖4 洞頂豎向土壓力

2.1 洞頂豎向土壓力分析

由圖4可知，填方完成時刻，明洞洞頂(5號測量圓處)豎向土壓力為390.4 kPa，相比豎向靜止土壓力(γH= 544 kPa，其中，γ為填土容重，H為填土表面至明洞頂的距離)減載效果明顯，減載率為28.2%；虛土寬度范圍內(1～9號測量圓)的平均豎向土壓力為386.9 kPa，平均減載率為29.0%。這是由于明洞頂設置了壓實度相對較小的虛土，其顆粒結構較為松散，壓縮性較兩側填土更大，在上層土體荷載作用下，較容易產生豎向變形，從而使內外土柱之間產生沉降差，激發了土拱效應，致使明洞洞頂上方土體荷載轉移向明洞兩側。而伴隨著土體固結蠕變的發展，虛土顆粒間有效應力增加，宏觀表現為虛土被逐漸壓實，壓縮性減小，內外土柱沉降差降低，土拱效應被削弱。此時，洞頂豎向土壓力又回調增大至約530 kPa，相比豎向靜止土壓力(γH=544 kPa)僅相差2.57%，說明固結蠕變的發展明顯削弱了虛土的減載效果。

2.2 不同填方深度處豎向土壓力分析

圖5為C-C截面和D-D截面不同填方深度處土壓力隨土體固結蠕變的變化，S0階段代表填方完成時刻。由圖5(b)可知，各層土體的初始土壓力(S0階段)均小于豎向靜止土壓力γH，也小于圖6(a)中對應位置的初始土壓力，且隨著土體的固結蠕變呈現出“先上升(S0～S2階段)、后回調(S2～S3階段)、最終穩定(S3～S10階段)”的特征。原因如下。

圖5 截面豎向土壓力

(1)填方完成時刻，C-C截面的虛土具有減載作用。但由于土體固結蠕變速率在填方完成后的初期(S0～S2階段)發展較快，土體內部顆粒間有效壓力迅速增大，虛土密實度增加，減載效果被削弱，致使明洞洞頂土壓力顯著上升。同時對比圖1分析可知，土層位置越低，上覆填方高度越大，所受上覆土體豎向荷載更大，固結蠕變也更加顯著，因而位置較低的土層較位置較高處的土層豎向土壓力增加明顯。

(2)土壓力達到峰值后回調(S2～S3階段)是由于虛土的殘余減載效果被增大的土壓力進一步激發導致的，但由于此時虛土的密實度增加，其殘余減載效果有限，故而土壓力的回調程度較小，且由于土層位置越高，其上覆填方高度越小，所受上覆土體豎向荷載相對較小，故回調趨勢的變化也隨土層位置由低處向高處逐漸遞減；S3～S10階段，土壓力變化基本穩定，說明土體的固結蠕變在S3階段以后趨于穩定。圖5(b)表明，由于D-D截面處于虛土外側，填土土壓力未受到虛土殘余減載效果的影響，且由于壓實度較大，固結蠕變階段(S3～S10階段)各層土壓力逐漸增加，至S3階段以后也達到穩定。

2.3 不同填方深度處豎向位移分析

圖6為C-C截面、D-D截面不同填方深度處豎向位移隨土體固結蠕變的變化規律。對比圖5可知，各層土體豎向位移的變化規律與土壓力的變化相對應，C-C截面豎向位移隨土體的固結蠕變同樣呈現出“先上升(S0-S2階段)、后回調(S2～S3階段)、最終穩定(S3～S10階段)”的特征；D-D截面豎向位移則持續增加，且各層土體豎向位移在S3階段以后基本穩定。同時可以看出，在固結蠕變初期，由于虛土壓實度較低，壓縮變形明顯，故C-C截面各層的豎向位移增量相較D-D截面對應各層較大。而隨著土壓力的回調[圖5(a)中S2～S3階段]，土顆粒之間咬合嵌套作用減弱，顆粒體系無法保持原有狀態下的平衡而自發的調整相對位置，產生相互滑移、錯動。故而C-C截面處土體各層豎向位移也在S2～S3階段出現小幅回調。

2.4 填土表面沉降分析

填土表面沉降是表層填土豎向位移和低處土層豎向位移共同累積的結果。圖7為圖2中B-B截面布設的位移測量圓監測的土體(填土和虛土)固結蠕變前后填土表面沉降變化的對比情況。可以看出，填方完成時刻，填土表面沉降量較小且分布均勻，平均沉降量僅為35.4 mm；當固結蠕變基本穩定時，填土表面沉降量相較于填方完成時顯著增加，且由于虛土的存在，洞頂寬度范圍正上方的填土表面累積沉降量最大(830 mm)，最小沉降量(600 mm)則分布在兩側，總體呈現出“中間大，兩頭小的特征”。由固結蠕變引起的沉降量分別占累積沉降量的95.7%和94.1%。填土表面沉降量隨固結蠕變的持續增大將對土體內部土壓力環境的穩定性產生擾動，并對明洞襯砌結構產生危害。

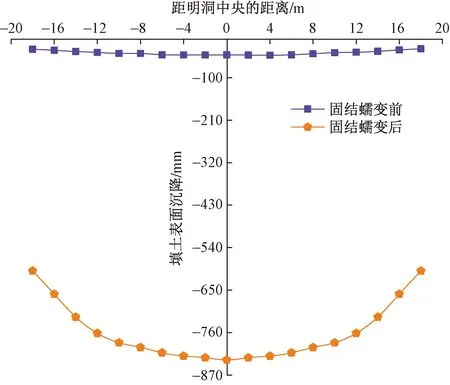
圖7 填土表面沉降

2.5 接觸力鏈分析

在PFC2D中，接觸力鏈(contact force chain)的分布實質上反映了土體中荷載的傳遞，力鏈的細密程度代表土顆粒間接觸力的大小，線條組成的網絡結構代表接觸力的分布集度和荷載傳遞方向，網絡結構越密集說明顆粒接觸越緊密。

圖8(a)～圖8(c)為顆粒間接觸力鏈伴隨土體固結蠕變的細觀演化過程。分析圖8(a)可知：填方完成時刻(S0階段)，由于虛土的壓實度較小，結構松散，土顆粒相互之間接觸較弱，故而力鏈網絡稀疏且與周圍填土的力鏈網絡界限分明；其與兩側填土的剛度差異激發了土拱效應，從而使虛土上方的土體荷載逐漸向兩側轉移并向下傳遞，降低了洞頂承受的土壓力。虛土上方土體顆粒間的接觸力鏈呈“拱形”，其在虛土兩側分布密集、稠密而在虛土寬度范圍內分布稀疏也從細觀層面與這種荷載傳遞規律相對應。

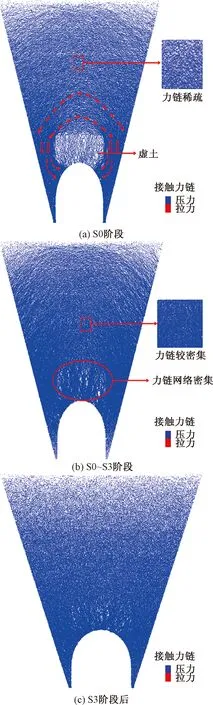
圖8 顆粒間接觸力鏈分布

圖8(b)表明：隨著土體固結蠕變的發展(S0～S3階段)，虛土與兩側填土顆粒間的接觸顯著增強，力鏈線條由圖8(a)中的“細而稀疏”變為“粗且密集”，并向兩側延伸，分布于虛土上方的“土拱”形態逐漸消失，說明土體的固結蠕變使虛土與兩側填土間的剛度差異降低，虛土顆粒被壓密。圖8(c)為土體固結蠕變趨于穩定時(S3階段之后)的接觸力鏈圖。可以看出，此時虛土上方土體顆粒間力鏈的“土拱”形態已經消失，各層土體接觸力鏈分布更加均勻。虛土范圍內顆粒間接觸力鏈更加緊密，顆粒間的接觸力增大。說明土體的固結蠕變使虛土的減載效果大幅降低，由虛土激發的土拱效應被嚴重削弱。這與圖4分析的減載明洞洞頂宏觀土壓力的變化規律相一致。

3 高填減載明洞土體固結蠕變影響因素分析

為方便設計者采取合理的設計參數優化明洞設計，以圖1建立的數值模型(T=5.0 m；W=12.8 m；f/b=0.5，其中f為矢高)為參考，分別增設虛土厚度T= 3 m(1/10H1)、4 m(1/7.5H1)、6 m(1/5H1)；寬度W= 6.4 m(0.5b)、19.2 m(1.5b)；矢跨比分別為0.4、0.6、0.7，從洞頂平均豎向土壓力(圖2中A-A截面1～9號測量圓)、填土表面沉降的角度進一步探討虛土的厚度T、長度W和明洞結構尺寸等參數變化對土體固結蠕變的影響。矢跨比f/b定義為明洞拱形襯砌的矢高f與跨徑b之比。

3.1 虛土厚度的影響

圖9為不同虛土厚度T減載時，洞頂平均豎向土壓力和填土表面沉降的分布。分析圖9(a)可知，填方完成時刻，洞頂平均豎向土壓力隨T的增大而減小，且差值顯著。這是因為T越大，土顆粒間的空隙越多，壓縮儲備空間增大，激發的土拱效應越強，減載效果更好。隨著土體固結蠕變趨于穩定，虛土被逐漸壓密，土拱效應減弱，不同虛土厚度T減載下的豎向土壓力均回調增大，洞頂平均豎向土壓力也接近γH(544 kPa)，但相對大小仍與填方完成時刻一致，說明T越大，虛土經土體固結蠕變后的殘余減載效果越大。

由圖9(b)可知，填方完成時刻不同虛土厚度T減載時，填土表面沉降均較小且分布均勻，明洞頂正上方最大沉降量在39.43～41.84 mm。土體的固結蠕變使填土表面沉降大幅增加，且T越大，虛土壓縮變形越大，各層回填土的沉降也隨之增大，最終填土表面的沉降也隨T的增大而增加。綜上分析可知，高填黃土減載明洞考慮固結蠕變時，虛土厚度T越大，殘余減載效果越佳。但在實際工程中，應綜合考慮明洞頂以上填土高度、工程實際要求等選擇適宜的虛土厚度。可得虛土厚度T=6.0 m(1/5H2)時最優。

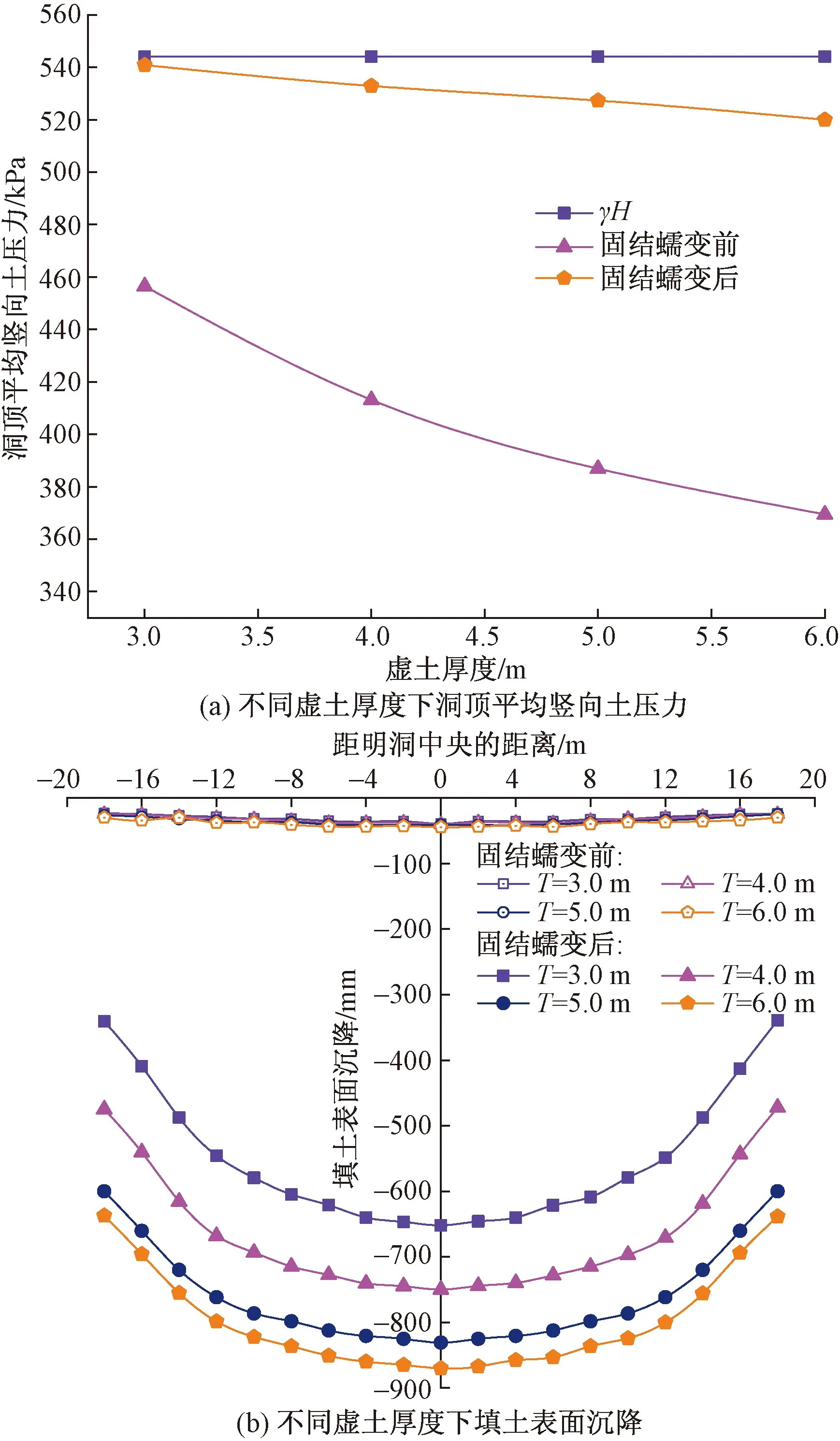
圖9 虛土厚度對下洞頂平均豎向土壓力及填土表面沉降的影響

3.2 虛土寬度的影響

圖10為不同虛土寬度W減載時，洞頂平均豎向土壓力和填土表面沉降的分布。分析圖10(a)可知，填方完成時刻，當W=6.4 m(0.5b)小于明洞寬度(b=12.8 m)時，通過虛土的減載作用向兩側轉移的上覆土體荷載仍有部分作用于洞頂，相比W=12.8 m(1.0b)和W=19.2 m(1.5b)時上覆土體荷載完全轉移向明洞寬度外側，洞頂平均豎向土壓力較大。此外，W=19.2 m(1.5b)時，由其激發的土拱被分布在更大的范圍，減載范圍擴大，反而降低了虛土的減載效率，故而洞頂平均豎向土壓力隨W的增大先減小，后小幅增大。隨著土體固結蠕變趨于穩定，洞頂豎向土壓力又回調增大，W=0.5b、1.0b、1.5b時對應洞頂平均豎向土壓力較填方完成時刻均顯著增大，分別為537.8、525.3、526.1 kPa，此時由于虛土的減載效果大幅減弱，土壓力的差異主要受土體自重荷載的影響，即在洞寬范圍內，當W=6.4 m(0.5b)時，平均豎向土壓力是虛土和部分填土自重共同作用的結果，較W=12.8 m(1.0b)和W=19.2 m(1.5b)時荷載全部源于虛土更大。綜上所述可知，填方完成時刻，虛土寬度W=12.8 m(1.0b)時減載效果較好；土體固結蠕變趨于穩定時，W=12.8 m(1.0b)的洞頂平均豎向土壓力亦相對較小。

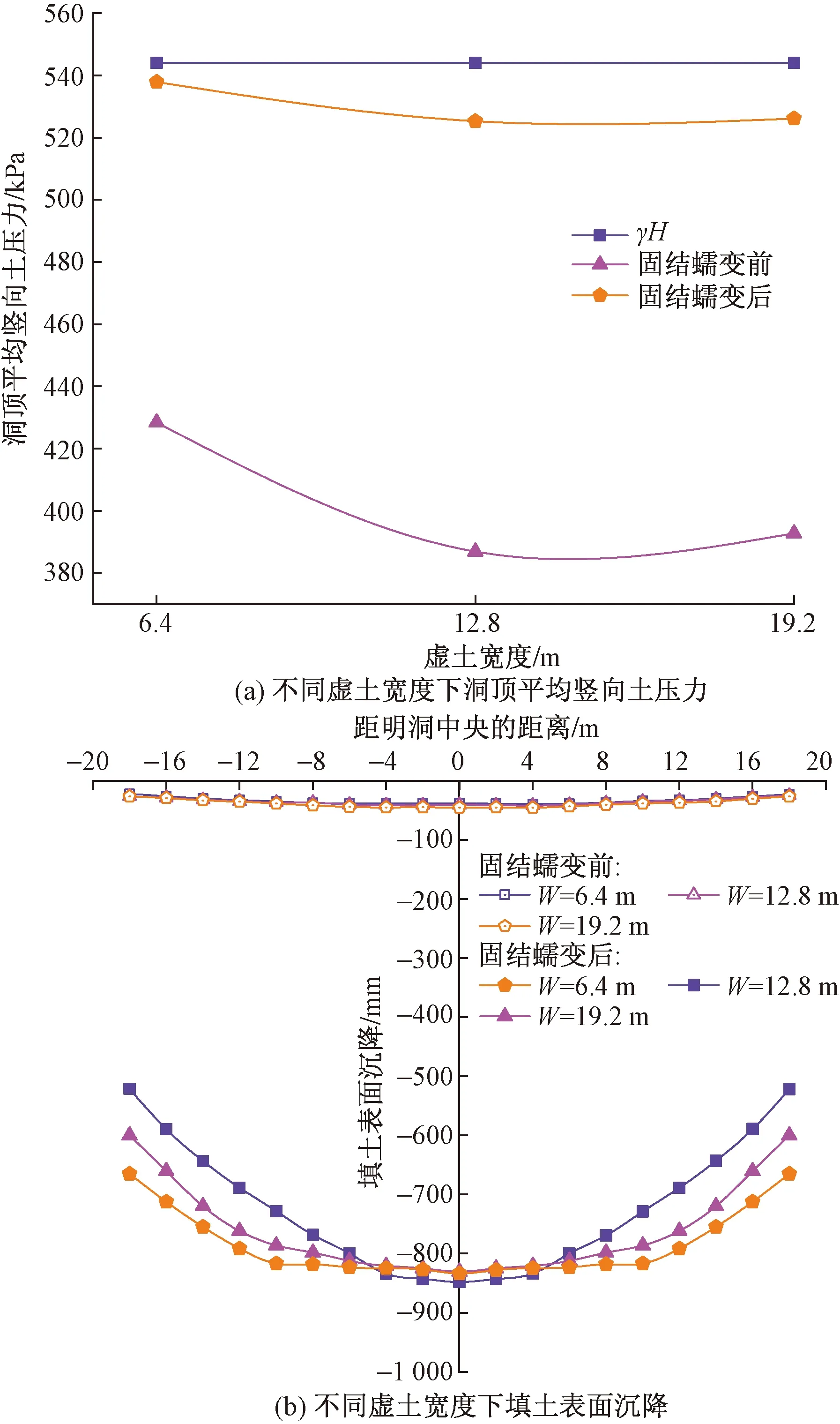
圖10 虛土寬度對洞頂平均豎向土壓力及填土表面沉降的影響

由圖10(b)可知，虛土寬度W由6.4 m(0.5b)增大至19.2 m(1.5b)時，伴隨著土體的固結蠕變，填土表面沉降較填方完成時刻均顯著增大，但數值接近，明洞頂正上方對應最大沉降量分別為844.5 mm、833.9 mm、836.6 mm，平均沉降838.3 mm，最大沉降差7.9 mm，僅占平均沉降量的0.94%，W的增大并未提高其豎向可壓縮性，而是使填土表面發生顯著沉降的范圍進一步擴大。

3.3 矢跨比的影響

圖11為矢跨比f/b分別為0.4、0.5、0.6、0.7時洞頂平均豎向土壓力和填土表面沉降的分布。分析圖11(a)可知，填方完成時刻，不同矢跨比f/b下洞頂平均豎向土壓力均在386.7 kPa。這表明虛土緊鄰明洞頂布置時，其減載作用消解了f/b變化對洞頂豎向土壓力的影響。隨著土體固結蠕變，土拱效應被削弱，不同矢跨比f/b對應的洞頂平均豎向土壓力相較填方完成時刻均回調增大，總體上隨f/b的增大逐漸減小，這主要是因為當明洞頂以上填土高度H1不變時，f/b的增大導致上覆回填土高度降低，覆土荷載減小。由圖11(b)可知，無論填方完成時刻或土體固結蠕變趨于穩定，不同矢跨比f/b時填土表面沉降曲線分布均具有較高的重合。綜上所述，無論是否考慮回填土的固結蠕變作用，采用虛土減載的高填黃土明洞矢跨比f/b的變化對填土表面沉降幾乎沒有影響。

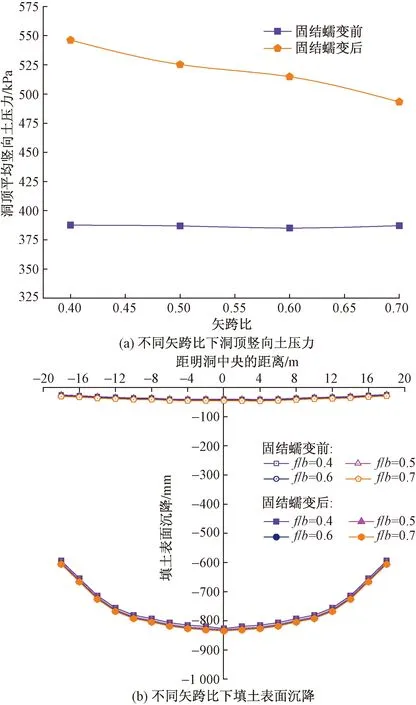
圖11 矢跨比對洞頂豎向土壓力及填土表面沉降的影響

4 結論

為探究黃土的固結蠕變對高填減載明洞長期土壓力分布及虛土減載實際效果的影響，本文利用PFC2D建立數值模型，研究了伴隨土體的固結蠕變，虛土的減載效果、不同填方深度處土壓力及豎向位移的發展規律；通過土顆粒接觸力鏈的演化規律，從細觀層面對黃土固結蠕變過程中土顆粒間的接觸變化、荷載傳遞機理進行分析；并從洞頂平均豎向土壓力、填土表面沉降的角度探究了虛土厚度T、寬度W和明洞矢跨比f/b等的變化對考慮土體固結蠕變條件下明洞受力的影響。得出如下結論。

(1)高填黃土明洞采用虛土減載能夠降低明洞洞頂豎向土壓力。但當土體固結蠕變達到基本穩定時，虛土的減載能力會明顯降低，洞頂土壓力值將回調至接近靜土壓力γH。故在進行高填黃土減載明洞的承載能力設計時，應充分考慮由黃土固結蠕變導致的減載明洞洞頂土壓力回調及其對明洞襯砌結構的影響。

(2)土顆粒間接觸力鏈的演化規律從細觀層面表明了虛土的減載效果隨土體的固結蠕變被削弱，其上方的“土拱”逐漸消失是因為：土體的固結蠕變使虛土顆粒間的接觸力鏈由疏變密，由細變粗，并與兩側填土顆粒間的接觸增強，剛度差異降低，土拱效應明顯減弱。當土體固結蠕變達到基本穩定時，土顆粒間的應力分布趨于均勻。土體的固結蠕變將使填土表面沉降持續增加，沉降增量將達累積總沉降的90%以上。

(3)明洞虛土厚度T越大，減載效果越好；土體固結蠕變后，其殘余減載效果與T的大小呈正相關。填土表面沉降亦隨T的增大而增加，最佳厚度為T=6.0 m(即1/5H1)；填方完成時刻，洞頂豎向平均土壓力隨虛土寬度W的增大先減小后增大，填土表面沉降均較小；土體固結蠕變后，不同W減載下的平均豎向土壓力差值顯著減小，填土表面沉降的范圍隨W的增大而增大，最佳寬度為W=12.8 m(即1.0b)；虛土的減載作用會抵消f/b變化對洞頂豎向土壓力的影響；土體固結蠕變后，洞頂平均豎向土壓力隨f/b的增大而減小，f/b變化對填土表面沉降幾乎沒有影響。