多解思維,多層拓展,多向歸納
——以2021年高考數學新高考Ⅰ卷第15題為例
?山東省淄博第七中學 孫麗云
函數的最值問題,一直是高考中比較常見的一類題型,背景新穎,創新多變.此類問題可以選擇題或填空題的形式出現,也可融入解答題中,形式多樣.既可以基本初等函數的組合形式來設置,也可與其他數學知識的交匯與融合來設置,變化多端.具體破解時,思維多樣,方法多變,可以很好地考查學生的數學知識、數學思想方法和數學能力等,充分體現高考的選拔性與區分度.
1 真題呈現
高考真題(2021年高考數學新高考Ⅰ卷第15題)函數f(x)=|2x-1|-2lnx的最小值為______.
2 真題剖析
該題題目簡潔明了,條件簡單易懂,以一個“一次函數的絕對值”與一個“對數函數”的差式來建立相應的函數,進而確定該函數的最小值.以簡單條件進行復合與提升.
破解本題的思維各異,方法多樣,可以通過去絕對值符號進行分類討論,結合函數的單調性來確定相應的最小值;也可以借助函數圖象,通過數形結合并利用導數的幾何意義加以求解;還可以借助“對數不等式”的重要結論合理放縮,巧妙轉化,利用不等式的性質加以處理等.
3 真題破解
方法1:分類討論法.
解析:函數f(x)=|2x-1|-2lnx的定義域為(0,+∞).
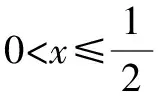
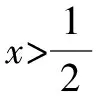
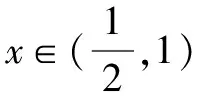
所以當x=1時,f(x)取得極小值為f(1)=2×1-1-2ln 1=1.
而2ln 2=ln 4>ln e=1,所以函數f(x)在x=1時取得最小值,且最小值為1.
故填答案:1.
點評:根據函數的解析式確定函數的定義域,結合絕對值定義對自變量x進行分段處理,進而分類討論.一方面直接利用函數的單調性來確定極值,另一方面通過對函數求導,結合函數的單調性來確定相應的極值,最后再確定函數的最小值.分類討論法綜合了函數的單調性、導數及其應用等.
方法2:導數的幾何意義法.
解析:令f(x)=0,可得|2x-1|=2lnx.
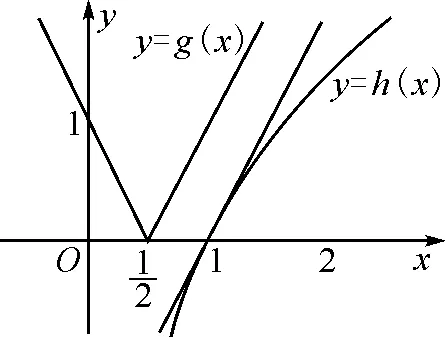
圖1
在同一平面直角坐標系中,作出函數g(x)=|2x-1|,h(x)=2lnx的圖象,如圖1所示.
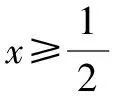
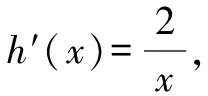
所以當x=1時,函數f(x)=|2x-1|-2lnx取得最小值f(1)=|2×1-1|-2ln 1=1.
所以函數f(x)=|2x-1|-2lnx的最小值為1.
故填答案:1.
點評:根據函數與方程的轉化,將題目條件中的函數解析式轉化為兩個基本初等函數,通過作出對應函數的草圖,數形結合確定函數取得最小值時的情形,結合導數的幾何意義,進而求解對應的最小值.利用數形結合法,在考試中只能作出簡單的草圖,加以直觀想象,巧妙應用.
方法3:重要結論法.
解析:根據“對數不等式”的重要結論“lnx≤x-1,當且僅當x=1時等號成立”,可知
f(x)=|2x-1|-2lnx≥|2x-1|-2(x-1)≥(2x-1)-2(x-1)=1.
當且僅當x=1且2x-1≥0,即x=1時等號成立.
所以函數f(x)=|2x-1|-2lnx的最小值為1.
故填答案:1.
點評:“對數不等式”的重要結論作為一個基本結論,在一些小題(選擇題或填空題)中可以直接應用,利用其來合理放縮,化歸轉化,巧妙應用,是破解一些相關不等式問題比較常用的手段.“對數不等式”這一重要結論,作為課外知識的提升與拓展,有必要對其加以理解與掌握.
4 變式拓展
通過適當改變條件,以不同的形式來巧妙設置問題,得到以下對應的變式問題.
變式1函數f(x)=x2-2lnx的最小值為______.
解析:函數f(x)=x2-2lnx的定義域為(0,+∞).
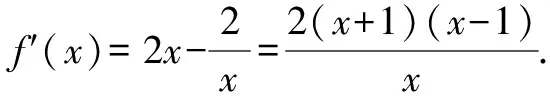
當x∈(0,1)時,f′(x)<0,f(x)單調遞減;當x∈(1,+∞)時,f′(x)>0,f(x)單調遞增.
所以當x=1時,f(x)取得最小值,且最小值為f(1)=12-2ln 1=1.故填答案:1.
變式2已知函數f(x)=ax2-x+lnx,當x≥1時,試求函數g(x)=|f(x)-2lnx|的最小值.
解析:g(x)=|f(x)-2lnx|=|ax2-x-lnx|.
可設函數h(x)=ax2-x-lnx,x≥1.

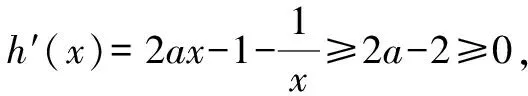
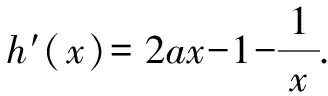
綜上可得,當a≤0時,函數g(x)的最小值為1-a;當a≥1時,函數g(x)的最小值為a-1;當0 破解函數的最值問題常見的思維方法主要有以下幾種: (1)導數方法領銜 通過對函數進行求導運算,結合導函數零點的確定,利用導函數的正負取值情況確定函數的單調性,進而確定對應的極值,從而確定函數的最值問題.直接通過導數運算,可以解決一些熟悉或不熟悉的函數問題,合理求導,以代數運算代替邏輯推理,通過運算來分析與判斷. (2)數形結合判斷 通過作出相應函數的圖象,結合函數的圖象與性質來分析與處理.利用數形結合判斷函數的最值問題時,必須是一些常見的基本初等函數,或一些熟悉的特殊函數,或把不熟悉的函數合理分解并轉化為熟悉的函數后再數形結合.對于復合類或不熟悉的函數類型,無法借助圖象來數形結合處理. (3)不等式性質放縮 在具體解決一些特殊函數的最值問題時,有時根據函數的對應關系式的特征,借助基本不等式或柯西不等式、不等式性質以及特殊的不等式,如上面提到的“對數不等式”的重要結論等,也可以很好地處理函數的最值問題. 函數最值問題的求解,借助合理的代數運算與變形,結合通分、因式分解、配湊、平方、配方、構造等運算手段加以輔助處理,或導數方法領銜,或數形結合判斷,或不等式性質放縮等,全面促進數學知識的理解與掌握,有效提高數學能力,提升數學品質,培養數學核心素養.5 解后反思

