2022年北京高考導(dǎo)數(shù)壓軸題解答
?北京市懷柔區(qū)第一中學(xué) 于海龍
1 試題呈現(xiàn)
(2022年北京高考數(shù)學(xué)第20題)已知函數(shù)f(x)=exln (1+x).
(Ⅰ)求曲線y=f(x)在點(diǎn)(0,f(0))處的切線方程;
(Ⅱ)設(shè)g(x)=f′(x),討論函數(shù)g(x)在[0,+∞)上的單調(diào)性;
(Ⅲ)證明:對(duì)任意的s,t∈(0,+∞),有f(s+t)>f(s)+f(t).
2 解法分析及詳解
2.1 第(Ⅰ)問(wèn)的解答
本小題求曲線y=f(x)在點(diǎn)(0,f(0))處的切線方程,先求f′(x),得f′(0)即為曲線在點(diǎn)(0,f(0))處的切線的斜率,進(jìn)而求出切線方程.

又因?yàn)閒(0)=0,f′(0)=1,所以曲線y=f(x)在點(diǎn)(0,f(0))處的切線方程為y=x.
2.2 第(Ⅱ)問(wèn)的解答
本小題討論函數(shù)g(x)在[0,+∞)上的單調(diào)性,依題意有如下兩種解法,如圖1所示.
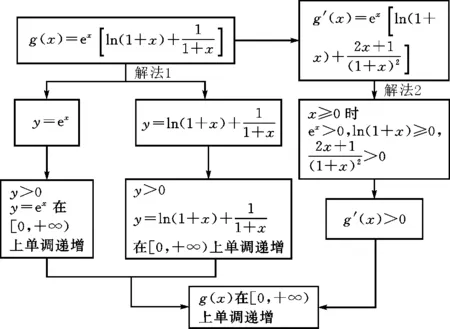
圖1
思路一:根據(jù)導(dǎo)數(shù)與函數(shù)單調(diào)性的關(guān)系,通過(guò)導(dǎo)函數(shù)的正負(fù)研究函數(shù)的單調(diào)性.若導(dǎo)函數(shù)無(wú)變號(hào)零點(diǎn),則可判斷導(dǎo)函數(shù)恒正或恒負(fù)的情況.
解法1:通法——從導(dǎo)數(shù)入手.


所以函數(shù)g(x)在[0,+∞)上單調(diào)遞增.
思路二:研究復(fù)雜函數(shù)的單調(diào)性,可以將復(fù)雜的函數(shù)分解,研究局部性質(zhì),通過(guò)整合,依托單調(diào)性定義,借助不等式的性質(zhì)解決問(wèn)題.
解法2:分解函數(shù),依托不等式性質(zhì)與單調(diào)性定義.
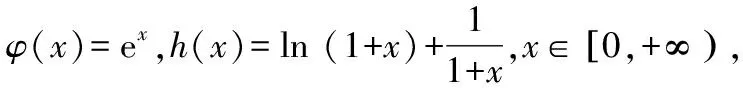
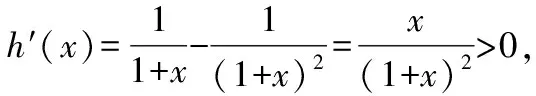
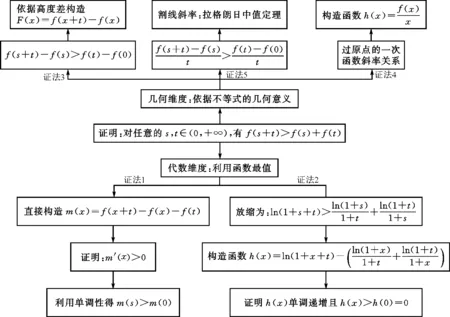
又因?yàn)棣?x)在[0,+∞)上單調(diào)遞增,且φ(x)>0,所以?x1,x2∈[0,+∞)且x1 φ(x2)>φ(x1)>0,h(x2)>h(x1)>0, 所以φ(x2)h(x2)>φ(x1)h(x2),即g(x2)>g(x1). 故函數(shù)g(x)在[0,+∞)上單調(diào)遞增. 本小題的本質(zhì)是研究函數(shù)的最值問(wèn)題.依題意有如下三類(五種)證明方法,如圖2所示. 圖2 思路一(代數(shù)維度):本題所證不等式中有兩個(gè)變量,兩側(cè)均有相同的變量,故需要選擇其中一個(gè)為主元進(jìn)行研究,從而構(gòu)造函數(shù),通過(guò)最值證明不等式. 證法1:常規(guī)方法——選擇主元,直接移項(xiàng)構(gòu)造新函數(shù). 令m(x)=f(x+t)-f(x)-f(t)=ex+t·ln (1+x+t)-exln (1+x)-etln (1+t)(x>0),則 因?yàn)閠>0,則et>1,且ex≥1+x恒成立,所以 因此m(x)在[0,+∞)上單調(diào)遞增. 再由s>0,得m(s)>m(0),即f(s+t)-f(s)-f(t)>f(0+t)-f(0)-f(t)=-f(0). 由f(0)=0,得f(s+t)-f(s)-f(t)>0. 所以f(s+t)>f(s)+f(t)成立. 事實(shí)上,證法1可以優(yōu)化: 令m(x)=f(x+t)-f(x)-f(t)(x>0),則 m′(x)=f′(x+t)-f′(x)=g(x+t)-g(x). 由(Ⅱ)中g(shù)(x)在[0,+∞)上單調(diào)遞增,則由t>0得s+t>s,從而g(x+t)>g(x)即m′(x)>0. 因此m(x)在[0,+∞)上單調(diào)遞增. 再由s>0,得m(s)>m(0),即f(s+t)-f(s)-f(t)>f(0+t)-f(0)-f(t)=-f(0). 由f(0)=0,得f(s+t)-f(s)-f(t)>0. 所以f(s+t)>f(s)+f(t)成立. 思路二(代數(shù)維度):在指數(shù)式與對(duì)數(shù)式共存的前提下,借助已有的結(jié)論“ex≥x+1;x-1≥lnx”等合理放縮再構(gòu)造函數(shù)進(jìn)行證明. 證法2:合理放縮——借助于常見(jiàn)的函數(shù)大小關(guān)系的結(jié)論合理放縮,再構(gòu)造函數(shù)進(jìn)行證明. 要證對(duì)任意的s,t∈(0,+∞),有f(s+t)>f(s)+f(t),即證明對(duì)任意的s,t∈(0,+∞),有 es+tln (1+s+t)>esln (1+s)+etln (1+t). 即只需證明 因?yàn)閑x≥1+x恒成立,所以只需證明 所以h(x)在(0,+∞)上為增函數(shù). 所以原式f(s+t)>f(s)+f(t)成立. 思路三(幾何維度):依據(jù)不等式本身結(jié)構(gòu)上蘊(yùn)含的特征,可以轉(zhuǎn)化為函數(shù)圖象中縱坐標(biāo)的差值,通過(guò)調(diào)整結(jié)構(gòu),從而抽象出新的函數(shù). 證法3:特殊方法——依托結(jié)構(gòu)特征,等價(jià)轉(zhuǎn)化,構(gòu)造新函數(shù). 由(Ⅰ)中f(0)=0,將原待證不等式轉(zhuǎn)化為證明f(s+t)-f(s)>f(t)-f(0). 令F(x)=f(x+t)-f(x),則F(s)=f(s+t)-f(s),F(0)=f(t)-f(0). 因?yàn)镕′(x)=f′(x+t)-f′(x)=g(x+t)-g(x),且由(Ⅱ)中g(shù)(x)為增函數(shù),所以在t>0時(shí)可得F′(x)>0. 于是F(x)為增函數(shù).則由s>0,得F(s)>F(0),即f(s+t)-f(s)>f(t)-f(0). 所以f(s+t)>f(s)+f(t)成立. 思路四(幾何維度):類比不等式f(s+t)>f(s)+f(t)與過(guò)原點(diǎn)的一次函數(shù)模型f(x+y)=f(x)+f(y)相似的特征,轉(zhuǎn)化為斜率關(guān)系,結(jié)合函數(shù)凹凸性,構(gòu)造增函數(shù)進(jìn)行證明. 證法4 :借助模型——依托結(jié)構(gòu)特征,構(gòu)造函數(shù). 所以φ(x)在(0,+∞)上是增函數(shù),從而φ(x)>φ(0)=0. 于是h′(x)>0,所以h(x)在(0,+∞)上為增函數(shù),則有h(s+t)>h(s),h(s+t)>h(t). 所以原式不等成立. 思路五(幾何維度):依托不等式結(jié)構(gòu)上的特征,合理變形,轉(zhuǎn)化為割線的斜率,從而應(yīng)用拉格朗日中值定理,完成證明. 證法5 :高等數(shù)學(xué)應(yīng)用——借助于高等數(shù)學(xué)知識(shí)(拉格朗日中值定理)進(jìn)行變形完成證明. 要證“對(duì)任意的s,t∈(0,+∞),有f(s+t)>f(s)+f(t)”,只需證不等式 f(s+t)-f(s)>f(t)-f(0). 由a∈(s,s+t),b∈(0,t),得a>b. 所以對(duì)任意的s,t∈(0,+∞),f(s+t)>f(s)+f(t)成立. 總結(jié)賞析:證明不等式問(wèn)題,重點(diǎn)在于等價(jià)轉(zhuǎn)化.縱觀2022年北京高考導(dǎo)數(shù)問(wèn)題解法的切入點(diǎn),不同的入手角度,概括了構(gòu)造函數(shù)的過(guò)程,即從簡(jiǎn)單的移項(xiàng)構(gòu)造函數(shù),到關(guān)注結(jié)構(gòu)特征所隱含的信息構(gòu)造函數(shù),最后到借助高等數(shù)學(xué)知識(shí)解題.這些都啟示我們?cè)诮窈蟮牡膹?fù)習(xí)過(guò)程中,理解“構(gòu)造函數(shù)”的演變過(guò)程,展望“構(gòu)造函數(shù)的發(fā)展方向,為函數(shù)與導(dǎo)數(shù)知識(shí)的復(fù)習(xí)提供參考依據(jù). 通過(guò)對(duì)2022年北京高考函數(shù)與導(dǎo)數(shù)問(wèn)題的分析,發(fā)現(xiàn)北京卷導(dǎo)數(shù)問(wèn)題題干簡(jiǎn)潔、大氣,問(wèn)題設(shè)計(jì)巧妙.各小問(wèn)題之間往往有關(guān)聯(lián)性,由淺入深,由易到難.重點(diǎn)考查導(dǎo)數(shù)的基礎(chǔ)知識(shí)和基本思想,突出考查導(dǎo)數(shù)的本質(zhì).在研究導(dǎo)數(shù)問(wèn)題的過(guò)程中,要注意關(guān)注問(wèn)題的連貫性,借助上一問(wèn)的結(jié)論解決下一問(wèn).因此,在教學(xué)中,教師要?jiǎng)?chuàng)新問(wèn)題情境,設(shè)計(jì)連貫性問(wèn)題,運(yùn)用恰當(dāng)?shù)慕虒W(xué)方式,讓學(xué)生在學(xué)習(xí)過(guò)程中不斷探索與研究、總結(jié)與反思.在落實(shí)四基的基礎(chǔ)上,發(fā)展學(xué)生的數(shù)學(xué)核心素養(yǎng),提高分析問(wèn)題和解決問(wèn)題的能力.2.3 第(Ⅲ)問(wèn)的解答


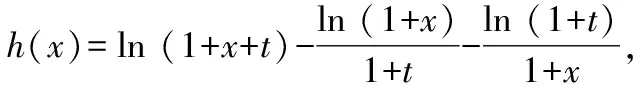



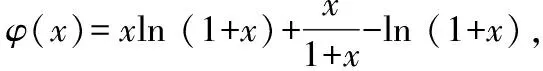
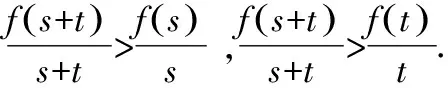

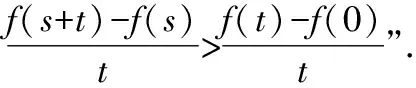

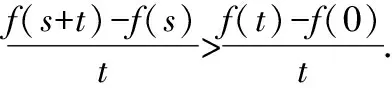
3 總結(jié)

