基于深度學習的課堂探究型教學設計*
——以“三棱錐的外接球問題”為例

?江蘇省阜寧教師發(fā)展中心 曹子清

1 引言

深度學習是基于數學學科核心內容，以發(fā)展高階思維能力為目標，學生圍繞具有挑戰(zhàn)性的學習主題進行深度探究，全身心參與學習活動，形成積極的情感、態(tài)度，獲得發(fā)展的有意義的學習過程[1].數學是思維的科學，選擇合適的數學模型表達所要解決的數學問題，通過數學學會思維，是培育數學核心素養(yǎng)的有效途徑.

深度學習是探究性學習，數學探究能促進學生養(yǎng)成必備品格、練就關鍵能力、樹立正確的價值觀.數學課堂教學，既要引導學生掌握數學知識，又要讓學生經歷數學探究過程，更要讓學生體驗隱藏在知識背后的數學思想及研究方法.《普通高中數學課程標準(2017年版)》指出：提高從數學角度發(fā)現和提出問題的能力、分析和解決問題的能力，通過高中數學課程的學習，樹立敢于質疑、善于思考、嚴謹求實的科學精神[2].在深度思考、充分參與、變式探究中，獲得數學學習的創(chuàng)新感和成就感，是數學教學的關鍵環(huán)節(jié).下面，筆者以“三棱錐的外接球問題”設計為例，談如何做好基于深度學習的課堂探究型教學設計.

2 課堂實錄及設計說明

師：三棱錐的外接球問題是一類熱點問題，對空間想象、邏輯推理能力的要求比較高.本節(jié)課，我們就此類問題進行專題研討.

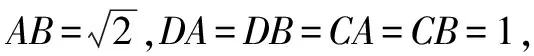
A.π B.2π C.3π D.4π

學生短暫思考后，教師隨機選取一小組上臺展示.

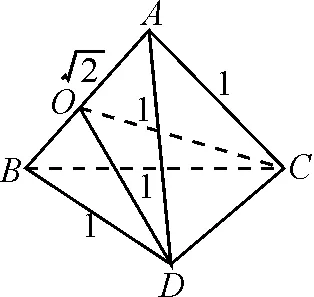
圖1

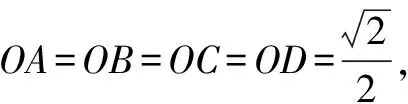
師：解答此問題的關鍵是什么？

生2：本題圖形具有明顯的特征，即四面體的兩個面是有公共斜邊的直角三角形，所以公共斜邊的中點到四面體的四個頂點距離相等，即為球心，半徑是公共斜邊的一半.

師：很好.請歸納一下該數學模型的相關結論.

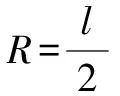
設計意圖:深度學習需要從本源性問題入手，增強學生的體驗和理解.例1圍繞研究幾何體外接球的核心元素，從學生熟知的數學模型入手，對具有明顯特征的圖形進行模型識別，有利于學生的識圖能力的提升.

師：若三棱錐有兩個側面是直角三角形，但是不共斜邊而共直角邊呢？

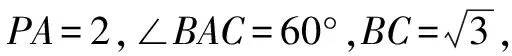
學生活動：

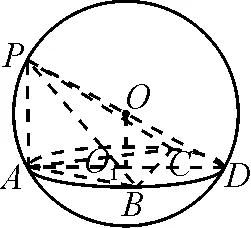
圖2

生3：(投影展示圖2)設O1為△ABC的外接圓的圓心，連接AO1并延長交外接球于點D，連接PD，過O1作AD的垂線交PD于點O，則O為外接球球心.

師：本題解題關鍵是什么？

生3：本題的解決，充分利用了球的性質，即球心與小圓的圓心連線垂直于小圓，這也是球的一個顯性幾何特征.

師：定出球心后，接下來要做什么？

生(齊聲)：求半徑.

師：請大家解答一下.

學生分小組展開討論，教師隨機選取一小組上臺展示.

師：請歸納該數學模型的相關結論.

設計意圖:深度學習倡導學生通過探究既要積累學習經驗，又要優(yōu)化思維方式，促進方法的遷移.本板塊兩個例題的設計，既有相同的要素，即共邊的兩個面都是直角三角形，又有不同的要素，相近而又相異的模型，建立起深度學習的實踐模式，讓學生在解決問題中，增強對數學本源的深刻理解.

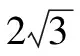
生6：應該把球心放在一個平面圖形中.

師：這位同學提供了很好的思路，空間問題應該盡可能地平面化.那么怎么確定這樣的一個平面呢？

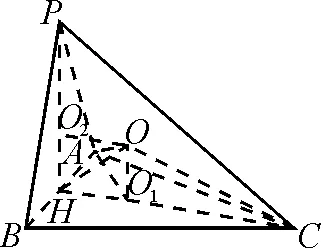
圖3

生7：(投影展示圖3)因為平面PAB⊥平面ABC，PA=PB，所以取AB的中點H，連PH，CH，設O1為△ABC外接圓的圓心，則三棱錐外接球的球心O在平面PCH內，且OO1⊥CH.

師：為什么？

生8：可證PH⊥平面ABC，OO1⊥平面ABC，所以PH∥OO1,從而球心O一定在平面PCH內.

師：非常好！但是怎樣確定球心的實際位置呢？

學生一時安靜，不知如何下手.

師：碰到困難時，不妨回到定義解題.球心的性質是什么？

生(齊答)：球心到球面上各個點的距離相等.

師：本題中，應該到三棱錐四個頂點的距離相等.

學生快速解答，教師隨機提問一小組上臺展示.

師：請歸納一下該數學模型的相關結論.

設計意圖:深度學習倡導通過探究具有挑戰(zhàn)性的問題，發(fā)展學生的高階思維.本板塊通過側面與底面關系變化，構建形成不同的模型載體，在不同的探究中獲得系統(tǒng)的研究方法.抓住球心所在的平面這一關鍵，利用平面圖形構造直角三角形進行求解，使體現學科本質、富有深度思考的學習活動真正發(fā)生.

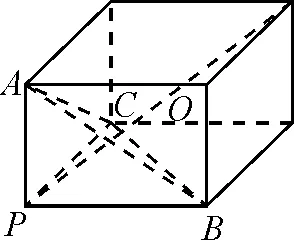
圖4

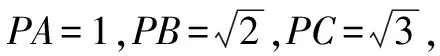
師：大家分小組研究一下.

學生分小組展開討論，教師隨機選取一小組上臺展示.

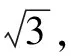
師：很好.能否告訴大家，解答此問題的關鍵是什么？

生12：圖形具有明顯的特征，即屬于三條側棱兩兩垂直的三棱錐的外接球問題，將其補形成長方體，然后找到外接球的球心即可.

師：歸納一下該數學模型的相關結論.

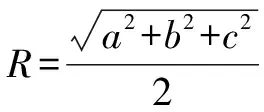
師：剛才我們研究了兩類特殊幾何體的外接球問題，那么請大家看下面一道題.

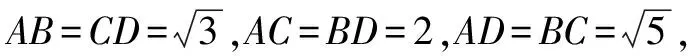
A.2π B.4π C.6π D.8π

師：大家先分小組研究一下.

學生小組展開討論，教師隨機選取一小組上臺展示.

生14：考慮到四面體ABCD的三組對棱分別相等，可將其補形成長、寬、高分別為x，y，z的長方體，則(2R)2=x2+y2+z2=6(R為球的半徑)，得2R2=3，所以球的表面積為S=4πR2=6π.

師：很好.能否告訴大家，解答此問題的關鍵是什么？

生15：圖形具有明顯的特征，即屬于三組對棱分別相等的四面體的外接球問題，將其補形成長方體，然后找到外接球的球心即可.

師：歸納一下該數學模型的相關結論.

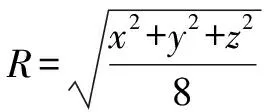
設計意圖:數學是充滿聯系的，不要教孤立的片段，應該教聯系的材料[3].深度學習通過用理解性、階梯式、探究性的問題引導學生深度思考，獲得思維的拓展.本板塊通過對三棱錐邊長關系的變化，設計形成新的圖形特征，構建新的數學模型，在問題解決中實現思維創(chuàng)新.

師(總結)：本節(jié)課研究了不同類型的三棱錐外接球問題，其關鍵是尋找球心和半徑.大家總結一下有哪些途徑？

生17：一是直接利用定義找球心，求半徑；二是將三棱錐放入特殊的幾何體中，求半徑；三是找圓心，找球心，利用直角三角形求半徑.

師：在求解的過程中要充分利用平面幾何知識尋找?guī)缀误w中元素間的關系，確定球心的位置，弄清球的半徑(直徑)與該幾何體已知量的關系，列方程(組)求解.

師：數學中有很多的模型，雖然看似并不相同，但其實有很多的關聯，我們要學會研究總結，歸類思考.

3 教學啟示

3.1 探究型設計需要選擇適切的模型載體

深度學習是一種由淺入深、由表及里、從已知到創(chuàng)新的深入探究的過程.利用基本模型，讓學生充分經歷直觀感受、批判優(yōu)化、意義聯接等學習活動，通過觀察和想象，積累活動經驗，用聯系的視野在不同維度的問題探究之間自如切換，形成積極情感體驗和高階思維能力.本節(jié)課的探究型教學設計，始終圍繞“模型分析—本質確認—意義獲得”等環(huán)節(jié)層層展開，深探究、長智慧、促思維、提學力，助推學生對三棱錐外接球問題的本質思考.因為有適切的模型載體，學生的思維策略逐步明朗且不斷深化.

3.2 探究型設計需要持續(xù)可視的思維進階

深度學習在問題情境中對知識進行批判理解、主動聯系、整合信息、遷移應用，通過有意義的系列探究問題設計，助推學生由“學科思維”走向“學會思維”，由“認同性思維”走向“批判性思維”，形成系統(tǒng)思維的結構觀念，實現思維的可視化.本節(jié)課的探究型教學設計，思考的維度和深度不斷提升，研究的途徑不斷豐富，因而創(chuàng)造思維能力、邏輯思維能力和審辨思維能力也隨之不斷提升.

3.3 探究型設計需要素養(yǎng)培育的有效增值

數學核心素養(yǎng)的提升是綜合、持續(xù)發(fā)展的過程，它需要重視單元整體知識的構建，增強知識系統(tǒng)化和結構化的網路結構意識.本節(jié)課的探究型教學設計，既有教師關鍵節(jié)點處的“導”，更有學生疑難處的“探”，更有結課時的思維導圖，新穎而不斷深入的問題情境，幫助學生確立研究問題的思維路徑，不斷地發(fā)現問題、生成問題，然后完善問題、發(fā)展問題，增強了學生學好數學的自信心和成就感.

探究型設計有助于深度教學、深度學習的開展，而強化教學設計的研究和課堂探究活動的深入展開，還需要更多的作為和實踐.