采用混沌振子和新相態判別法的局部放電檢測

李曉霞，張啟宇，馮志新，王雪

(1. 省部共建電工裝備可靠性與智能化國家重點實驗室(河北工業大學 電氣工程學院)，天津 300132；2.河北省電磁場與電器可靠性重點實驗室(河北工業大學 電氣工程學院)，天津 300132)

0 引 言

局部放電是由于電力設備內部缺陷導致電場不平衡而產生的，會使設備出現絕緣缺陷甚至擊穿。因此對設備可能出現的局部放電進行早期診斷尤為重要，利用混沌振子可以準確地判別強噪聲中微弱的局部放電信號是否存在。

利用Duffing振子[1-2]的小信號敏感性和抗噪性實現配電網的故障選線以及5次電力諧波檢測。通過設計強耦合振子[3]利用瞬態同步差值檢測微弱脈沖信號。設計新型混沌振子[4]實現更低的信噪比門限。設計三維Liu-cos混沌系統[5]配合收斂性算法實現了具有廣域性的聲波檢測并搭建了實際電路進行驗證。在研究判別系統相變狀態方面，主要有基于相位圖的相圖分割法[6]、“十字法[7]”、網格法[8]等定性地判斷系統相變狀態，采用Melnikov函數法[9]、Lyapunov指數法[10]等定量地判斷系統相變狀態；在檢測電力設備的局部放電信號的研究方面，主要有脈沖電流法[11]、超聲波法[12]、超高頻法[13]、光測法[14]等方法。

針對弱信號的檢測工作還存在著諸多困難：(1)信噪比門限偏高[1-2]；(2)需要多個振子應對初始相位未知的待測信號[15-16]；(3)相態判別方法普適性不足或實時性較差[6-10]；(4)其他局部放電檢測方法需要降頻處理以及易受噪聲影響等問題[11-14]。為此，采用新型混沌振子檢測弱信號，實現低信噪比檢測。僅使用正反相兩個系統就可以檢測任意起始相位信號。提出了具有普適性的新相變判別法，能夠實現自動識別系統相變狀態包括間歇混沌狀態，并能記錄間歇混沌狀態下的周期時長進而計算未知頻率的待測信號，還可實現變壓器局部放電的超高頻實時檢測且具備良好的抗噪性。

1 新型混沌振子檢測模型

1.1 動力學方程及抗噪性對比

新型混沌振子模型為二階非線性非自治系統，其特點為數學模型簡單，并且擁有多元化的參數形式。其動力學方程如下:

(1)

其中x,y作為狀態變量；a、b、c為系統的參數；γsin(ωt)為驅動信號。保持參數a、b、c不變，通過調整驅動信號幅值γ逐步增加，振子模型的相變狀態會相應地出現固定點、混沌、臨界混沌再到周期的變化過程，此模型存在多種參數和復雜的動力學行為。

將系統參數賦值a=2,b=10,c=1,驅動信號角頻率ω=1 rad/s，模型的起始狀態為(x,y)=(0,0)。通過改變驅動信號幅值，從而隨之發生改變的最大Lyapunov指數如圖1所示。

可以看出，混沌振子隨著驅動信號幅值的增加，系統狀態會在周期態和混沌態之間交替，利用第二個交替點作為檢測點，首先將驅動信號幅值設定為臨界混沌閾值，再加入同為正弦信號的待測信號，二者經矢量疊加后，若總的驅動信號幅值超過臨界混沌閾值，則振子模型的相態將從臨界混沌狀態突變到周期態，表明已檢測出微弱的待測信號。

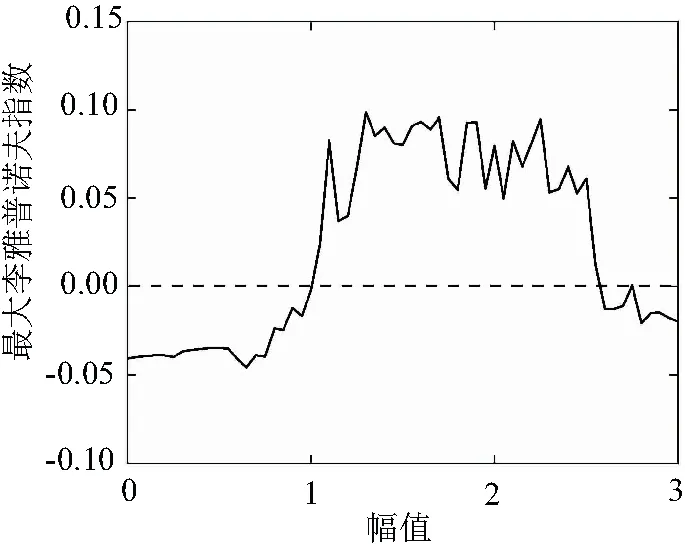
圖1 新型混沌振子的Lyapunov指數

驅動信號為周期函數的混沌振子模型具有良好的抗噪能力，因此將白噪聲引入振子模型。由此產生的擾動期望為零，整個模型依然隨著正常的相軌跡進行變化，運動中所偏離軌跡的程度由噪聲方差決定。因此，通過對比不同混沌振子在相同噪聲方差下修正作用的差異，展現不同的振子模型自身抗噪性的強弱。為了說明并量化不同振子模型對噪聲方差的修正效果，加噪與不加噪混沌振子模型的均方差為：

(2)

其中xi0(t)為不加噪聲的系統；xin(t)為加入噪聲系統。對Duffing振子、雙耦合Duffing振子和新型混沌振子進行抗噪性的對比分析如圖2所示。

圖2 三種混沌振子的均方差

上述的幾種振子模型均出現增大噪聲方差從而引起均方差的提高，其抵抗噪聲能力隨噪聲方差的增加而降低，表明混沌系統的抗噪聲能力還是會受到噪聲一定程度的干擾。但是給定同樣的噪聲方差，新型混沌振子模型的受擾動所產生的幅度更小，其次是雙耦合Duffing模型，Duffing模型受干擾最大，因此新型混沌振子在[10-3,10-1]的噪聲方差區間內的抗噪性能強于另外兩種振子模型。

1.2 待測信號的初始相位分析

由于驅動信號與待測信號很難保證相位差為零，所以討論待測信號初始相位對檢測效果的影響至關重要。首先將驅動信號初始相位置零，即δ=0°，φ∈[0°,360°]為ω=1 rad/s的待測信號初始相位，所以總驅動信號為：

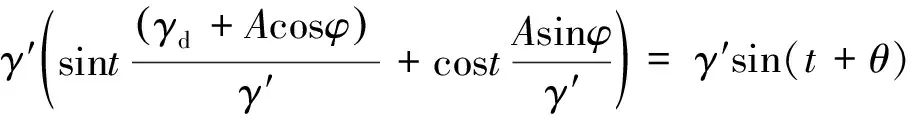
(3)

其中γd為臨界混沌閾值；A為微弱待測信號幅值；θ=arctan(Asinφ/(γd+Acosφ))。由于γd>>A，所以θ≈0°。則系統產生相變的依據為：

(4)

其中，γc是臨界周期閾值。由文獻[16]可知，分別設置三個振子驅動信號初始相位δi=0°,120°,240°(i=1,2,3)，每個振子覆蓋120°的相位范圍，就可以檢測任意初始相位的待測信號。

通過式(4)變化，可以擴大混沌振子對待測信號初始相位的覆蓋區域。

(5)

新型混沌振子可以區分的待測信號為其初始相位需要符合式(5)，由此說明混沌模型能夠區分相位范圍的因素包括臨界閾值和待測信號幅值。

首先考慮臨界閾值的影響，通過固定待測信號幅值，將驅動信號臨界閾值的精度高于待測信號幅值的精度后發現單個振子所能檢測的待測信號初始相位范圍將會擴大，其分析結果如表1所示。

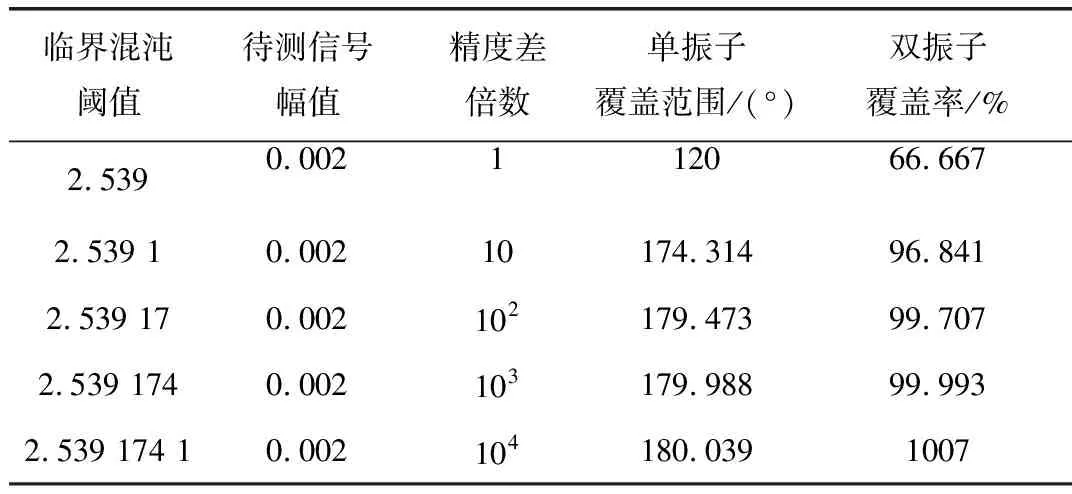
表1 不同精度差倍數下的待測信號初始相位分析

可以看到當高于102倍的精度差，利用正反相的雙振子模型可覆蓋待測信號99%范圍的初始相位；當達到104倍時，正反相的雙系統即可檢測任意相位差的待測信號。由此說明隨著驅動信號臨界混沌閾值的精度的大幅提高，可以降低振子的數量。

其次，研究待測信號的幅值。通常情況下，檢測過程前已經觀察并得出所使用的混沌振子模型的臨界閾值，因此可以對其先行設定，而待測信號幅值為不確定量，對式(3)求導可知：

(6)

f(A)為單調遞減函數，當待測信號幅值越大，就能檢測到初始相位更廣的待測信號。

綜合以上兩種因素，需要在檢測前將臨界閾值的精度盡可能地提升，使單個新型混沌振子能夠識別相差范圍擴大。

2 新相態判別法

由于相位圖或時序圖自動化識別程度不高；Lyapunov指數法或是Melnikov函數法原理復雜，實時性差；基于相位圖的方法，例如相圖分割法、網格法或是“十字法”等依賴周期態軌跡為規則圖形，且無法對間歇混沌狀態做出正確的判斷。

由此，提出能夠使計算機或電路自動識別的新相態判別法。將某一狀態變量的采樣點與延時整周期的采樣點做差，當混沌振子模型為周期狀態時，間隔整周期的采樣點近似相等差值為零；當模型為混沌狀態時，系統相軌跡將在有限的范圍內不規律運動所以表現為差值多變。即可區分系統正在處于混沌狀態還是周期狀態，也降低了振子在過渡時期的干擾因素，同時還可以判別模型的間歇混沌狀態。

首先分別對混沌及周期態進行仿真實驗，設置驅動信號角頻率ω0=1 rad/s，仿真時間T=800 s，采樣頻率fs=100 Hz，周期態仿真設置驅動信號幅值γ=2.54，混沌態仿真設置為γ=2.53，為了便于觀察，周期態相圖選取后15 000點繪制如圖3所示。

從圖3中可以看出，經系統過渡過程后，周期態時所產生的狀態變量差值接近為零，混沌態時所產生的狀態變量差值波動較大。

文中提到的方法可以實時檢測，因此可以判斷系統模型是否處于判斷間歇混沌狀態。將驅動信號角頻率ω0=1 rad/s，待測信號角頻率ω1=1.02 rad/s，通過新相態判別法進行實時判別如圖4所示。

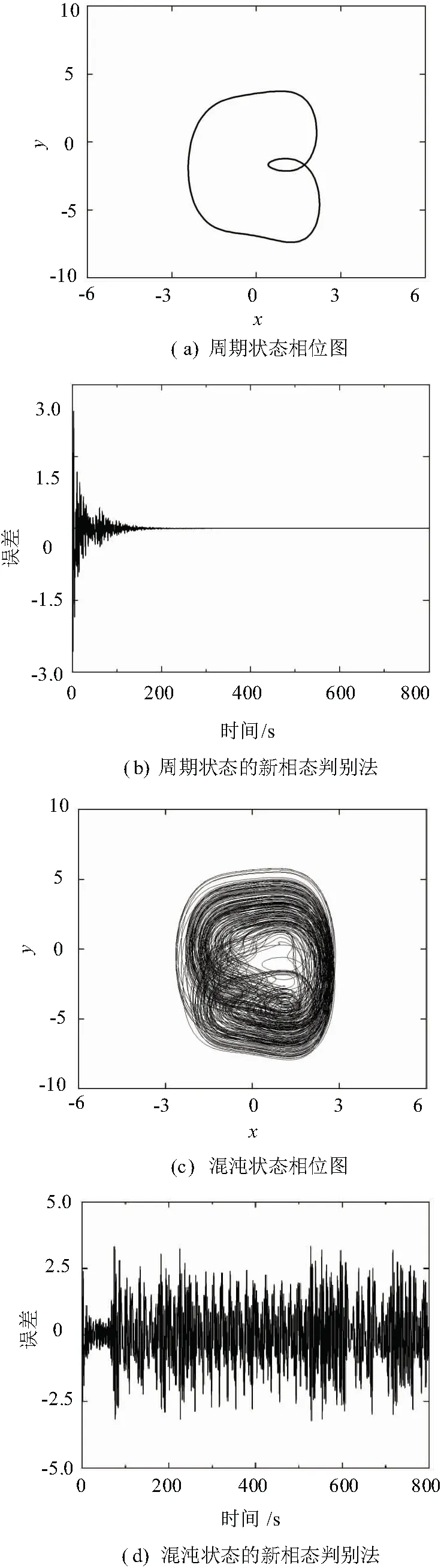
圖3 新型混沌振子相變狀態

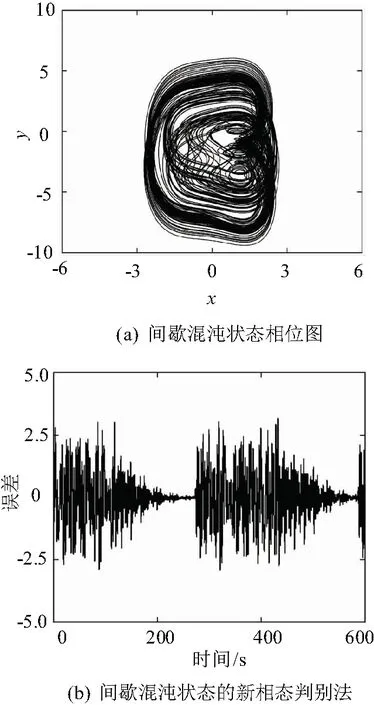
圖4 間歇混沌狀態

通過間歇混沌狀態相位圖，系統模型的運動軌跡顯示出存在部分周期軌道，但整體的運動軌跡表現為混沌狀態。利用新相態判別法，可以清楚看到振子模型由周期態轉變為混沌態的瞬時時刻。由圖4(b)可知，在系統模型運動至271 s時出現了幅值相反頻率不同的信號，運動至585 s時待測信號再次出現，由此可以截取相鄰突變間隔視為間歇混沌周期T=2π/Δω=314 s，進而反推出頻率差Δω=0.02 rad/s，待測信號角頻率ω1=±1.02 rad/s。若再搭配適應步長型間歇混沌狀態法[17]或是振子陣列法[18]能夠對未知頻率信號的計算機或電路實現自動識別。

3 仿真檢測實驗

3.1 不同噪聲背景下的信噪比門限

由于周期激勵的混沌振子具有小頻率參數限制，采用尺度變換[1]，即可檢測任意頻率信號。

(7)

在真實的工作環境下，主要以色噪聲的形式存在，借助四階帶通濾波器將頻域均勻分布的白噪聲來轉化為色噪聲，濾波器的傳遞函數為[19]:

(8)

信噪比(Signal-to-noise Ratio, SNR)定義為系統中所需的有效信號與無規則噪聲信號的比值:

SNR=10lg (PS/Pn)

(9)

式中Ps為信號功率;Pn為噪聲功率。

取驅動信號ω0=1 000 rad/s，高斯白噪聲方差σ2=0.001，仿真時間T=1 s。檢測信噪比門限值如表2所示。

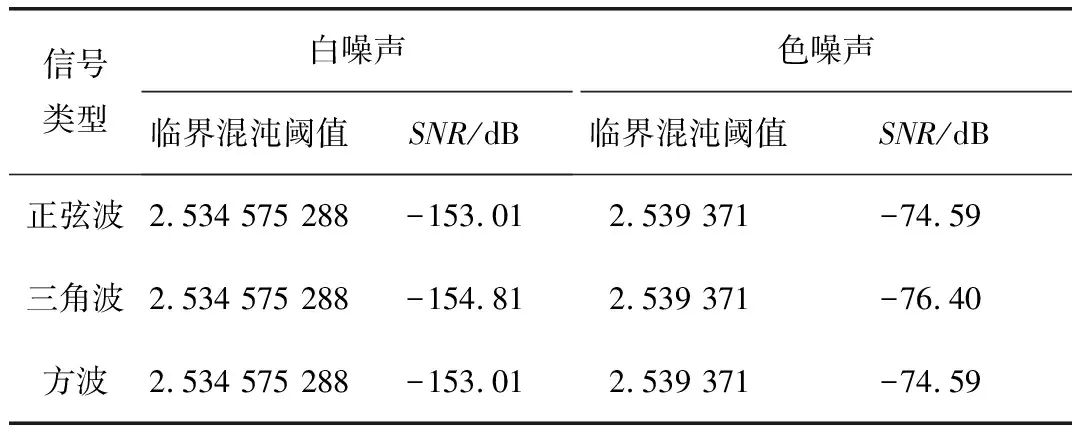
表2 周期信號的信噪比門限檢測結果

由此可知，輸入高斯白噪聲時，臨界混沌閾值2.534 575 288，可以實現幅值10-9V的檢測，所達到的信噪比門限為-153.01 dB；當輸入噪聲為色噪聲時，臨界混沌閾值為2.539 371，可實現幅值為10-6V的檢測，信噪比門限為-74.59 dB。

3.2 新相態判別法的電路仿真

搭建新相態判別法的電路仿真，采用模塊化設計方式，通過積分器電阻電容值的設定可以檢測多種頻率待測信號，為減小相對誤差應選取的合適的運算放大器。此次仿真設置ω0=10 rad/s，系統周期T=0.628 s。

首先根據新相態判別法原理使Y狀態變量經處理后通過減法器和絕對值電路得到間隔整周期的正向差值，其次再利用電壓比較器設定門檻電壓值UTH=0.9 V和四輸入多延時與門結構將其轉化為數字量。當最后表現為高電平時，表明振子模型的運動軌跡為周期運動；當最后表現為低電平時，表明振子模型的運動軌跡為混沌運動；當最后表現為高低電平周期性交替，表明振子模型的運動軌跡為間歇混沌狀態，由此即可利用模擬電路完成自動區分系統模型的運動軌跡，如圖5所示。

3.3 變壓器局部放電檢測

變壓器局部放電信號等效數學模型有四種[20]，分別是單指數衰減、雙指數衰減、單指數衰減振蕩和雙指數衰減振蕩。由于定子線圈的感抗偏大，傳感器采集局部放電的過程中，會易使信號出現衰減振蕩過程，所以此次檢測選取單、雙指數衰減振蕩型的局部放電信號為：

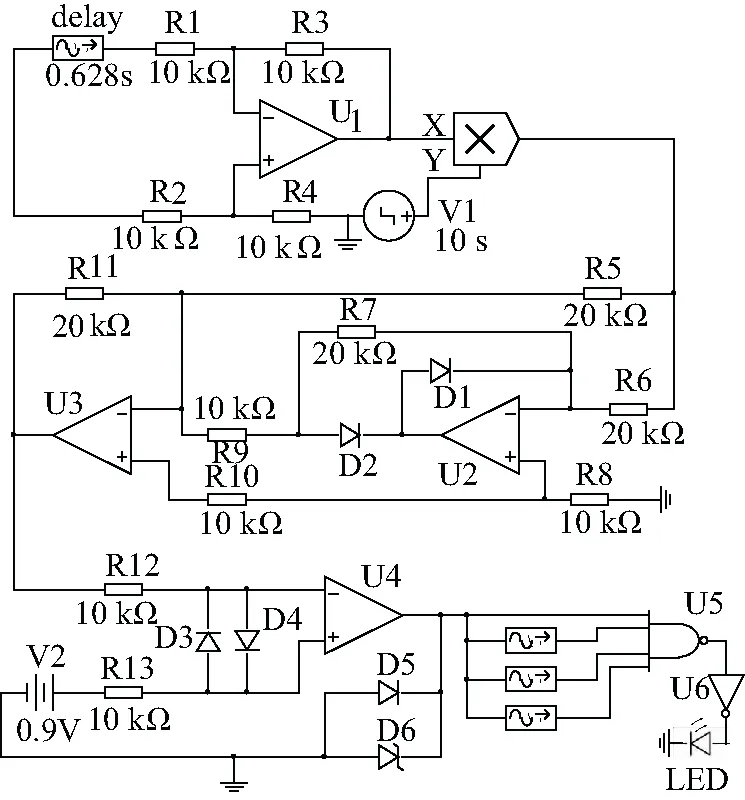
圖5 新相態判別法的仿真電路

(10)

式中A1、A2是信號幅值；α1、α2為衰減系數；θ是初相位。

取信號峰值為1 mV，衰減系數為107，局部放電信號頻率f1=600 MHz，加入方差為σ2=0.01白噪聲，信噪比為-66.02 dB，調節臨界混沌閾值高于信號峰值為104精度差倍數，即γd=2.644 677 86，局部放電信號及噪聲信號如圖6所示。

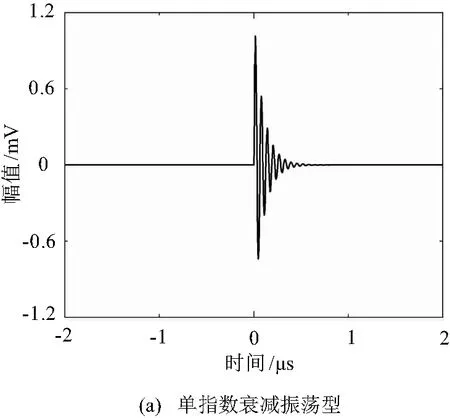
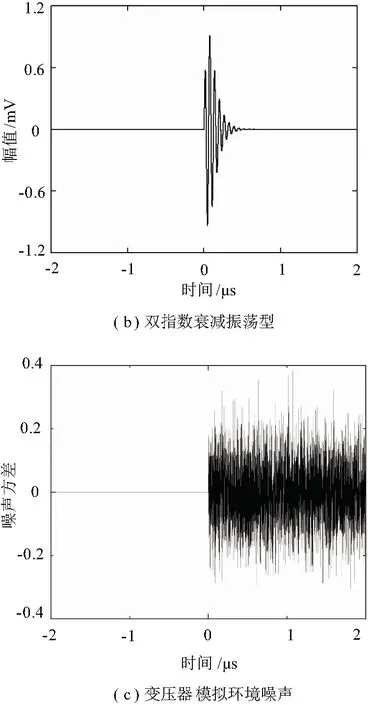
圖6 混沌系統輸入信號

若輸入信號的幅值過低，頻率較高，采用其余方法必須使用放大器和檢波電路，通過對輸入信號逐步放大、降頻[21]。而混沌振子本身對小幅值信號敏感，進行尺度變換能檢測超高頻信號，采用新相態判別法區分混沌振子的運動軌跡從而獲取檢測結果如圖7所示，相位圖取后15 000點繪制。

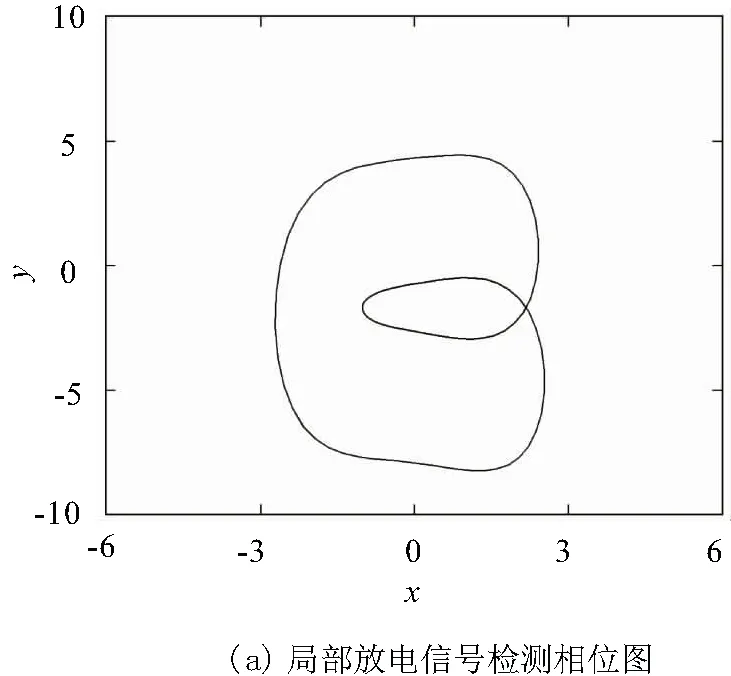
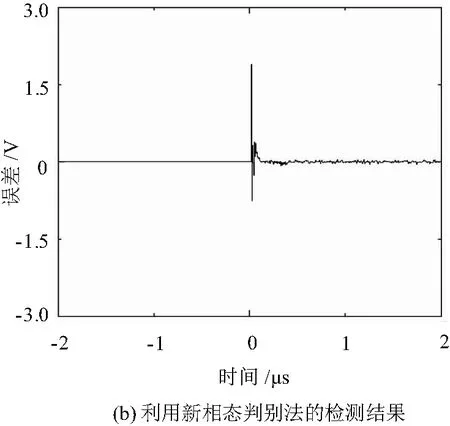
圖7 變壓器局部放電檢測結果

通過變壓器局部放電檢測結果可知，利用白噪聲中混入局部放電信號作為輸入信號，正反相雙混沌系統運動軌跡會出現周期態，并采用所提出的判斷方法可實時輸出檢測結果，圖7(b)中時刻0 s后穩態下的連續小幅度的誤差是由白噪聲的干擾。

4 結束語

文章利用新型混沌振子，可實現信噪比門限為-153.01 dB的檢測。通過提高臨界混沌閾值的精度104倍，能夠僅利用雙振子檢測任意起始相位的待測信號，減少了振子數量。利用系統周期特點，提出新相態判別法，具有普適性，能夠自動判別相變狀態包括間歇混沌狀態，并能實時記錄間歇混沌狀態周期，同時設計新相態判別仿真電路驗證可行性。能實現600 MHz指數衰減振蕩型毫伏級局部放電信號的檢測，由于自身良好的抗噪性，所以混沌振子檢測局部放電信號有著廣闊的前景。