建筑因素對環(huán)境溫度的顯著影響分析

盧躍靜，武新乾，王飛飛

（河南科技大學，河南 洛陽 471023）

引文

隨著我國經(jīng)濟的迅速發(fā)展，建筑業(yè)已成為我國國民經(jīng)濟的重要支柱產(chǎn)業(yè)[1]。近年來，一些學者對建筑因素對環(huán)境溫度的影響進行了研究。耿紅凱等（2020）指出樣地溫度與綠量（含三維綠量、喬木覆蓋率、綠化覆蓋率等指標）存在負相關關系[2]；孫喆（2020）提出城市形態(tài)要素對熱環(huán)境具有顯著影響，建筑密度上升導致地表溫度上升，容積率、綠地率的提升引起地表溫度下降[3]；王琳（2017）指出中庭式建筑中庭各層溫度的特點是沿高度方向，高度越高，溫度越高[4]。

本文主要就建筑因素綠化率、密度和高度對環(huán)境溫度的影響進行顯著性分析。

1 數(shù)據(jù)來源與數(shù)據(jù)處理

1.1 數(shù)據(jù)來源

數(shù)據(jù)來源：河南科技大學建筑學院實地測量數(shù)據(jù)，包括建筑因素綠化率、密度、高度及其對應環(huán)境溫度440組數(shù)據(jù)；建筑因素綠化率、密度、高度與環(huán)境溫度散點圖見圖1-圖3。

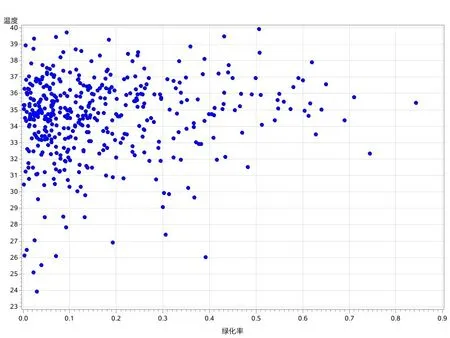
圖1 溫度與綠化率散點圖

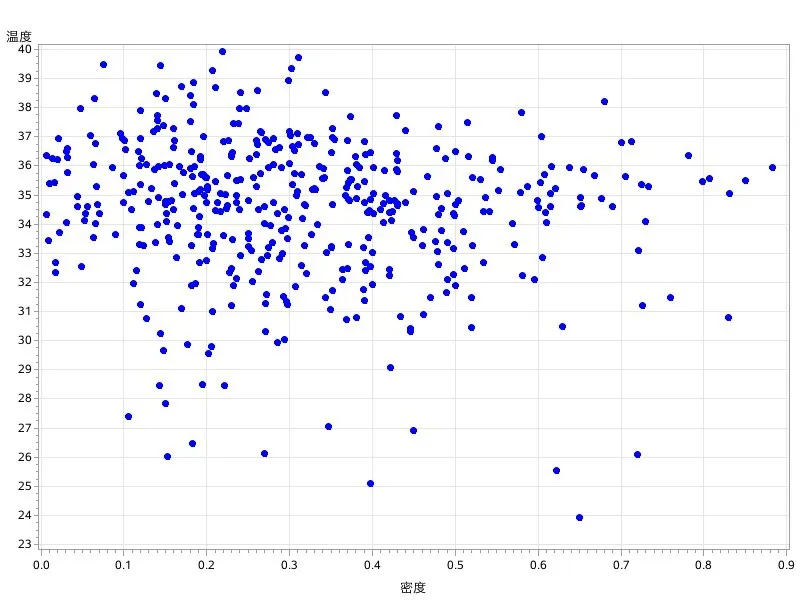
圖2 溫度與密度散點圖

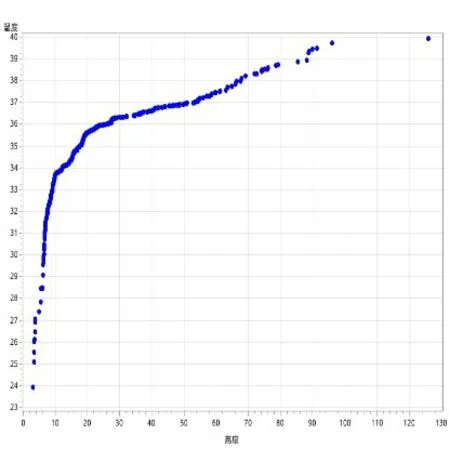
圖3 溫度與高度散點圖

2.2 數(shù)據(jù)處理

數(shù)據(jù)處理：對綠化率、密度、高度數(shù)據(jù)進行Min-max標準化，即：

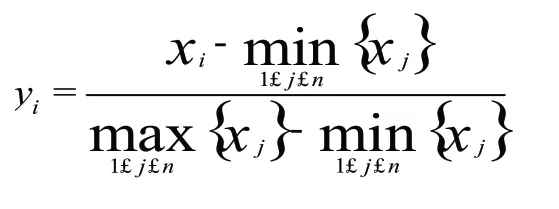
其中yi為xi標準化的值。

2 建筑因素對環(huán)境溫度的影響

將綠化率、密度、高度分為11個水平，每組40個數(shù)據(jù)進行單因素方差分析[5]。

對不同綠化率水平下的溫度進行正態(tài)性檢驗，結果見表1。由表1可知，綠化率水平1、水平2、水平4、水平7 對應溫度不服從正態(tài)分布，則不能對綠化率進行單因素方差分析[6]。

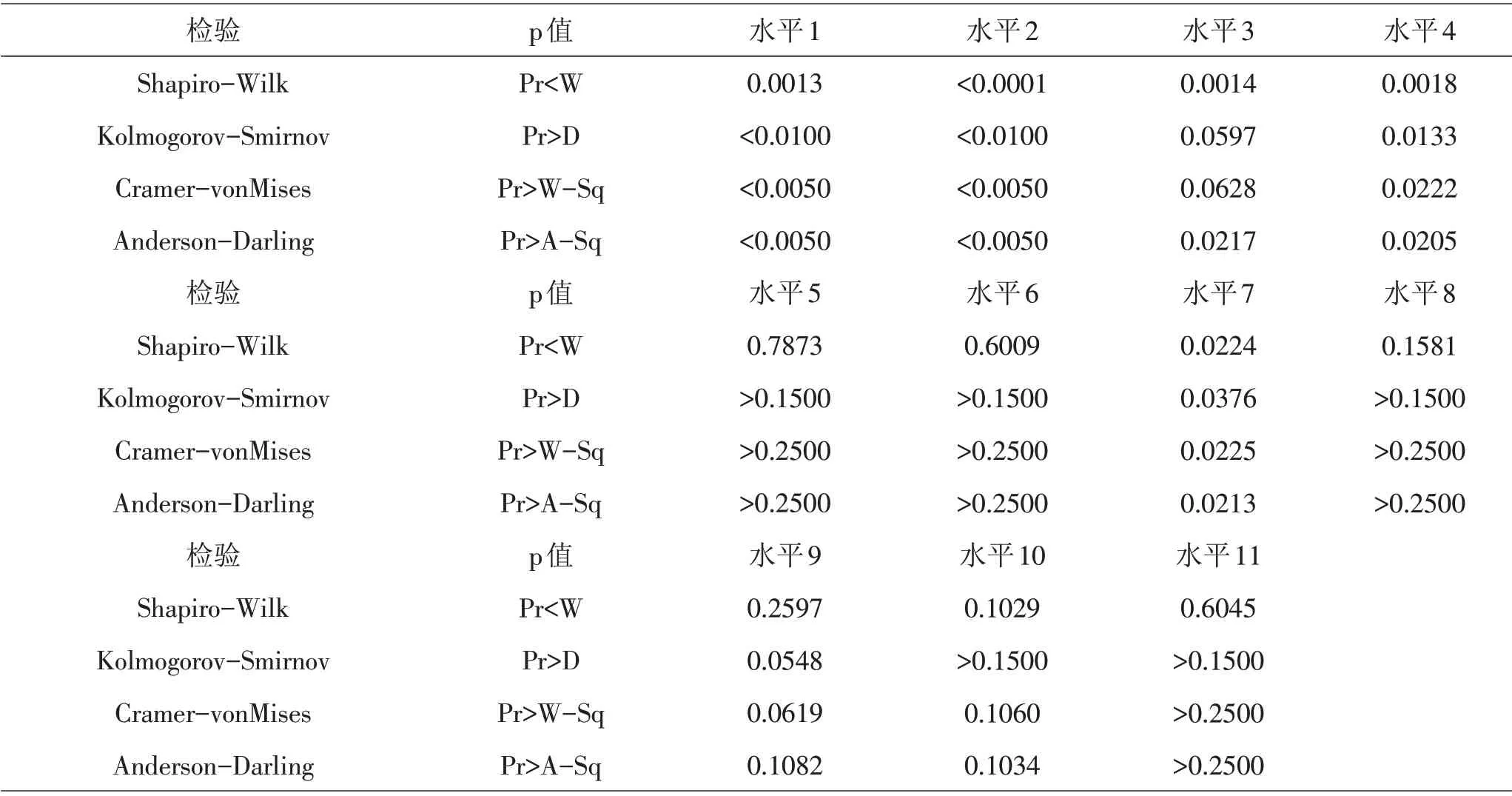
表1 不同綠化率水平下的溫度正態(tài)性檢驗

對不同密度水平下的溫度進行正態(tài)性檢驗，結果見表2。由表2可知，密度水平4、水平8、水平11對應溫度不服從正態(tài)分布，從而不能對密度進行單因素方差分析[6]。

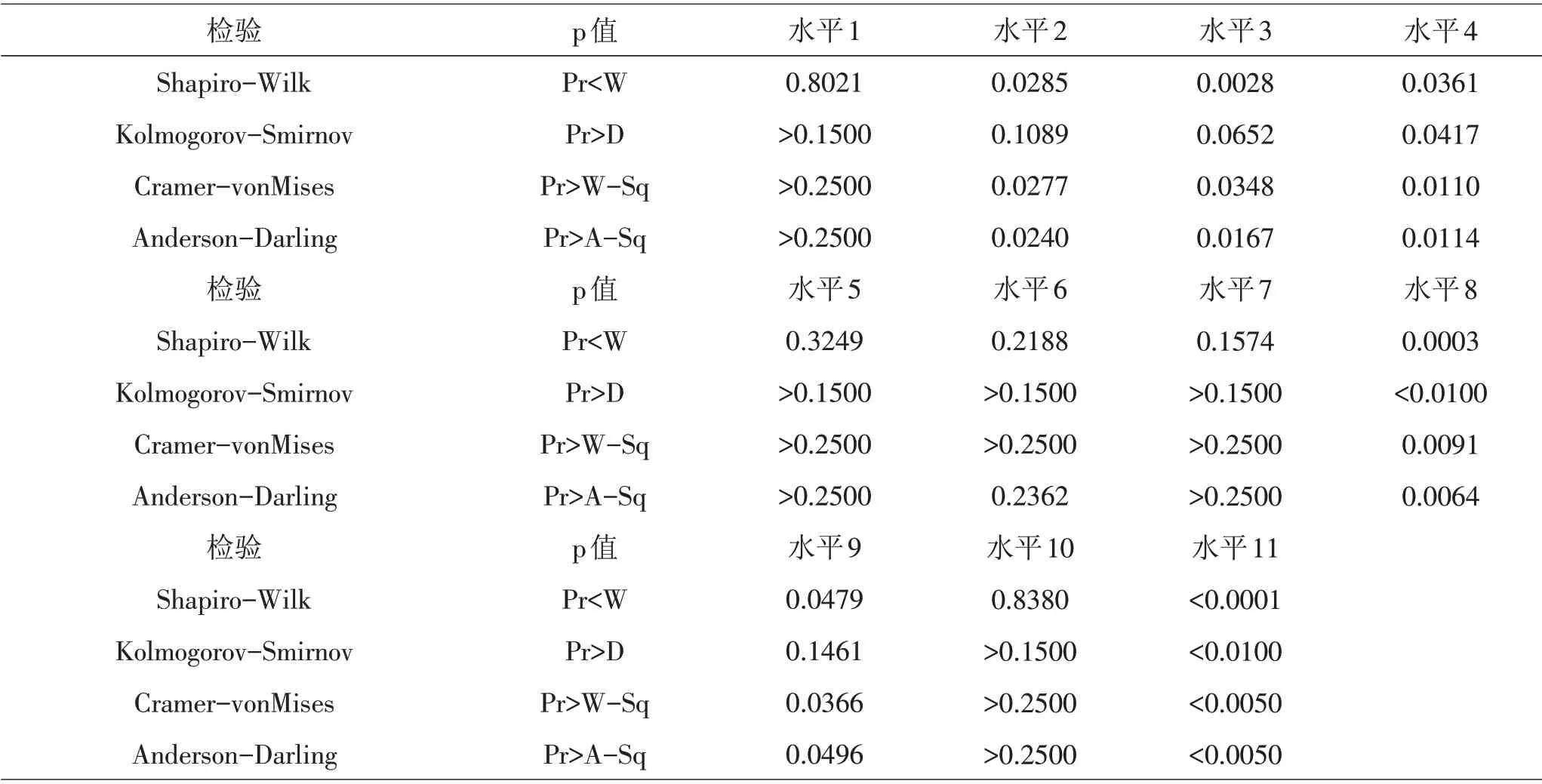
表2 不同密度水平下的溫度正態(tài)性檢驗

對不同高度水平下的溫度進行正態(tài)性檢驗，結果見表3。由表3可知，高度水平1、水平3、水平9 對應溫度不服從正態(tài)分布，不能對高度進行單因素方差分析[6]。

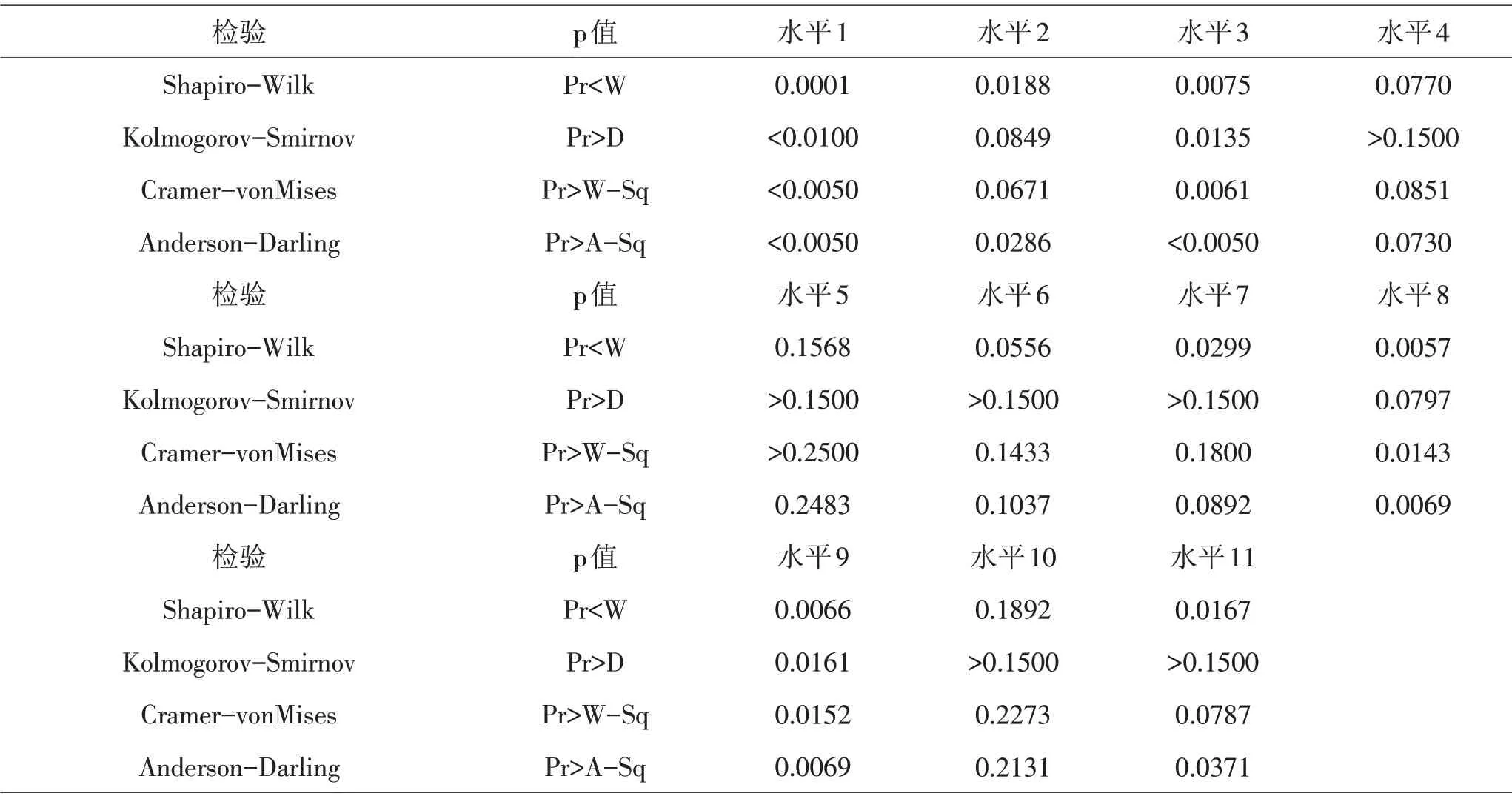
表3 不同高度水平下的溫度正態(tài)性檢驗

對于建筑因素綠化率、密度、高度，均存在水平對應溫度不服從正態(tài)分布，故不能直接對該組數(shù)據(jù)進行方差分析，且考慮到在探究建筑因素對溫度的影響時沒有進行變量控制，于是進行K-means 聚類[7]以達到控制變量的目的，從而更好地探究建筑因素對溫度的影響。

2.1 建筑因素綠化率對環(huán)境溫度的影響

利用建筑因素密度、高度標準化后數(shù)據(jù)，用手肘法畫出肘部圖，見圖4。由圖4，曲線在K=4 時，曲率最大，則最佳類聚數(shù)量值K 值取4。利用R軟件進行K-means 聚類[7]，聚類結果見圖5。

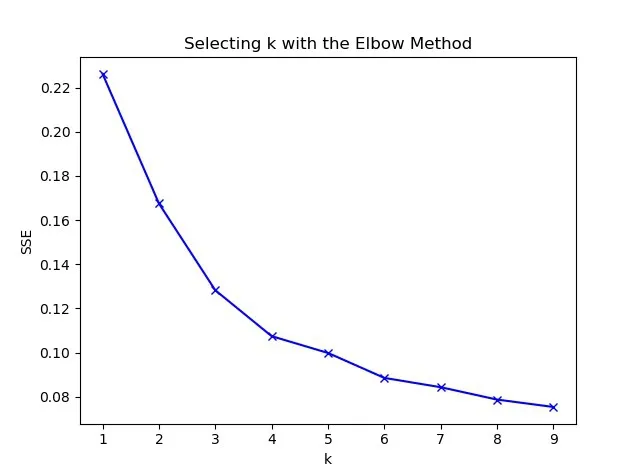
圖4 密度、高度聚類肘部圖

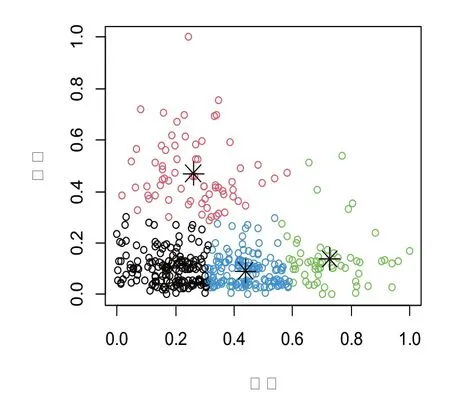
圖5 密度、高度聚類結果圖

根據(jù)密度、高度標準化數(shù)據(jù)進行K-means聚類，將樣本分為4類，數(shù)據(jù)個數(shù)分別為203、154、34、49。選取數(shù)據(jù)個數(shù)為203的類別進行處理，綠化率因素下的8個分類變量分別是0～0.1、0.1～0.2、0.2～0.3、0.3～0.4、0.4～0.5、0.5～0.6、0.6～0.7以及0.7以上總稱為綠化率因素下的八個水平[8]。對每個綠化率水平下的溫度進行正態(tài)性檢驗，結果見表4。由表4可知，綠化率水平1、水平2、水平4、水平5下的溫度數(shù)據(jù)不服從正態(tài)分布；此外，進行Levene方差齊性檢驗，結果見表5。由表5可知，p值＜0.05，方差非齊。故不能采用單因素方差分析方法探究綠化率對環(huán)境溫度的影響[6]。

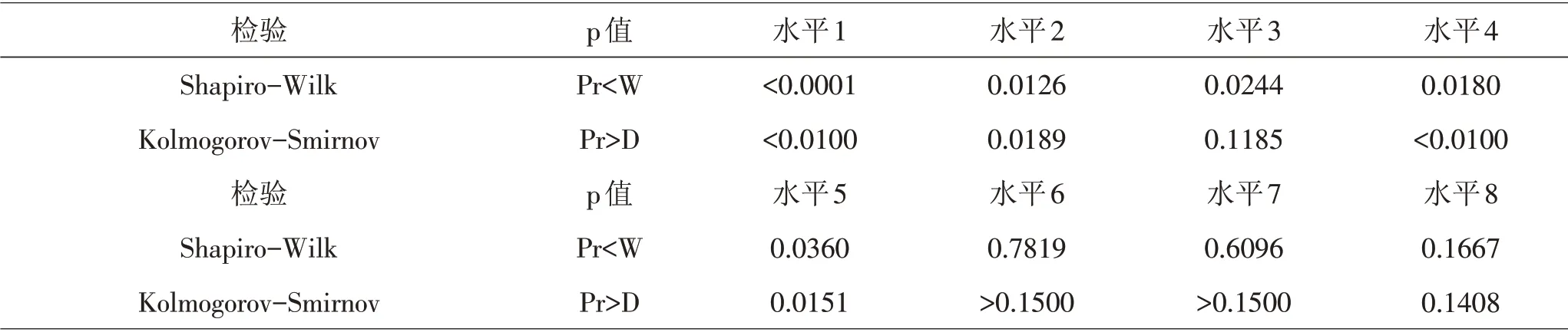
表4 不同綠化率水平下溫度數(shù)據(jù)的正態(tài)檢驗結果

表5 Levene方差齊性檢驗

考慮采用非參數(shù)檢驗方法Kruskal-Wallis方法[9]進行檢驗。對數(shù)據(jù)進行Kruskal-Wallis檢驗，結果[10]見表6。由表6可知，p值＜0.05，拒絕原假設，即認為建筑因素綠化率對環(huán)境溫度有顯著影響。

表6 Kruskal-Wallis檢驗結果

2.2 建筑因素密度對環(huán)境溫度的影響

將數(shù)據(jù)進行標準化，利用建筑因素綠化率、高度標準化數(shù)據(jù)畫出肘部圖，見圖6。由圖6可知，曲線在K=3 時，曲率最大，由此確定最佳類聚數(shù)量值K 值為3，即將原始數(shù)據(jù)聚為3類。利用R 軟件進行K-means 聚類[7]，聚類結果見圖7。

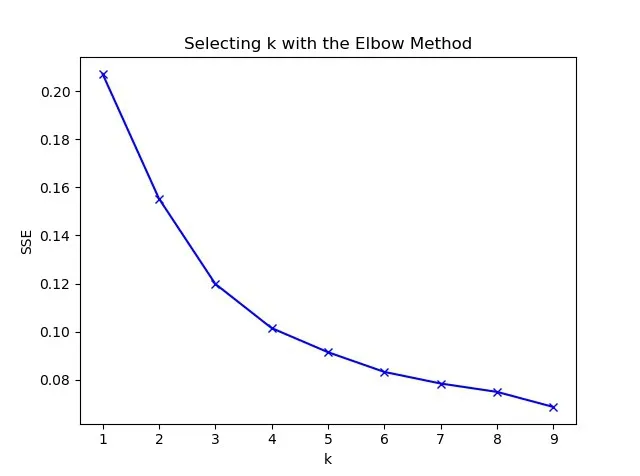
圖6 綠化率、高度聚類肘部圖

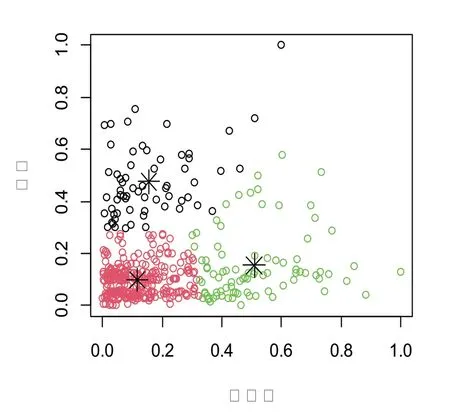
圖7 綠化率、高度聚類結果圖

根據(jù)綠化率、高度標準化數(shù)據(jù)進行Kmeans 聚類，將樣本分為3類，數(shù)據(jù)個數(shù)分別為91、287、62。選取數(shù)據(jù)個數(shù)為287 的類別進行處理，密度因素下的9 個分類變量分別是0～0.1、0.1～0.2、0.2～0.3、0.3～0.4、0.4～0.5、0.5～0.6、0.6～0.7、0.7～0.8 以及0.8～0.9 總稱為密度因素下的九個水平[8]。對每個密度水平下的溫度進行正態(tài)性檢驗，結果見表7。由表7可知，密度水平2、水平4、水平5、水平7、水平9 下的溫度數(shù)據(jù)不服從正態(tài)分布；此外，進行Levene 方差齊性檢驗，結果見表8。由表8可知，p 值＞0.05，不能拒絕原假設，即認為方差齊性。但由于存在密度水平對應溫度正態(tài)性檢驗未通過，故不能采用單因素方差分析方法探究密度對環(huán)境溫度的影響[6]。

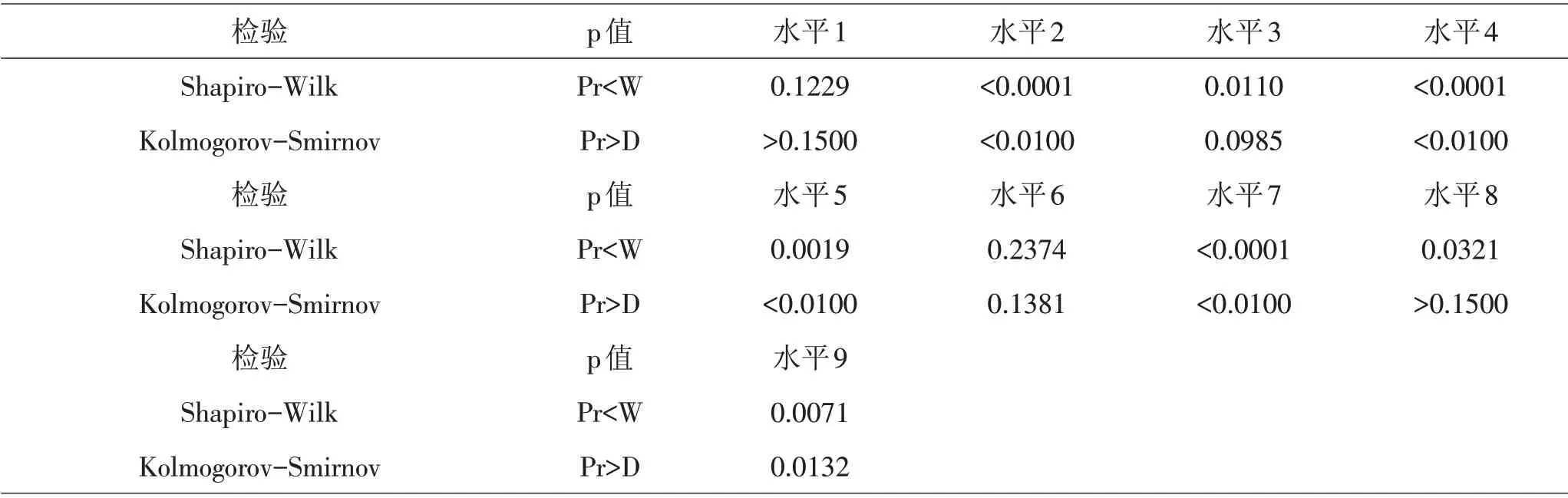
表7 不同密度水平下溫度數(shù)據(jù)的正態(tài)檢驗結果

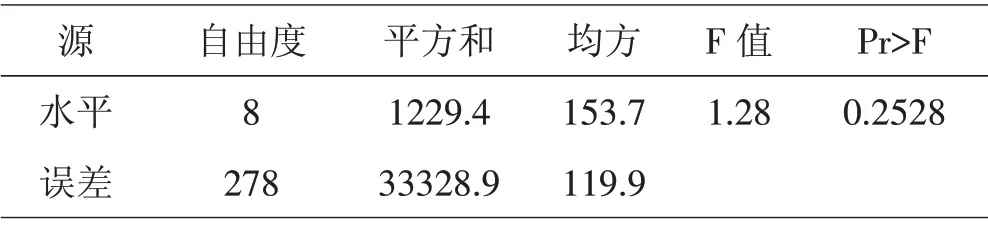
表8 Levene方差齊性檢驗結果

故采用Kruskal-Wallis 檢驗[9]探究建筑因素密度對環(huán)境溫度的影響。檢驗結果見表9。由Kruskal-Wallis 檢驗結果[10]，p 值＞0.05，不能拒絕原假設，即認為建筑因素密度對環(huán)境溫度無顯著影響。

表9 Kruskal-Wallis檢驗結果

2.3 建筑因素高度對環(huán)境溫度的影響

將數(shù)據(jù)進行標準化，利用建筑因素綠化率、密度標準化數(shù)據(jù)畫出肘部圖，見圖8。由圖8可知，曲線在K=5 時，此時誤差平方和SSE 的下降趨于緩慢，由此確定最佳類聚數(shù)量值K 值為5，即將原數(shù)據(jù)分為5類。利用R 軟件進行K-means 聚類[7]，聚類結果見圖9。

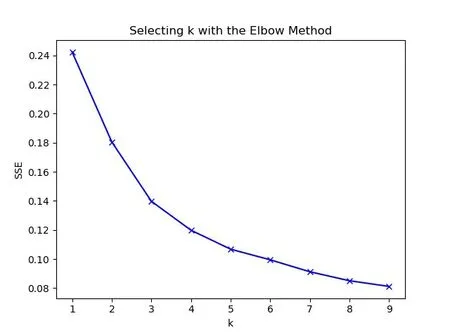
圖8 綠化率、密度聚類肘部圖

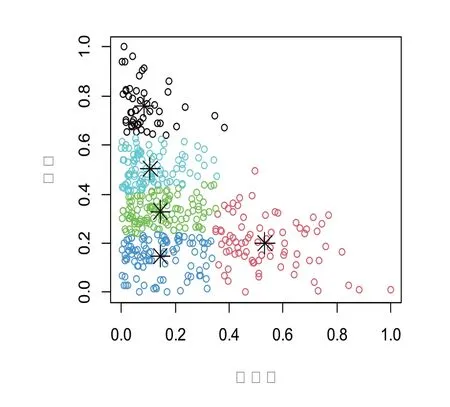
圖9 綠化率、密度聚類結果圖

根據(jù)綠化率、密度標準化數(shù)據(jù)進行Kmeans 聚類，將樣本分為5類，數(shù)據(jù)個數(shù)分別為127、66、69、116、62。選取數(shù)據(jù)個數(shù)為127的類別進行處理，高度因素下的7 個分類變量分別是0～10、10～20、20～30、30～40、40～50、50～60、以及60 以上總稱為高度因素下的七個水平[8]。對每個高度水平下的溫度進行正態(tài)性檢驗，結果見表10。由表10可知，高度水平1下的溫度數(shù)據(jù)不服從正態(tài)分布；此外，進行Levene 方差齊性檢驗，結果見表11。由表11可知，p 值＞0.05，不能拒絕原假設，即認為方差齊性。但由于存在高度水平對應溫度正態(tài)性檢驗未通過，故不能采用單因素方差分析方法探究高度對環(huán)境溫度的影響[6]。

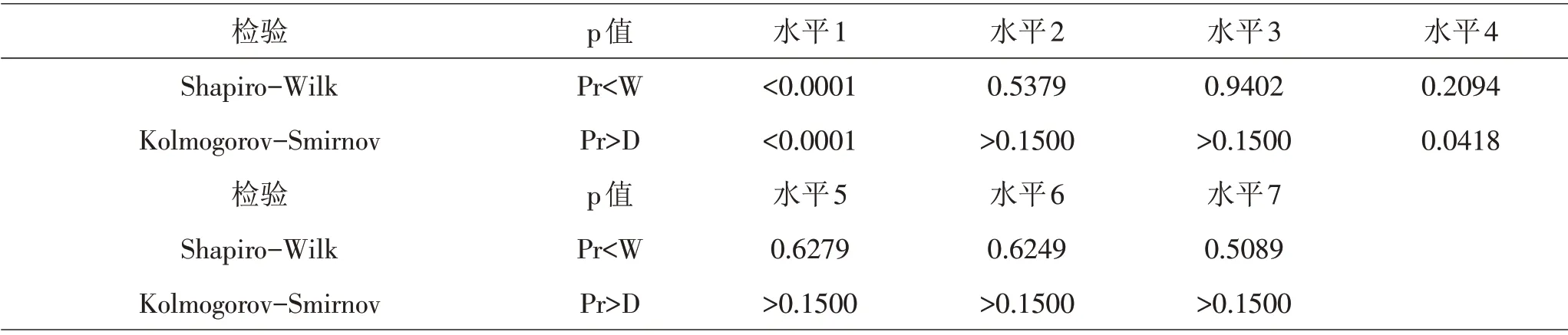
表10 不同高度水平下溫度數(shù)據(jù)的正態(tài)檢驗結果

表11 Levene方差齊性檢驗結果

考慮采用非參數(shù)檢驗方法Kruskal-Wallis方法[9]探究建筑因素高度對環(huán)境溫度的影響。檢驗結果見表12。由Kruskal-Wallis 檢驗結果[10]，p 值＜0.05，拒絕原假設，即認為建筑因素高度對環(huán)境溫度有顯著影響。

表12 Kruskal-Wallis檢驗結果

3 結語

本文就三個建筑因素對環(huán)境溫度的顯著影響進行了探究，通過K-means動態(tài)聚類控制變量，具體檢驗了數(shù)據(jù)是否滿足單因素方差分析的條件，運用非參數(shù)檢驗得出建筑因素綠化率、高度對環(huán)境溫度有顯著影響，建筑因素密度對環(huán)境溫度的影響不顯著的結論。因此，可通過改變建筑因素綠化率、高度以減弱熱島效應，提高環(huán)境質(zhì)量，推進綠色建筑發(fā)展。