基于STEAM理念的高等數學課堂教學模式探究
——以牛頓—萊布尼茨公式為例

王湘萍

（貴州師范大學數學科學學院，貴州貴陽 550001）

1 STEAM教育及特點

STEAM教育源自20世紀80年代美國人提出的STEM教育，是當今國際社會探索21世紀人才培養的一種教育理念與參照。STEAM教育重視數學、科學、技術、工程、藝術等學科的相互融合，突出培養學生的動手能力和跨學科思維能力，建構了文、理、術等多學科融合的完整知識體系。

STEAM教育的主要特點是通過項目問題情境、創新成果導向等核心教學活動，培養學生設計與解決問題能力、溝通和表達能力以及創新應用能力 ，促進學生跨學科思維能力的發展，培養學生的數學核心素養。

2 現行高等數學課堂教學模式存在的問題

目前，大部分高等數學課堂采用的是傳統的教學模式——黑板+PPT課件，利用教育新技術、新教學手段和方法的較少。現行高等數學課堂教學模式主要存在以下幾個問題：

（1）近年來，由于高等教育的不斷改革，招生規模不斷擴大，高考時的錄取分數為總體分數，這使得同一專業的學生數學基礎參差不齊，再加上高等數學是公共必修基礎課，相對于高中數學來說，高等數學概念多、抽象，部分學生在學習過程中積極性不高。

（2）課堂教學模式單一，學生聽課狀態不佳，學習參與度不高。

（3）教材內容相對陳舊，教學體系單一，學生的學習興趣不高 。再加上教學計劃和大綱過于陳舊，無法有效幫助學生掌握數學思想、數學方法和學習新知識。

（4）大班教學影響教學效果。大部分班級人數過多，少則七八十人，多則上百人。教師在上課時不能兼顧所有學生，項目化教學、案例教學、翻轉課堂等教學模式開展不起來。

（5）教學手段單一，缺乏現代教育技術的有效整合。其一，所用教室雖裝有多媒體，但只可以使用教學課件，不可上網，沒能真正實現網絡化、信息化；其二，部分教師使用現代教育技術的能力有所欠缺，即使使用現代教育技術進行教學，也僅是把它代替黑板，沒有讓現代教育技術在高等數學教學中真正發揮作用。

3 基于STEAM理念的高等數學課堂教學路徑設計

課堂教學是教師傳授知識的主要陣地，是培養學生能力的重要方式。高等數學課堂教學要注重調動學生學習興趣，培養學生創新能力，全面提高高等數學的教學質量。為此，基于對STEAM教育理念的初步探討，結合當前高校高等數學課堂教學的現狀，以牛頓—萊布尼茨公式為例，設計出高等數學課堂教學新路徑。

3.1 創設有效情境，提出問題，激發學生學習興趣

在教授牛頓—萊布尼茨公式時，可這樣創設有效情境：由定積分定義求時要經過分割、近似、求和、取極限四個步驟，計算過程冗長而繁雜。可先提出問題：能不能找到一種有效、直接的工具來計算定積分？牛頓—萊布尼茨公式就是這樣一種工具。學生在高中已經初步接觸過這個公式，但只是會用，而不知道是怎樣得出來的，為什么要以兩個數學家的名字來命名，通過設問將定積分計算與歷史上著名的科學家等聯系起來，激發學生的求知欲。

3.2 重點講授，喚起記憶，增加知識的關聯

通過對主要知識點的講解來喚醒學生記憶中已有的知識，并與所學知識聯系起來，形成跨學科思維。在講解牛頓—萊布尼茨公式時，重點講授公式的證明過程，讓學生理解積分上限函數的性質和原函數存在定理，把求一個連續函數在區間上的定積分的值與找這個連續函數的一個原函數聯系起來，并了解微積分基本定理是聯系積分學與微分學之間的橋梁。

3.3 基于項目驅動、案例分析，提高主動性

通過對具體案例進行分析，引導學生進行交流探討，鼓勵學生在探索中應用過程性技能，如觀察、提問和討論等，建立起學科之間的聯系，去思考解決實際問題。例如，對牛頓—萊布尼茨公式的證明探討完后，可以安排三個例題。例題的安排遵循由簡到難、從單一到綜合的規律，鼓勵學生根據題目本身特點動手畫出平面圖形，在解題上以問答和分組討論的形式進行。例1較為簡單，利用定積分的性質即可。

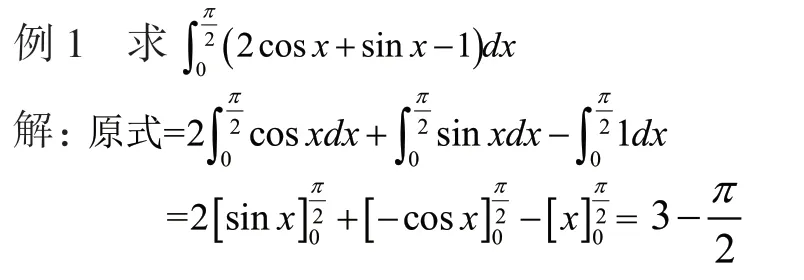
例2、例3都是求分段函數的定積分，這是一個難點。由于牛頓—萊布尼茨公式的前提是被積函數是連續函數，如果不是連續函數或有有限個間斷點，該怎樣求得？引導學生分析，發現在各個積分區間，被積函數都是連續函數，可以利用定積分對積分區間具有可加性的性質求得。將原式中積分區間[0,2]分成兩個積分區間[0，1]，[1，2],求出定積分的值，再相加即可。于是，對分段函數求定積分，可以分段積分，再相加。

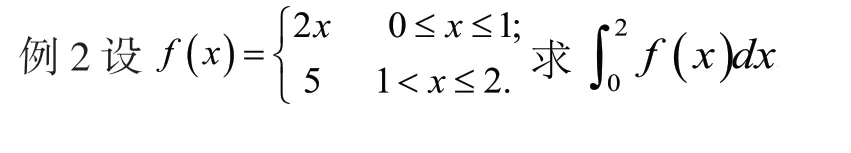
解：∵函數在[0，2]上不連續，但是分段連續

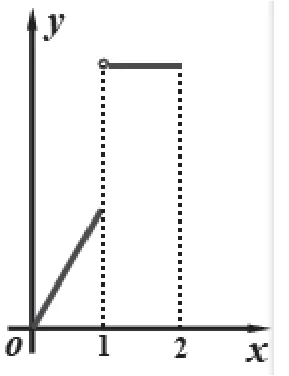
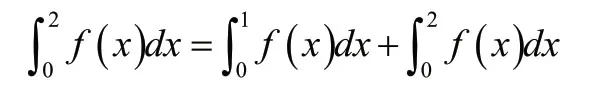
在[1,2]上規定當x=1時，f(x)=5，

解：由圖形可知

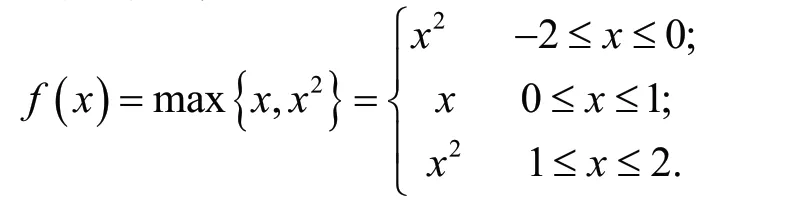
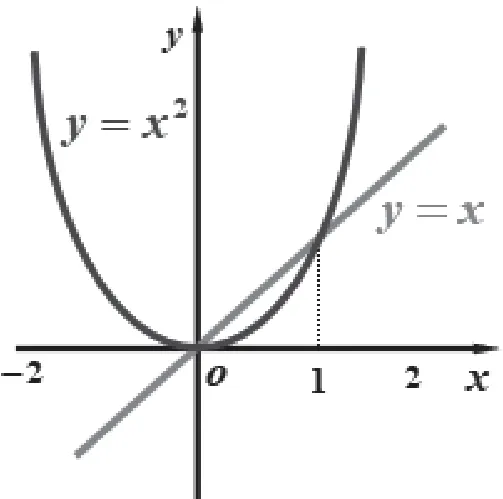
則，原式=

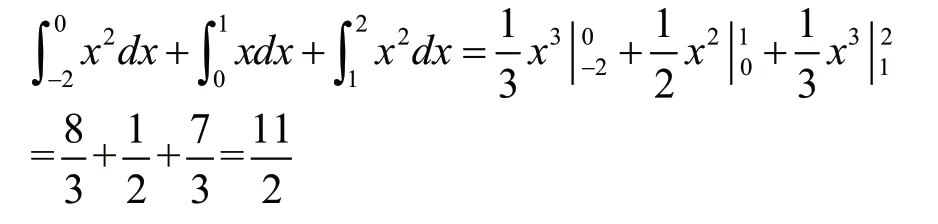
3.4 教學反思，提煉升華

課堂教學最后由教師和學生對整個教學過程和教學結果講行評價反思，推進課程教學近一步提升。在對牛頓—萊布尼茨公式證明結束時進行升華反思[7]，引導學生思考證明中用到了什么定理？哪些知識點？找到微分與積分之間的關系，總結出微積分基本定理不僅是溝通微分學和積分學之間的橋梁，而且還充分體現了數學之美——對稱美（見圖1）。

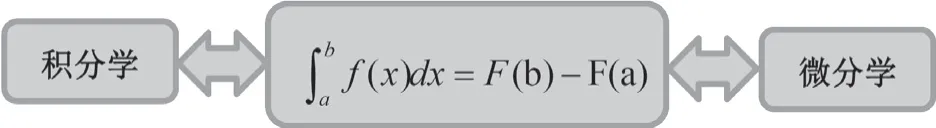
圖1 數學之美——對稱美

4 基于STEAM理念的高等數學課堂教學路徑實施策略

（1）深挖課程思政。將數學歷史、數學概念、數學故事以及數學知識點在現實中的應用作為切入點 ，深挖課程思政，促使STEAM理念在高等數學課堂落地生根。在講授教學牛頓—萊布尼茨公式之前，由歷史故事：17世紀數學史上著名公案“牛頓與萊布尼茨微積分創始人之爭”引入新課，介紹牛頓、萊布尼茨兩位數學家對微積分創始的貢獻，引導學生不僅領略數學文化遺產的魅力，擴展知識領域，又提升人文素養。

（2）注重多學科的交叉融合。STEAM教育最突出的特點就是跨學科性。教師教學設計應注意課程橫向和縱向的融合 ，建立起多學科之間的聯系，培養學生的跨學科、跨區域思維能力。

講授牛頓—萊布尼茨公式的應用時，強調它不僅可以求多個函數的和與差在區間[a,b]上的定積分的值，如例1，還可以用來求曲線弧的長度、曲線圍成的平面圖形的面積和立體的體積等橫向問題，同時在變力做功、水壓力、引力等縱向問題的應用也較為廣泛。

例4 一物體按規律x=ct3做直線運動，介質的阻力與速度的平方成正比。計算物體由x=0移到x=a時，克服介質阻力所做的功[10]。

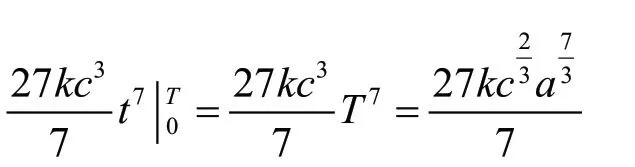
（3）使用多樣化的教學手段。隨著“互聯網+”“大數據”時代的到來，高等數學課堂教學的方法、手段也要隨之改變。

在新課引入時，可以應用動畫制作技術，將牛頓、萊布尼茨的畫像展示給學生；在知識回顧和講解公式的應用時，可以把傳統教學手段與現代化教學手段相結合，即板書與多媒體課件相結合，激發學生學習的興趣，創新課堂教學模式，提升課堂教學效果。

（4）采用案例、項目驅動教學。以問題為驅動的教學模式是STEAM教育最常用的教學模式。課堂上采用案例分析或項目驅動的方式，圍繞一個具體問題進行分析，找到解決問題的方法，踐行“以學生為中心”的理念。

例如，探究牛頓—萊布尼茨公式的證明過程。

定理：如果函數F(x)是連續函數f(x)在區間[a，b]上的一個原函數，那么dx=F(b)-F(a)[12]。

首先對公式進行分析，在精確掌握公式內涵的基礎上，找出已知條件，即F(x)是f(x)的一個原函數，這顯然是不夠的，怎么辦？能否從學過的定理和性質中找到第二個條件？引導學生記憶積分上限的函數和原函數的存在定理，即，連續函數在定義區間內必有原函數存在，而且原函數的形式以積分上限函數Φ(x)=的形式給出，這樣就找到了連續函數f(x)的兩個原函數：F(x)、Φ(x)=，由原函數的定義知道，這兩個原函數之間相差一個常數C，即F(x)-Φ(x)=C(a≤x≤b)，就找到了證明的突破口。

（5）轉變教育觀念，提高教學水平。隨著大數據、“互聯網+”的飛速發展，迫切需要提高教師教學水平。高校教師不但在教學方法、手段上不斷創新，而且在教學模式、教學理念上要進行創新和轉變，打造“金課”，淘汰“水課” ，提升教學質量。在高等數學課堂上引入STEAM教育理念，教師要根據數學學科與信息、工程、技術、藝術等科目各自的特點，尋求它們之間可以融合的突破口，同時關注本學科的前沿知識，及時更新自己的相關知識，進一步提高課堂教學質量，培養學生的數學核心素養[13]。

5 結語

STEAM教育作為一種新興的教育理念，要想在高等數學課堂教學中落地生根，需社會、學校、教師和學生相互配合、共同努力。既要以學生為中心，注重學生的全面發展，又要轉變觀念，改革教學方法和手段，提高教學質量[14]。