不同本構模型對近接施工力學響應的影響研究

馬玉巖，閆飛躍，程麗娟

（1.中國電建集團成都勘測設計研究院有限公司，四川 成都 611130；2.西南交通大學，四川 成都 610031）

0 前 言

巖土體的本構模型反映了巖土體的力學特性，包括應力、應變、強度和時間4者之間的關系。巖土體的本構模型總體可劃分為彈性模型、彈塑性模型、黏-彈塑性模型以及損傷模型等幾個大類。目前，已經有許多種描述巖土體力學特性的本構關系，其中工程中應用比較廣泛的土體模型有：Mohr—Coulomb模型、Cysoil模型、K-G彈性模型、E-B模型、鄧肯E-ν模型等彈性模型和彈塑性模型［1～4］。

近接施工在城市地鐵修建中是不可避免，數值模擬是解決工程問題重要手段之一，合理地選擇巖土體的本構模型是獲得合理數值分析成果的前提。國內外學者依托工程實踐，對本構模型在基坑工程數值模擬的影響以及基坑工程近接既有建（構）筑物的施工開展了大量的研究。秦會來等（2012）［5］對比分析修正劍橋模型和Mohr-Coulomb模型的基坑開挖二維數值模擬結果，認為Mohr-Coulomb模型不能反映加卸載模量差異和土體壓硬性，故不適用于基坑開挖引起的變形模擬；蔣進等（2020）［6］對比分析修正劍橋模型、Mohr-Coulomb模型與Drucker-Prager模型的基坑開挖三維數值模擬結果，發現Mohr-Coulomb模型與Drucker-Prager模型的基坑側壁地表邊緣在開挖后出現隆起變形；馬琳（2018）［7］以昆明某基坑工程近接地鐵1號線施工為背景，研究了基坑開挖對車站及基坑本身的變形影響；楊儉（2018）［8］以珠海某鄰近車站結構的深基坑工程為依托，研究了基坑工程施工對鄰近車站結構及其周圍土體的影響規律。但是在本構模型對深基坑工程近接既有地鐵車站結構施工方面的力學響應影響方面研究很少。

本文以成都地區的一緊鄰地鐵車站的大型基坑工程為例，利用FLAC3D開展近接施工力學響應的研究，通過巖土體變形、地鐵結構變形及受力特征的對比分析，研究不同本構模型的異同和適用性，為類似近接工程提供參考。

1 工程概況

成都市錦城廣場站是成都軌道交通18、16、29號線三線換乘站，三站兩兩相交，呈三角形布置。18號線為南北走向，錦城廣場站為地下四層島式車站，場坪標高491.5m，底板埋深32.4～34.2m，外包總長為367.458m，標準段寬21.7m。16號線位于18號線東側，為西南—東北走向，16號線錦城廣場站為地下三層島式車站，場坪標高491.5m，底板埋深24.3～24.5m，總長為306m，標準段寬20.7m，基坑支護采用直徑1.2m，間距1.8m的排樁結構，插入中等風化泥巖內4m。29號線位于18號線東側、16號線北側，為西北—東南走向，站臺層位于地下五層，底板埋深約41m。三條地鐵線車站圍成的三角形區域為地鐵換乘大廳，底板埋深約為24～24.5m。錦城廣場站及地鐵大廳均采用框架結構體系，其中18號線主體結構（含與16號線、29號線換乘節點）已施工完成，本項目為實施緊鄰18號線主體結構的三角換乘區及16號線。

本項目的平面與剖面位置關系分布如圖1～2所示。

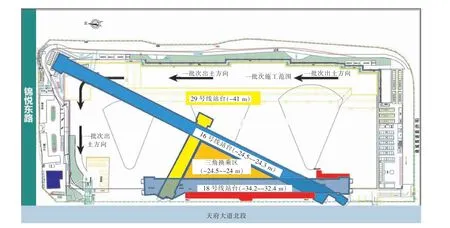
圖1 項目平面示意

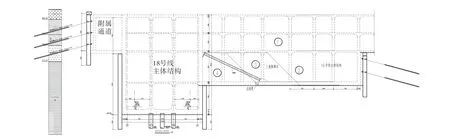
圖2 項目剖面示意

2 本構模型介紹

2.1 Mohr-Coulomb模型

Mohr-Coulomb模型是工程中運用最廣泛的一種本構模型，對于剪切破壞包絡線上的應力點服從非關聯流動法則，而拉伸破壞為關聯流動法則，模型破壞包絡線包含剪切屈服函數及拉伸屈服函數，模型破壞準則見圖3。

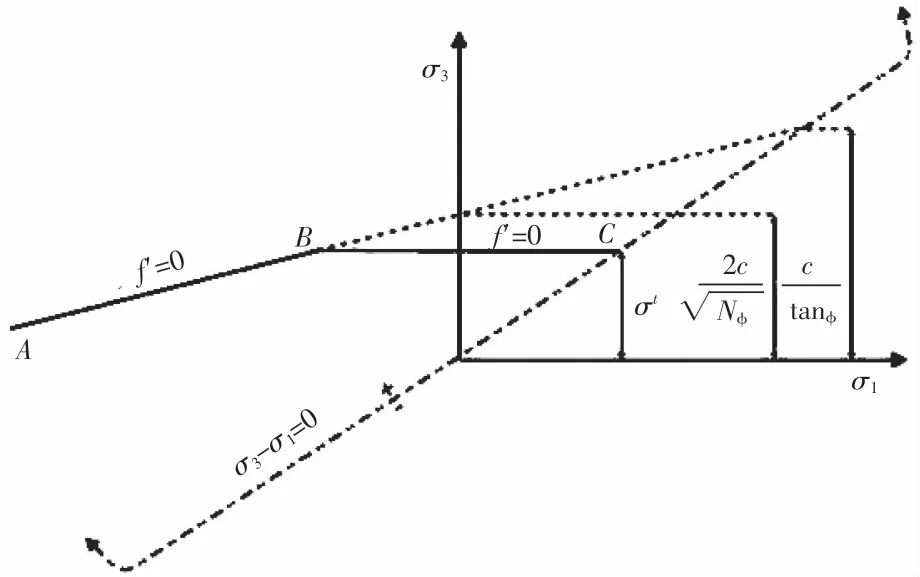
圖3 摩爾庫倫破壞準則

對于剪切破壞準則fs=0，通過A點到B點的直線方程見式（1）：

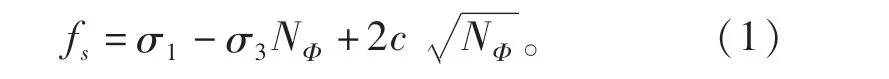
對于拉伸破壞準ft=0，通過B點到C點的直線方程見式（2）：

式中：Φ為摩擦角，c為黏結力，σt為拉伸強度，NΦ=

材料的拉伸強度不能超過fs=0與σ1=σ3相交點的σ3值。

2.2 Cysoil模型

巖土體的塑性變形在微觀上表現為顆粒重分布及顆粒破裂。針對土的力學行為，雙屈服面模型考慮了剪切和體積硬化／軟化，此模型最大的特點是可以通過自定義硬化／軟化曲線，通過在平均應力軸上戴“帽蓋”的方法來移動封閉屈服面來考慮主應力增加引起的塑性變形。在雙屈服面模型中，在應力空間中這個“帽蓋”的形狀為平面，其法向為平均應力主軸方向。但是通過單軸壓縮試驗已經證實，這個“帽蓋”的形狀對側壓力系數的影響很大。Cysoil模型修正了雙屈服面模型，將“帽蓋”的形狀改進為橢圓。模型服從體積準則和流動準則：

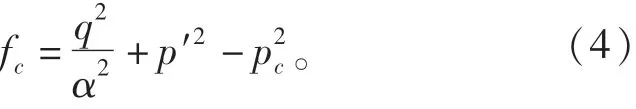
式中：p′為平均有效應力，pc為帽子壓力，α為無量綱常數，用于定義橢圓帽子屈服面。其p′與體積應變e關系曲線如圖4所示。圖4中Ke為彈性模量；H為硬化模量；R=Ke／H為常數。

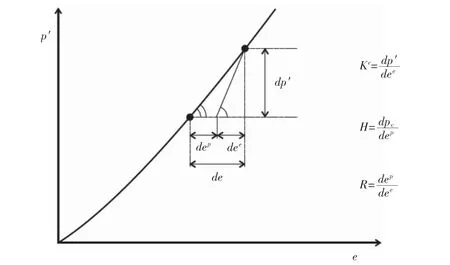
圖4 等向壓縮試驗p′與e關系曲線

3 計算模型與參數

3.1 計算模型

開挖三角換乘區及新建16號線近接既有18號線的三維計算模型如圖5所示，模型邊界范圍取3～5倍基坑開挖深度，影響深度取開挖深度的2～4倍，計算模型側向加水平約束，底部加固定約束，頂面為自由面。模型中巖土體、三角換乘區、地鐵車站及附屬結構為三維實體單元，圍護樁和抗拔樁采用樁結構單元，預應力錨索采用錨索單元。其中結構單元采用彈性模型，而對巖土體分別采用Mohr-Coulomb理想彈塑性模型和Cysoil模型進行研究。

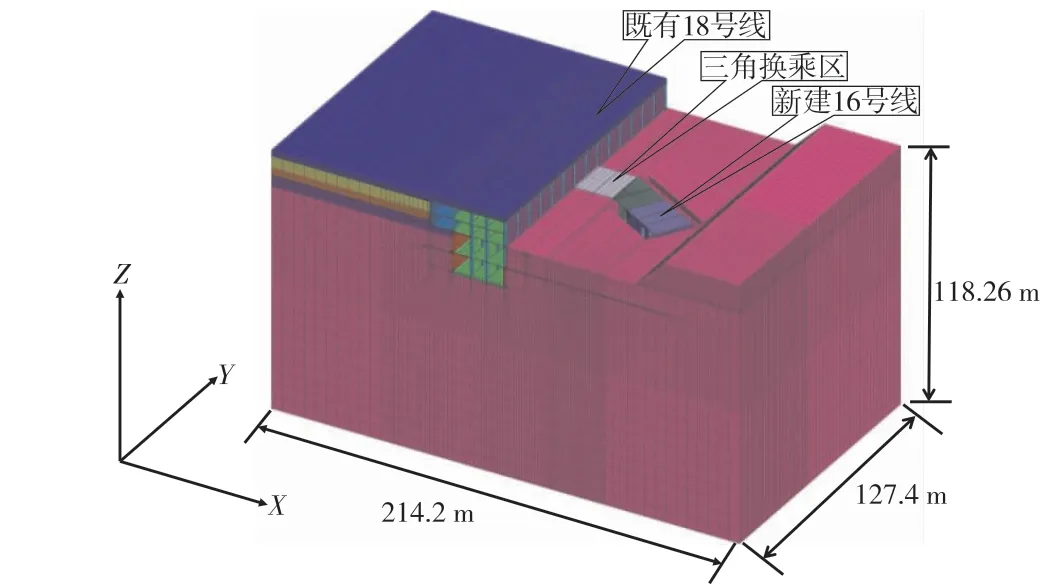
圖5 三維計算模型

3.2 計算參數

工程場地從上到下分布的地層依次是：①雜填土；②黏土；③粉土；④卵石土；⑤中風化泥巖。各地層Mohr-Coulomb模型的物理力學參數依據勘察報告中給出的地層物理力學參數建議值選取如表1，通過數值、室內三軸試驗及現場壓剪試驗確定Cysoil模型的物理力學參數如表2所示，結構的物理力學參數按規范取值。

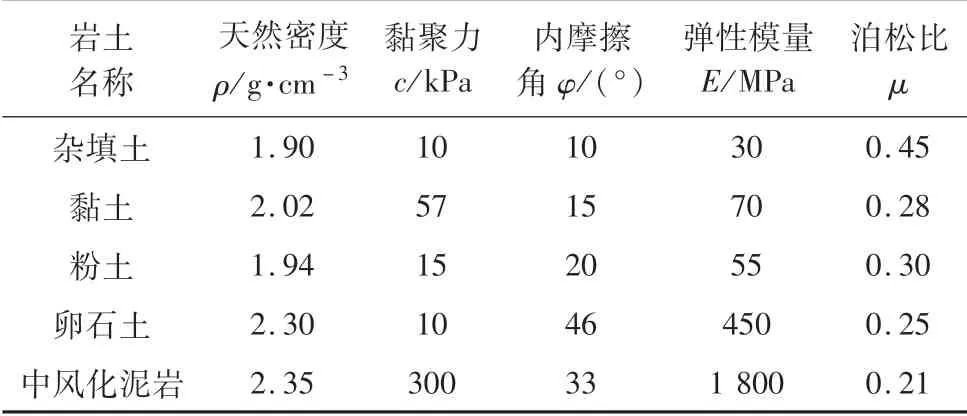
表1 Mohr-Coulomb模型材料參數

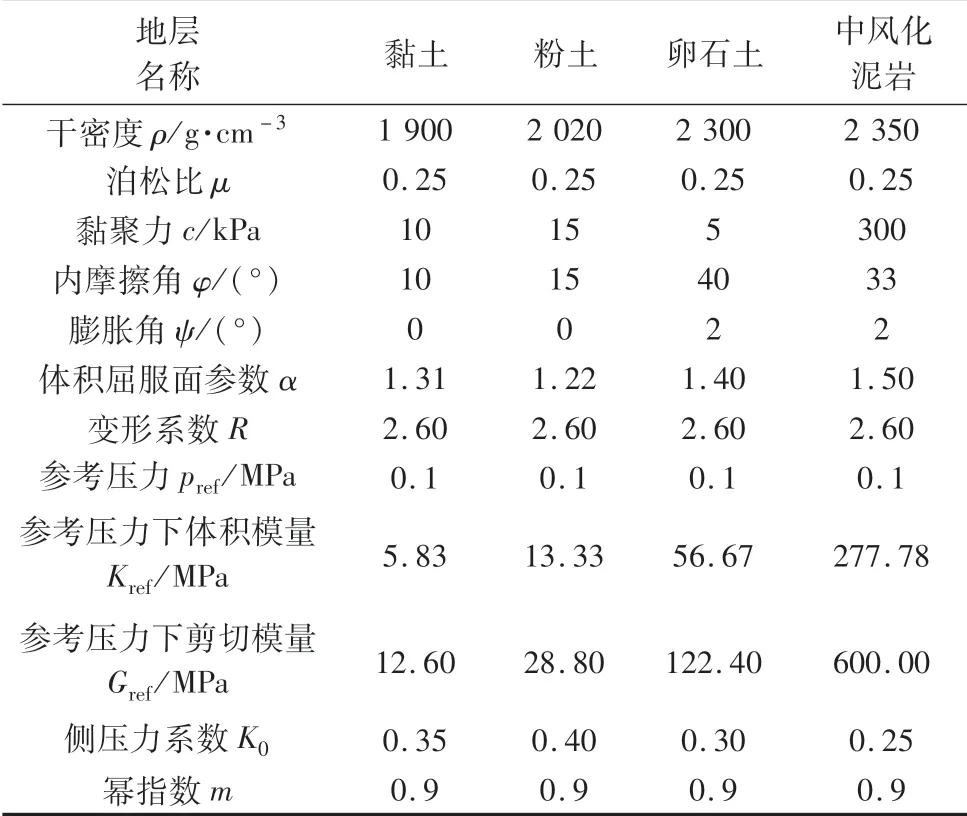
表2 Cysoil模型材料參數

4 近接施工力學響應影響分析

4.1 對巖土體及結構變形特征的影響分析

4.1.1 開挖至地下兩層底板標高

對既有車站結構兩側的土體同步進行分層開挖，Mohr-Coulomb模型（以下簡稱M-C模型）與Cysoil模型（以下簡稱C-Y模型）下開挖完成后的豎向位移和水平位移云圖如圖6～7所示。

由圖6豎向位移云圖可以看出，基坑的開挖引起了既有車站結構兩側和底部土體不同程度的卸荷回彈，由于東側基坑的開挖面積較大，使得東側基坑的回彈大于西側基坑；在西側基坑地表變形方面，M-C模型為隆起，C-Y模型為沉降，且M-C模型的影響范圍較C-Y模型大。由圖7水平位移云圖可以看出，西側基坑側壁變形方面，C-Y模型的水平位移比M-C模型大。

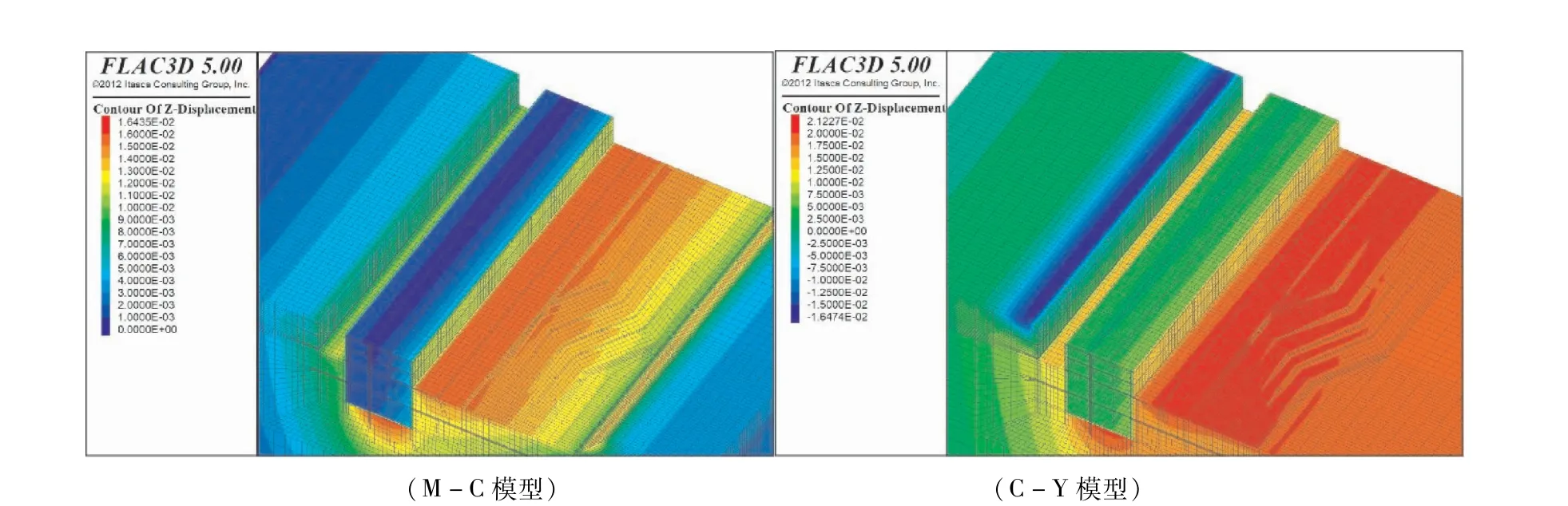
圖6 開挖至地下兩層底板標高豎向位移云圖

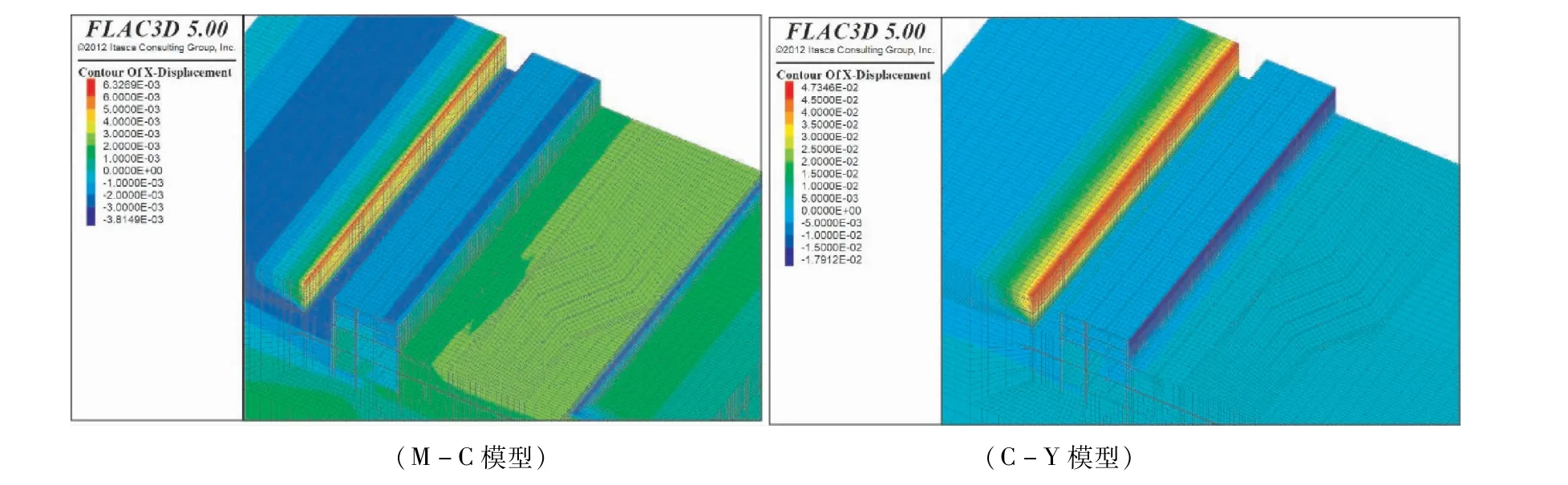
圖7 開挖至地下兩層底板標高水平位移云圖

4.1 .2 施工逆筑部分底板和上部結構

施工完逆筑部分底板和上部結構模型的豎向位移和水平位移云圖，如圖8所示，由豎向位移可以看出，被開挖的部分，坑底出現了卸荷回彈，導致逆筑的結構和既有車站結構出現了向上的位移，隨著與開挖土體距離的增大，既有車站結構底部巖土體的回彈逐漸減小，既有車站結構的變形也在逐漸減小，之后上部結構的施作對基坑底部土體進行了再壓縮，M-C模型與C-Y模型下基坑底部土體再壓縮的變形規律及帶來的結構變形規律相似。

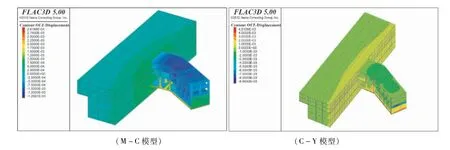
圖8 施工逆筑部分底板和上部結構豎向位移云圖

4.2 對既有車站結構的變形影響分析

為了能更直觀地研究M-C模型與C-Y模型下近接施工對既有車站結構的變形影響規律，對計算結果進行了整理，研究了既有車站結構豎向（Z方向）的變形規律，位置如圖9所示。由于有的施工步相比前一施工步的計算結果變化不大，折線圖僅對比了變化大的四個關鍵施工步：step1為開挖至地下三層底板標高；step2為施工完新建16號線結構、逆筑部分頂板和樁柱；step3為開挖完預留的8m寬土體；step4為施工完逆筑部分的底板和上部結構。

圖9 變形研究位置示意

不同本構關系模型下既有車站結構沿Z軸規律如圖10所示，M-C模型下施工完step1后，既有車站結構東側墻柱的水平位移表現為下小上大，地下四層底板（Z=86.4m）位置的水平位移接近于零，地下三層中板（Z=95.36m）位置的水平位移為-0.1mm，地下二層中板（Z=105.01m）位置的水平位移為-0.3mm，地下一層中板（Z=110.56m）位置的水平位移為-0.2mm，地下一層頂板（Z=115.86m）位置的水平位移為-0.25mm。施工完step2后，既有車站結構的水平變形變化不大。施工完step3后，地下四層底板（Z=86.4m）位置的水平位移變化不大；地下三層中板（Z=95.36m）位置的水平位移為-0.5mm，這是因為地下四層底板受到開挖土體卸荷回彈和地下三層中板水平支撐的影響，所以該層側壁出現了先向左變形至-0.6mm，又向右變形；地下二層中板（Z=105.01m）位置的水平位移為0.2mm，這是因為地下二層中板從原來受到東西側土體側壓力的平衡狀態變為東側土體開挖后由逆筑板提供水平支撐的狀態；地下一層中板（Z=110.56m）位置的水平位移變化不大；地下一層頂板（Z=115.86m）位置的水平位移變化不大。施工完step4后，既有車站結構的水平變形變化不大。C-Y模型和M-C模型的既有車站結構沿Z軸變形規律相同，只是在數值上有所差異，且差別不大。

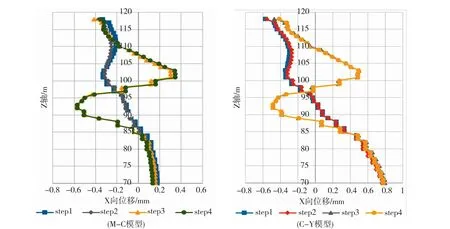
圖10 既有車站結構沿Z軸橫向變形規律

4.3 對既有車站結構的應力影響分析

4.3.1 開挖至地下三層底板標高

基坑開挖至地下三層底板標高，并預留了8m寬的土體在既有車站結構的東側。開挖完成后MC模型與C-Y模型下的最大主應力值的最大正值分別為1.33MPa、1.49MPa，最小主應力值的最大負值分別為5.29MPa、6.23MPa，其中最大主應力為拉力，出現在梁板和柱的連接處，最小主應力為壓力，從地下一層頂板到地下四層底板，結構板受到的壓應力逐漸增大，M-C模型與C-Y模型下的壓應力水平相當。

4.3.2 施工逆筑底板和上部結構

逆筑底板和上部結構施工完成后，M-C模型與C-Y模型下的最大主應力值的最大正值分別為1.29MPa和1.50MPa，M-C模型與C-Y模型下的最小主應力值的最大負值分別為-5.35MPa、-6.35MPa，由于施作結構的自重作用對結構模型受力影響不大。

5 結 論

（1）與Mohr-Coulomb模型相比，Cysoil模型所需的計算參數比較復雜，需要通過數值分析及現場試驗才能比較準確地確定相關參數。

（2）當選用Mohr-Coulomb模型時，由于該模型卸荷回彈時回彈模量和加載時的彈性模量相同，導致不真實的回彈變形，數值計算結果誤差較大。特別是進行基坑計算時回彈變形較大，采用Mohr-Coulomb模型基坑底部隆起很大，造成基坑周邊地表出現隆起，計算結果失真；而Cysoil模型可以有效解決基坑周邊地表的異常隆起現象，相對更加真實 地反映基坑開挖導致的地層變形規律。

（3）通過Mohr-Coulomb模型和Cysoil模型在近接施工中對既有車站結構的變形及受力特征影響規律的研究，可以看出兩種模型下既有結構力學響應規律相同，只是在數值上有所差異，且差別不大，在具體工程設計中，若僅分析近接施工對既有構筑物的影響，仍可采用M-C模型。