低溫柔性管道關鍵結構層的多目標優化設計

英璽蓬，曹慧鑫，楊志勛，楊 亮，劉淼兒，范嘉堃，李方遒，閻 軍

(1. 大連理工大學 工程力學系 工業裝備結構分析國家重點實驗室，遼寧 大連 116024; 2. 哈爾濱工程大學 機電工程學院，黑龍江 哈爾濱 150001; 3. 中海石油氣電集團技術研發中心，北京 100028)

液化天然氣是一種相對綠色環保、極具潛力的清潔能源，可對我國“碳達峰”戰略目標的實現起到關鍵作用[1]。海上浮式液化天然氣(floating liquefied natural gas，簡稱FLNG)裝置系統是一種集天然氣的液化、存儲和裝卸為一體的新型海上浮式液化天然氣生產系統[2-3]，具有集成化程度高、方便可靠等特點[4]。低溫柔性管道是FLNG系統的核心裝備之一，主要用于船只間的串靠連接，典型FLNG系統串靠連接方式如圖1所示[3]。

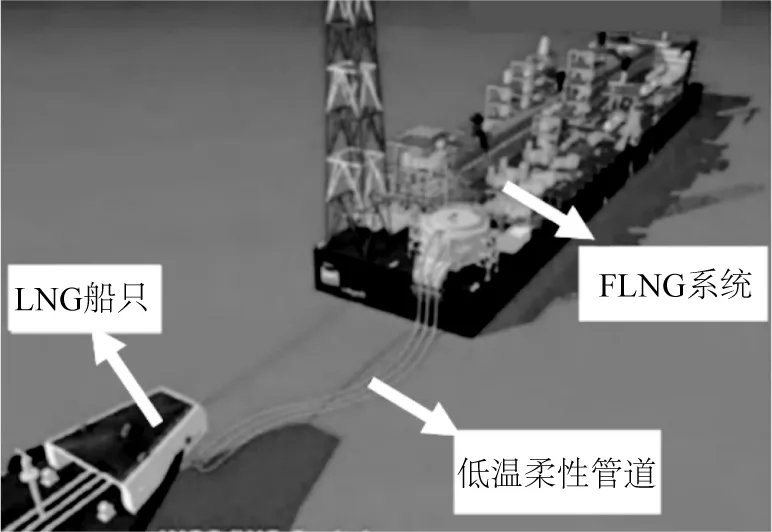
圖1 典型的FLNG串靠系統Fig. 1 Typical FLNG system in series connection

目前，國內外學者針對低溫柔性管道結構已開展了一定的研究。楊亮等[3]對FLNG低溫軟管的應用前景進行了系統調研，對目前的低溫軟管結構形式和關鍵技術進行了總結。除了在海洋氣田開發中的重要作用外，低溫軟管在浮式船岸傳輸與船舶加注等方面也有著巨大的應用前景。張進等[5]對低溫軟管的標準規范以及國外主流低溫軟管公司的產品進行了梳理，對其結構及性能特點進行了綜述，為我國低溫軟管的設計和制造提供了有益參考。在結構分析與性能研究方面，Yang等[6]基于有限元模擬方法對低溫軟管內襯波紋管結構的力學性能進行了機理研究及靈敏度分析，并基于不同優化算法對其進行了優化設計。Trelleborg公司針對FLNG系統中的串靠連接模式，研制出了一種新型的低溫柔性管道結構形式，類似于“管中管”的設計概念，其結構具有較好的密封性能與保溫性能，可以滿足惡劣海況下的輸送需求[7-8]。Srivastava等[9]和Buitrago等[10]基于低溫試驗的方法對低溫柔性管道內襯波紋管結構進行拉伸、彎曲、扭轉、內壓等工況下力學性能的研究，并總結出了金屬波紋管的結構尺寸對其力學性能的靈敏度影響規律。但在已有文獻中，大多是僅針對低溫柔性管道中的內襯波紋管結構進行力學性能研究，而對于低溫柔性管道其他關鍵結構層(抗拉鎧裝層、輔助層等)的力學性能及其優化設計理論、求解方法的研究則相對空白。

典型的低溫柔性管道整體結構如圖2所示。由內到外分別為：內襯波紋管層、防磨層、抗拉鎧裝層、保溫層以及護套層。內襯層是低溫柔性管道的最內層結構，起到承受管道內壓和密封液化天然氣的作用，一般為316L不銹鋼材料的U型波紋管結構；防磨層在低溫柔性管道的各個金屬結構層之間，起到防磨作用，由薄纖維布螺旋纏繞而成；抗拉鎧裝層是由多個扁帶狀纖維小角度螺旋纏繞、密排而成，是整個管道中承受載荷的部分；保溫層起到隔絕熱量傳遞的作用，防止管道外壁結冰，一般為氣凝膠材料；護套層是整個管道的最外層，直接與海面接觸，起到保護整個管道、防止腐蝕的作用。其中，內襯波紋管層、抗拉鎧裝層屬于功能不同的承載層，保溫層、防磨層、護套層屬于輔助層。

圖2 低溫柔性管道結構形式Fig. 2 Structure of cryogenic flexible hose

在實際工程中，低溫柔性管道主要應用于深遠海的天然氣開發，其環境工況往往較為惡劣，將持續受到風、浪、流等載荷作用。在低溫柔性管道的結構設計中，根據低溫柔性管道規范[11]中的要求，需要具有較強的軸向抗拉伸性能和較好的橫向彎曲柔順性，同時為防止管道外壁結冰進而影響管道的結構力學性能，還需使管道的隔熱性能最強并控制成本最低。綜上所述，需對低溫柔性管道進行多目標優化設計。此外，針對低溫柔性管道這種非黏結結構，通常可采用控制失效模式的設計方法。在結構的定量設計過程中，引起同一失效模式的荷載應該取最大值，且應該針對最先發生的結構破壞形式進行分析校核并提出控制策略以及優化設計方案[12-14]。本文以低溫柔性管道結構作為研究對象，將其按照實際工程應用中的不同功能解耦成不同結構層，包括內襯層(對應最小彎曲半徑失效)、抗拉鎧裝層(對應拉伸失效)以及輔助層(對應最小彎曲半徑失效)三個關鍵結構。分別基于神經網絡模型(RBF)、Kriging模型以及響應面模型(RSM)方法建立其力學響應分析的代理模型，并比較不同建模方法的準確度。在優化設計中，對于內襯層結構，以質量及彎曲剛度最小為優化目標；對于抗拉鎧裝層結構，以質量最小及拉伸剛度最大為優化目標；對于輔助層結構，以質量、彎曲剛度及傳熱速率最小為優化目標，基于遺傳算法分別對低溫柔性管道關鍵結構層進行多目標優化設計。最終得到了低溫柔性管道不同結構層的Pareto解集，可根據不同工程應用中的需求從解集中選擇符合實際要求的優化設計[15]，為低溫柔性管道的結構設計提供了理性的設計方法。

1 低溫柔性管道結構的代理模型及優化方法

1.1 代理模型建模方法

代理模型方法是工程上針對復雜結構較為常用的優化方法之一。其原理是用一個計算量較小的數學模型替換原復雜結構，通過一組變量與對應的輸出數據搭建近似的映射關系，將擬合出的近似函數替代原真實模型的物理過程[16]。響應面法(RSM)是最具代表性的建立代理模型方法[16]，其原理是通過一系列確定性試驗，用多項式函數來近似隱式極限狀態函數，在不降低計算精度的情況下簡化模型的計算量, 適用于線性問題的建模與計算[17]。在響應面法(RSM)的基礎上，Kriging模型和神經網絡模型(RBF)建模方法陸續出現并逐漸應用于各類優化問題中[16]。Kriging模型是一種插值模型，對于非線性問題的擬合精度較好，并且具有較好的約束處理能力，是一種通用的建模方法[16-17]。神經網絡模型(RBF)是基于徑向基函數的建模方法，具有最佳逼近和全局最優的優勢，訓練方法快速簡便、成本較低，具有良好的收斂能力，典型的神經網絡(RBF)建模方法流程如圖3所示[16]。

圖3 典型的神經網絡(RBF)建模方法流程Fig. 3 Typical neural network (RBF) modeling method

為進行低溫柔性管道關鍵結構層的多目標優化設計，分別基于神經網絡模型(RBF)、Kriging模型、響應面模型(RSM)三種方法建立低溫柔性管道三個關鍵結構層的各項力學性能的代理模型，并分別比較其準確度，進而篩選出適用于低溫柔性管道結構的近似代理模型。

1.2 優化算法

遺傳算法(genetic algorithm)是一種基于群體進化的計算模型，通過群體中個體之間的繁殖、變異、競爭等方法進行信息交換、優勝劣汰，從而逐步逼近問題的最優解[16-17]。其中，對個體的遺傳操作主要是通過選擇(繁殖)、交叉和變異(突變)三個基本的遺傳算子實現[16-17]。

在各種遺傳算法中，NSGA算法(non-dominated sorting genetic algorithm)是解決多目標優化問題中較為常見的方法。基于非支配分層策略，NSGA算法可使得更好的個體有更大的機會遺傳到下一代。在多目標優化求解的過程中，NSGA算法保持了群體的多樣性，其Pareto解集上的個體均勻分布，防止了個別超級個體的過度繁殖。NSGA-II優化算法是NSGA的改良算法，其優點在于探索性良好，在非支配排序中Pareto解集的前進能力更強。克服了前期NSGA算法的缺點，使得NSGA-II算法的優化效率更高、解集前沿更加清晰[16-17]。因此，本文選用遺傳算法中的NSGA-II優化算法進行低溫柔性管道關鍵結構層的多目標優化設計。

1.3 優化設計流程

如前文所述，可將低溫柔性管道按其力學性能與功能特點分為內襯波紋管層、抗拉鎧裝層、輔助層三個關鍵結構層。分別基于神經網絡模型(RBF)、Kriging模型、響應面模型(RSM)三種建模方法建立上述各結構層的代理模型，通過比較驗證各代理模型對于不同結構層力學響應的準確性。并基于遺傳算法中的NSGA-II優化算法分別對內襯波紋管層、抗拉鎧裝層、輔助層三個結構層進行多目標優化設計。最后得到低溫柔性管道各層結構尺寸參數的Pareto優化解集，按照結構多目標優化設計的有限解理論[15, 18-21]，根據工程需要選用解集中的優化設計方案。本文低溫柔性管道關鍵結構層的多目標優化設計流程如圖4所示。

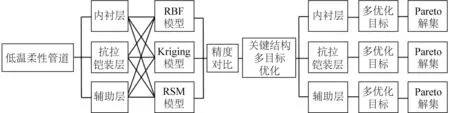
圖4 低溫柔性管道多目標優化設計流程Fig. 4 Multi-objective optimization design process of cryogenic flexible hose

2 低溫柔性管道關鍵結構層的多目標優化

本文所建立的低溫柔性管道有限元模型如圖5所示，共有73 779個網格。有限元模型長度設置為1 710 mm，包括內襯U型波紋管層、抗拉鎧裝層、輔助層等結構。

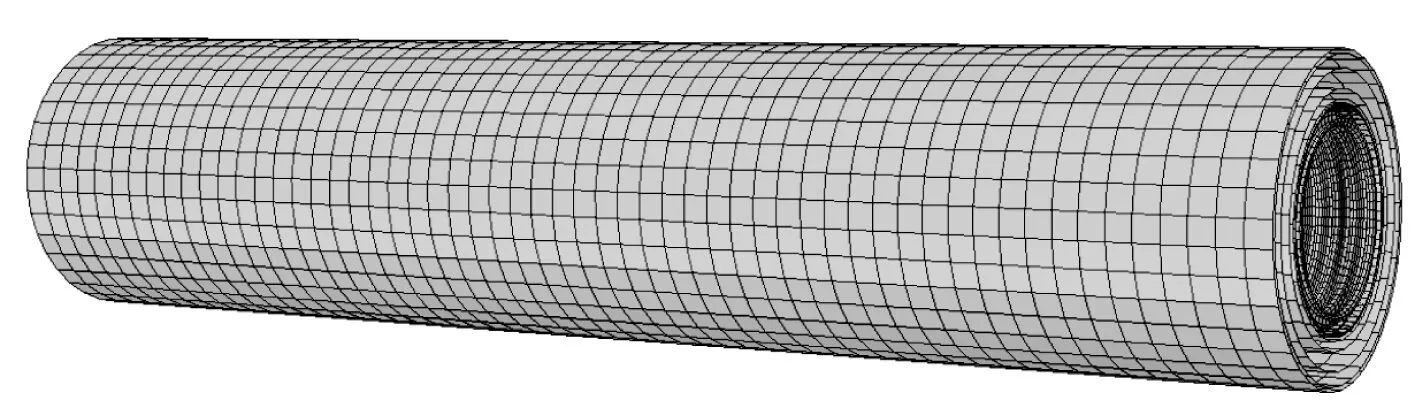
圖5 低溫柔性管道的有限元模型Fig. 5 Finite element model of cryogenic flexible hose

2.1 內襯層的多目標優化

低溫柔性管道內襯U型波紋管截面結構如圖6所示。其中，P為波紋管的波距，H為波紋管的波高，T1為波紋管的壁厚。一般地，U型波紋管的截面結構由其波距P、波高H和壁厚T1所確定，因此取以上三個結構參數作為低溫柔性管道內襯層多目標優化的設計變量。

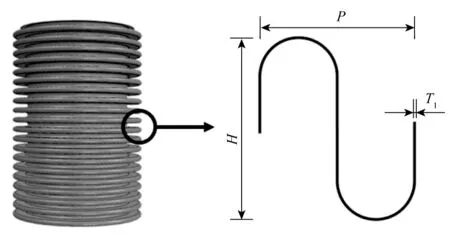
圖6 內襯U型波紋管截面結構示意Fig. 6 Section structure of lined U-shaped bellows

考慮到U型波紋管的實際工藝水平與規范要求[22-23]，分別取波距P的范圍為6.0～12.0 mm、波高H的范圍為7.0～13.0 mm、壁厚T1的范圍為0.8～1.2 mm。為方便計算，采用有限元分析軟件中的S4R殼單元建立內襯U型波紋管參數化模型，其材料為304不銹鋼(彈性模量為193 GPa、泊松比為0.3)。在實際工程應用中，內襯U型波紋管作為低溫柔性管道的最內層結構，決定著整個管道結構的最小彎曲半徑。應使得U型波紋管具有較小的彎曲剛度，進而保證整個管道的彎曲柔順性，并同時控制U型波紋管的制造成本。因此，在低溫柔性管道內襯層的多目標優化中，以內襯U型波紋管的彎曲剛度EI1最小(保證整管的彎曲柔順性)和質量m1最小(控制成本)作為兩個優化目標進行多目標優化，其多目標優化列式如式(1)所示。需要特別指出的是，波紋管的成本與材料用量、成型精度、工藝選擇等密切相關。為簡化計算，暫不考慮成型工藝等其他因素的影響，取成型后的材料用量，即質量作為成本的標識，抗拉鎧裝層與輔助層的成本做同樣處理。

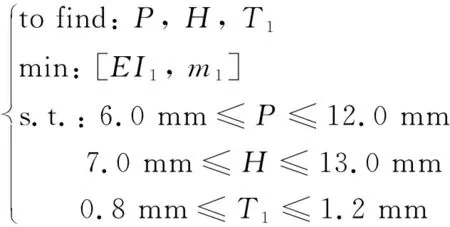
(1)

根據代理模型建模方法，分別采用神經網絡模型(RBF)、Kriging模型以及響應面模型(RSM)三種方法建立輸入變量與輸出變量的映射關系。基于參數化有限元模擬計算U型波紋管結構在6組波距P、6組波高H、5組壁厚T1下的彎曲剛度及質量，由此共獲得180組數據樣本。隨機取其中的90組數據建立代理模型，取余下的90組數據驗證其預測準確度，得到基于三種建模方法的代理模型及其預測的準確度(與有限元模擬結果相比)，如表1所示。由表1中數據可知，在低溫柔性管道內襯層結構的代理模型中，雖然神經網絡模型(RBF)的方差與響應面模型(RSM)的方差幾乎相等，但RBF模型的平均誤差均小于RSM模型；Kriging模型的方差與平均誤差均劣于RBF模型與RSM模型。由此可見，與其他兩種建模方法相比，RBF模型具有準確度好、穩定性強等優點。因此，選用神經網絡模型(RBF)建立低溫柔性管道內襯層結構的代理模型。

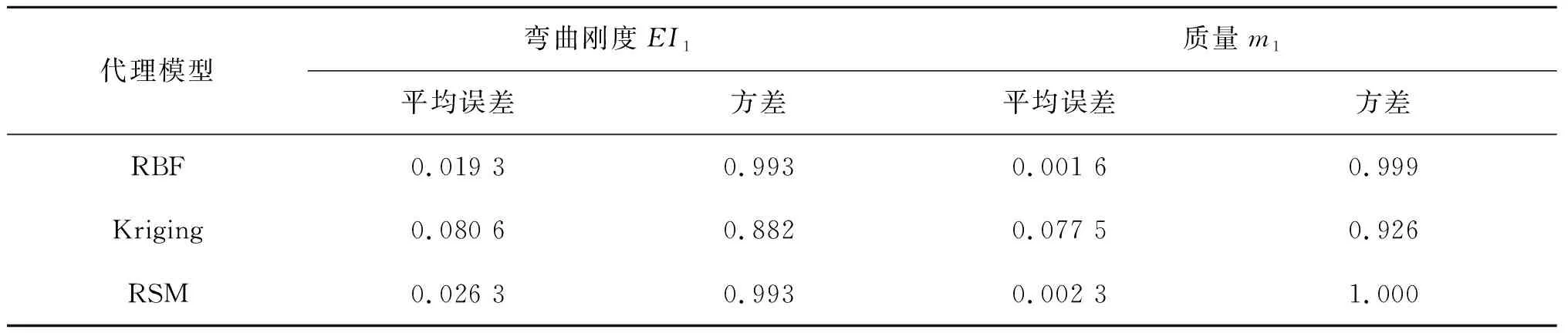
表1 內襯層代理模型預測準確度對比(與有限元模型相比)Tab. 1 Precision comparison of agent models of lined U-shaped bellows (compared with FEM results)

在低溫柔性管道內襯層結構的多目標優化設計中，基于NSGA-II優化算法對其多目標優化問題進行計算求解。設置初始優化種群規模為90，遺傳代數為100，可基于NSGA-II優化算法計算出1 167個Pareto優化解集，所得Pareto解集如圖7所示。由圖7可知，在Pareto優化解集中，A點表示彎曲剛度最小的單目標優化時內襯U型波紋管的設計，此時彎曲柔順性最優；B點表示質量最小單優化目標時內襯U型波紋管的設計，此時質量最小(一定程度上表示制造成本最低)；C點則表示兼顧質量與彎曲剛度兩個目標時(坐標原點到Pareto前沿距離最短的設計點)，內襯U型波紋管結構的多目標優化設計。三個點分別代表的低溫柔性管道內襯波紋管層的結構設計方案如表2所示。

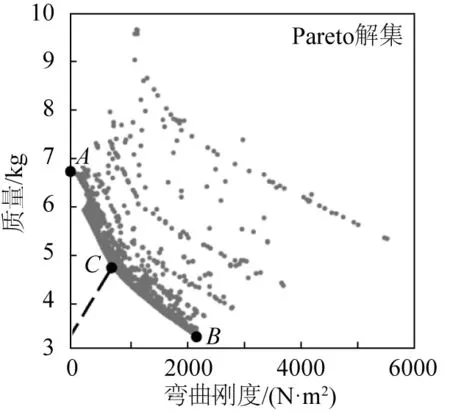
圖7 內襯層多目標優化的Pareto解集Fig. 7 Pareto solution for multi-objective optimization of lined U-shaped bellows

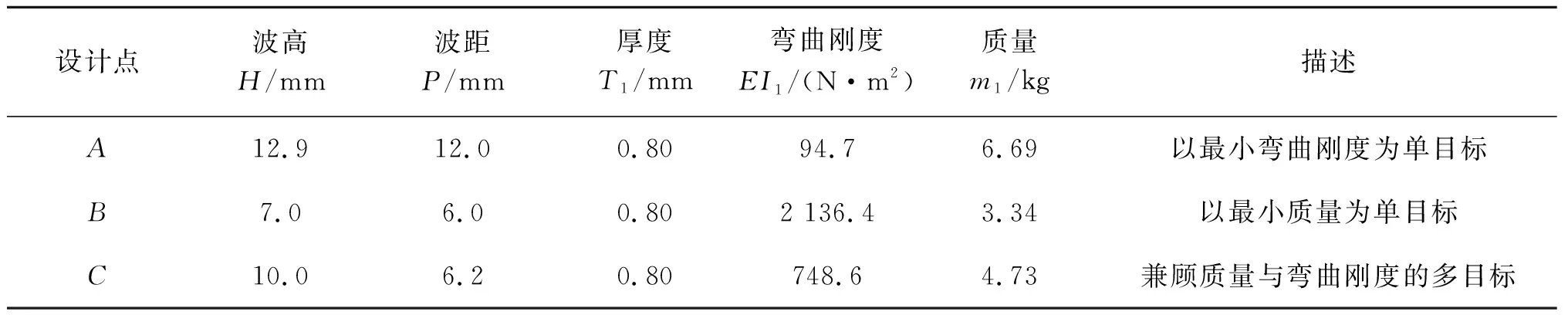
表2 低溫柔性管道內襯層代表性設計方案Tab. 2 Typical designs of lined U-shaped bellows of cryogenic flexible hose

從表2中的數據可以看出，雖然A點的彎曲剛度最小(94.7 N·m2)，但其質量最大，達到6.69 kg；而雖然B點的質量最小，為3.34 kg(僅為A點的一半)，但其彎曲剛度遠遠大于A點對應的彎曲剛度(是A點彎曲剛度的22倍)；而C點較好地兼顧了質量與彎曲剛度的設計要求，可以更好地滿足低溫柔性管道內襯波紋管結構的使用要求。同時，從上述分析可以看出，對于Pareto前沿上的優化設計點，當彎曲剛度變優時，必然引起質量目標的劣化；反之亦然。這體現了多目標優化中Pareto前沿的工程設計意義。

2.2 抗拉鎧裝層的多目標優化

本節進行低溫柔性管道結構抗拉鎧裝層的多目標優化。抗拉鎧裝層結構如圖8所示。其中，α為抗拉鎧裝層扁帶狀纖維的螺旋纏繞角度，T2為扁帶狀纖維的厚度。抗拉鎧裝層結構的力學性能是由其扁帶狀纖維螺旋纏繞角度α和厚度T2所確定，因此取以上兩個結構參數作為低溫柔性管道抗拉鎧裝層多目標優化的設計變量。

圖8 抗拉鎧裝層螺旋纏繞結構示意Fig. 8 Structure of spiral armored layer

考慮到抗拉鎧裝層的工程應用需要與實際工藝水平[24]，分別取扁帶狀纖維螺旋纏繞角度的范圍為30°～ 40°、壁厚T2的范圍為1.0～3.0 mm。為方便計算，基于有限元分析軟件中的C3D8R實體單元建立抗拉鎧裝層結構的參數化模型，選用碳纖維編織材料(彈性模量為84 GPa、泊松比為0.36)。在實際工程應用中，抗拉鎧裝層是低溫柔性管道的重要承載結構，其主要承擔軸向載荷。當低溫柔性管道在位作業時，海面上的風、浪、流等環境載荷較為惡劣，要求抗拉鎧裝層具有較強的拉伸剛度，進而有效抵抗管道整體的軸向變形，防止因管道整體變形過大而導致的失效。同時，管道設計也要求控制抗拉鎧裝層的制造成本(與內襯層相同，本節中亦采用抗拉鎧裝層的質量作為成本標識)。因此，在低溫柔性管道抗拉鎧裝層的多目標優化中，以抗拉鎧裝層的拉伸剛度EA最大(保證整管具有足夠的拉伸剛度)和質量m2最小(控制成本)作為兩個優化目標進行多目標優化，其多目標優化列式如式(2)所示。

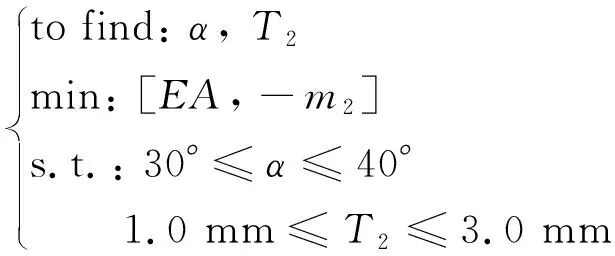
(2)

與內襯層類似，分別采用神經網絡模型(RBF)、Kriging模型以及響應面模型(RSM)三種方法建立抗拉鎧裝層力學性能的代理模型。基于參數化建模，計算出在10組螺旋纏繞角度α、8組厚度T2組合下抗拉鎧裝層的拉伸剛度及質量，由此共獲得80組數據樣本。隨機取其中的40組數據建立代理模型，取余下的40組數據驗證其預測準確度，得到基于三種建模方法的代理模型及其預測的準確度(與有限元模擬結果相比)，如表3所示。

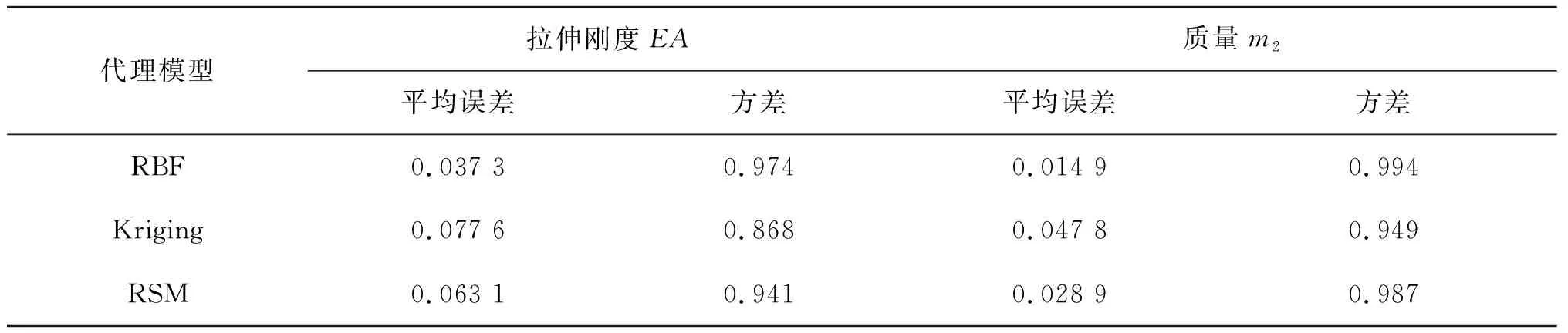
表3 抗拉鎧裝層代理模型準確度對比(與有限元模型相比)Tab. 3 Precision comparison of agent models of spiral armored layer (compared with FEM results)

由表3中數據可知，在低溫柔性管道抗拉鎧裝層結構的代理模型中，與其他兩種建模方法相比，神經網絡模型(RBF)的近似準確度最好、穩定性最強。因此，本節同樣選用神經網絡模型(RBF)建立低溫柔性管道抗拉鎧裝層結構的代理模型。

在低溫柔性管道抗拉鎧裝層結構的多目標優化設計中，同樣基于NSGA-II優化算法對其多目標優化問題進行計算求解。設置初始優化種群規模為40，遺傳代數為100，可基于NSGA-II優化算法計算出1 237個Pareto優化解集，所得Pareto解集如圖8所示(為在圖中更直觀得到Pareto最優前沿，此處將質量m2最小化處理為負質量(-m2)最大化)。由圖9可知，在Pareto優化解集中，A點表示拉伸剛度最大的單目標優化時抗拉鎧裝層的設計，此時抵抗管道整體軸向變形的能力最強；B點表示質量最小單優化目標時抗拉鎧裝層的設計，此時質量最小(一定程度上表示制造成本最低)；C點則表示兼顧質量與拉伸剛度兩個目標時(坐標原點到Pareto前沿距離最短的設計點)，抗拉鎧裝層結構的多目標優化設計。

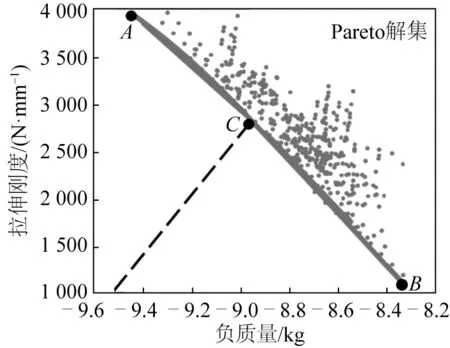
圖9 抗拉鎧裝層多目標優化的Pareto解集Fig. 9 Pareto solution for multi-objective optimization of spiral armored layer

三個點分別代表的低溫柔性管道抗拉鎧裝層的結構設計方案如表4所示。從表4中的數據可以看出，雖然A點的拉伸剛度最大(3 843.7 N/mm)，但其質量也最大，為9.41 kg；而雖然B點的質量最小(僅為8.36 kg)，但其拉伸剛度遠遠小于A點對應的拉伸剛度(僅為A點拉伸剛度的27%)；而C點較好地兼顧了質量與拉伸剛度的設計要求，可以更好地滿足低溫柔性管道抗拉鎧裝層結構的使用要求。從上述分析亦可看出，對于Pareto前沿上的優化設計點，當拉伸剛度變優時，必然引起質量目標的劣化；反之亦然。

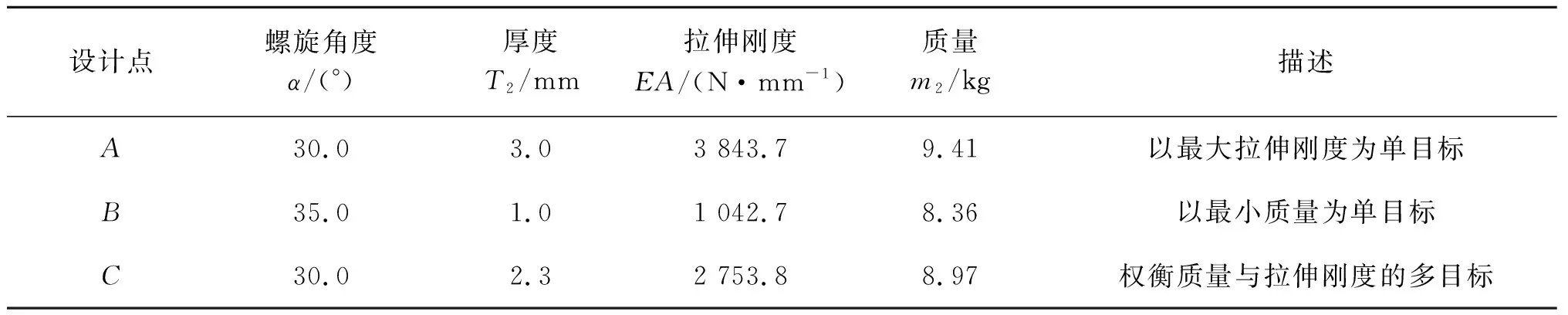
表4 低溫柔性管道抗拉鎧裝層代表性設計方案Tab. 4 Typical designs of spiral armored layer of cryogenic flexible hose

2.3 輔助層的多目標優化

本節進行低溫柔性管道結構輔助層的多目標優化。輔助層結構包括防磨層、護套層、保溫層，其結構可簡化成如圖10所示的薄壁圓筒，對應的厚度分別為T3、T4、T5。其中，保溫層主要起到隔絕內外熱量傳遞、防止管道外壁結冰的作用，可通過熱傳導理論直接求出保溫層最小厚度T5，進而以最小的成本實現隔絕熱量傳遞的效果，因此本文不針對保溫層進行優化設計。除保溫層外，防磨層和護套層的結構都是由其對應的厚度T3、T4所確定，因此取以上兩個結構參數作為低溫柔性管道輔助層多目標優化的設計變量。

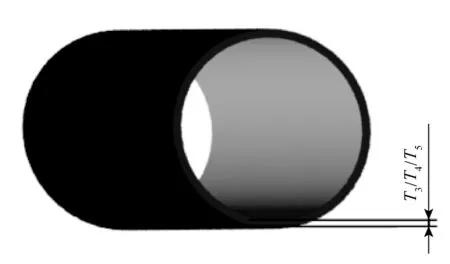
圖10 輔助層結構參數示意Fig. 10 Structure of auxiliary layers

考慮到輔助層的防磨層與護套層在實際工程應用中的功能需要[25]，分別取防磨層厚度T3的范圍為2.0～6.0 mm、護套層厚度T4的范圍為1.0～3.0 mm。為方便計算，采用有限元分析軟件中的S4R殼單元建立輔助層結構的參數化模型，選用橡膠材料(彈性模量為78 GPa、泊松比為0.47)。在實際應用中，防磨層主要起到防止各個金屬層結構之間的摩擦、磨損作用，而護套層則主要起到保護整個管道、防止腐蝕的作用。在滿足防磨層和護套層自身功能的基礎上，應使得其具有較好的彎曲柔順性，進而保證整個管道的彎曲柔順性，并同時控制防磨層和護套層的制造成本。此外，由于防磨層和護套層屬于非金屬材料，還希望其起到一定隔絕熱量傳遞的作用。因此，在低溫柔性管道輔助層的多目標優化中，以輔助層的彎曲剛度EI2最小(保證整管的彎曲柔順性)、質量m3最小(控制成本)(與內襯層相同，本節中亦采用輔助層的質量作為成本標識)以及熱傳遞速率R最小(保證整管的隔熱性能)作為三個優化目標進行多目標優化，其多目標優化列式如式(3)所示。

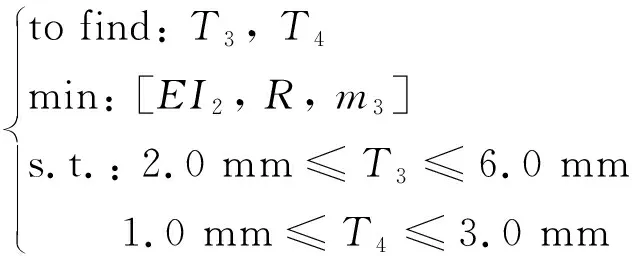
(3)

類比內襯層、抗拉鎧裝層，分別采用神經網絡模型(RBF)、Kriging模型以及響應面模型(RSM)三種方法建立輔助層的代理模型。基于參數化有限元模擬計算出輔助層在10組防磨層厚度T3、10組護套層厚度T4下的彎曲剛度EI2、質量m3以及熱傳遞速率R，由此共獲得100組數據樣本。隨機取其中的50組數據建立代理模型，取余下的50組數據驗證其預測準確度，得到基于三種建模方法的代理模型結果及其預測的準確度(與有限元模擬結果相比)，如表5所示。

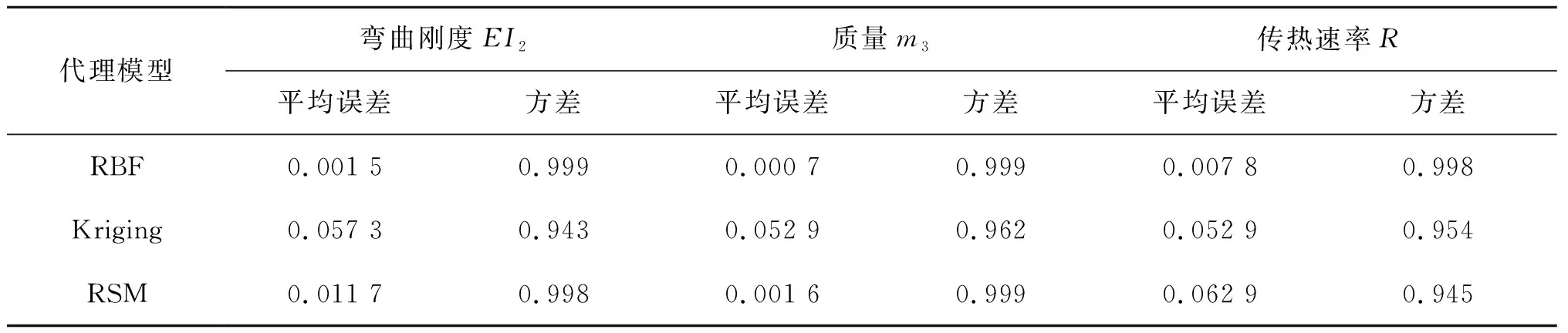
表5 輔助層代理模型準確度對比(與有限元模型相比)Tab. 5 Precision comparison of agent models of auxiliary layers (compared with FEM results)

由表5數據可知，在低溫柔性管道輔助層結構的代理模型中，與其他兩種建模方法相比，神經網絡模型(RBF)的平均誤差與方差均是最優的。因此，本節同樣選用神經網絡模型(RBF)建立低溫柔性管道輔助層的代理模型。

在低溫柔性管道輔助層的多目標優化設計中，基于NSGA-II優化算法對其多目標優化問題進行求解。設置初始優化種群規模為50，遺傳代數為100，可基于NSGA-II優化算法計算出2 552個Pareto優化解集，優化所得Pareto解集如圖11所示。

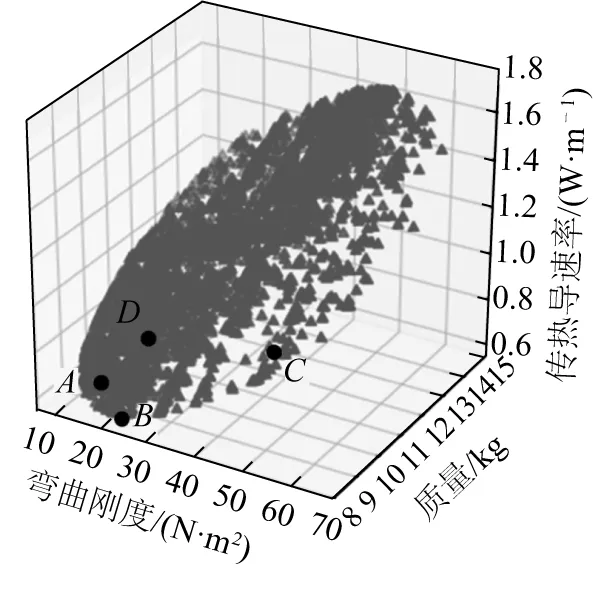
圖11 輔助層多目標優化的Pareto解集Fig. 11 Pareto solution for multi-objective optimization of auxiliary layers

從Pareto優化解集中可選出部分具有代表性的低溫柔性管道輔助層設計方案，如表6所示。 從表6中的數據可以看出，雖然A點的彎曲剛度最小(10.4 N·m2)，但其傳熱速率最大，質量也處于明顯劣勢；而B點的質量雖然最小(僅為8.15 kg)，但其彎曲剛度是A點對應彎曲剛度的2倍以上；而C點的傳熱速率雖然最小，但其彎曲剛度是A點對應彎曲剛度的3倍以上，質量也處于劣勢；而D點較好地兼顧了彎曲剛度、質量、傳熱速率的設計要求，可以更好地滿足低溫柔性管道輔助層結構的使用要求。

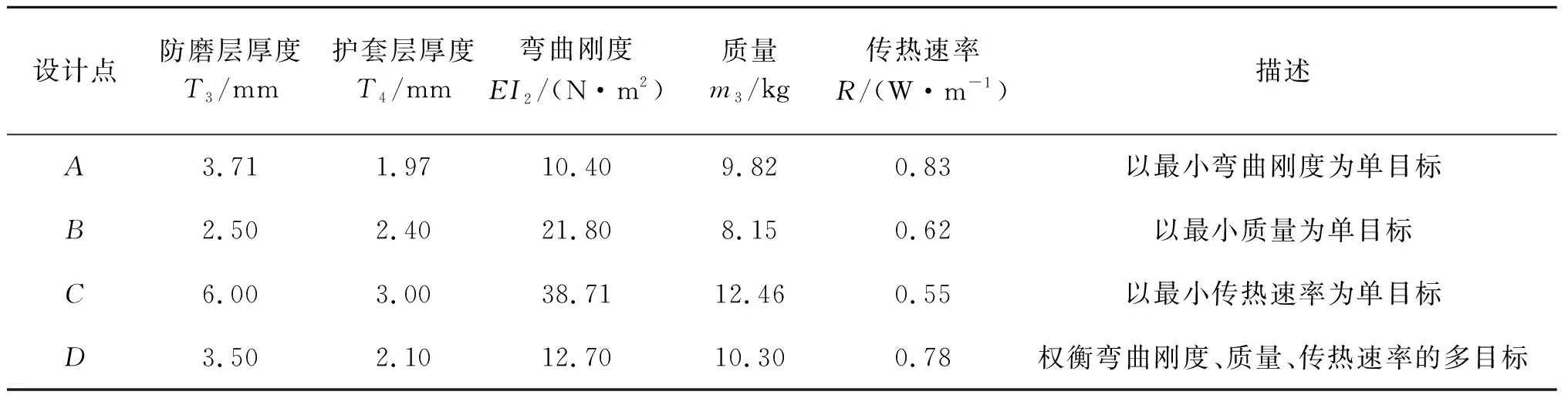
表6 低溫柔性管道輔助層部分代表性設計方案Tab. 6 Typical designs of auxiliary layers of cryogenic flexible hose

3 結 語

以海上浮式液化天然氣裝置系統(FLNG)的低溫柔性管道為研究對象，針對其多材料、多層復合的結構設計難點，將其按照不同功能解耦成內襯層、抗拉鎧裝層及輔助層三個關鍵結構層。基于神經網絡模型(RBF)、Kriging模型以及響應面模型(RSM)三種建模方法建立了上述三個結構層響應分析的代理模型，并通過模型準確度的比較，發現神經網絡模型(RBF)的誤差均最小。在優化設計中，基于遺傳算法中的NSGA-II算法分別對低溫柔性管道的內襯層、抗拉鎧裝層、輔助層三個關鍵結構層分別進行多目標優化設計，得到了各個結構層的Pareto優化解集。可根據實際工程應用中的特定需求，在Pareto優化解集里找到各個結構層的最優解。本文的研究工作為低溫柔性管道的結構提供了關鍵設計參數及理性的設計方法。

目前主要對機械載荷下低溫柔性管道的多目標優化設計進行了研究，未來還需充分考慮因超低溫環境造成的溫度應力以及成型工藝參數等對管道性能的影響，研究超低溫環境下低溫柔性管道各結構層材料的性能變化規律；并考慮在拉伸、彎曲、扭轉、多工況復合載荷作用下進行低溫柔性管道的結構力學分析與優化設計。