基于串級雙向長短時記憶神經網絡的測井數據重構

周 偉 趙海航 蔣云鳳 易 軍 賴富強

(重慶科技學院智能技術與工程學院，重慶 401331)

0 引言

測井數據是進行地下儲層解釋與評價的重要基礎，對于指導油氣藏勘探、開發具有重要意義。在實際測井過程中，測井儀器故障、井壁垮塌等因素導致測井數據失真或者缺失。由于重新測井成本高昂，且對于許多已做過固井的油氣井來說，重新測井工程難度極大。測井數據失真或缺失給油氣藏開發和評價帶來了巨大挑戰。因此，如何重構失真或缺失的測井曲線已成為新挑戰[1-3]。

近年來，許多數據驅動方法被提出來并應用于地質參數估計及油藏描述等方面，如人工神經網絡(Artificial Neural Network，ANN)[4-5]、模糊邏輯模型(Fuzzy Logic Model，FLM)[6]、決策樹(Decision-making Tree，DT)[7]和支持向量機(Support Vector Machine，SVM)[8]等。由于測井數據具有明顯的時間或空間序列特征，數據之間存在長序列依賴關系，上述機器學習方法無法有效提取測井數據的依賴關系，且存在計算效率低或易過擬合等缺點[8]，因此它們在一定程度上不能完全適用于基于測井資料的地質建模或巖性識別[9]。

隨著人工智能技術的發展，循環神經網絡(Recurrent Neural Network，RNN)在地球科學各領域的良好應用而受到廣泛關注[10]。由于RNN需要為每一步保持一個激活向量，容易在訓練階段出現梯度爆炸和消失問題[11]。長短時記憶(Long Short-Term Memory，LSTM)神經網絡是一種特殊的RNN結構[12]，通過正則化項約束權值范數，使其不至于過大，在一定程度上遏制了RNN的梯度爆炸和消失問題的發生。考慮到測井數據通常在同一巖性段內呈現平滑變化特征，測井數據與LSTM網絡之間有天然的內在匹配特性，因此LSTM網絡已被應用于測井數據重構方法研究[13-14]。由于單向LSTM網絡方法只考慮數據信息在單方向序列的相關性，忽略了缺失點后序數據的影響，不利于對測井數據的精準預測。

于是，雙向長短時記憶(Bidirectional LSTM，Bi-LSTM)神經網絡[15-18]應運而生，它利用另一個在序列中向后移動的LSTM完成雙向時序學習，該結構既能表征過去的趨勢，也能預測未來發展方向，對于整段測井數據缺失的情況，具有天然的雙向時序數據重構優勢。周雪晴等[19]提出基于Bi-LSTM網絡的流體高精度識別新方法，利用Bi-LSTM網絡提取井下測井曲線隨深度的變化趨勢及前后關聯特征，提高流體識別能力。周欣等[20]提出一種基于雙向門控循環單元神經網絡的聲波測井曲線重構技術，充分利用測井數據中的前后序列關聯性補全缺失的聲波測井曲線。王俊等[21]提出基于深度雙向RNN的儲層孔隙度預測方法，利用雙向RNN建立測井數據與儲層孔隙度之間的非線性映射關系，提高了模型預測的準確性。但上述方法在具體應用時，都存在一定缺陷：一是每次預測多條曲線，待測曲線之間干擾較大。二是模型缺乏靈活性和適應性，一旦模型訓練完成，無法將當前井已補全的測井曲線用于剩余測井曲線的補全。不能充分考慮當前井測井曲線之間的影響關系，即模型無法在補全過程中做優化。

為此，本文提出一種串級雙向長短時記憶(CBi-LSTM)網絡的測井數據重構方法，利用缺失數據點的前趨與后繼之間的雙向關聯性，提取缺失數據點的前趨與后繼中的關鍵特征信息對缺失數據點進行重構，采用串級更新策略，將獲得的估計值與已知測井曲線合并為新的輸入，完成對缺失測井數據塊的重構。

1 基于Bi-LSTM網絡的數據重構法原理

1.1 長短時記憶網絡

LSTM網絡是RNN的改進算法，通過門機制將短期記憶與長期記憶結合起來，彌補RNN只能記憶短期的歷史輸入信息而無法實現長期記憶的缺陷，在一定程度上解決了網絡的梯度消失和梯度爆炸。LSTM網絡保留了RNN的鏈式結構，由一系列遞歸鏈接的記憶區塊的子網絡構成，其中關鍵結構為交互層中的3個門層，即輸入門、輸出門、遺忘門(圖1)。

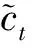
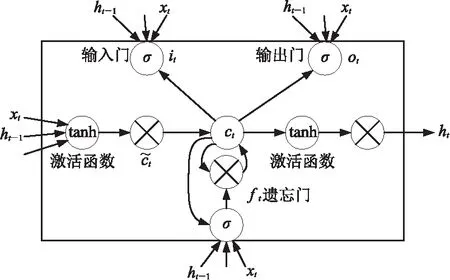
圖1 LSTM模型示意圖

利用上述結構，在各時間點t都可得到對應的隱藏層狀態序列，從而獲得每一個時間步輸出的結果。由于LSTM網絡只能單方向地處理數據，無法考慮缺失點后面數據的影響。另外，模型缺乏魯棒性，使用過程無法利用當前井補全的缺失曲線和已知曲線作為新的輸入，來補全剩余缺失曲線，且無法充分考慮當前井曲線之間相關性。

1.2 雙向長短時記憶網絡

在實際測井時，采樣間隔往往較小，通常可低至0.1m。然而從地層角度而言，不同深度地層之間相互影響的范圍高達30m，甚至50m[22]。因此，每個數據點周圍相互有影響的范圍包含數據點可多達240～400個，不僅包括當前地層以上部分，還包括當前地層以下部分，這就意味著測井曲線重構是典型的具有長期雙向(空間)相關性的序列數據分析問題。相對LSTM模型，Bi-LSTM模型更適合處理這類問題。為了將當前地層以下的測井數據信息的影響考慮到建模中，本文使用Bi-LSTM網絡，它由一個前向LSTM模型與一個后向LSTM模型連接組成。作為時序相反的兩個LSTM網絡，前向LSTM網絡可獲取缺失序列之前儲層段的信息，后向LSTM網絡可獲取缺失序列之后儲層段的信息。該模型能從前、后兩方面充分提取上、下儲層段的信息，從而提高模型效果。

圖2為Bi-LSTM模型示意圖，從中可看出Bi-LSTM網絡是由兩層LSTM網絡組成：第一層認左邊作為起始輸入，在測井曲線重構時可理解成從當前采樣點前一段序列開始輸入；第二層是認右邊作為起始輸入，在測井曲線重構時可理解成從當前采樣點后一段序列作為輸入，反向開展與第一層相同的處理。此時，yt-1、yt及yt+1為前、后兩個LSTM網絡共同作用的結果。

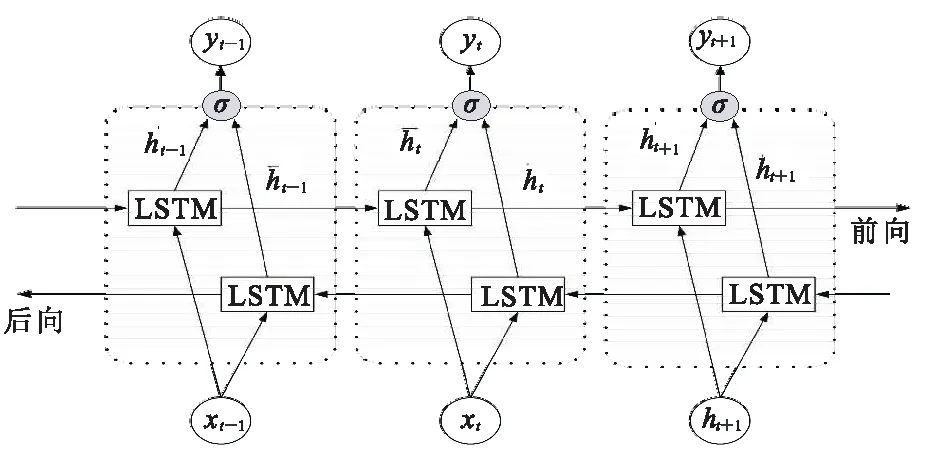
圖2 Bi-LSTM模型示意圖

在將Bi-LSTM網絡應用到測井曲線數據的重構過程中，雖然Bi-LSTM網絡完美地解決了LSTM網絡只能按照從前到后的順序處理數據，無法融合后序數據信息的問題，但模型缺乏靈活性。模型一旦訓練完成，在補全過程中無法進行優化，且未能利用當前井補全的測井曲線數據繼續補全剩余曲線，導致模型缺乏適應性。

1.3 串級雙向長短時記憶神經網絡

針對Bi-LSTM網絡存在的問題，提出了CBi-LSTM網絡，其原理如圖3所示。

CBi-LSTM網絡模型借鑒串級控制系統思想，每次補全缺失曲線中的一條。在第一級，利用完整的測井曲線自然電位(SP)和井徑(CAL)測井數據完成缺失曲線聲波時差(AC)的補全；在第二串級將補全的AC與已知的SP及CAL測井曲線結合，作為新的輸入，補全自然伽馬(GR)缺失曲線；最后，完成所有缺失曲線的重構。

可看出使用串級控制系統思想有以下優點。

(1)每次只補全缺失的一條曲線，減少了待重構曲線之間的相互干擾。

(2)提高模型的輸入兼容性。在每一級，可將補全的數據和已知數據進行合并作為新的輸入，利用當前井補全的測井曲線數據繼續補全剩余曲線中的一條，進一步提高了模型的適應性。

(3)模型訓練完成后，可從中間步直接進行下一條缺失曲線的重構。

(4)補全過程中，網絡共享各級的重構數據，每級只保留當前級預測數據，避免了數據冗余。

在引入串級系統的基礎上，對其中主干網絡結構進行改進，特征提取使用兩層Bi-LSTM網絡，并增加三層全連接層，進一步增強模型的表達能力。主干網絡結構如圖4所示，采用兩個隱狀態分別為80和100維的Bi-LSTM網絡和三層全連接層，采用丟棄操作，概率為30%。

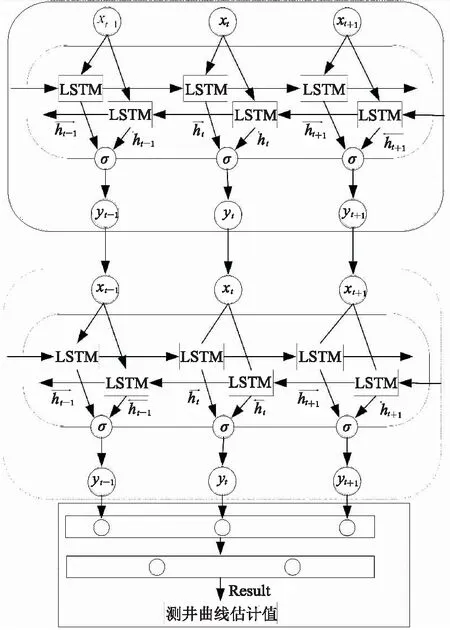
圖4 主干網絡結構框架

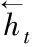
當前串級計算過程如下：

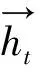
(1)

(2)

(3)

(4)

(5)

(6)

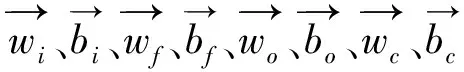
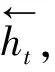
(7)

(8)

(9)

(10)

(11)

(12)

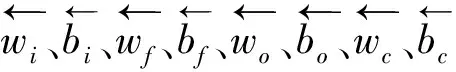
集團管理層每月召開一次戰略墻運營分析會，對真北指標進行內外部趨勢對比、競爭分析，評價醫院和部門長期目標、年度目標和年度戰略計劃達成情況。

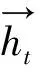
(13)

(4)完成兩個隱狀態計算結果后，將結果轉化成一維數據(yt)并傳入全連接層進行計算，過程為

(14)

resu1ti=f(Neti)

(15)

(16)

式中：Neti為激活函數f的輸入；wl1和wl2為全連接層待訓練權重；resulti為預測值；resultr為真實值。然后利用均方誤差Ek更新參數，優化網絡。

(5)最后傳入曲線的預測所缺失的值resulti。到下一級并和已知數據合并為新的輸入預測剩余缺失曲線中的一條，重復上述計算過程。

在CBi-LST網絡結構中，首先根據已知測井曲線訓練模型估計未知測井曲線中的1條，然后將獲得的估計值與已知測井曲線合并為新的輸入，作為下一級的輸入，再據此輸入估計剩余未知測井曲線中的1條。缺失曲線重構過程如圖5所示。

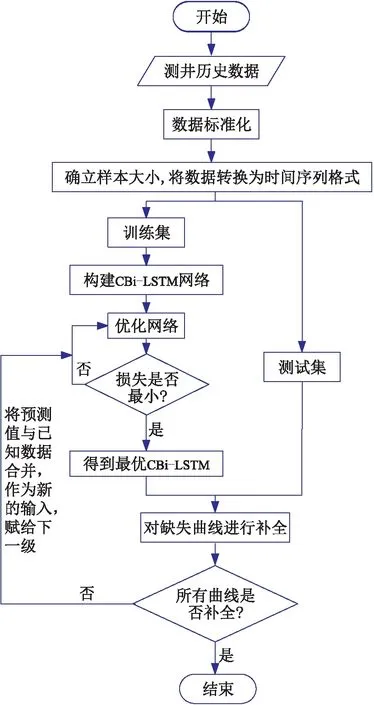
圖5 曲線重構流程圖

2 實驗研究

2.1 數據準備

采用蘇里格氣田4口直井測井數據開展實驗。這些井都記錄了多種測井數據，如AC、CAL、CNL(補償中子)、GR、SP、TH(放射性釷)、U(鈾)、K(鉀)等。為了驗證模型對測井數據的重構能力，實驗基于留一法補充相關文獻，即進行四次實驗，每次實驗將一口井作為實驗，其余三口井作為訓練數據，對模型進行訓練，最終用模型生成實驗井的測井曲線。

實驗中直井的探測深度為3300～3800m，對應該深度范圍的AC和GR測井曲線被人工刪除，用于模擬缺失部分的測井曲線(圖6)。

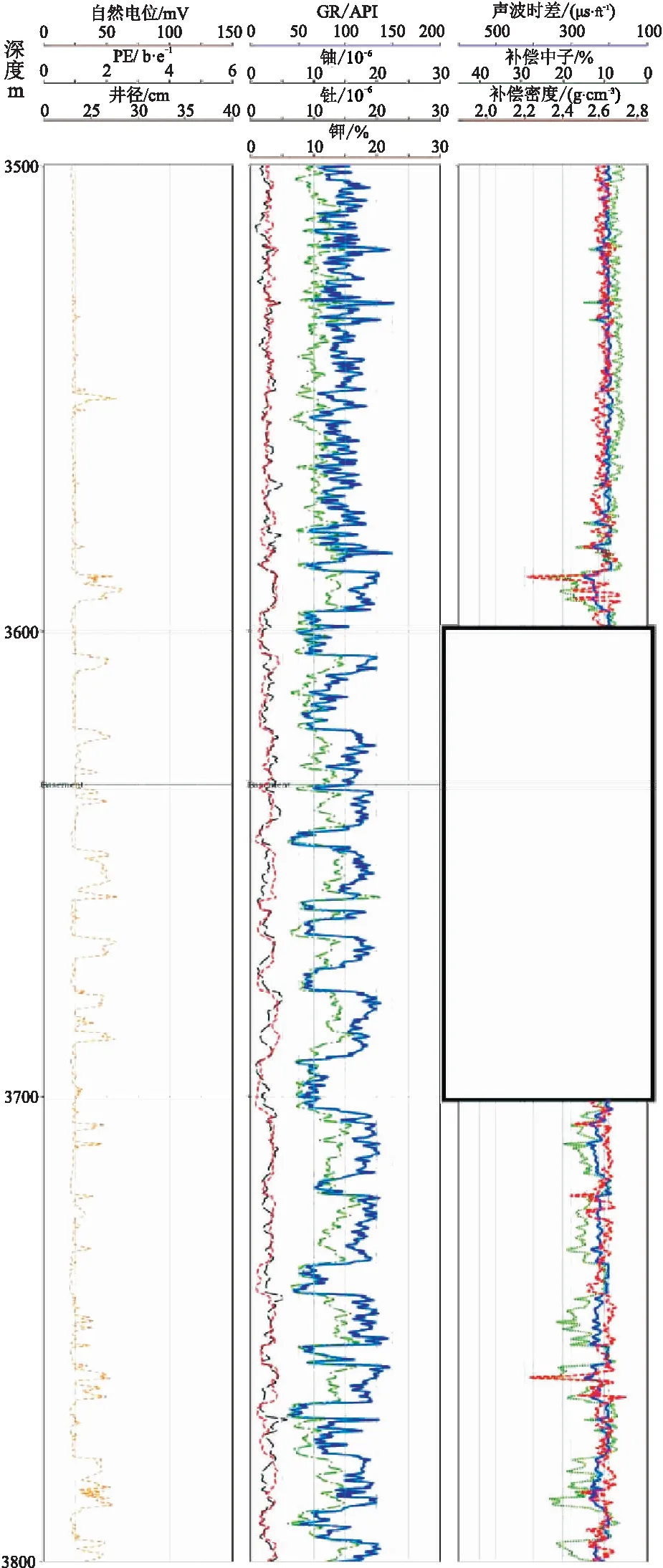
圖6 測井曲線缺失圖

本次實驗中，數據的采樣間隔為0.125m。從地層角度而言，不同深度地層之間相互可產生影響的深度范圍可高達30m，甚至50m。因此，在測井問題中，每個數據點周圍相互有影響的范圍包含的數據點可多達240～400個。因此，網絡模型中每個訓練樣本的序列長度設置為240。最終制作的訓練集一共有20000組訓練數據，每組數據的序列長度為240，用于補全3300～3800m深度區間缺失的測井數據。模型第一級輸入變量為CAL、SP，輸出為AC；第二級輸入變量為CAL、SP、AC，輸出為GR。

2.2 模型評估指標

CBi-LSTM網絡模型屬于回歸模型的一種，采用均方誤差(MSE)、均方根誤差(RMSE)及平均絕對誤差(MAE)作為模型的評估標準。MSE是指參數估計值與參數真實值之差點期望值，可用于評價數據點變化程度，MSE值越小，則模型預測結果越精確。RMSE用于衡量數據的波動性，RMSE值越小，則模型的泛化能力和穩定性就越強。MAE是計算每一個樣本的預測值與真實值的差的絕對值，然后求和再取平均值。用于評估預測結果與真實數據集的接近程度，其值越小說明擬合效果越好。計算公式如下

(17)

(18)

(19)

2.3 測井曲線相關性分析

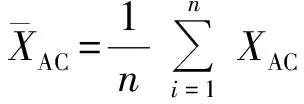
r(XAC,XGR)=

(20)

式中：n為每列的長度；r(XAC，XGR)為曲線XAC與XGR的相關系數，范圍是-1～1，其中1表示完全正相關，-1表示完全負相關，0表示兩屬性無關。

圖7為19條測井曲線之間的相關系數計算結果。從該圖可見：對AC影響較大的有CAL、GR、SP等，且相關系數大于0.5；對GR影響較大的有AC、CAL、SP等。

圖7 測井曲線相關度熱力圖

對于非地層因素CAL，在實際鉆井過程中，CAL會因為地層地質的變化發生形變：砂巖質地堅硬，在鉆井鉆頭經過后由于彈性形變會恢復原來形狀，造成井徑縮小(縮徑)；泥巖質地疏松，會發生井壁垮塌并造成井徑擴大(擴徑)。因此，井徑是判斷地下巖石巖性的重要參數之一。

所以，在地層數據發生變化時，采集到的井徑數據會由于地層地質數據的變化而變化。因此，把CAL作為輔助因素與地層數據進行合并，作為新的數據進行測井實驗。

3 實驗對比分析

3.1 模型重構結果分析

為了對比每一種算法重構測井曲線的能力，分別建立了基于LSTM、Bi-LSTM及改進的CBi-LSTM網絡的重構測井曲線重構模型。對訓練數據做歸一化處理并采用了批訓練方法。批尺寸設置為200，即每次選取200組訓練數據。訓練樣本長度均為240。為充分驗證每一種模型對測井曲線缺失部分重構的能力，分別對每種模型進行4次實驗，每次實驗任選1口井進行測試。

為分析LSTM、Bi-LSTM及CBi-LSTM網絡生成的人工測井曲線的效果，對4口井中預測結果最好的A1井的人工曲線進行繪制(圖8)。

觀察三種方法得到的缺失AC曲線和GR曲線的重構結果(圖8)，可見在A1井3300～3460m深度范圍(圖8上)，隨著模型的不斷改進，AC擬合曲線(藍線)與參照曲線(紅線)之間的誤差逐漸變小，兩條曲線的走勢基本吻合。接著觀察A1井3600～3800m范圍的GR曲線(圖8下)，對比可知，在3600～3650m區間，紅線呈現階躍式變化。常規LSTM網絡及Bi-LSTM網絡在3600～3650m區間都無法準確預測目標曲線的趨勢變化，而所提CBi-LSTM網絡模型卻能準確地擬合出目標曲線的變化趨勢。

圖8 基于LSTM(左)、Bi-LSTM(中)和CBi-LSTM(右)網絡生成的A1井的聲波時差(上)、自然伽馬(下)測井曲線

通過分析圖8中測井曲線重構結果，可知本文的CBi-LSTM網絡能綜合分析預測點前的數據和預測點輸入的影響，彌補了LSTM網絡及Bi-LSTM網絡在進行測井曲線重構過程中存在的不足，準確預測出目標曲線的趨勢性變化。因此，本文的CBi-LSTM網絡對于測井曲線這種序列數據具有更好的重構能力。

3.2 模型結果量化分析

為了量化評價LSTM、Bi-LSTM及本文的CBi-LSTM三種模型重構測井曲線的能力，針對蘇里格氣田4口直井采用此三種模型進行對比實驗。基于皮爾遜算法對測井曲線進行特征分析，利用與AC和GR相關性高的測井曲線分別對AC和GR進行數據重構，并對重構結果進行量化評估。

表1展示了三種方法測井曲線的估計值的均方誤差、均方根誤差及絕對值差。由表1可知，首先利用LSTM網絡重構測井曲線并取得較好效果，但還存在上述兩點缺陷。因此引入Bi-LSTM網絡構建出考慮測井曲線的變化趨勢即上下數據相關關系的數據重構模型，并將實驗結果量化。通過對比表1中的數據可見，Bi-LSTM網絡整個模型魯棒性和泛化能力比LSTM網絡更穩定。但針對第二個問題，仍然無法解決。因此，為了進一步提高模型的靈活性及適應性，將串級系統與Bi-LSTM網絡相結合，利用本文的CBi-LSTM網絡對測井曲線進行了重構，通過對比表1量化數據可知，本文的網絡模型取得了更好的成績。不僅如此，整個模型的魯棒性和泛化能力不僅得到了提高，而且模型在曲線重構的過程中，具有了動態優化及自適應動態重構測井曲線的能力。

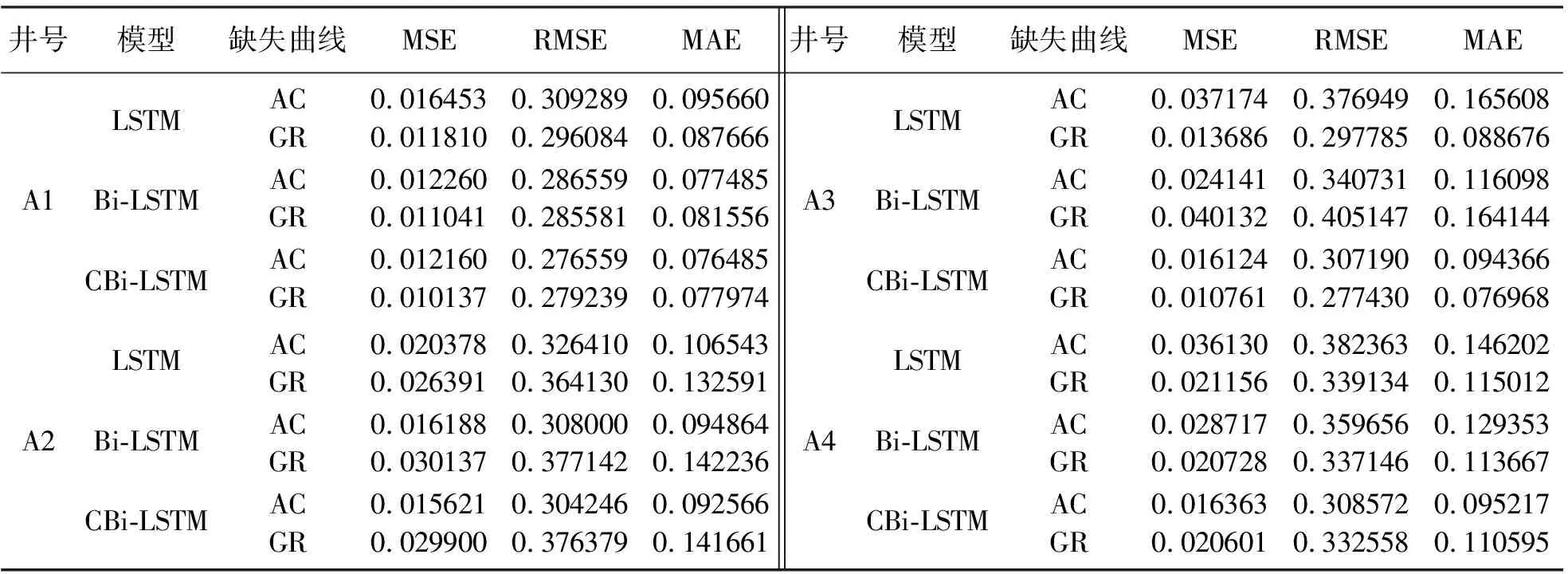
表1 不同模型生成人工測井曲線模型數據評估

4 結束語

本文提出一種基于改進CBi-LSTM神經網絡的測井數據重構方法。將Bi-LSTM與串級系統相結合，通過利用Bi-LSTM網絡提取缺失數據前后序列數據的關鍵特征信息對缺失數據點進行預測，然后將獲得的估計值與已知測井曲線合并為新的輸入，采用串級更新策略完成對缺失數據塊的重構。充分考慮當前井測井曲線之間相關性，提高了模型的適應性及靈活性。針對蘇里格氣田4口井測井數據進行處理重構，并與LSTM和Bi-LSTM模型做對比分析，結果表明改進的CBi-LSTM模型對測井數據具有更高重構精度。