一階速度—脹縮—旋轉彈性波方程交錯網格數值模擬

王 輝 何兵壽* 邵祥奇

(①中國海洋大學海底科學與探測技術教育部重點實驗室，山東青島 266100；②青島海洋科學與技術國家實驗室海洋礦產資源評價與探測技術功能實驗室，山東青島 266100；③山東省煙臺市自然資源和規(guī)劃局，山東煙臺 264003)

0 引言

彈性波正演是研究縱橫波傳播規(guī)律的重要工具之一，在多波地震的資料采集、處理、解釋和反演等領域發(fā)揮著重要作用。彈性波方程及其模擬算法是多年來業(yè)界廣泛關注的熱點。

近年來，在彈性波方程的有限差分數值模擬領域開展了大量的研究工作，取得了許多成果，包括彈性波偏微分方程組中空間偏導數的高階差分格式[1-5]、時間偏導數的高階差分格式[6-9]、各種差分格式的穩(wěn)定性條件[10-14]、數值頻散的壓制方法[15-19]、邊界條件[20-23]以及計算效率提升方法[24-25]等。這些成果對于推動多波地震技術的發(fā)展具有重要意義。但總體而言，現有的彈性波正演技術仍存在諸多不足。①模擬精度與效率很難兼顧。小網格、高階差分格式可以提高模擬精度，但意味著計算量的指數級增加，導致模擬效率降低。雖然近似解析離散[26-27]等方法可以適應大網格的差分計算，但其計算量仍遠大于預期。②基于長方體網格的空間剖分方法無法準確擬合復雜界面的形態(tài)，導致模擬結果中出現大量繞射波。近年出現的不規(guī)則網格技術[4，28-29]雖然緩解了這一問題，但距離根本解決還為時尚早；③現有算法能準確模擬彈性波的傳播過程，模擬得到的三個分量均同時包含縱波和橫波[30]，必須借助額外的波場解耦算子[31-32]才能得到純縱波和純橫波的模擬結果，即模擬的縱、橫波記錄和快照同時受制于差分算法的精度和解耦算子的精度，增加了誤差來源[33-34]。

為解決上述第三個問題，本文通過對一階速度—脹縮—旋轉彈性波方程的差分離散實現彈性波的模擬。首先推導了一階速度—脹縮—旋轉彈性波方程在三維交錯網格空間中的高階有限差分格式，給出了相應的穩(wěn)定性條件；然后導出了適應該方程的PML吸收邊界條件，在此基礎上實現了一階速度—脹縮—旋轉彈性波方程的正演模擬。本文的彈性波模擬方法的優(yōu)勢在于，不僅可以得到x、y、z三分量地震記錄，而且無需顯式地進行縱、橫波解耦就可以得到橫波振動速度矢量和縱波振動速度矢量，實現了縱、橫波的保幅解耦。同時，數值求解該方程還可以直接得到各質點的體應變和旋轉矢量，為分析不同速度模型條件下縱、橫波的傳播規(guī)律提供更詳細的信息。

1 速度—脹縮—旋轉彈性波方程

各向同性介質中的三維一階速度—脹縮—旋轉彈性波方程[35]為

(1)

式中：v=(vx，vy，vz)為質點振動速度矢量；vS=(vSx，vSy，vSz)為質點的橫波振動速度矢量；vP=(vPx，vPy，vPz)為質點的縱波振動速度矢量；cP、cS分別為縱、橫波傳播速度；θ為體應變；ω=(ωx，ωy，ωz)為旋轉矢量。

式(1)不僅顯式地包含了常規(guī)彈性波方程中的質點總振動速度矢量，而且包含了由脹縮運動和剪切運動引起的質點振動速度矢量，同時還顯式包含了θ和ω，因此利用該方程進行彈性波正演模擬不僅可以得到x、y、z三分量地震記錄，而且無需顯式地進行縱、橫波解耦就可以得到縱波振動速度矢量和橫波振動速度矢量。同時，數值求解該方程還可以直接得到各質點的體應變和旋轉矢量，體應變一般只與縱波有關，旋轉矢量一般只與橫波有關，這為分析不同速度模型條件下縱、橫波的傳播規(guī)律提供了更詳細的信息。

此外，由于目前的多波地震采集基本都采用縱波源激發(fā)，式(1)顯然十分便于解決彈性波正演中的縱波源設置問題，模擬時只需將震源函數加載到體應變θ上即可實現縱波源激發(fā)。而采用傳統的一階速度—應力方程進行彈性波模擬時，縱波源必須加載到三個正應力分量上[9，13]，但縱波源的總能量按照什么樣的比例分配到三個正應力分量上，目前并沒有一個公認的結論。

2 交錯網格數值模擬方法

2.1 交錯網格高階差分格式

三維情況下，在圖1所示的交錯網格空間[3-4]中求解式(1)，其中各波場分量在交錯網格空間中的配置由表1給出。

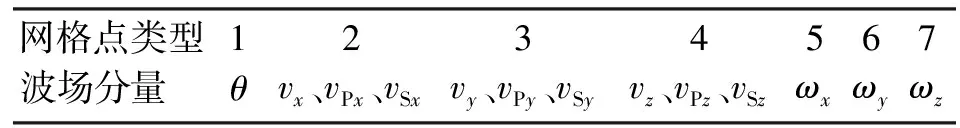
表1 各波場分量在交錯網格中的分布

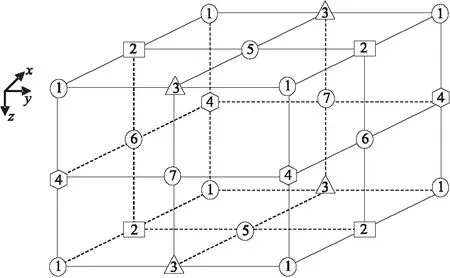
圖1 三維交錯網格示意圖

采用高階有限差分算法[6，8-9]對式(1)進行差分離散，可得到三維一階速度—脹縮—旋轉彈性波方程正演模擬的時間2階、空間2N階有限差分格式。以θ分量為例，可表示為

--------------------

(2)

式中：Δt為時間延拓步長；Δx、Δy、Δz分別為直角坐標系中x、y、z方向上的網格剖分間距；n為時間離散序號；i、j、k分別代表x、y、z方向上的離散網格點序號；Cm為2N階精度的交錯網格差分系數，

其計算公式為[4，9，13]

(3)

表2為由式(3)得到的12階以內各階差分的系數，一般來說，差分階數越高，模擬結果的精度越高。圖2為均勻介質模型的空間2階和12階有限差分模擬的vx分量快照，其中縱、橫波速度分別為2800、1620m/s，空間三個方向的剖分間距均為5m，時間步長為0.5ms，縱波源是主頻為30Hz的Ricker子波，位于(500m，500m，500m)處。顯然，12階精度的差分格式能獲得更精確的模擬結果。雖然差分階數越高模擬精度越高[5]，但差分階數的提高也意味著計算量的迅速增大。數值實驗表明，當差分階數增高到一定程度后，繼續(xù)增高對模擬精度的提升十分有限。本文綜合考慮模擬精度和計算效率兩個因素后，采用12階精度的差分格式實現式(1)的數值模擬。

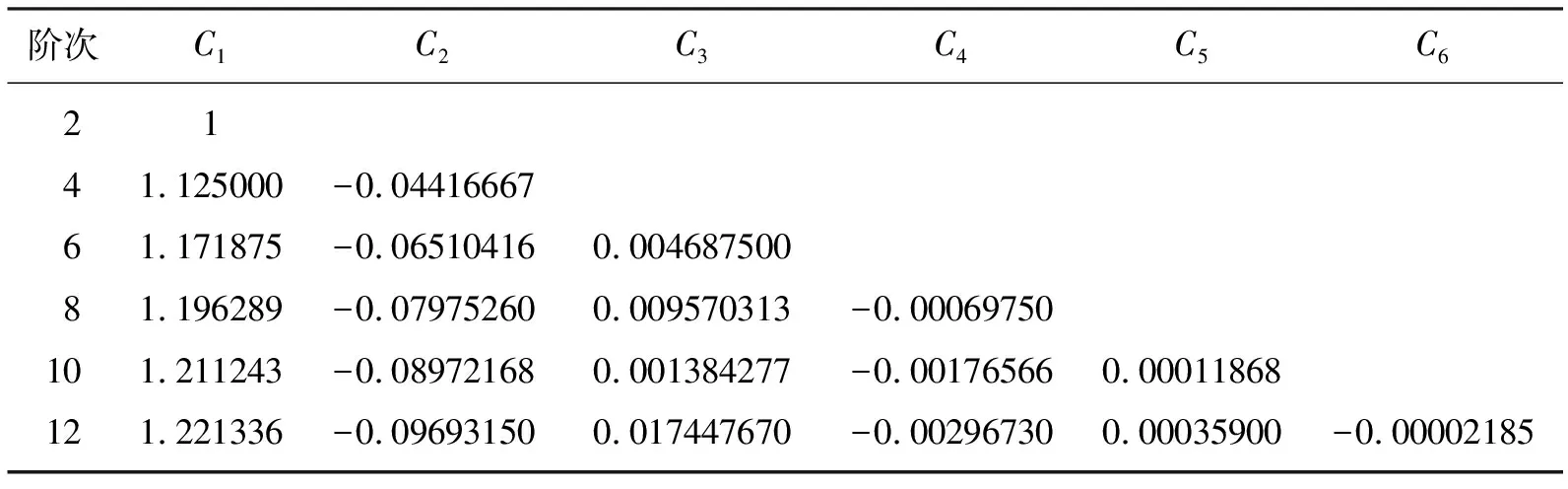
表2 交錯網格不同階次有限差分系數

圖2 均勻模型2階(a)和12階(b)有限差分模擬的波場快照

2.2 穩(wěn)定性條件

采用與文獻[13，36]相同的推導方法可得式(2)的穩(wěn)定性條件為

(4)

式中vmax為模型中的最大速度。

2.3 PML吸收邊界條件

本文引入地震波方程正演領域常用的PML邊界條件[21-23]吸收入射到模型邊界的外行波。采用圖3所示的鑲邊方案在模型周邊鑲嵌PML吸收層，圖3中區(qū)域Ⅰ為8個角點區(qū)，區(qū)域Ⅱ為12條棱邊區(qū)，區(qū)域Ⅲ為剩余的6個面。

圖3 三維空間PML鑲邊方案示意圖

以θ分量為例，在鑲邊區(qū)域將θ分量分解為θx、θy和θz三個分量，分別計算各分量，再求和得到鑲邊區(qū)域的θ分量，即

(5)

式中dx、dy、dz分別為x、y、z三個方向上的衰減因子，其計算公式為[9，22]

(6)

式中：V為波速，一般取縱波速度cP；R為理論邊界反射系數，一般取經驗值0.0001[9]；δ為PML鑲邊層厚度；hx、hy、hz分別為鑲邊層中的各網格點與有效計算區(qū)域邊界的最短距離。

同樣在交錯網格空間中對式(5)進行差分離散，可得到式(5)的高階有限差分格式

(7)

同理可得出其他波場分量的PML吸收邊界及其高階差分格式。對比均勻模型加與不加PML吸收邊界的波場快照(圖4)可見，本文的PML邊界條件幾乎能完全吸收入射到截斷邊界的外行波。

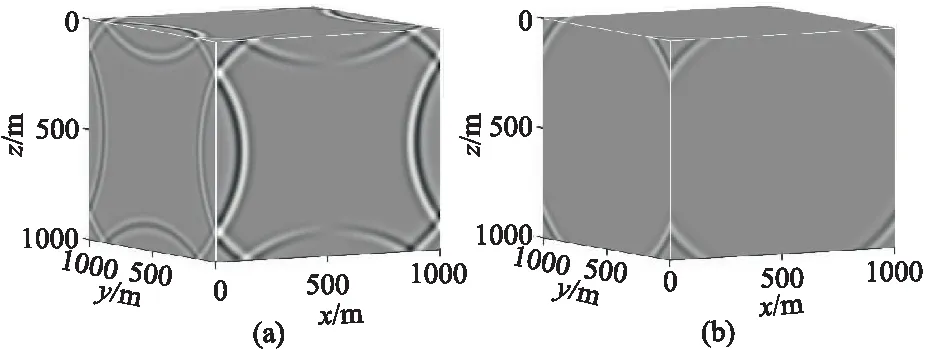
圖4 不加(a)與加(b)PML吸收邊界的vx分量快照對比

3 模擬快照分析

對一個簡單的兩層水平層狀介質模型分別采用一階速度—應力彈性波方程[9]和一階速度—脹縮—旋轉彈性波方程[32]進行數值模擬，利用模擬快照分析兩個方程的聯系和區(qū)別。模型尺寸為1000m×600m×1000m，上層縱、橫波速度分別為2250、1300m/s，下層縱、橫波速度分別為2900、1676m/s，界面埋深為350m，空間網格尺寸為5m×5m×5m，時間采樣間隔為0.5ms。兩個方程均采用空間12階精度的有限差分算法進行模擬。經驗證，以上模擬參數同時滿足兩個方程的穩(wěn)定性條件。均采用主頻為30Hz的Ricker子波作為縱波激發(fā)源，炮點位于(500m，300m，0)處。對一階速度—應力方程模擬時，縱波源加載到三個正應力分量上，而對一階速度—脹縮—旋轉方程進行模擬時，由于該方程沒有顯式包含應力分量，故將縱波源加載到體應變θ上。兩種算法模擬所需的計算量如表3所示(一階速度—應力方程的模擬過程包含了基于散度和旋度算子的縱橫波分離運算)，顯然，相同精度條件下，本文算法的運算量低于一階速度—應力彈性波方程數值模擬的運算量。

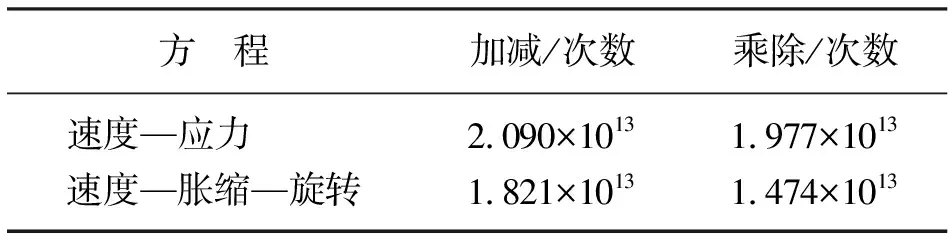
表3 兩種方法計算量對比

圖5為0.35s時刻兩種方程模擬的vx、vy、vz分量快照，是野外采集中可以直接用速度檢波器接收并記錄的信息。由于波的傳播方向并非與坐標軸完全平行，因此三個分量中均同時包含縱波與橫波。顯然，由兩個方程得到的質點的振動速度是完全一致的(因為二者的物理意義本就是相同的)。這說明，如果以得到三分量炮記錄為正演目標，則式(1)可以獲得與一階速度—應力方程完全相同的結果。

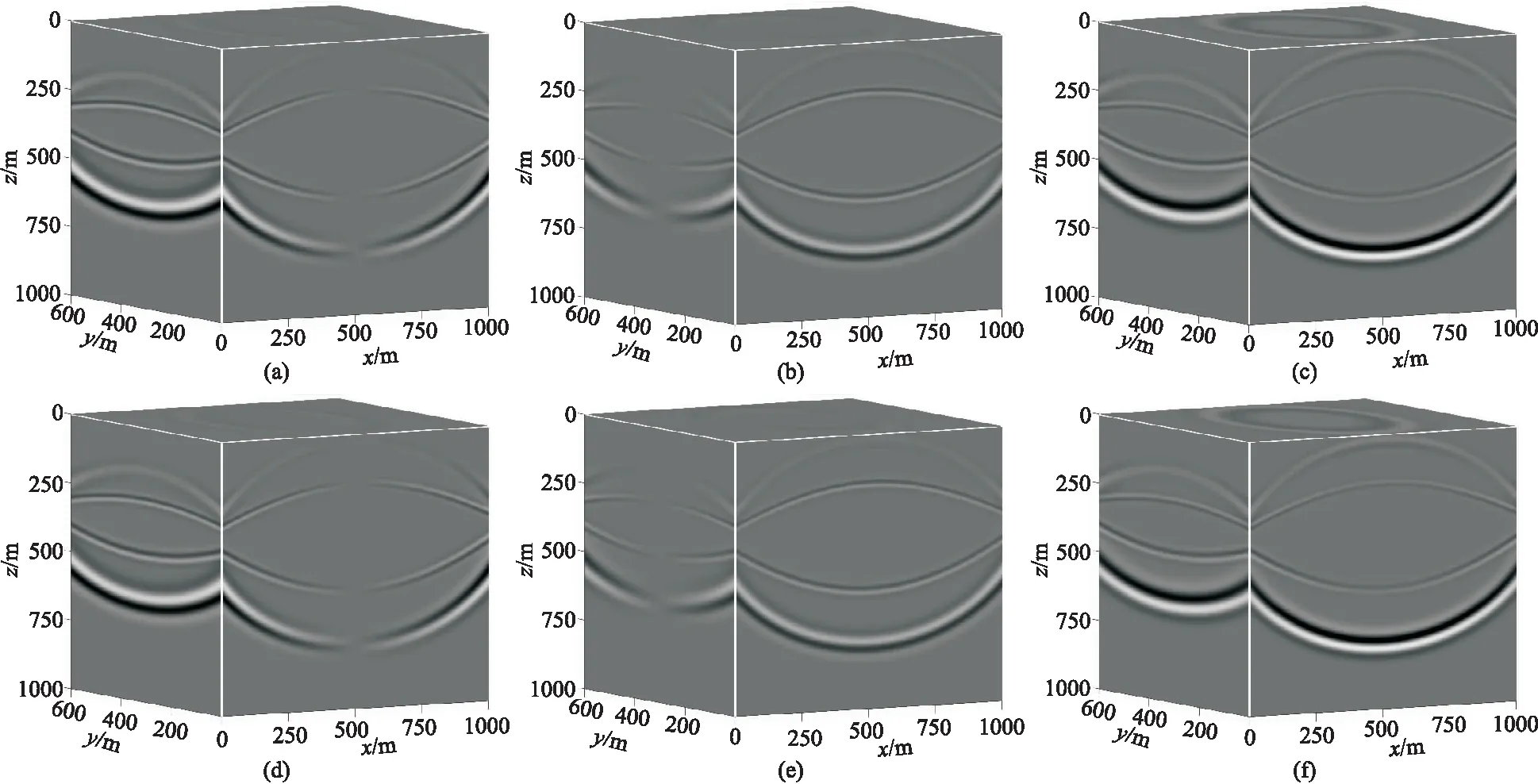
圖5 水平層狀模型兩種方程模擬的波前快照對比(一)

圖6a～圖6d為式(1)正演得到的ω的三分量快照和θ的快照。依據式(1)，θ和ω對時間的偏導數分別對應v的散度和旋度，分別指示縱波和橫波。圖6e～圖6g為直接對圖5d～圖5f求旋度和散度的結果，它們幾乎與ω和θ的快照完全相同，表明θ和ω能代替一階速度—應力彈性波方程中質點振動速度的散度和旋度。需要說明的是，雖然業(yè)界常通過直接求取v的散度和旋度分離縱、橫波，但這種方法得到的結果只在波形上與真實的縱、橫波相似，卻沒有明確的物理意義，因為只有當Helmholtz分解的對象是位移矢量時，分離結果才有明確的物理意義，因此圖6a～圖6d具有明確的物理意義，而圖6e～圖6g則不然。此外，對比圖6與圖5還可以看出，上述兩種方法得到的橫波的x分量和y分量與分離前混合波場中橫波的x分量和y分量存在90°的相位差，其極性反轉位置沒有與分離前混合波場中的各分量對應。而分離后的橫波z分量為零，這顯然與實際情況不符。這說明基于散度和旋度算子的波場分離方法不能實現縱、橫波的保幅分離。圖6c和圖6g為零的原因是：在進行旋度運算時，ωz是vy在x方向的偏導數與vx在y方向的偏導數之差，由于本算例所用的模型在z方向上水平分層，vy在x方向的偏導與vx在y方向的偏導相等，故旋度的z分量為零。

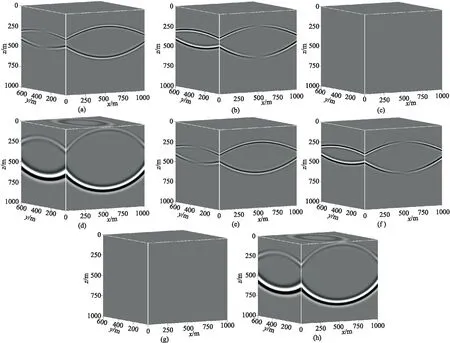
圖6 水平層狀模型兩種方程模擬的波前快照對比(二)

圖7為在式(1)方程的正演直接得到的純vP和純vS的三分量快照，與圖5對比可見，圖7不僅實現了縱、橫波的完全分離，并且分離后各分量的縱、橫波的極性與混合波場中的極性完全對應，相位也保持一致。同時，依據式(1)，由于混合波場v是兩個矢量波場vS和vP的簡單相加，因此利用式(1)得到的縱、橫波分離結果一定是保幅的。圖8為水平位置(250m，0)處vx、vPx、vSx分量垂向波形對比，證明了一階速度—脹縮—旋轉彈性波方程能夠實現縱橫波的保幅分離。與現有的縱、橫波保幅分離算法相比，本文算法的優(yōu)勢在于：一階速度—脹縮—旋轉彈性波方程無需任何額外計算即可實現縱、橫波的完全分離，分離精度只與模擬算法的精度有關，而現有的縱、橫波保幅分離算法的精度同時受制于模擬算法的精度和解耦算子的精度。

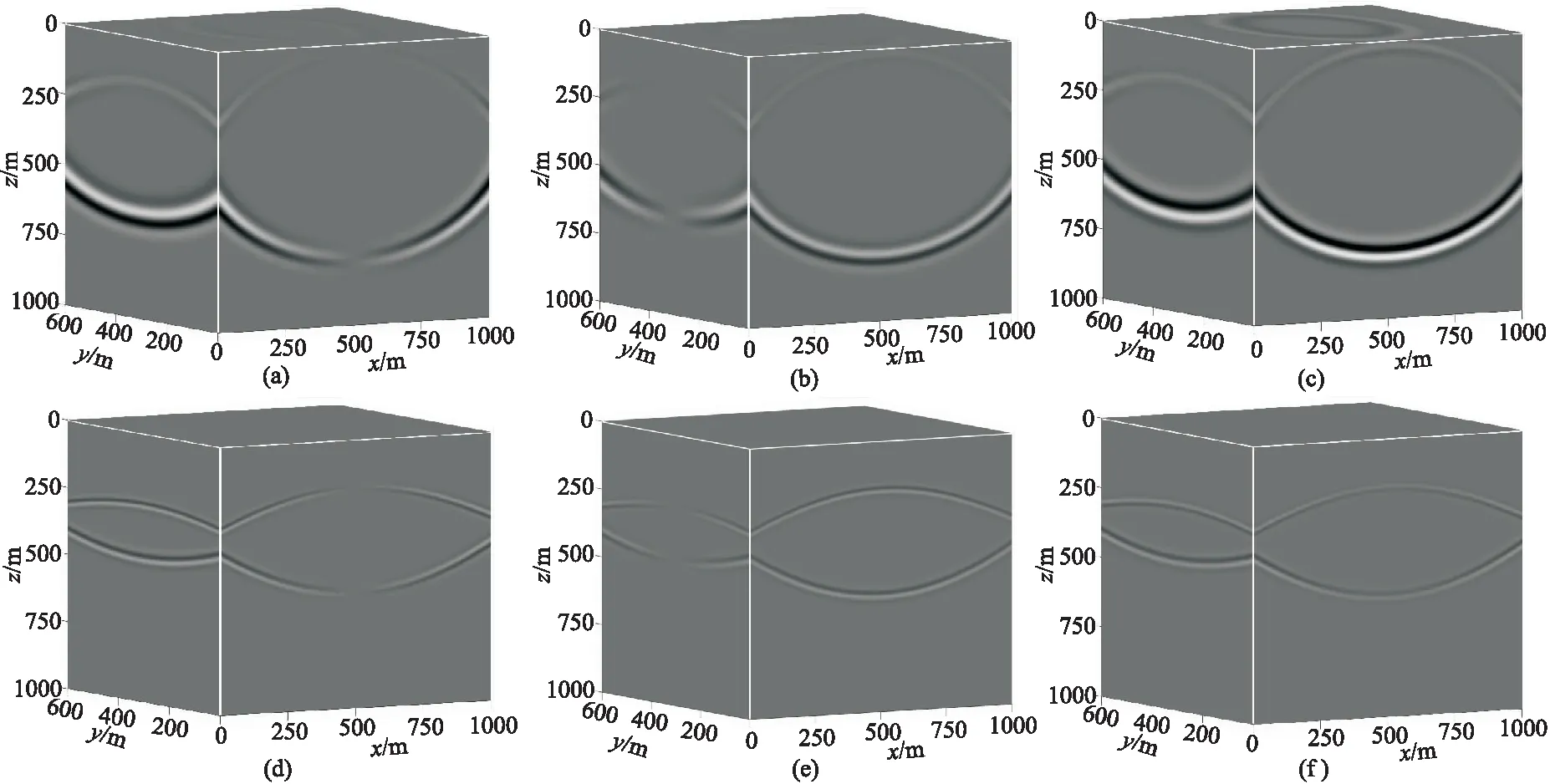
圖7 水平層狀模型速度—脹縮—旋轉彈性波方程模擬的純vP、純vS各分量快照

圖8 本文方法模擬的vx、vPx、vSx分量垂向波形對比

4 數值算例

用SEG/EAGE鹽丘模型檢驗本文模擬算法的正確性，并進一步分析一階速度—脹縮—旋轉方程在彈性波模擬與應用方面的優(yōu)勢。模型尺寸為1000m×1000m×1000m，縱、橫波速度模型如圖9所示，空間網格尺寸為5m×5m×5m，時間步長為0.35ms，模擬參數滿足穩(wěn)定性條件。縱波震源是主頻為30Hz的Ricker子波，炮點坐標為(500m，500m，0)。地震記錄長度為1.05s，8條多分量接收線位于地表，間距為125m，第1、第8條分別位于y=0、y=875m處，每條線200道，道間距為5m，單炮共有1600道。

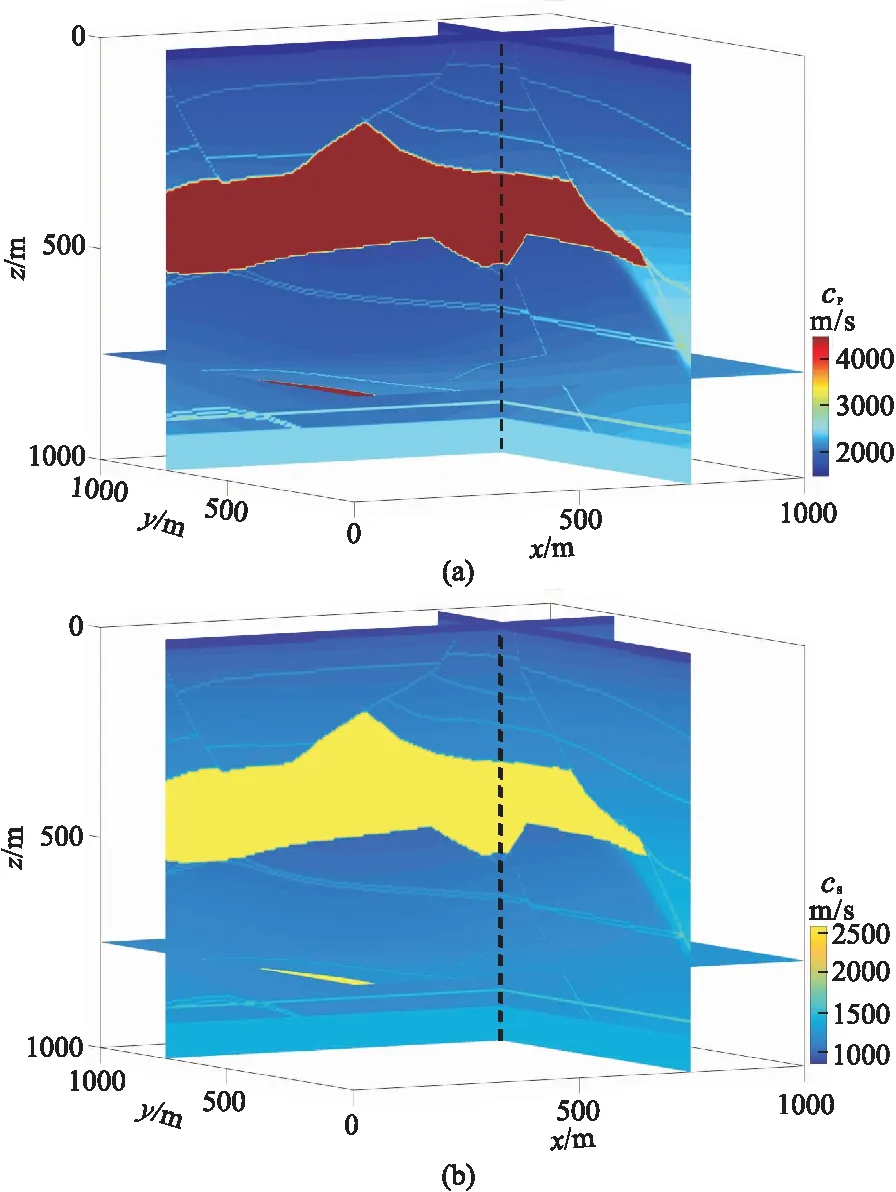
圖9 三維鹽丘模型

圖10、圖11為正演得到的各分量單炮記錄。由于該模型包含了斷層、凹陷、隆起、傾斜界面和水平界面，使得彈性波的傳播過程極為復雜且混合波場中縱波與橫波耦合在一起，難以區(qū)分，不便于分析縱、橫波的傳播過程，也不便于評價觀測系統的合理性。而一階速度—脹縮—旋轉方程可以在波場延拓中直接獲得vS和vP的各個分量，使混合在一起的波場得到分離，為分別研究反射縱波或轉換橫波的傳播過程和機理提供了更準確的信息。同時，上述結果也說明一階速度—脹縮—旋轉彈性波方程還有利于在延拓過程中直接求取純縱波或純橫波的某些屬性，如縱波的傳播方向、橫波的傳播方向及其極化方向等，而這些屬性信息又往往是偏移和反演等環(huán)節(jié)的關鍵信息。

圖10 部分三維鹽丘模型本文方法模擬的混合波場地震記錄

圖11 部分三維鹽丘模型本文方法模擬的純波地震記錄

5 結論與討論

本文給出了三維各向同性介質中一階速度—脹縮—旋轉彈性波方程的高階有限差分格式及其穩(wěn)定性條件，以此為基礎實現了該方程的數值模擬，并利用模型模擬結果詳細分析了該方程的優(yōu)勢，得出如下結論。

(1)本文算法能實現一階速度—脹縮—旋轉彈性波方程的高精度數值模擬。

(2)除能獲得常規(guī)彈性波模擬中的三分量合成記錄和波場快照外，一階速度—脹縮—旋轉彈性波方程還能夠在不增加任何額外運算的前提下直接實現彈性波的保幅解耦。解耦結果是一個縱波速度矢量和一個橫波速度矢量，除了便于分析縱、橫波在各個方向的振動情況外，還特別有利于求取純縱波或純橫波的傳播方向和極化方向等屬性信息。同時，由于解耦結果是兩個矢量，避免了彈性波逆時偏移中進行互相關成像時矢量和標量無法相關的難題。

(3)對一階速度—脹縮—旋轉彈性波方程進行數值模擬還可以直接得到一個體應變θ和旋轉矢量ω，其物理意義與常規(guī)彈性波方程中位移矢量的散度和旋度算子的物理意義相同。θ與ω雖然與特定模型條件下的縱橫波傳播過程有關，但不能準確描述縱、橫波傳播過程。

(4)本文模擬得到的vS和vP都是矢量，而事實上，各向同性介質中的縱波是標量，雖然vP可以準確描述由脹縮運動導致的質點振動在各個方向的投影情況，但由于業(yè)界習慣于將縱波當成一個獨立標量處理和分析，因此將vP合成為一個標量更易為業(yè)界接受，現有的矢量波場的標量化處理技術完全可以解決這一問題。