徑向安裝測量軸向位移傳感器線圈電感的解析計算

崔 猛

（中車株洲電機有限公司，湖南 株洲 412000）

引言

在磁懸浮電機中，轉子軸向位移通常采用正對轉子軸端面安裝的電渦流傳感器從轉子軸向方向檢測，對于安裝空間受限的場合，徑向安裝測量軸向位移是一種有效的解決方式，同時有利于優化轉子結構，獲得更好的轉子動力學性能[1-3]。

文獻[4]最早提到了法國S2M 公司將磁軸承軸向和徑向位移傳感器安裝在同一個環形傳感器支架上，徑向傳感器和軸向位移傳感器并排安裝在支架上，軸向傳感器通過徑向安裝測量軸向位移的方法，文獻[1-4]在此基礎上開展了基于電渦流傳感器的徑向安裝測量軸向位移的相關研究。文獻[1]和文獻[3]研究了被測面為臺階測量軸向位移，兩個對稱布置的傳感器測量軸向位移，文獻[2]研究了被測面為45°斜面測量軸向位移，文獻[4]研究了被測面為鋼鋁交接面、鋁和空氣交接面測量軸向位移，上述研究結果均表明徑向安裝可以準確測量軸向位移。文獻[5-8]開展了電感式位移在磁軸承中的應用研究，研究結果表明在電感式位移傳感器抗干擾能更強，在小測量范圍內具有更高的靈敏度和線性度。采用文獻[4]中提到的傳感器布置結構的電感式位移傳感器已經被S2M、MECOS 等磁軸承企業開始大批量使用，文獻[9]中對電感式位移傳感器徑向安裝測量軸向位移的結構和工作原理進行了詳細說明。

在徑向安裝測量軸向位移的電感式位移傳感器的設計中，常規電感解析計算式已經不再適用，需要在有限元三維運動場中進行仿真計算，這樣需要花費大量的仿真資源和時間。采用文獻[10]中所述的磁場分割法，本文推導出了針對這種結構的線圈電感的解析計算式，可以快速和準確的計算出電感式位移傳感器在不同位移下的線圈電感值。

1 計算模型

電感式位移傳感器徑向安裝測量軸向位移的布局結構見圖1，Z 軸為轉子回轉中心，XY 平面位于被測體臺階面上，探頭在Y 方向上對稱安裝，d 為探頭與被測面額定測量間隙，h 為階梯的高度，當傳感器與轉子軸向方向發生相對移動時，氣隙磁阻發生變化，電感隨位移在一定范圍內呈線性變化，從而測量出軸向位移。

考慮了邊緣磁路的常規電感計算公式如式（1）所示，K 為邊緣修正系數，A 為磁極面積，N 為勵磁線圈匝數。式（1）適用于磁極面為規則幾何形狀，氣隙磁通均勻分布和邊緣磁通規則分布的情況。

為了準確掌握圖1 中所示傳感器結構的磁極間氣隙及邊緣氣隙磁通的分布情況，我們在有限元三維場中進行仿真計算，根據仿真結果的磁通分布規律，首先采用磁場分割法將其劃分為多個區域，如圖2 所示，然后采用數學解析法分別計算各區域磁導，通過并聯關系求得總磁導，如式（2）所示，其中未標注區域的磁通路徑復雜且占比很小，可以忽略。

2 磁導計算

根據磁場分割法中磁通管的概念，將氣隙磁通分布規律相同的區域劃分若干個微小的磁通管，單個磁通管內的磁勢相等，那么在式（3）的基礎上可以進一步推導出氣隙磁導的計算如式（5）所示。

式（5）中，dAi為單個微小磁通管的磁極面積。

2.1 區域Ⅰ

2.2 區域Ⅱ

2.3 區域Ⅲ

2.4 區域Ⅳ

2.5 區域Ⅴ

從圖2 中可知，區域Ⅴ由四分之一空心圓柱體、一個長方體和四分之一圓柱體組成，磁通路徑

2.6 區域Ⅵ

2.7 區域Ⅶ

3 樣機驗證

樣機主要技術參數見表1，樣機試驗測試裝置見圖3。

樣機計算結果、仿真結果和實測結果見表1。

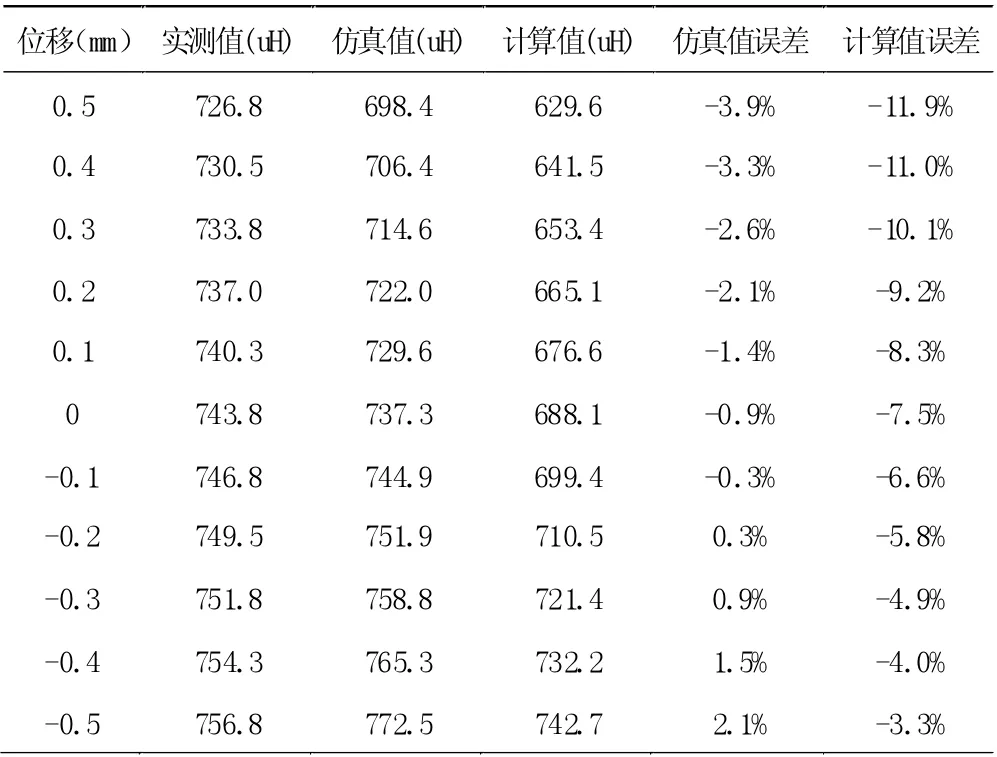
表1 結果與誤差分析

從表1 中可以看出，與實測值相比，仿真值和解析計算值在傳感器的線性工作區間內均存在誤差，仿真誤差相對更小。本文所述的解析計算比實測值整體偏小的原因是，一方面忽略為部分占比很小，磁通路徑復雜的區域，另一方面是采用圓弧線和直線對磁通路徑進行擬合不夠準確，特別是探頭向正方向移動時實際磁通路徑與擬合路徑差異變大，導致誤差變化率隨著探頭正向位移的增加不斷變大。

4 結論

本文根據徑向安裝測量軸向位移傳感器的磁場分布特點，采用磁場分割法將劃分為多個區域，建立了軸向位移傳感器電感值在不同位移時解析計算公式。解析計算的電感值誤差雖然略大于有限元計算誤差，但是其可以滿足傳感器的設計要求，同時可以大幅提升傳感器線圈電感的計算效率。