無窮時滯測度泛函微分方程的Lyapunov逆定理①

李寶麟， 王雪蓮

西北師范大學 數學與統計學院，蘭州 730070

Kurzweil J[1-2]于1957年建立了廣義常微分方程理論.文獻[2]建立了測度微分方程與廣義常微分方程的等價關系.文獻[3]給出了無窮時滯測度泛函微分方程的穩定性結果，證明了無窮時滯測度泛函微分方程在某些條件下等價于廣義常微分方程.文獻[4]建立了廣義常微分方程的Lyapunov穩定性定理.文獻[5]定義了廣義常微分方程的正則穩定性，建立了測度泛函微分方程的Lyapunov定理.文獻[6]提出了具有無窮時滯的經典泛函微分方程或脈沖泛函微分方程的相空間.文獻[7]定義了廣義常微分方程的正則穩定性和Lyapunov泛函，證明了廣義常微分方程關于正則穩定性的Lyapunov逆定理；定義了測度泛函微分方程的積分穩定性，并建立了測度泛函微分方程關于積分穩定性的Lyapunov逆定理.文獻[8]研究了測度微分方程和時間尺度上動力方程的Lyapunov穩定性.文獻[9]建立了測度泛函微分方程和廣義常微分方程之間的等價關系.文獻[10]建立了無窮時滯測度泛函微分方程的周期和非周期平均化定理.文獻[11]利用廣義常微分方程建立了一類滯后泛函微分方程

(1)

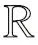
受到以上工作的啟發，本文將在文獻[7]的基礎上，利用無窮時滯測度泛函微分方程在一定條件下可以轉化為廣義常微分方程的特點(文獻[3]中給出了詳細的證明)，討論無窮時滯測度泛函微分方程

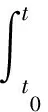
(2)

(H1)H0是完備的；

(H2)如果y∈H0，t<0，則yt∈H0；

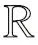
1 預備知識

本節將簡要介紹Kurzweil積分、廣義常微分方程、無窮時滯測度泛函微分方程以及Lyapunov泛函的相關概念以及定理.

設s≥t0，x∈O，A(s，x)：={φ∈G([t0，t0+σ]，X)：φ(t0)=0，φ(s)=x，φ在(t0，t0+σ]上是左連續的}.

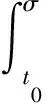
[t0，s]

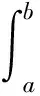
(3)

在區間[a，b]?[t0，t0+σ]上的解，是指對所有的t∈[a，b]，(x(t)，t)∈Ω和對任意的s1，s2∈[a，b]，

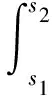
成立.

‖F(x，s2)-F(x，s1)‖≤|h(s2)-h(s1)|

‖F(x，s2)-F(x，s1)-F(y，s2)+F(y，s1)‖≤‖x-y‖|h(s2)-h(s1)|

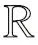
1)Ha是完備的.

2)如果y∈Ha，t≤a，則yt∈H0.

3)如果y∈Ha，t≤a，則‖y(t)‖≤κ1(t-a)‖y‖*.

4)如果σ>0，y∈Ha+σ是支集包含在[a，a+σ]上的函數，則

5)如果y∈Ha+σ，t≤a+σ，則

金融創新從宏觀層面講，就是將金融創新與金融史上的重大歷史變革等同起來，整個金融業的發展史就是一部不斷創新的歷史，金融業的每項重大發展都離不開金融創新。從這個角度看，農業銀行服務“三農”使命的確立，契合了金融創新的理念，“三農”的根本在于農業，農業的根本在于水利，服務水利即是服務“三農”。在這方面《意見》對農業銀行提出了明確要求，“在財務可持續的前提下，中國農業銀行要加強和水利、農業等部門的溝通，及時了解水利項目儲備和安排的特點，積極參與對水利改革發展的金融支持和服務”。

‖yt‖*≤κ3(t-a-σ)‖y‖/

其中存在σ∈[a，b]使得c=‖g(σ)‖，或存在σ∈[a，b)使得c=‖g(σ+)‖.

定義4[5]廣義常微分方程(3)的平凡解x≡0被稱作

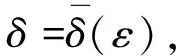
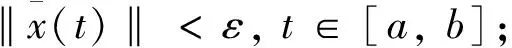
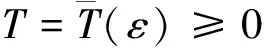
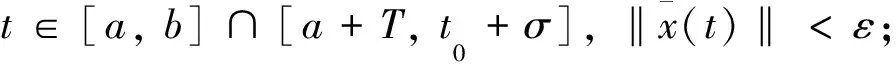
(iii)正則漸近穩定.如果它既是正則穩定又是正則吸引的.

1)對所有s≥t0，V(s，0)=0；

2)對所有y∈O和s≥t0，V(s，y)≥0.

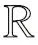
V(t，x)≥b(‖x‖)

成立，則V的右導數關于廣義常微分方程(3)的解是非正的.

引理6[7]對所有s≥t0，y∈O，A(s，y)是閉的.

V(s，y)-V(s，x)≤‖y-x‖

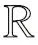
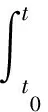
(4)

等價于廣義常微分方程

(5)

對每個x∈O，t∈[t0，t0+σ]，方程(5)的解x和方程(4)的解y之間的關系如下：

2 主要結果

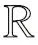
(iii)對每個t≥t0和ψ∈P，

定義6測度泛函微分方程(4)的平凡解y≡0稱作

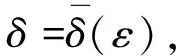
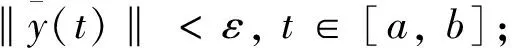
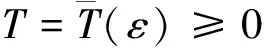
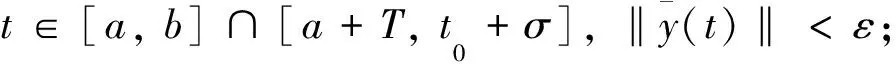
(iii)正則漸近穩定.如果它既是正則穩定又是正則吸引的.

(iv)對所有t∈[t0，t0+σ]，W(t，0)=0；

成立.即函數W的右導數關于測度泛函微分方程(4)的解是非正的.

由于σ0∈(t0，t0+σ]，ε>0，h和yt在(t0，t0+σ]上左連續，存在δ>0使得對每個t∈[σ0-δ，σ0)有

|h(t)-h(σ0)|<ε‖yt(t)-yt(σ0)‖<ε

(6)

下面證明對每個t∈[σ0-δ，σ0)有

|V(t，，xψ)-V(σ0，，xψ)|<ε

設任意t∈[σ0-δ，σ0)，有

由引理8和(6)式有

V(t，xψ)-V(σ0，xψ)≤V(t，xψ)-V(t，yt(t))≤‖xψ-yt(t)‖=‖ψ(σ0)-yt(t)‖<ε

(7)

V(σ0，yt(σ0))-V(t，yt(t))≤0

因此

(8)

由于ψ是初始條件為yt=ψ的測度泛函微分方程(4)的解，

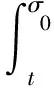
(9)

由引理8有

V(σ0，xψ)-V(σ0，ψ(σ0))≤‖yt(σ0)-xψ‖

(10)

由(8)，(9)和(10)式有

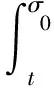
(11)

根據(7)和(11)式，對所有t∈[σ0-δ，σ0)，

|V(σ0，xψ)-V(t，xψ)|<ε

因此，

|W(σ0，ψ)-W(t，ψ)|<ε

下面證明(ii)：存在ε>0和一個序列對(tk，yk)∈[t0，t0+σ]×O，k=1，2，…，使得

ε≤‖yk‖

(12)

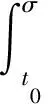
由于φk(t0)=0，Pk(t0)=0，因此，

對σ∈[t0，tk]，有

因此，對所有t≥t0，‖φk(t)‖<ε，‖φk(tk)‖=‖yk‖<ε，與(12)式矛盾.

注意φ∈A(t2，xψ(t2))，因此，

(13)

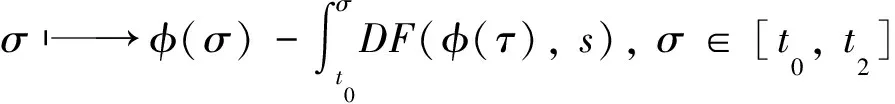
的兩種情況：

1)假設對v∈[t0，t2]，

在這種情況下，v∈[t0，t1]或v∈[t1，t2].如果v∈[t0，t1]，則

由于φ|[t0，t1]=yt，有

再由(13)式有

(14)

現在，假定v∈[t1，t2]，考慮到φ|[t1，t2]=y，有

(15)

因為x是廣義常微分方程(5)的解，我們推斷出

(16)

由(13)和(16)式，

(17)

再由(13)和(17)式，我們得到

(18)

2)假設對v∈[t0，t2]，

在這種情況下，v∈[t0，t1]或v∈[t1，t2].如果v∈[t0，t1)，因為φ|[t0，t1]=yt，則

(19)

現在，假設v∈[t1，t2]，考慮到φ|[t1，t2]=xψ，有

再由(13)式，有

(20)

在(14)，(18)和(20)式中，yt∈A(t1，xψ(t1))，有

V(t2，xψ(t2))≤V(t1，xψ(t1))

因此，

W(t2，yt2(t，ψ))≤W(t1，yt1(t，ψ))

由引理4可得(iv)顯然成立.

下面證明(v)：由引理4和引理8，考慮a是一個單位函數，對所有z∈X，t∈[t0，t0+σ]，

V(t，z)≤‖V(t，z)-V(t，0)‖≤‖z‖

下面證明(vi)：仿照證明(iii)的方法，對所有t∈[s0，t0+σ)和η>0，有

V(t+η，xψ(t+η))≤V(t，xψ(t))

即

V(t+η，xψ(t+η))-V(t，xψ(t))≤0

因此

定理2如果測度泛函微分方程(4)的平凡解y≡0是正則吸引的，則存在一個泛函

滿足：

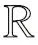
(iv)對所有t∈[t0，t0+σ]，W(t，0)=0；

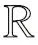
(21)

注意φη∈A(t+η，y(t+η)).因此

的兩種情況：

1)假設對V∈[t0，t+η]，

考慮到φη|[t0，t]=φ和φη|[t，t+η]=xψ，有

又因為φ∈A(t，xψ(t))，有

V(t+η，xψ(t+η))≤V(t，xψ(t))e-η

所以，

V(t+η，xψ(t+η))-V(t，xψ(t))≤V(t，xψ(t))(e-η-1)

因此，

因此，

2)假設對V∈[t0，t+η]，

因為情況2)的證明過程與定理1中(iii)的情況2)的證明過程相似，因此在這里省略.