高超聲速飛行器線性變參數一體化式控制律設計

楊 庶， 錢云霄， 楊 婷,2

(1. 西北工業大學 自動化學院，西安 710072； 2. 北京空天技術研究所，北京 100074)

高超聲速飛行器可進行跨空域、跨速域飛行，其復雜的飛行環境和時變的飛行動態給控制系統的設計帶來嚴峻挑戰.針對上述問題，目前常采用動態逆控制、反演控制、滑模控制、切換控制、自適應控制、線性變參數(LPV)控制等方法進行控制器設計.文獻[1]針對制導控制一體化問題，提出一種基于魯棒動態逆的動態面一體化算法，通過引入動態面控制，避免反演控制的“計算膨脹”問題.文獻[2]設計了一種無需在線求導的高超聲速飛行器反步法控制律方法，用于實現高超聲速飛行器縱向通道的航跡傾斜角跟蹤控制.模型的強非線性和強耦合性特點使得動態逆、反步法等控制器設計過程復雜，增加了實際應用難度[1,3].對于高超聲速飛行器縱向控制通道的速度和高度控制問題，文獻[4]設計干擾補償器和狀態反饋控制律，在實現指令跟蹤的同時，提高飛行器閉環系統相對于外界擾動的魯棒性.文獻[5]給出一種基于模糊控制理論的高超聲速飛行器縱向最優控制律，能夠在飛行器未建模動力學特性的影響下，實現對飛行器高度和速度指令的跟蹤.文獻[6]采用有限時間滑模控制理論，設計高超聲速飛行器在俯沖段的協同制導律，實現多枚高超聲速飛行器攻擊同一固定目標的控制任務.文獻[7-8]分別采用滑模和自適應控制理論實現高超聲速飛行器俯沖段的控制.文獻[9]針對吸氣式高超聲速飛行器的縱向飛行控制，建立多胞剛性LPV模型，進而基于區域極點配置實現系統的H∞/H2多目標魯棒控制.文獻[10]將切換控制思想與LPV控制結合，通過減小子系統的參數變化范圍，增強系統的魯棒性.

上述控制方法中，LPV控制利用參數依賴的思想，既可以有效適應高超聲速飛行器飛行包線大、參數快時變的特點，又可以基于增益調度技術保證閉環系統的穩定性和控制器的實用性，在高超聲速飛行器控制中得到廣泛應用.需要指出的是，現有的飛行器LPV控制研究一般僅考慮飛行器縱向或橫航向動力學特性[11-12]，忽略縱向和橫航向通道之間的耦合.基于飛行器完整模型的LPV控制研究通常引入模型假設(如速度傾側角為0)，降低控制律的設計難度.

本文基于高度-水平航跡控制概念，將高超聲速飛行器三維航跡分解為豎直面航跡和水平面航跡，通過高度、速度、側滑角、偏航角控制，實現飛行器的三維航跡控制.基于高度-水平航跡控制概念，采用具有L2誘導范數控制性能的LPV控制方法，設計高超聲速飛行器的一體化式LPV控制律.在地心地固(ECEF)參考系下建立高超聲速飛行器的數學模型，通過數值仿真檢驗一體化式LPV控制律在測量噪聲影響下的控制性能.仿真結果表明，該控制律能夠跟蹤給定控制指令，并具有較好的噪聲抑制性能.

1 高超聲速飛行器數學模型

基于WGS84地球模型參數，在ECEF參考系(見圖1)下建立飛行器的非線性數學模型，在模型中考慮地球自轉、地球扁率、地球引力二階簡諧效應的影響.圖中：l和μ為大地經度和大地緯度；ωE為地球自轉速度；lE為地球自轉角；ECI代表地心慣性參考系；B代表機體參考系.為便于控制律設計，基于平板地球假設，建立飛行器的簡化非線性數學模型，進而得到高超聲速飛行器的LPV模型.在兩組數學模型中均假設飛行器為剛體，并忽略飛行器的質量變化.

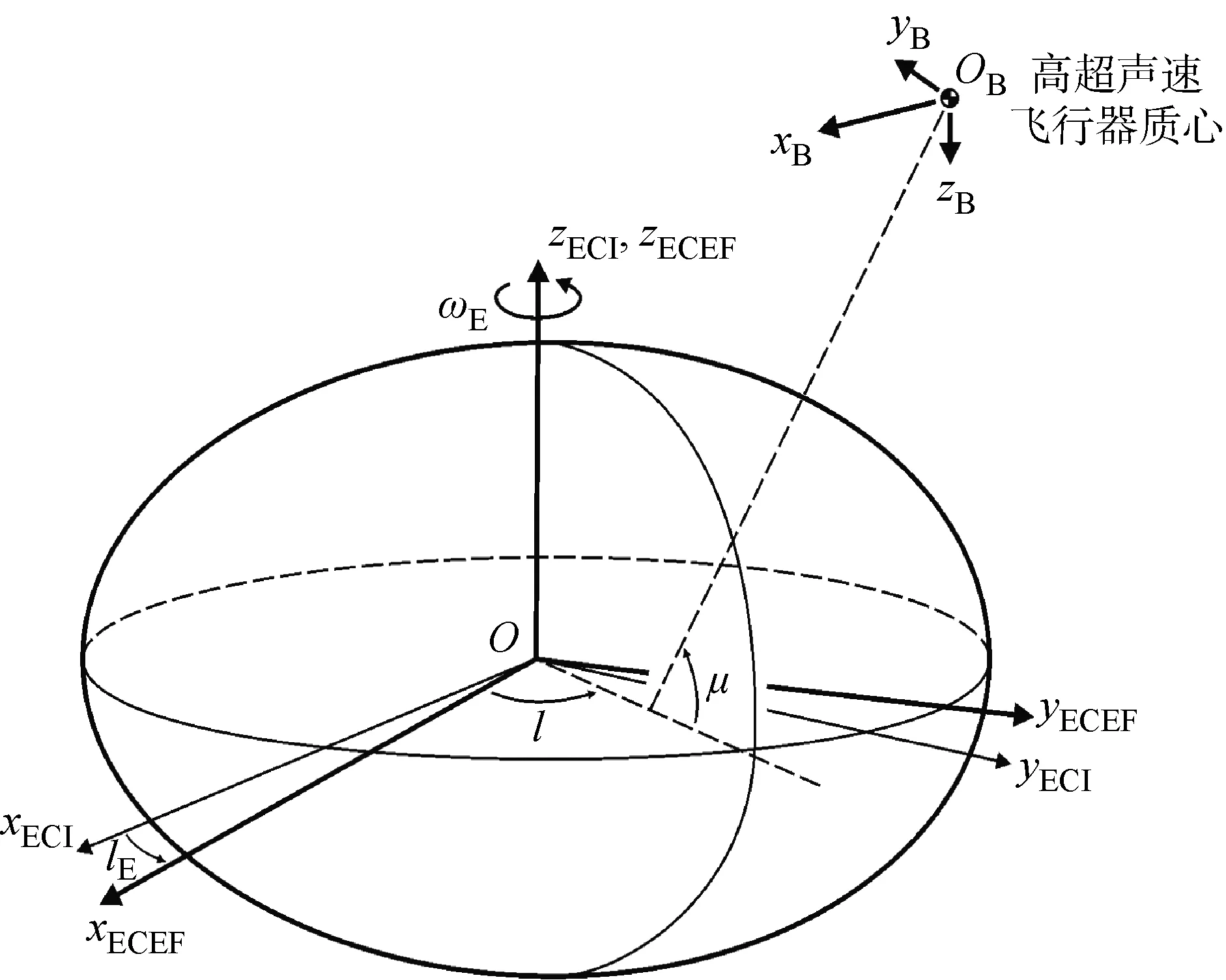
圖1 ECEF參考系與機體參考系示意圖Fig.1 ECEF reference frame and body reference frame

1.1 ECEF參考系下的運動方程

由于地球自轉的影響，圖1所示的ECEF參考系是相對于ECI參考系的非慣性參考系，其角速率向量為

(1)

(2)

在ECEF參考系中，高超聲速飛行器的平動運動受到地球自轉角速度、Coriolis效應、地球扁率等因素影響，根據牛頓第二定律，在機體參考下可將高超聲速飛行器的平動動力學方程表達為

(3)

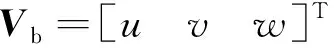
ge=

(4)

式中：GM為地心引力常數；J2為地球引力二階簡諧效應常數；a為地球半長軸；μc為地心緯度；rk(k=1,2,3)為飛行器位移向量r的第k個分量；‖r‖為飛行器相對于地心的距離.GM，J2，a均根據WGS84地球模型參數確定，式(3)和(4)的詳細推導過程參見文獻[13].

根據文獻[14]中的氣動參數進行計算，有

Fb=

(5)

式中：α為迎角；T為發動機推力，可通過燃油流量比δt進行控制；D，L和Y為飛行器的阻力、升力和側力，可分別通過副翼舵偏角δa、升降舵舵偏角δe和方向舵舵偏角δr進行控制.

高超聲速飛行器的轉動動力學方程為

(6)

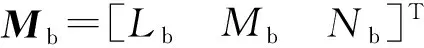
ωb=ωbn+Rbnωne+Rbeωe

(7)

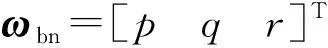
(8)

高超聲速飛行器的位移和四元數姿態運動學方程為

(9)

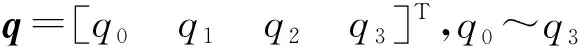
1.2 平板地球假設下的運動方程和LPV模型

為便于控制律設計，可忽略地球自轉和引力二階簡諧效應，根據式(3)、式(6)和式(9)進行簡化，在平板地球假設下建立高超聲速飛行器的簡化運動方程[13]，即

(10)

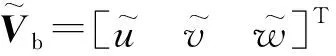
根據基于線性化的LPV模型建模方法[16]，可將式(10)轉化為如下高超聲速飛行器LPV模型，即

(11)

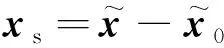
2 一體化式LPV控制律

針對高超聲速飛行器的三維航跡控制需求，基于高度-水平航跡控制概念設計高超聲速飛行器一體化式LPV控制律，進而采用線性矩陣不等式(LMI)方法求解該LPV輸出反饋控制律的參數.

2.1 高度-水平航跡控制概念

根據笛卡爾參考系中基向量相互正交的性質，可根據北東地參考系，將高超聲速飛行器的三維航跡控制問題分解為水平面和豎直面航跡控制問題(見圖2).豎直面航跡控制可通過高度控制實現，水平面航跡控制問題可通過速度和偏航角控制實現.由于高超聲速飛行器通常要求實現協調轉彎性能，即水平面航跡控制時側滑角為0°，所以側滑角控制應作為水平面航跡控制目標之一.

根據上述討論，控制指令可選：速度V、側滑角β、高度h、偏航角ψ.由于這些控制指令既包含常規飛行控制的內回路姿態控制指令，也包含外回路控制指令，所以通常需要進行內外回路控制律的分離設計與綜合，進而實現飛行器三維航跡控制.由于內外回路控制律分離設計方法有可能導致控制律之間的耦合問題，所以本文采用LPV輸出反饋控制理論，設計高超聲速飛行器一體化式LPV飛行控制律，使用LMI方法求解具有L2誘導范數性能的LPV魯棒控制律參數.

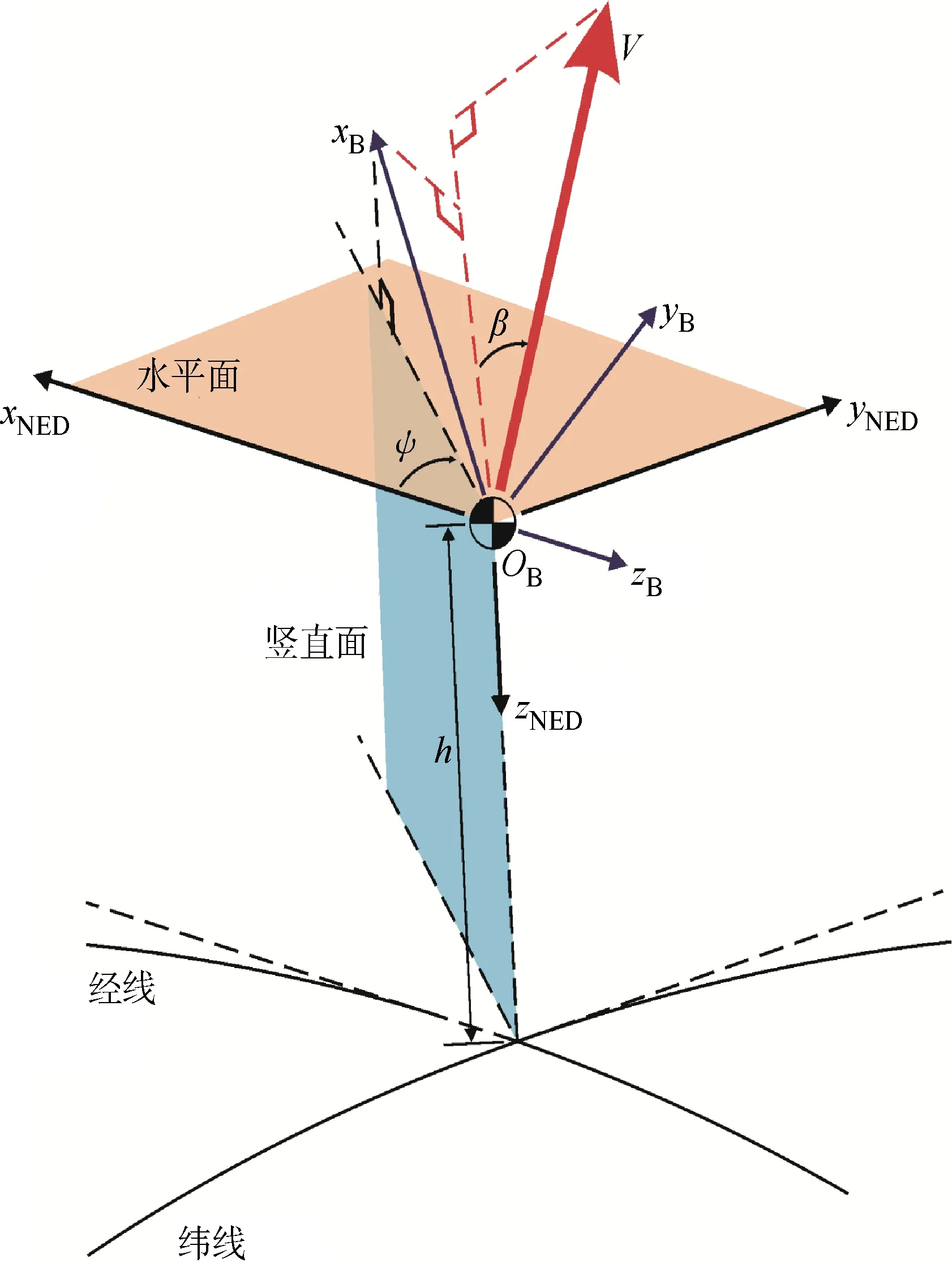
圖2 高度-水平航跡控制概念示意圖Fig.2 Altitude-horizontal trajectory control concept

2.2 LPV控制律設計

高超聲速飛行器一體化式LPV控制律如圖3所示，通過參考模型和L2誘導范數意義下的模型匹配方法[17]，實現速度、側滑角、高度、偏航角通道的模型跟蹤控制性能.圖中：下標c代表控制指令；向量n為反饋噪聲.各控制通道的參考模型均為阻尼比0.7的二階系統，則有傳遞函數：

(12)

式中：s為傳遞函數的復頻域自變量.

誤差權值函數設計為

(13)

式中：WV(s)和Wh(s)的低頻增益為0.01，設計目標為使速度和高度的穩態控制誤差不超過1%；Wβ(s)和Wψ(s)的低頻增益為0.001，設計目標為使側滑角和偏航角的穩態控制誤差不超過0.1%.

控制權值函數設計為

(14)

其設計目標為在單位指令信號的作用下，高超聲速飛行器燃油流量的變化量不超過20%，副翼、升降舵、方向舵的變化量不超過10°.式(13)和式(14)中各權值函數的輸出分別對應于圖3中的eV、eβ、eh、eψ和eu.

反饋信號設計為

xf=

(15)

各反饋信號均受測量噪聲影響.

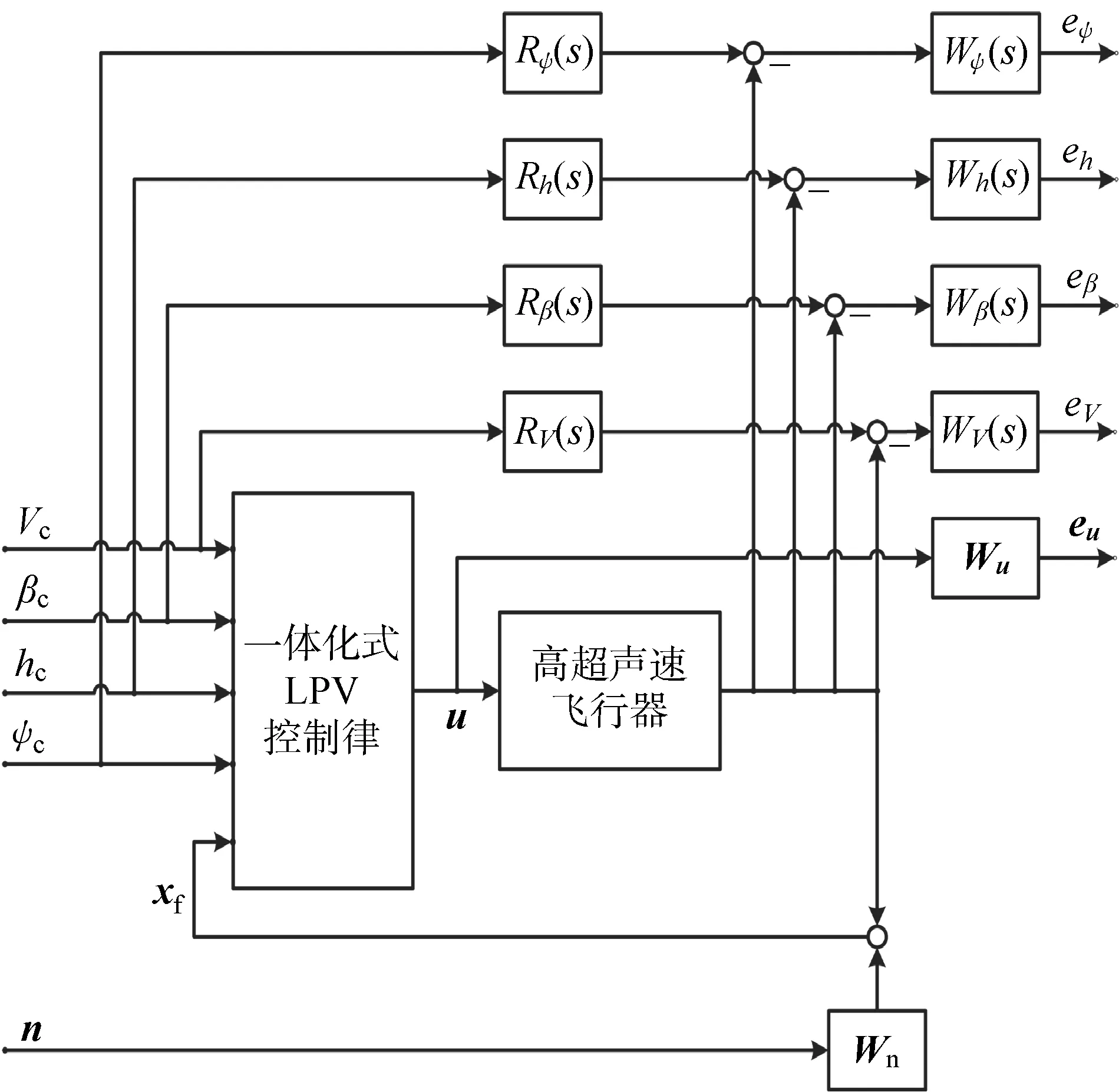
圖3 LPV控制律與系統連接結構Fig.3 System interconnections for LPV control law

噪聲權值函數設計為

Wn=

(16)

式中：I3和I6分別為三維單位矩陣和六維單位矩陣.式(16)代表速度、位移、角度和角速率反饋信號的噪聲幅值分別不超過0.01 m/s、0.01 m、0.01° 和 1.75×10-4rad/s.

根據式(11)～(16)，用于控制律設計的LPV模型可表達為

(17)

式中：xL為狀態變量，包括式(11)～(13)的狀態變量；d為廣義輸入，包括控制指令和測量噪聲；e為廣義誤差，由式(13)的輸出信號給定；y為輸出信號，由控制指令和反饋信號給定.對于式(17)中的線性系統，A為系統狀態矩陣，B1為廣義輸入的輸入矩陣，B2為控制輸入的輸入矩陣，C1為廣義誤差的輸出矩陣，C2為輸出信號的輸出矩陣，D11為從廣義輸入到廣義誤差的前饋矩陣，D12為從控制輸入到廣義誤差的前饋矩陣，D21為從廣義輸入到輸出信號的前饋矩陣.

控制律在馬赫數包線內進行設計，所采用的馬赫數包線為4≤Ma≤6.為保證LMI的約束條件為有限維，采用如下的包線離散網格進行控制律參數求解：

P=

{4, 4.25, 4.5, 4.75, 5, 5.25, 5.5, 5.75, 6}

(18)

LPV控制器參數通過求解如下的LMI進行確定[18]，即

(19)

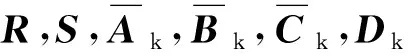
(20)

式(19)中的LMI使閉環系統具有D-穩定性[18-19]，并且保證閉環系統滿足如下的L2誘導范數性能，即輸入-輸出L2穩定性:

(21)

LPV控制律可表達為

(22)

控制律的參數可通過下式計算：

(23)

式中：矩陣N為中間變量.式(23)的具體推導過程參見文獻[18].式(19)中的待求矩陣采用如下的參數化格式，即

(24)

式中：0, 1, 2代表階次；ρ定義為ρ=(Ma-4)/2.矩陣R(ρ)表達為馬赫數的二次方程形式，使控制律能夠對高超聲速飛行器在不同飛行速度下的運動特性非線性變化進行有效控制.其余待求矩陣均設為常數矩陣，降低控制律求解和實現所需計算量.

3 仿真結果

基于高超聲速飛行器平板地球假設下的運動方程，分析飛行器開環系統和閉環系統的穩定性.采用ECEF參考系下的高超聲速飛行器運動方程，通過豎直面機動和水平面機動的數值仿真，檢驗一體化式LPV控制律的控制性能和魯棒性.

3.1 穩定性分析

根據平板地球假設下的運動方程，高超聲速飛行器在馬赫數包線4≤Ma≤6中的極點分布如圖4所示.圖中：zb為飛行器的極點；ωn和ξ分別為飛行器極點的自然頻率和阻尼比.由圖可見，飛行器是開環不穩定系統，不穩定極點的最高自然頻率接近于10 rad/s，說明該飛行器的開環不穩定性較高，而本文設計的一體化式LPV控制律能夠保證閉環系統為穩定系統，并且所有極點在復平面上均分布在阻尼比大于0.5、自然頻率小于30 rad/s的扇形區域內，實現式(19)給定的閉環系統D-穩定性要求.同時，閉環系統的大多數極點的阻尼比大于0.7，說明一體化式LPV控制律能夠為高超聲速飛行器閉環系統提供良好的阻尼特性.

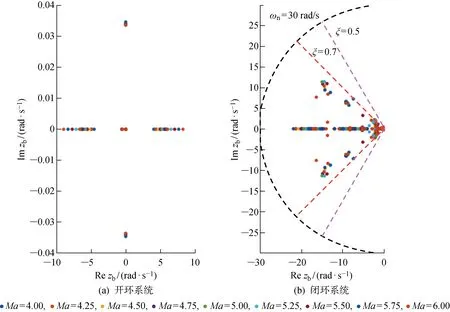
圖4 高超聲速飛行器開環和閉環系統極點分布Fig.4 Open-loop and closed-loop poles of a hypersonic vehicle

3.2 躍升加速機動

采用ECEF參考系下的高超聲速飛行器運動方程進行數值仿真，使飛行器在豎直面內進行高度躍升和水平加速機動，檢驗基于飛行器簡化模型設計的LPV控制律在地球自轉、地球扁率、地球引力二階簡諧效應等擾動下的控制性能.仿真中，在反饋信號中增加測量噪聲，檢驗該控制律相對于噪聲的魯棒性.速度、位移、角度和角速率反饋信號的噪聲幅值分別設置為0.005 m/s、0.005 m、0.005°和8.726×10-5rad/s.

如圖5所示，一體化式LPV控制律能夠使高超聲速飛行器跟蹤給定的高度和速度指令，機動過程中側滑角和偏航角沒有出現明顯的控制誤差.同時，測量噪聲對飛行器閉環系統控制性能的影響很小，沒有出現控制性能惡化的現象.圖中：t為時間.從圖6和圖7所示的高超聲速飛行器在ECEF參考系下的狀態變量響應可以看出，高超聲速飛行器具有閉環穩定性，說明該控制律在地球自轉、地球扁率、地球引力二階簡諧效應等擾動和測量噪聲的影響下仍具有良好的控制性能和魯棒性.

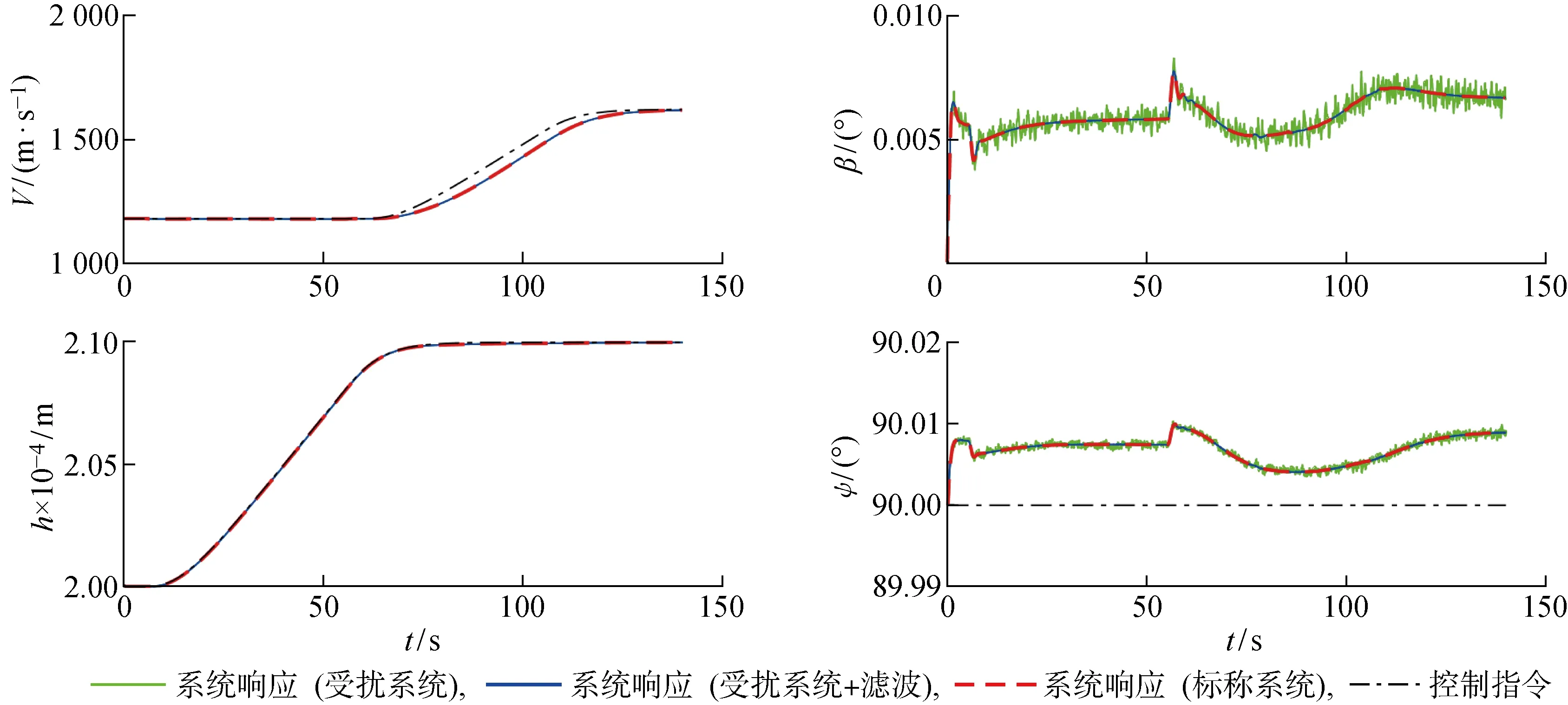
圖5 控制指令與系統響應(躍升加速機動)Fig.5 Control commands and system responses (ascent-acceleration maneuver)

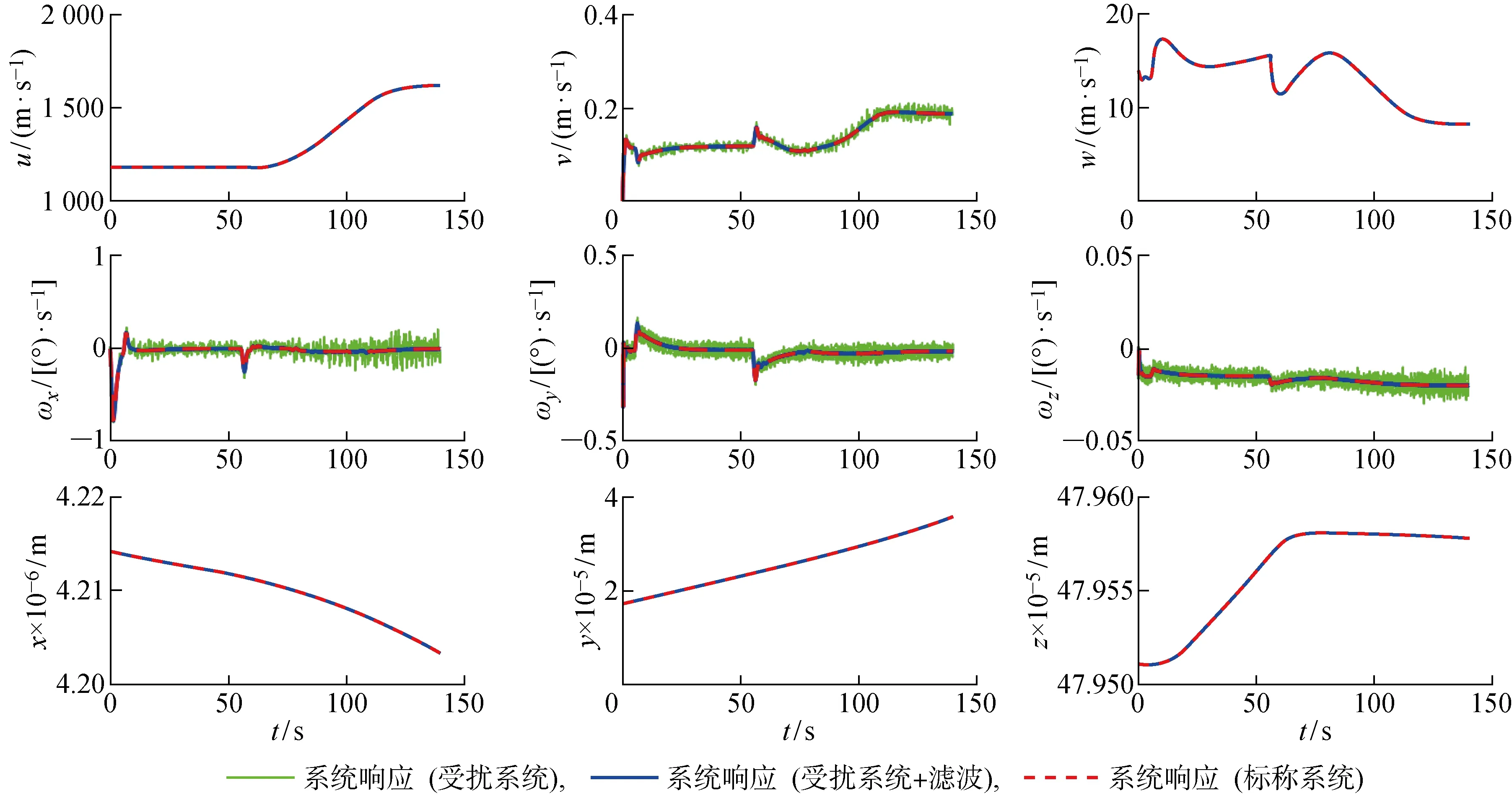
圖6 ECEF參考系下高超聲速飛行器運動方程的狀態響應(躍升加速機動)Fig.6 State responses of hypersonic vehicle equations of motion in ECEF reference frame (ascent-acceleration maneuver)

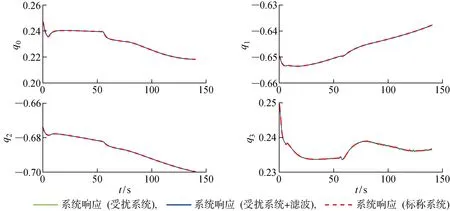
圖7 ECEF參考系下高超聲速飛行器的姿態四元數響應(躍升加速機動)Fig.7 Quaternion responses of hypersonic vehicle equations of motion in ECEF reference frame (ascent-acceleration maneuver)

從圖8所示的控制輸入可以看出，在標稱條件下高超聲速飛行器完成躍升加速機動所需的控制輸入量較小.但在測量噪聲的影響下，LPV控制律輸出的控制輸入中包含較為明顯的噪聲，不利于實際應用.為消除該噪聲影響，在LPV控制律的反饋信號中增加二階低通濾波器：

(25)

式中：濾波器自然頻率ωf=40 rad/s；阻尼比ξf=1.

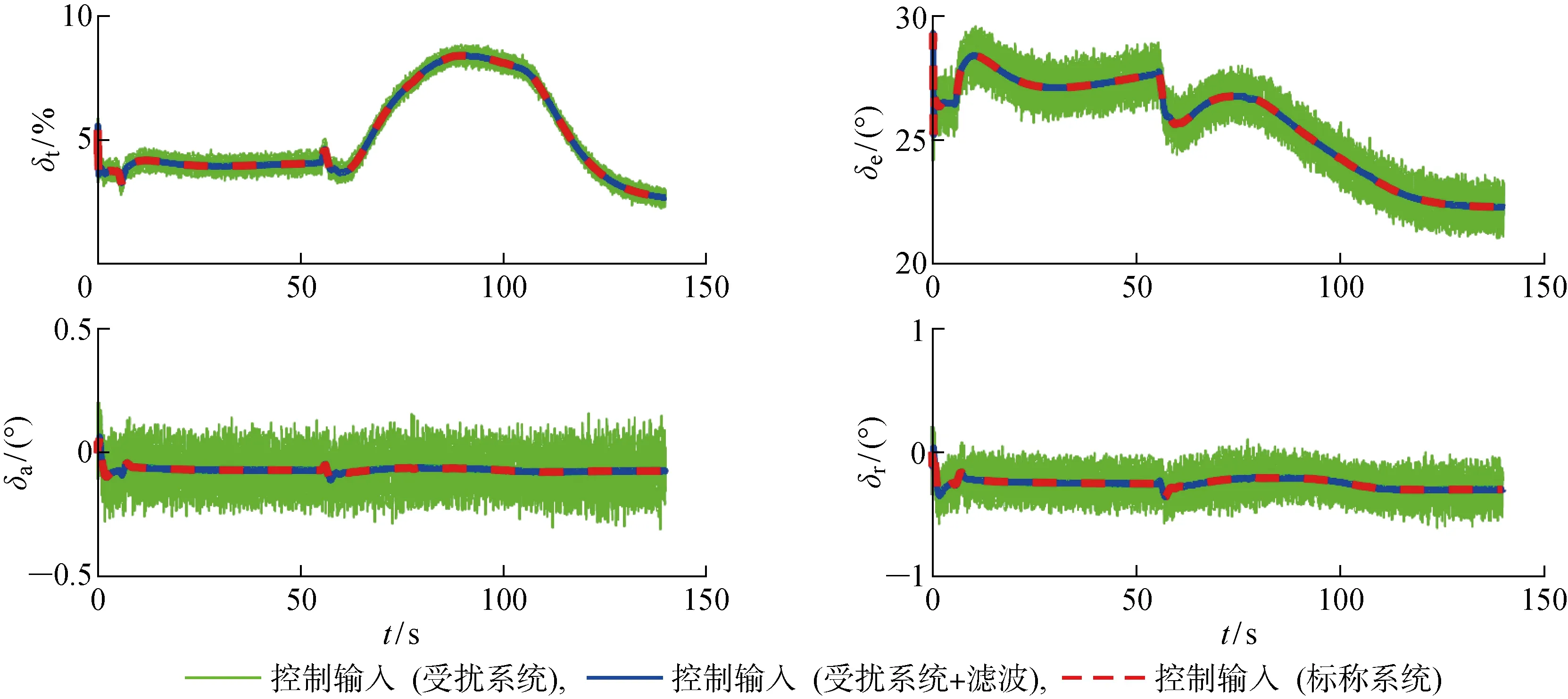
圖8 控制輸入(躍升加速機動)Fig.8 Control inputs (ascent-acceleration maneuver)

從圖5～7的仿真曲線中可以看出，對反饋信號進行濾波后，高超聲速飛行器閉環系統在測量噪聲的影響下仍然具有良好的響應特性，并且LPV控制律生成的控制輸入得到明顯的降噪和平滑化.

3.3 水平轉彎機動

采用ECEF參考系下的高超聲速飛行器運動方程進行數值仿真，使飛行器在水平面內進行水平轉彎機動.仿真中，在反饋信號中增加測量噪聲，噪聲幅值設置與3.2節相同.

從圖9可以看出，一體化式LPV控制律能夠使高超聲速飛行器跟蹤給定的偏航角指令，使飛行器完成45°的水平轉彎機動，機動過程中側滑角的控制誤差小于0.2°，說明飛行器實現了協調轉彎控制性能.同時，測量噪聲對飛行器閉環系統的控制性能影響很小，沒有出現控制性能惡化的現象.

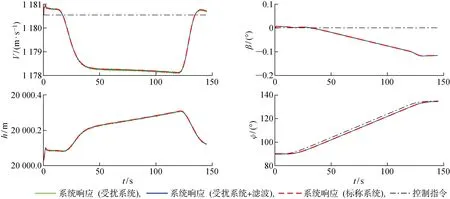
圖9 控制指令與系統響應(水平轉彎機動)Fig.9 Control commands and system responses (level turn maneuver)

從圖10和圖11所示的高超聲速飛行器在ECEF參考系下狀態變量響應可以看出，高超聲速飛行器具有閉環穩定性，說明該控制律在地球自轉、地球扁率、地球引力二階簡諧效應等擾動和測量噪聲的影響下仍具有良好的控制性能和魯棒性.從圖12所示的控制輸入可以看出， 高超聲速飛行器完成水平轉彎機動所需的控制輸入量較小.

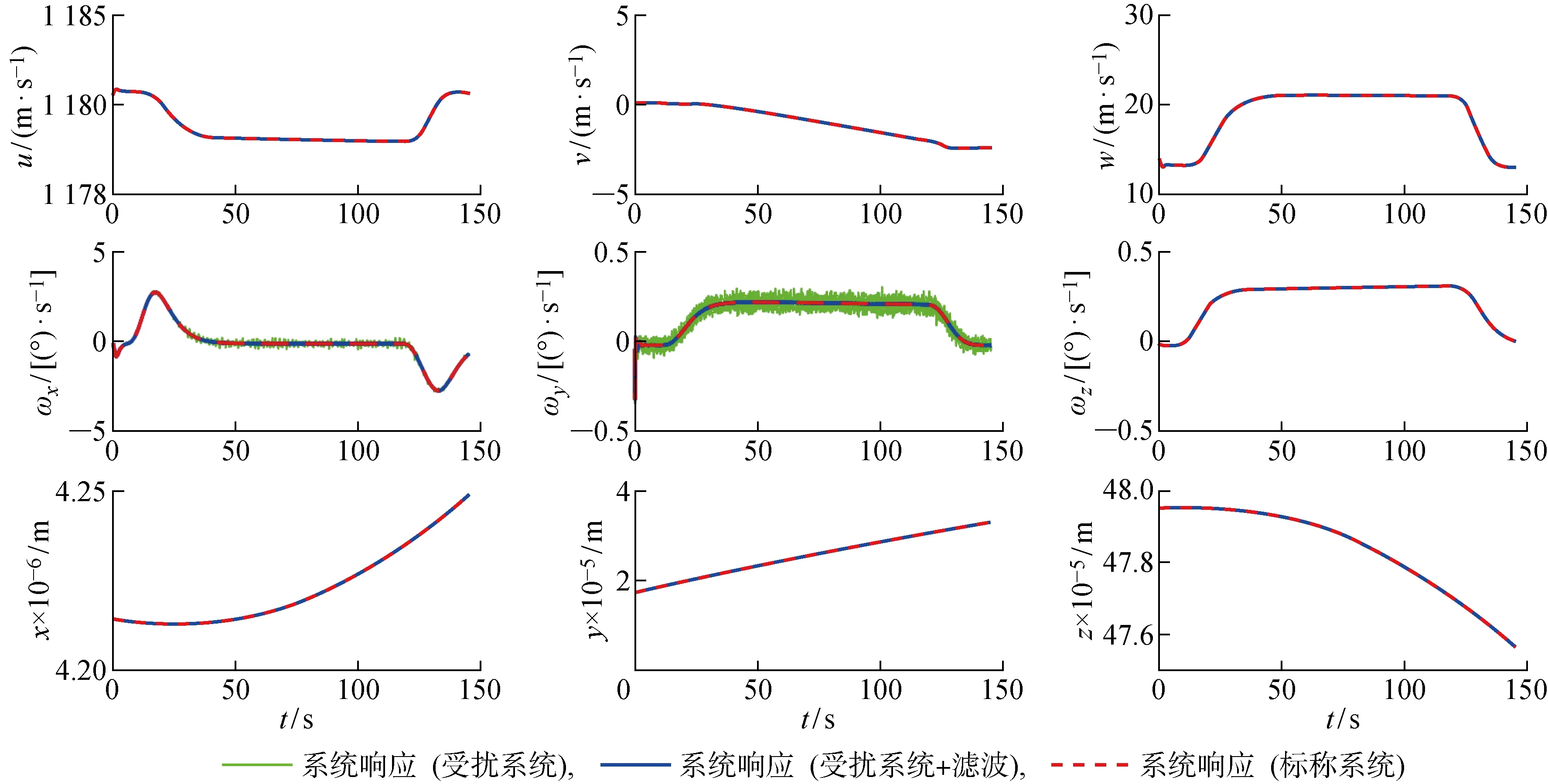
圖10 ECEF參考系下高超聲速飛行器運動方程的狀態響應(水平轉彎機動)Fig.10 State responses of hypersonic vehicle equations of motion in ECEF reference frame (level turn maneuver)

圖11 ECEF參考系下高超聲速飛行器的姿態四元數響應(水平轉彎機動)Fig.11 Quaternion responses of hypersonic vehicle equations of motion in ECEF reference frame (level turn maneuver)

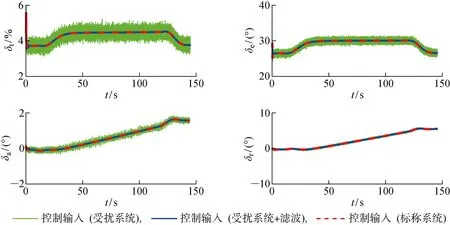
圖12 控制輸入(水平轉彎機動)Fig.12 Control inputs (level turn maneuver)

從圖9～12中的仿真曲線可知，在應用式(25)中的二階低通濾波器對反饋信號進行濾波后，測量噪聲對控制輸入的影響得到明顯的抑制，同時LPV控制律仍能夠保持良好的控制性能.

4 結論

針對高超聲速飛行器三維航跡控制問題，基于高度-水平航跡控制概念，設計了一體化式LPV控制律.該控制律不區分常規飛行控制的內外控制回路，在L2誘導范數意義下具有良好的控制精度和魯棒性，具體結論如下：

(1) 高度-水平航跡控制概念基于笛卡爾參考系基向量相互正交的性質，將三維航跡控制問題轉化為水平面和豎直面航跡控制問題，等價的控制指令為速度、側滑角、高度和偏航角.

(2) 一體化式LPV控制律在馬赫數包線內進行設計，在4≤Ma≤6包線內使高超聲速飛行器閉環系統具有L2誘導范數控制性能，在保證控制指令跟蹤精度的同時，實現相對于噪聲的魯棒性.

(3) 基于極點配置和LMI方法設計的一體化式LPV控制律使高超聲速飛行器閉環系統的極點具有阻尼比不低于0.5、自然頻率不高于30 rad/s的性能.

(4) 采用ECEF參考系下建立的高超聲速飛行器運動方程進行數值仿真，一體化式LPV控制律能夠在地球自轉、地球扁率、地球引力二階簡諧效應等擾動下保持良好的控制性能，并且相對于反饋信號中的測量噪聲具有良好的魯棒性.