初中數學有效復習“精講精練”教學法
——以“二次函數與反比例函數”為例

?安徽省蒙城縣莊子中學 杜 宇

1 引言

復習課是為了讓學生回顧、鞏固、消化、歸納數學基礎知識，提高分析、解決問題的能力.一堂有效的數學復習課，不僅能夠讓學生鞏固知識、查漏補缺，而且要溫故知新.

初中數學復習“量大、面廣、知識點多、時間緊”，要讓學生在短時間內系統有效地復習，“精講精練”不失為一種行之有效的方法.教師要認真篩選和精心設計一定量的具有“概念性、典型性、針對性、綜合性、啟發性、思考性、靈活性、創造性”等特點的例題、習題，通過“精講精練”來達到鞏固與提高的目的[1].

“二次函數與反比例函數”，是滬科版九年級上冊第21章的內容.本章共有6節，復習的量大、面寬、時間緊，不可能做到面面俱到，只能“突出重點、化解難點、以點帶面”.因此，本章復習的重難點是：熟練掌握和運用二次函數、反比例函數的圖象和性質，培養在解決實際問題時建立函數模型的意識，并能掌握建立函數模型的技能.精選適量的典型例題，精講、分析解決這些問題，做到以點帶面，是本章復習教學的主要方法[2].下面通過典型例題來了解和掌握“精講精練”復習法.

2 “精講精練”復習教學法的運用

2.1 “小題大做”收奇效

例1已知x=5時，y=x2+px+q的最小值為-2，則p=______,q=______.

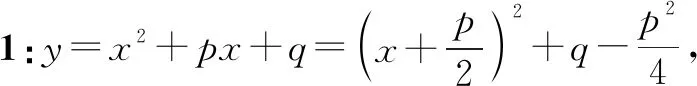
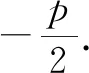
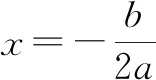
2.2 歸類訓練找方法

歸類訓練就是把類型相同或相似的題型放在一起，只要講(練)一個或幾個題目，就可以找到并掌握解決這類問題的方法與技巧，避免陷入題海而不能自拔，達到觸類旁通、以點帶面、舉一反三的效果.

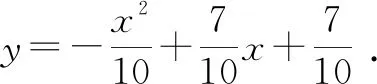
(1)試寫出年利潤S(單位：萬元)與廣告費x的函數關系式，并計算廣告費是多少萬元時，公司獲得的年利潤最大，最大年利潤是多少萬元？

(2)把(1)中的最大利潤留出3萬元做廣告，其余的資金投資新項目.現有6個項目可供選擇，各項目每股投資金額和預計年收益如表1.

林業局窗口打造快速高效服務通道。對申請人提出的申請事項，只要申報材料齊全，可以當場辦結的，立即辦結；當場不能辦結的，說明原因，并把需補齊的材料一次性告知對方。同時，注重加強對行政許可事項的審核和審批工作的督辦，最大程度的提高審批效率，真正把林業窗口建設成為服務經濟、方便群眾的“民心窗口”，轉變政府職能、提供工作效能的“示范窗口”，周到熱情、便民利民的“形象窗口”。

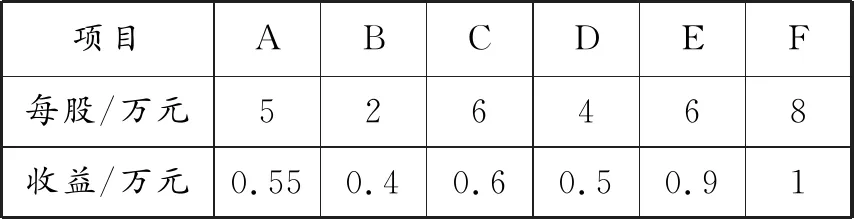
表1 各項目每股投資金額與預期收益

如果每個項目只能投一股，且要求所有投資項目的收益總額不得低于1.6萬元，那么有幾種符合要求的投資方式？寫出每種投資方式所選的項目.

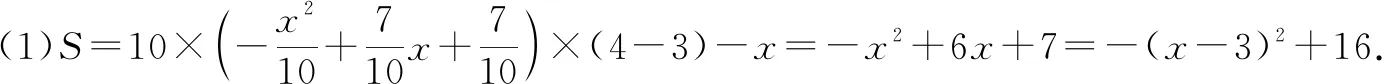
當x=3時，年利潤S取得最大值16.

所以，當廣告費是3萬元時，公司獲得的最大年利潤是16萬元.

(2)用于再投資的資金是16-3=13(萬元)，經分析，有兩種投資方式符合要求：

一種是取A，B，E各一股，投入資金為5+2+6=13(萬元)，收益為0.55+0.4+0.9=1.85(萬元)>1.6(萬元)；另一種是取B，D，E各一股，投入資金為2+4+6=12(萬元)<13(萬元)，收益為0.4+0.5+0.9=1.8(萬元)>1.6(萬元).

點評:本題屬于“獲取最大利潤”類習題，實際上就是求二次函數的最大值或最小值.解這類題型首先要明確利潤=(銷售單價-每件成本)×銷售量；然后求出函數表達式和自變量的取值范圍，再通過配方變形，或利用公式求出最大值或最小值.要注意的是，由此求得的最大值或最小值對應的自變量的值必須在自變量的取值范圍內，若忽視了自變量的取值范圍往往會造成解題錯誤.

2.3 一題多解拓思路

通過對典型例題解法的講練與拓展，有針對性地引導學生進行一題多解訓練，以拓寬學生的解題思路，不斷提高學生靈活運用各種知識的綜合能力.

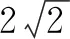
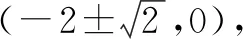
所以,拋物線的解析式為y=x2+4x+2.

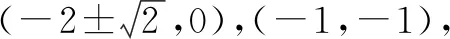
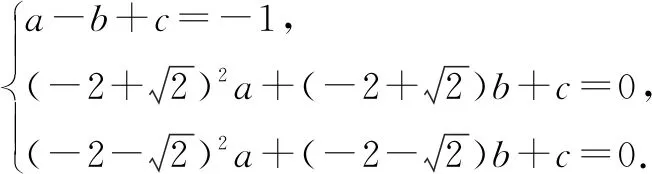
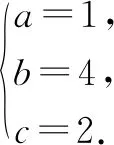
所以,所求解析式為y=x2+4x+2.

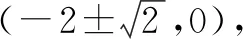
3 結論

教學實踐表明，初中數學復習課中，采用“精講精練”法，以例題為中心，通過小題大做、歸類訓練、一題多解等方式來組織教學，將某一章節內容的基本知識串起來講練，既能鞏固加深已學過的舊知識，又能夠讓學生熟練掌握多種題型的解題方法與技巧[3].