正方形對角線性質的再探究

?寧波科學中學 王 震

1 引言

正方形是初中數學的一個重要內容，因其具有獨特的圖形特點、圖形風格、圖形性質，也是中考的一個重要考點，特別是正方形的對角線更值得深入探究.下面就一起走進正方形對角線的探究天地，共賞正方形的美景！

2 性質探究

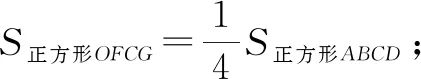
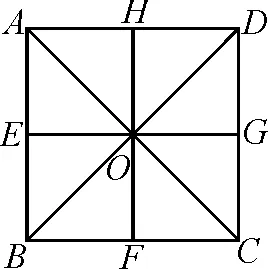
圖1

下面給出性質①的幾種證明，供學習時借鑒.

證法1：三角形全等法.

因為四邊形ABCD是正方形，對角線AC，BD相交于點O，所以∠OCF=∠OCG=45°.

因為OG⊥CD，OF⊥BC，所以∠OFC=∠OGC=90°.又OC=OC，所以△OFC≌△OGC.即得OG=OF.

證法2：三角形面積法.

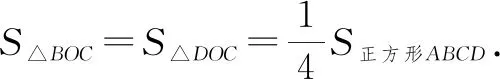
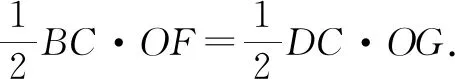
這里僅提供兩種常見的證明方法，供參考.其余性質的證明讀者感興趣的，可以嘗試自己完成.

3 性質應用

3.1 借助四邊形的面積，求正方形的邊長

例1(2021·重慶中考)如圖2，正方形ABCD的對角線AC，BD交于點O，M是邊AD上一點，連接OM，過點O作ON⊥OM，交CD于點N．若四邊形MOND的面積是1，則AB的長為( ).

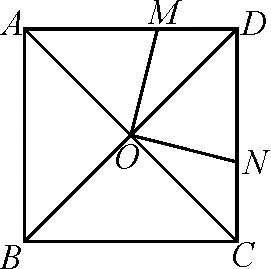
圖2

解析：如圖3，過點O分別作OG⊥AD，垂足為G，OH⊥CD，垂足為H.根據性質，得OG=OH.

圖3

∵OH⊥OG，OM⊥ON，

∴∠GOM=∠HON，

∠OGM=∠OHN.

∴△OGM≌△OHN.

故四邊形GOHD的面積等于四邊形MOND的面積，等于1.

由四邊形ABCD是正方形，則其面積為四邊形GOHD的面積的4倍，等于4，所以AB=2.

故選答案：C.

點評：根據正方形的特點，過正方形的中心引兩邊的垂線，利用三角形的全等，化已知四邊形的面積為正方形一角四邊形的面積，從而根據正方形的面積是一角四邊形面積的4倍計算即可.這個結論有著重要的應用，若遇到填空題或選擇題是可以直接運用，從而提高解題的效率.

3.2 構造中位線，求中位線的長

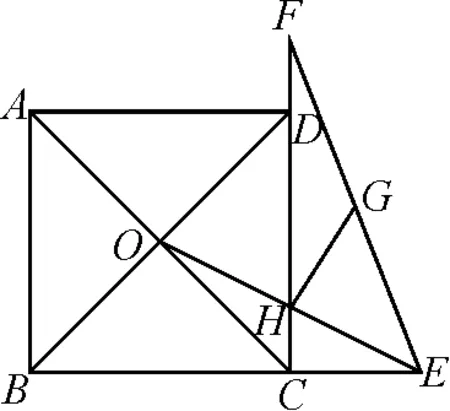
例2(2021年天津)如圖4，正方形ABCD的邊長為4，對角線AC，BD相交于點O，點E，F分別在BC，CD的延長線上，且CE=2，DF=1，G為EF的中點，連接OE，交CD于點H，連接GH，則GH的長為．

圖……