智慧引領 模型破冰
——對“圓周角(第1課時)”教學設計的思考

?湖北省咸寧市教育科學研究院 廖明芳

?湖北省咸寧實驗外國語學校 許麗琴 王 彎

1 問題呈現

九年級開始學習圓周角的概念，通過與已有“圓心角”概念對比得出圓周角概念，而在圓周角定理得出的環節，人教版數學教材九年級上冊第86頁用了下面這段文字：

如圖1,為了證明上面發現的結論(圓周角定理)，在⊙O任取一個圓周角∠BAC，沿AO所在直線將圓對折，由于A的位置不同，折痕會：(1)在圓周角的一條邊上；(2)在圓周角的內部；(3)在圓周角的外部.

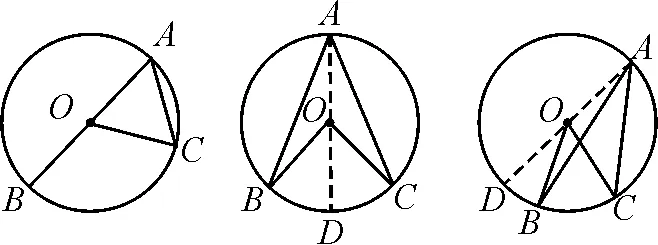
圖1

2 問題診斷

根據教材呈現內容，為引出圓周角的概念，很多教師設計了“將圓形紙片動手折一折”的教學環節，這樣圓周角的出現比較容易，進一步測量圓周角和同弧圓心角也不困難，于是順理成章“猜一猜”：一條弧所對的圓周角等于它所對的圓心角的一半.到了關鍵“證一證”環節，問題來了：(1)教材中的這條折痕在證明過程中意義非凡，如何出現？(2)圓心角和圓周角的位置關系為何直接導致證明過程的差異，以及如何分類？

基于以上兩個問題，教師用“折痕說”很難將問題自然過渡，只能采用強制引入的方式，憑空出現這條“折痕”，進而證明，使得整節課的邏輯鏈條斷裂，干擾、打亂學生思維.

3 問題解決

經過反復實驗，我們工作室的教師最終采用如下途徑來解決本節課的難點.

3.1 情境導入，引出新知

播放神舟十二號發射及其與天和核心艙對接過程的短視頻，抽象出圓周角，引出研究目標，同時增強學生的民族自豪感.

3.2 對……

登錄APP查看全文

猜你喜歡

模型學生

一半模型

童話王國·奇妙邏輯推理(2024年5期)2024-06-19 16:03:38

快把我哥帶走

作文大王·笑話大王(2021年4期)2021-04-26 19:00:35

重尾非線性自回歸模型自加權M-估計的漸近分布

數學物理學報(2020年2期)2020-06-02 11:29:24

《李學生》定檔8月28日

電影(2018年9期)2018-11-14 06:57:21

趕不走的學生

作文世界(小學版)(2018年4期)2018-10-16 17:13:34

學生寫話

快樂作文·低年級(2016年12期)2017-01-03 20:52:44

3D打印中的模型分割與打包

光學精密工程(2016年6期)2016-11-07 09:07:19

學生寫的話

快樂作文·低年級(2016年6期)2016-06-24 18:58:40

FLUKA幾何模型到CAD幾何模型轉換方法初步研究

核科學與工程(2015年4期)2015-09-26 11:59:03

一個相似模型的應用

中學數學雜志(初中版)(2006年1期)2006-12-29 00:00:00

中學數學 2022年20期

中學數學的其它文章

借助數學實驗 點亮數學課堂

基于思維能力培養的一節課堂教學評析
——從“正多邊形與圓”談起

“雙減”背景下初中數學錯題資源的有效利用

初中數學“問題引領課堂”的實踐與思考

正方形對角線性質的再探究

“雙減”政策下數學作業設計及思考