基于LF1352森林運載車的履帶板仿生設計及通過性

劉九慶， 李新源， 孫術發

（東北林業大學 a. 機電工程學院， b. 工程技術學院， 哈爾濱 150040）

1 仿北極熊熊爪結構的履帶設計

1.1 履帶板形狀設計

自然界很多動物都擁有在復雜道路上行走的能力，這得益于它們特殊的足部結構[11].北極熊是一種生活在北極的世界最大食肉動物之一.北極熊擁有在冰雪路面上快速奔跑的能力，這也源于它們特殊的足部結構.北極熊的熊掌寬超過25 cm，爪子長度可達10 cm.當北極熊在冰雪路面上行走時，尖銳的腳趾會插入堅硬的積雪中，積雪在擠壓區域內聚集，有利于增大北極熊腳掌的牽引力，北極熊腳印如圖1所示.

圖1 北極熊腳印圖Fig.1 Image of polar bear footprint

通過對北極熊的熊爪進行研究，對履帶板形態進行仿生設計，履帶板花紋的三角形區域和兩側的嚙合部分相當于北極熊熊爪的腳趾區域，使履帶板輕易地扎入積雪來增大附著力.履刺中間的四邊形空腔相當于北極熊的腳掌擠壓部分，這種履帶板在運動過程中可以限制積雪的流動，減少積雪流失，增大履帶車輛在積雪路面的通過性.履帶板通過銷軸進行鏈接，履刺花紋如圖2所示.

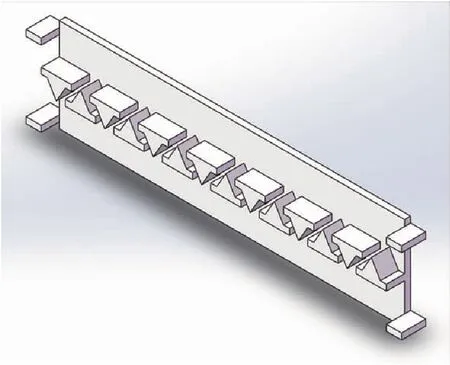
圖2 履刺花紋Fig.2 Track grouser pattern

履帶板節距計算公式為

（1）

式中，m為履帶車的質量.履帶板寬度為

B=（0.2～0.4）L

（2）

式中，L為履帶板整體長度.

1.2 履帶板驅動輪嚙合部位設計

將履帶板和驅動輪嚙合部分設計在履帶板的兩側，履帶車在行進過程中，驅動輪可以限制履帶板的水平自由度.嚙合部分的高度過大會對車體產生影響，因此嚙合部位的高度等同于履刺的深度，以增大履帶板受到的剪切力.履帶板嚙合部分尺寸如圖3所示（單位：mm）.

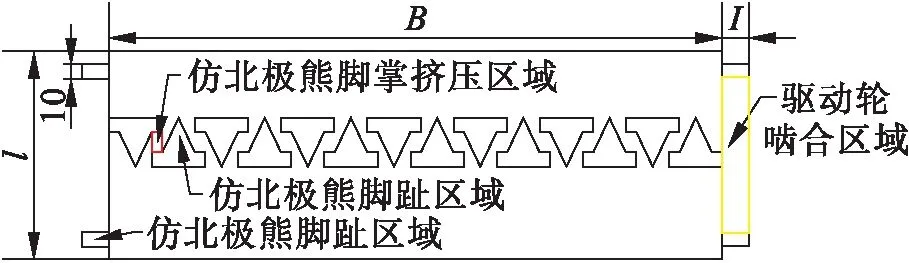
圖3 擠壓區域及整體尺寸簡化示意圖Fig.3 Simplified schematic diagram of extrusion area and overall size

2 力學計算

履帶車輛在行駛過程中，履帶板受到重力的作用發生下陷，履刺完全扎入積雪中，并發生水平方向位移.履帶車輛在行駛過程中的牽引能力主要由履帶板受到的牽引力決定，牽引力和土壤剪切力是一對相互作用力.通過研究履帶車輛在行駛過程中受到的土壤剪切力可以得出履帶車輛的通過性，積雪通常情況下被認為是一種特殊的土壤.履帶車輛受到的土壤剪切力一方面取決于車輛的設計參數，另一方面取決于土壤的力學性能.由于不同土壤的力學性能差異較大，所以需要設計適用于積雪路面的履帶板機構.由文獻[12]及[13]可知，履帶板在行駛過程中所受到的水平方向剪切力主要分為4個部分，分別為作用于履帶板上的力F1，作用于履刺底部的力F2，作用于履刺和嚙合部位上的力F3，作用于履帶板側面的力F4.履帶板的受力如圖4所示，履帶板履刺結構參數如圖5所示.

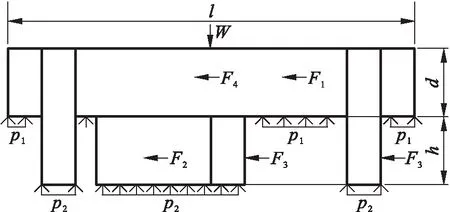
圖4 履帶板受力分析Fig.4 Force analysis of track shoes

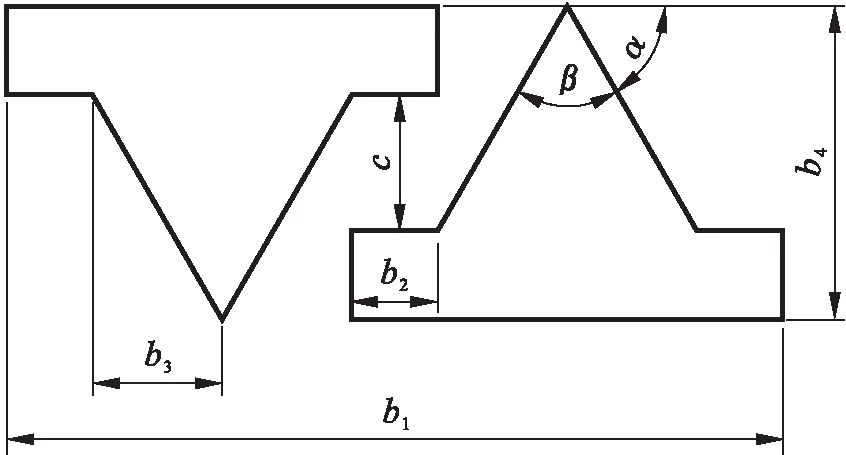
圖5 履刺結構參數Fig.5 Track grouser structure parameters

由Bekker沉積公式可知

（3）

式中：p為法向應力；kc為土壤粘聚變形模量；kφ為土壤內摩擦變形模量；z為土壤壓縮變形量；n為土壤變形指數.當履帶車輛在路面上行駛時，可以把Bekker沉積公式簡化為

p=Kzn

（4）

K可由式（5）推出，即

W=KznS1+K（z+h）nS2

（5）

式中：S1為履帶板底部的面積；S2為履刺底部的面積.作用于履帶板底部和履刺底部的水平剪切力F1和F2計算公式為

（6）

（7）

式中：C為土壤粘聚力；φ為土壤內摩擦角；η為履帶板剪切速度系數，假設取1.

當履帶板運動時，履刺受到車輛的重力作用完全壓入土里.車輛的垂直載荷由履刺和履帶板共同承擔.

當車輛行駛時，作用在履刺上的法向壓力主要分為兩個部分，一部分是由土的自重引起的法向壓力，另一部分是由粘聚力C所導致的土壓力.土壓力隨著深度的變化不斷增加，作用在履刺上的土壓力如圖6所示.

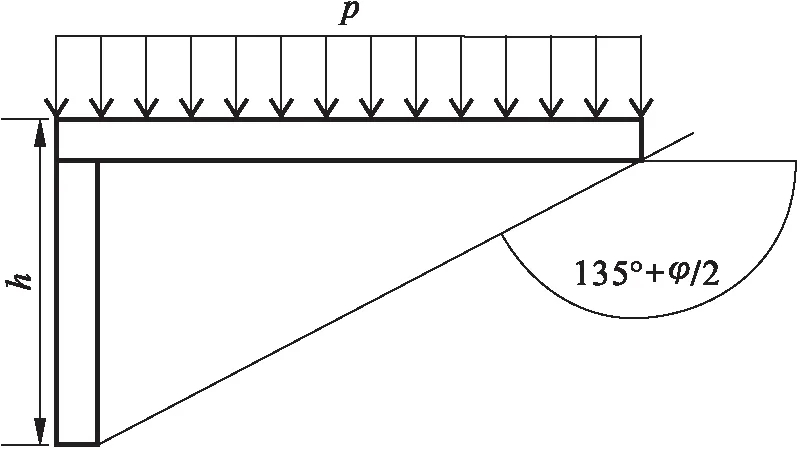
圖6 均布載荷作用下土壤破壞模型Fig.6 Soil failure model under uniform load

考慮到履帶板有一定的接地壓力，使得土壤具有一定的均布載荷.土壤作用在履刺上的水平推力為

（8）

式中：γ為土壤容重；κp為被動土壓力系數；P為均布載荷；I為嚙合區域長度.

土壤對倒三角傾斜部分的額外推力為

F32=chb3tanα

（9）

式中，α為履刺的拔摸角度.則作用在履帶板上的水平推力F3為

F3=F31+14F32

（10）

作用在履刺和履帶板兩側的力F4可以通過彈性力學理論進行計算，即

（11）

因此，履帶板在行駛過程中所受到的合力為

FH=F1+F2+F3+F4

（12）

以LF1352森林運載車為例，表1為履帶板結構參數和土壤力學性能表.

3 積雪和履帶板的仿真實驗分析

當履帶板受到垂直載荷時，積雪處于彈性階段，考慮到本文中的履帶車輛載荷為26 kPa，雪的變形分為兩個區域：第一個區域為彈性區域，隨著壓力逐漸接近雪的粘聚力，積雪發生彈性形變，該區域通常來說比較小；第二個區域為材料塑性變形區，如果雪有足夠的深度，接地壓力會一直傳遞到雪的底部.在計算過程中，積雪被假設為連續體，把積雪視為一種固體材料.為了研究履帶板在雪的剪切過程中受到的剪切力，運用有限元軟件建立積雪彈塑性本構模型.

表1 履帶板結構參數和土壤力學性能Tab.1 Structure parameters of track shoes and mechanical properties of soil

3.1 單條履帶板仿真分析

在仿真過程中將履帶板的運動簡化為沉陷和水平剪切兩個部分.當履帶板運動時，在履帶板頂部添加載荷來模擬接地比壓，再給履帶板施加一個沿Y軸正方向的水平位移來模擬履帶板的水平剪切運動.由于履帶板在雪中運動是一個非線性、大位移的過程，可通過動態顯式分析方法對其進行分析.動態顯式方法通過在分析過程中不斷重新劃分網格來求解，可以不斷改變網格質量，有效解決分析過程中的網格畸變問題.考慮到履帶板的材料屬性為鋼，在運動過程中基本不變形，為了減少計算時間，將履帶板設置為剛體，并對履帶板與雪模型接觸的部分進行網格加密以保證計算數值的準確性.履帶板運動分析過程中將履帶板模型簡化為寬度為570 mm、履帶板節距為155 mm、履刺高度為30 mm、拔模角度為60°的履帶板，如圖7所示.

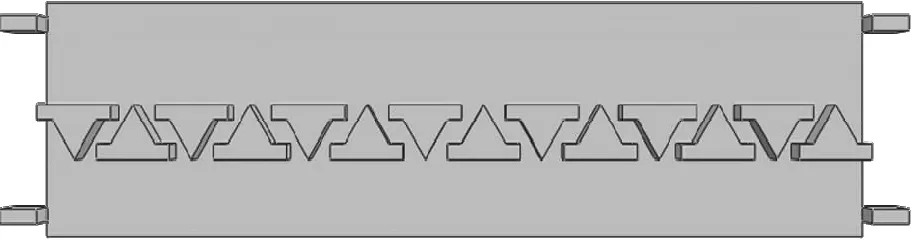
圖7 履帶板模型Fig.7 Track shoes model

將雪的三維模型簡化為彈性模型和Mohr-Coulomb塑性模型.雪模型的面積超過履帶板兩倍尺寸外的部分基本沒有變形，因此積雪模型尺寸為長1 500 mm、寬1 500 mm、高500 mm，相關參數見表1.將履帶板放置在雪模型上，限制雪四周的自由度，在第一個分析步給履帶板添加接地比壓讓履帶沉陷，在第二個分析步給履帶添加Y軸正方向50 mm位移，讓履帶板在積雪模型上水平剪切，加密模型如圖8所示.

圖8 仿真實驗網格圖Fig.8 Simulation experiment meshing

輸出變量是履帶板在運動過程中所受到的水平方向反作用力之和，即履帶板受到的剪切力.在仿真結束時，履帶板前方的積雪不斷堆積在一起，正下方形成一個空腔，如圖9所示，與實際情況基本一致.

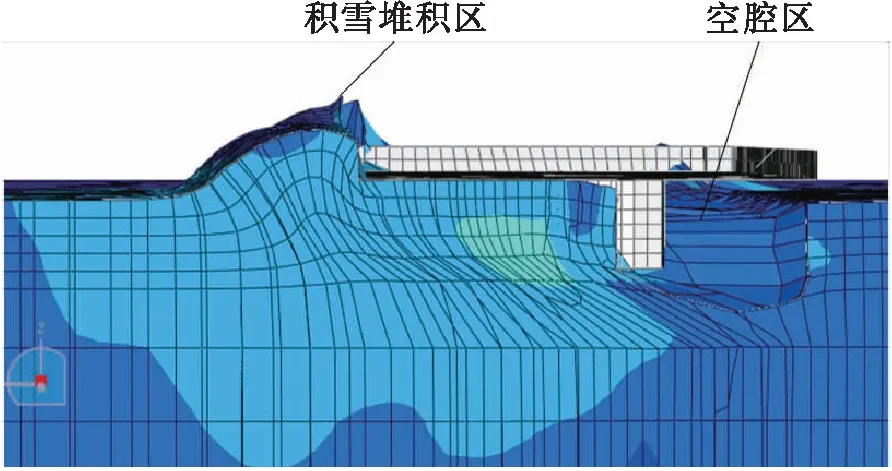
圖9 積雪受力圖Fig.9 Force diagram of snow

為了計算車輛在積雪路面上行駛的牽引力，選用壓實積雪的力學性能參數，計算出單塊履帶板受到的剪切力計算值約為3 600 N.

為了驗證有限元分析的可靠性，將仿真結果與公式計算結果進行對比分析，結果如圖10所示.履帶板受到的剪切力在較小位移時快速上升到達頂點，仿真剪切力要稍小于計算剪切力，可以認定仿真有效.

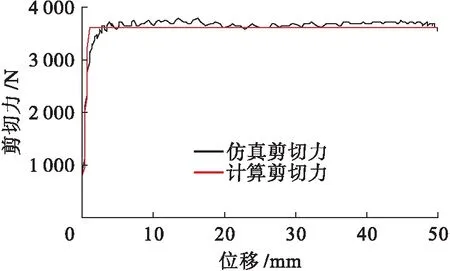
圖10 仿真數值與計算結果對比Fig.10 Comparison between simulation values and calculation results

3.2 多條履帶板仿真分析

為了研究履帶板受到的剪切力與履帶板花紋數量的關系，對不同數量履帶板進行仿真分析.選用履刺高度為30 mm、履帶板節距為155 mm、拔模角度為60°的履帶板數據，實驗輸出結果為履帶板受到的全部反力.以兩塊履帶板為例，結構如圖11所示.

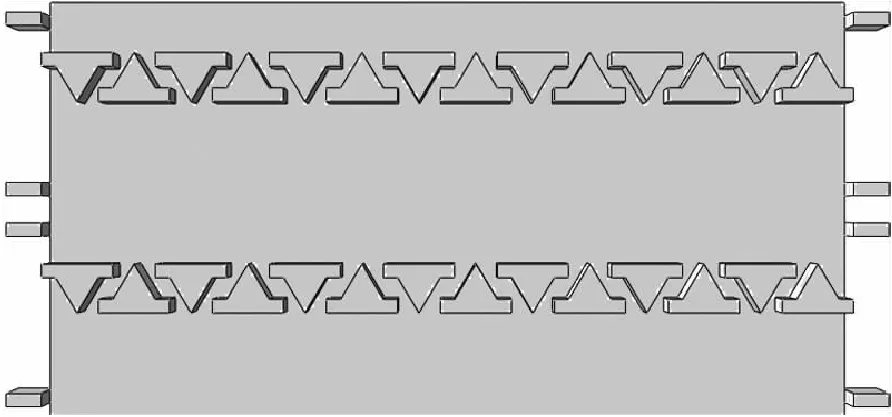
圖11 雙排履帶板Fig.11 Double row track shoes

將多排履帶板的數據進行整理，結果如圖12所示.

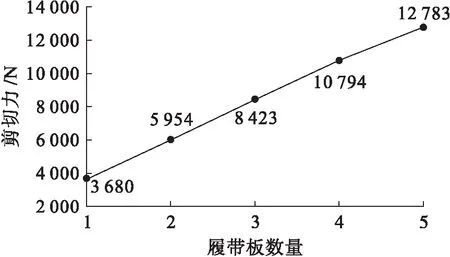
圖12 履帶板數量剪切力折線圖Fig.12 Number of track shoes-shear force line chart

由圖12可知，隨著履帶板數量的增加，剪切力也隨之增加，增幅約為60%.因此整車的受力為

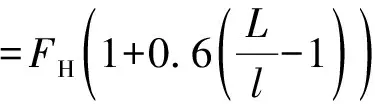
（13）

4 履帶板優化設計

4.1 履刺花紋擠壓區域面積對剪切力的影響

履帶板的設計參數對剪切力有很大影響，為了探究擠壓區域面積對履帶板剪切力的影響，選用履刺高度為30 mm、履刺節距為155 mm、履刺角度為60°的無嚙合區域履帶板模型.圖13為單因素試驗結果.由于增加履帶板水平距離會令擠壓區域變形，失去擠壓能力，因此選擇增加成對履帶花紋之間的縱向距離來增大擠壓區域.履刺角度β為

β=π-2α

（14）

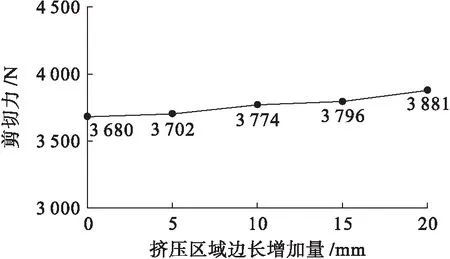
圖13 單因素實驗結果Fig.13 Single factor test results

由圖13可知，當履帶花紋的垂直距離增加時，履帶板受到的剪切力的變化幅度很小，擠壓區域的面積大小對履帶板受到的剪切力影響較小.

4.2 履帶板節距、履刺高度、履刺角度對履帶板剪切力的影響

為了研究不同履帶板設計參數對于履帶在積雪路面時受到的剪切力的影響，考察的因素有履帶板的履刺高度、履帶板節距、履刺角度，將剪切力作為考察指標.本實驗采用Box-Behnken進行分析，將考察因素作為自變量，將剪切力作為響應值.確定的因素水平如表2～3所示.

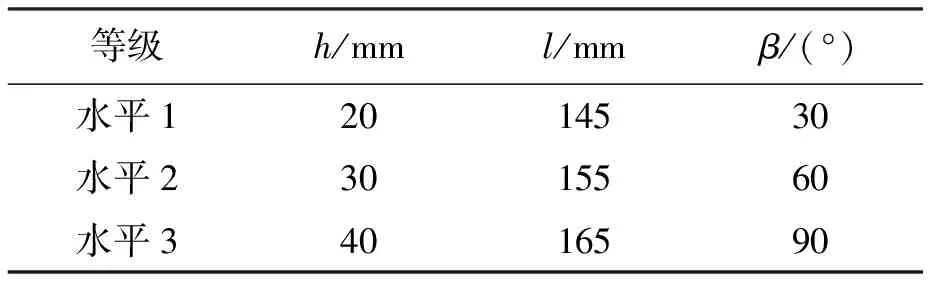
表2 Box-Behnken實驗因素水平Tab.2 Box-Behnken test factor levels

對實驗進行方差分析，結果如表4所示.由方差分析可知，履刺高度、節距對剪切力的影響最為顯著，履帶板的拔模角度對履帶板的剪切力影響較小.圖14為Box-Behnken實驗響應圖.將顯著性因素作為自變量，剪切力作為響應值，隨著履刺節距和履刺高度的增加，履帶的剪切力也不斷增加，履帶板受到的剪切力與履刺高度、履帶板節距呈正相關.

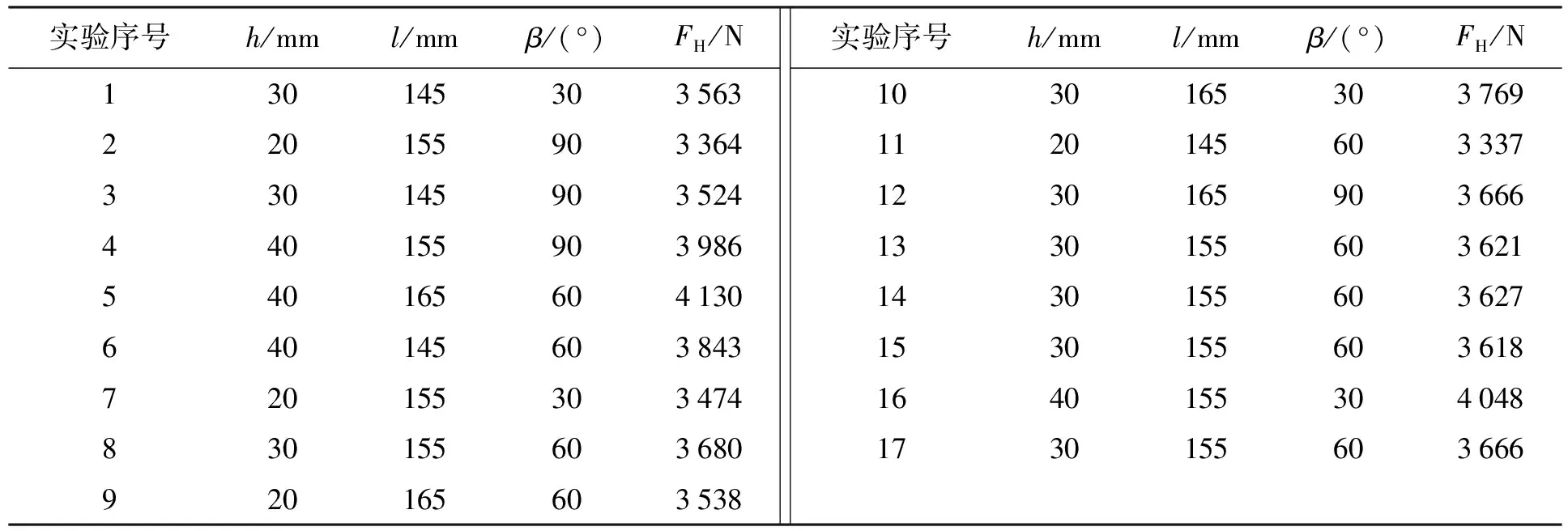
表3 Box-Behnken實驗結果Tab.3 Box-Behnken test results

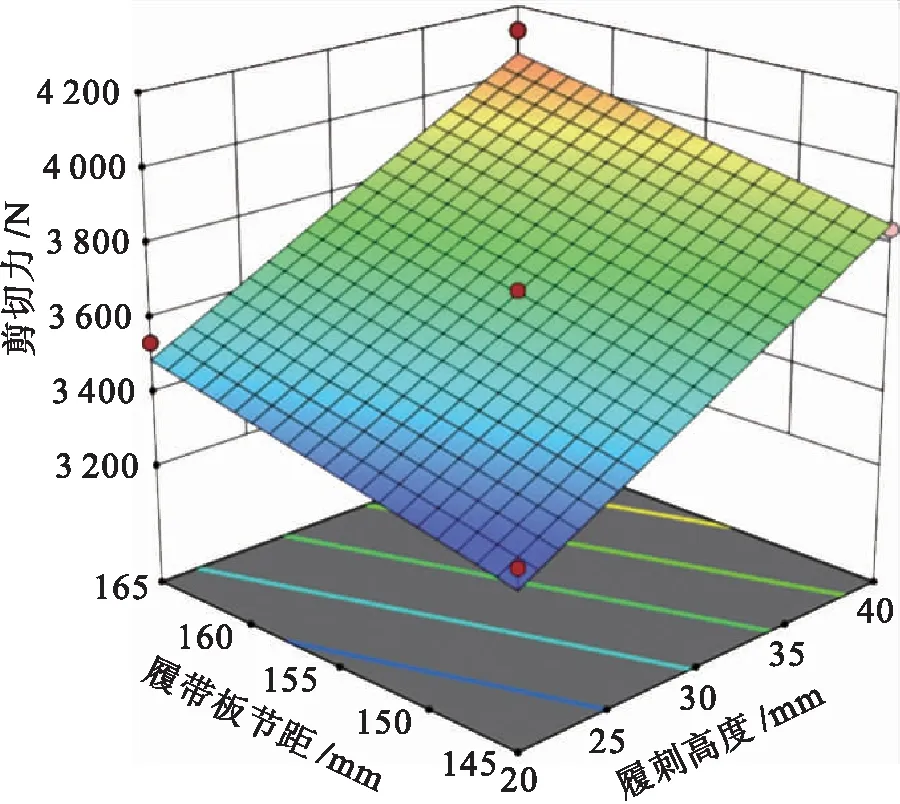
圖14 Box-Behnken實驗響應Fig.14 Box-Behnken test response

4.3 履帶板設計參數優化

考慮到履帶板尺寸參數的增大會造成車輛行駛噪音大、動載沖擊強、轉向困難等問題，對履帶板的設計參數進行優化，優化目標為在符合通過性的前提下盡量減小履帶板的尺寸參數.優化對象參數選擇履帶板節距和履刺高度，約束條件選擇LF1352森林運載車在林區的爬坡能力.履帶板節距的最小值為145 mm，履刺高度的最小值為0 mm.

優化的目標函數為履帶板體積的最小值，即

（15）

約束條件為：

1） LF1352森林運載車能通過45°的坡面角度，約束函數為

W（ξ+sin 45°）≤2F總

（16）

式中，ξ為履帶板的阻力系數，本文取0.2.

2） 本文中垂直于履刺剪切面的力的計算公式基于Rankine被動土壓力理論，即

（17）

優化結果如表5所示.

表5 優化結果Tab.5 Optimization results

5 結 論

2） 通過研究履帶板因素對剪切力的影響，得出履刺高度和履帶板節距對剪切力的影響較為顯著，并呈正相關.剪切力隨著履帶板節距、履刺高度的增加而增大.拔模角度、擠壓區域面積對剪切力影響較小.

3） 得出了履帶車輛在積雪路面上整條履帶板與單一履帶板的受力關系，推導出了整條履帶板的剪切力計算公式，并對履帶板的結構尺寸進行了優化.