一道新高考導數壓軸題的分析與延伸
雷 蕾 (江蘇省南京市第一中學 210001)
2022年新高考I卷第22題是一道函數與導數綜合的壓軸題,考查了利用導數研究函數的極值與最值、零點等知識,體現了分類討論、數形結合、函數與方程、轉化與化歸等數學思想,對學生的邏輯推理、直觀想象、數學運算等核心素養要求較高.下面筆者從分析高考真題、推廣一般結論、探究其他性質這三個方面展開,對這道壓軸題進行深度解析,供大家參考.
1 分析高考真題,厘清解題思路
試題(2022年新高考I卷第22題)已知函數f(x)=ex-ax和g(x)=ax-lnx有相同的最小值.
(1)求a;(2)證明:存在直線y=b,其與兩條曲線y=f(x)和y=g(x)有三個不同的交點,并且從左到右的三個交點的橫坐標成等差數列.
思路 (1)分2步:①分別求出f(x)與g(x)的最小值(用a表示),由f(x)與g(x)的最小值相等建立關于a的方程;②利用導數求解關于a的方程.
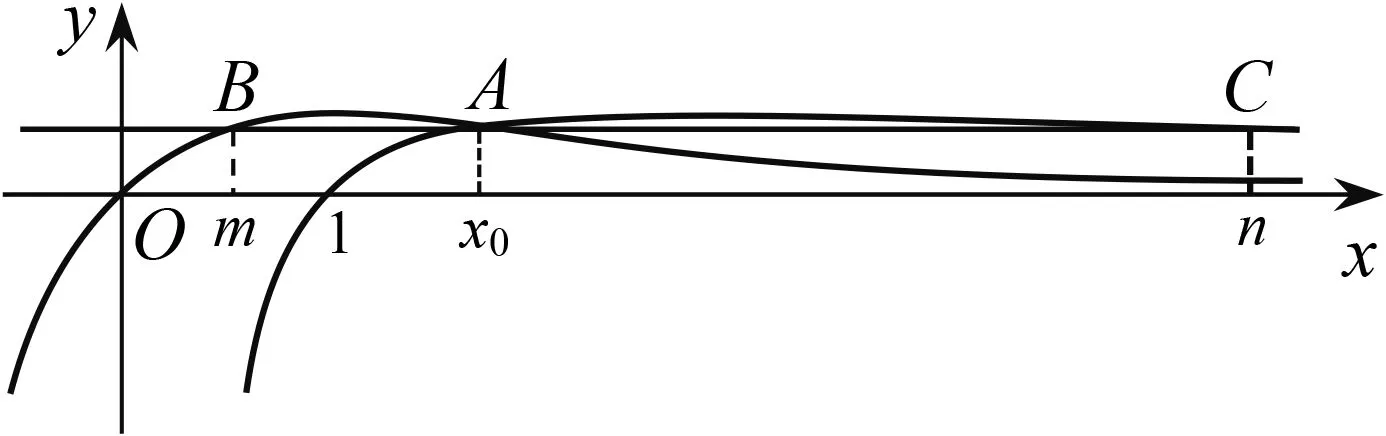
(2)分3步:①證明f(x)與g(x)的圖象只有一個交點(x0,y0);②證明直線y=y0與f(x),g(x)的圖象各有另一個交點;③證明從左到右的三個交點的橫坐標成等差數列.
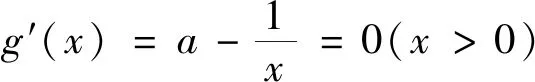
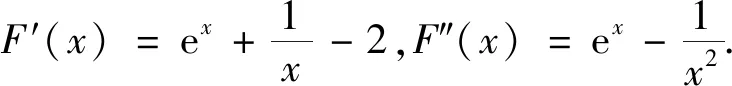
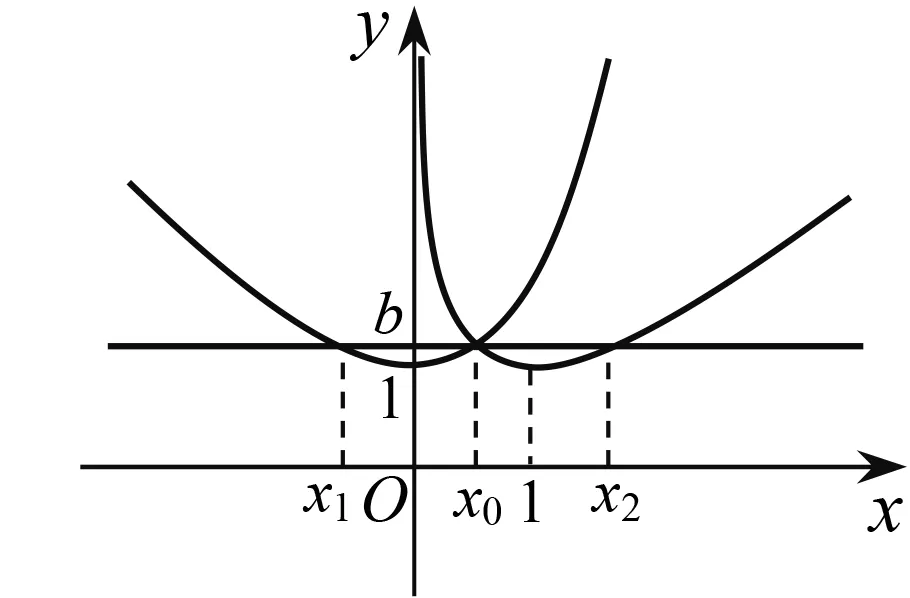
圖1
因為f(lnx0)=x0-lnx0=ex0-x0=f(x0),由f(x)的單調性可知,直線y=b與f(x)的圖象交于兩點(lnx0,b),(x0,b).因為g(ex0)=ex0-x0=x0-lnx0=g(x0),由g(x)的單調性可知,直線y=b與g(x)的圖象交于兩點(x0,b),(ex0,b),所以存在直線y=b與f(x),g(x)的圖象有三個交點,其橫坐標從左到右依次為lnx0,x0,ex0.由ex0-x0=x0-lnx0知,其橫坐標成等差數列.

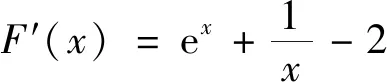
2 探究其他情況,得出一般結論
從上述分析可以發現,本題的第(2)題就是從直線y=b經過f(x)與g(x)圖象的交點出發進行命制,考查了一種特殊情形.那么,對于一般情況,也就是直線y=b不經過f(x)與g(x)圖象的交點時,是否有類似的結論?
變式1 已知直線y=b與f(x)=ex-x和g(x)=x-lnx的圖象共有四個不同的交點.
(1)求實數b的取值范圍;
(2)設這四個交點的橫坐標從左到右依次為x1,x2,x3,x4,求證:x1+x4=x2+x3.
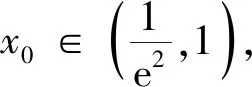
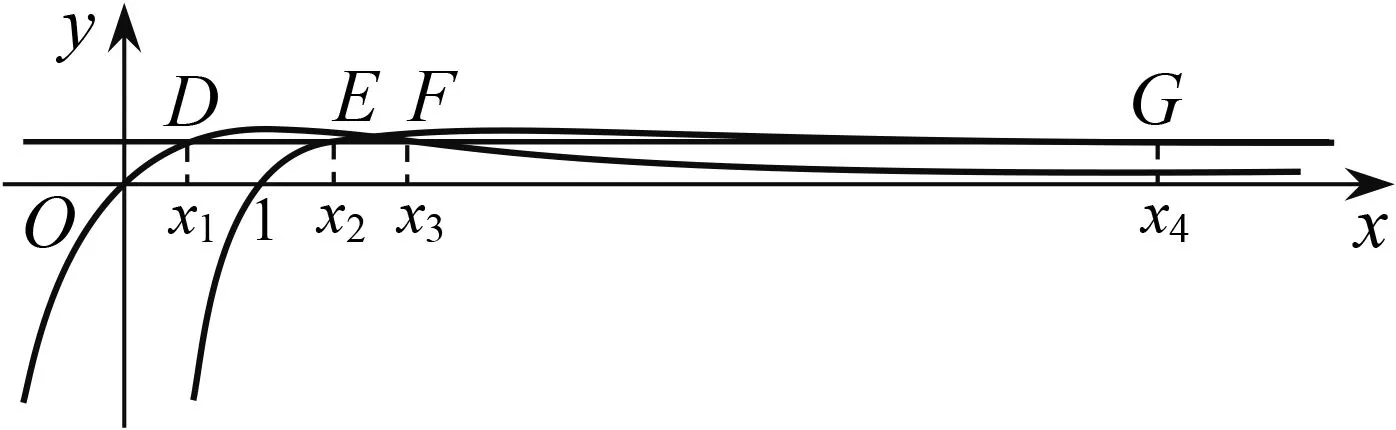
(2)①由(1)知,當b∈(1,y0)時,直線y=b與f(x)圖象交點的橫坐標從左到右依次為x1,x2,直線y=b與g(x)圖象交點的橫坐標從左到右依次為x3,x4,即f(x1)=f(x2)=g(x3)=g(x4)=b,其中lnx0 圖2 圖3 ②由(1)知,當b∈(y0,+∞)時,直線y=b與f(x)圖象交點的橫坐標從左到右依次為x1,x3,直線y=b與g(x)圖象交點的橫坐標從左到右依次為x2,x4,即f(x1)=g(x2)=f(x3)=g(x4)=b,其中x1 綜上,x1+x4=x2+x3. 評注(1)對于變式1第(1)題中的交點個數問題,也可以用零點存在定理進行判斷: (2)若將試題與變式1中的函數一般化,即f(x)=ax-x,g(x)=x-logax,其中a>1,容易判斷f(x)與g(x)都只有一個極小值點,且極小值相等.利用f(logax)=g(x)與g(ax)=f(x)可以證明: ①若直線y=b與兩條曲線y=f(x)和y=g(x)共有三個不同的交點,則從左到右的三個交點的橫坐標成等差數列; ②若直線y=b與兩條曲線y=f(x)和y=g(x)共有四個不同的交點,設這四個交點的橫坐標從左到右依次為x1,x2,x3,x4,則x1+x4=x2+x3. 通過對試題與變式1的分析,我們發現函數f(x)與g(x)之所以具有上述性質,關鍵是滿足兩點:①f(logax)=g(x),g(ax)=f(x);②f(x)與g(x)都只有一個極值點,且極值相等. 下面筆者適當改變f(x)與g(x)的解析式,使其滿足上述兩個關鍵點,探究其他函數的類似性質. (1)若直線y=b與兩條曲線y=f(x)和y=g(x)共有三個不同的交點,試探究:從左到右三個交點的橫坐標之間的關系; (2)若直線y=b與兩條曲線y=f(x)和y=g(x)共有四個不同的交點,試探究:從左到右四個交點的橫坐標之間的關系. 圖4 圖5 綜上,若直線y=b與兩條曲線y=f(x)和y=g(x)共有四個不同的交點,設從左到右四個交點的橫坐標分別為x1,x2,x3,x4,則x1x4=x2x3. ②當x∈(e,+∞)時,lnx>1,因為f(x)在(1,+∞)上遞減,易證x>lnx,所以f(x) ①若直線y=b與兩條曲線y=f(x)和y=g(x)共有三個不同的交點,則從左到右三個交點的橫坐標成等比數列; ②若直線y=b與兩條曲線y=f(x)和y=g(x)共有四個不同的交點,設這四個交點的橫坐標從左到右依次為x1,x2,x3,x4,則x1x4=x2x3. 總之,對于一道典型的高考真題,我們不能僅僅局限于解決這個問題,還應從多個角度對其進行剖析,充分挖掘其價值.通常可以思考如下問題:你能用多種方法求解這個問題嗎?這個問題的命題意圖是什么?改變條件或目標后這些方法還適用嗎?這個問題能否推廣到一般情形?等等.只有真正弄清這個問題的來龍去脈,把握其各種變化,我們在遇到新問題時才能做到靈活處理、巧妙應對.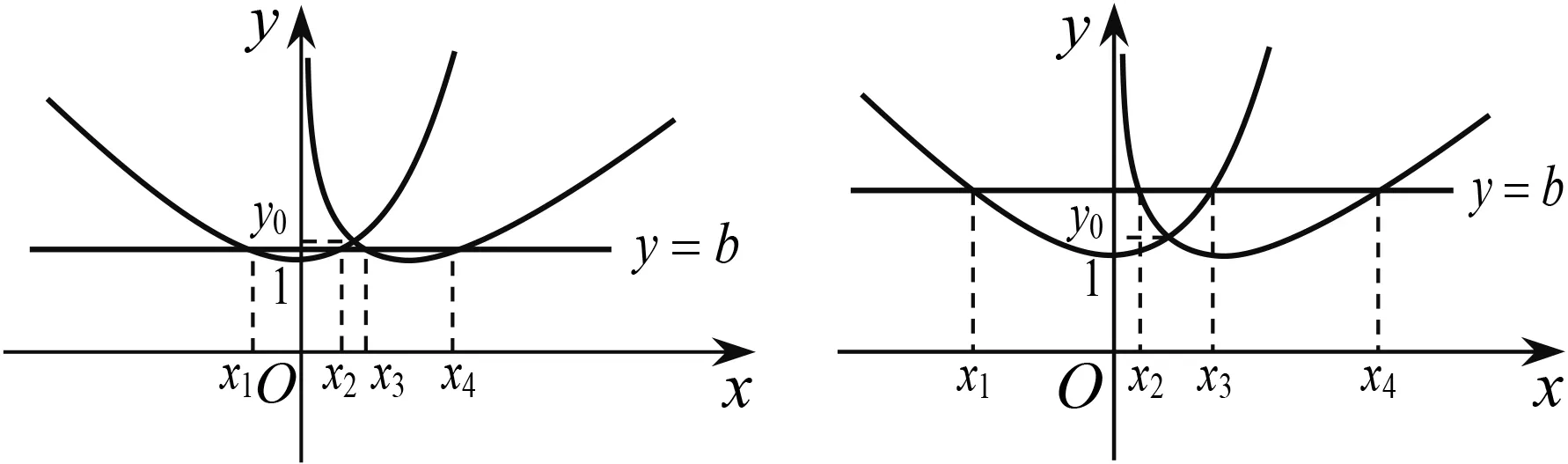
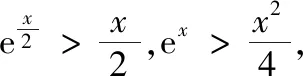
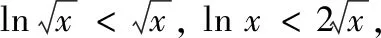
3 總結命題規律,探究其他性質
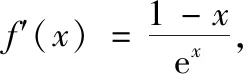
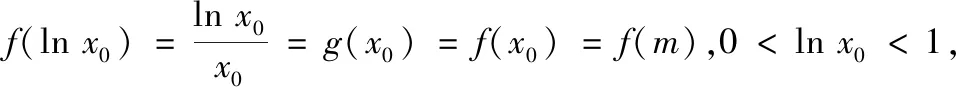
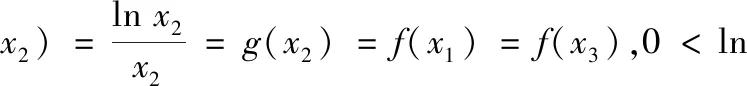
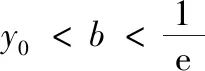
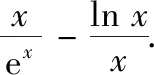


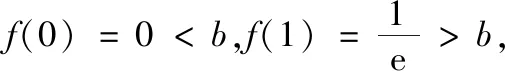

4 結語

