Python在概率論與數理統計教學中的應用案例研究

王永娟 姜喜春 謝兵兵

(黑河學院 理學院，黑龍江 黑河 164300)

隨著科學技術的發展和社會現代化的推進，社會對大數據科學的研究與應用型人才的需求與日俱增。概率論與數理統計是統計學和數據挖掘的理論基礎，在大數據專業中顯得尤為重要。大數據的價值體現在其蘊含的規律，對數據處理、分析離不開統計學和數據挖掘，而其原理和方法基于概率論與數理統計。Python軟件作為大數據分析的主流軟件，具有簡潔、可讀性強、易于操作等特點，是每個大數據專業學生必須掌握的軟件之一。那如何將Python軟件引入到概率論與數理統計的教學過程中，使學生既理解了概率論與數理統計的理論，又掌握了Python軟件的應用呢？本文從三個方面探討Python在概率論與數理統計教學中的應用案例，旨在激發學生的學習積極性，提高課堂教學質量，為培養大數據人才提供一定的參考。

一、Python在f分布圖像上的應用

定義[1]：設且X與Y相互獨立，稱隨機變量

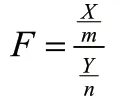
的分布為具有(m,n)的F分布，記F～F(m,n)

自由度為(m,n)的F分布的概率密度函數為

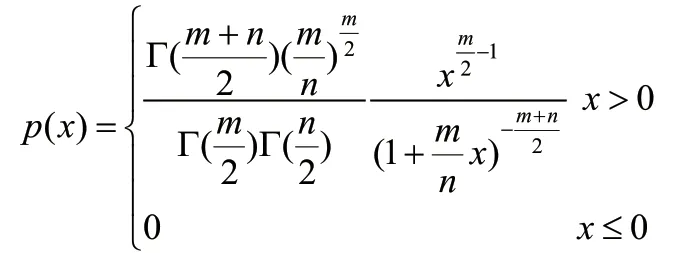
在教學過程中發現，F分布的概率密度函數比較抽象，學生理解起來比較困難，所以利用python軟件畫出不同自由度下F分布的圖像[2]，如圖1所示，幫助學生掌握F分布中兩個自由度對函數圖像的影響。

從圖1可以看出，F分布圖像是非對稱分布，自由度m和n是有順序的，不同的自由度圖像的偏度不同。同時，將代碼展示給學生，加深對Python中scipy庫內F分布概率密度函數f.pdf()的以及matplotlib庫內繪圖函數的使用，圖像上顯示中文、負數等方法的理解。

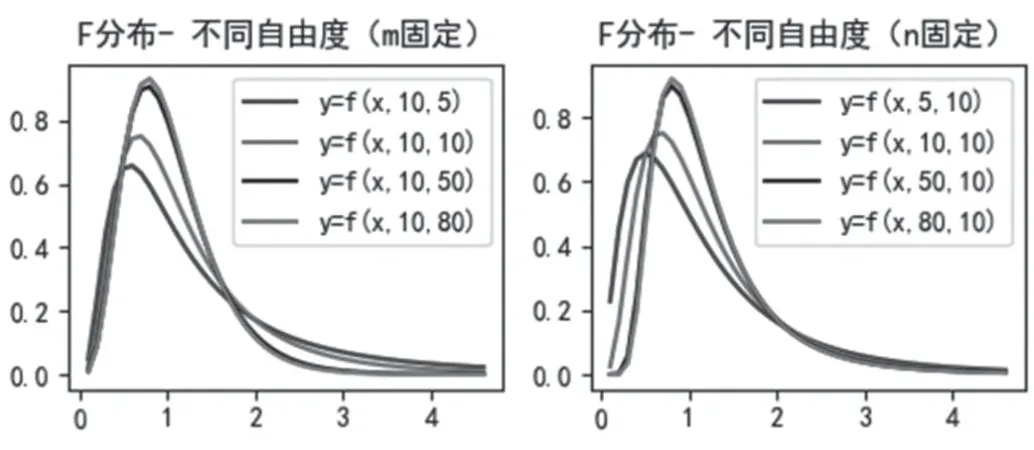
圖1 F分布圖像

二、Python在點估計中的應用

在概率論與數理統計中點估計有兩種常見的方法：矩估計法和極大似然估計法，在理解兩種方法原理的情況下，應用原理進行推導計算，得到公式帶入數據進行計算計算，過程相對復雜[3]。對于大數據專業的學生，因為已經有一定的python基礎，可以應用python軟件進行計算。

程序中蘊含矩估計表達式，結合相應函數，程序本身也能加深對矩估計法的理解，同時學生在遇到類似的問題，只需要把原始數據替換，即可求得相應的矩估計值，簡化計算。

三、Python在區間估計中的應用

以正態總體均值的區間估計為例，在總體方差已知和未知兩種情況下分別進行討論，相比較帶公式計算，用python代碼運行更加簡便。

1.總體標準差已知情況下

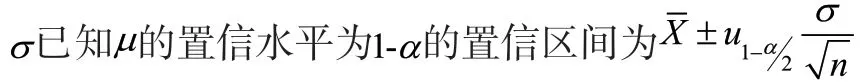
例2：20世紀末，某高校對50名大學生的午餐費進行調查，得到樣本均值為3.10元，假設總體的標準差為1.75元，是求總體均值(即該校大學生的平均午餐費)的0.95的置信區間。

代入公式即可求得置信區間，調用python運行如下[4]：

2.總體標準差未知情況下(小樣本)

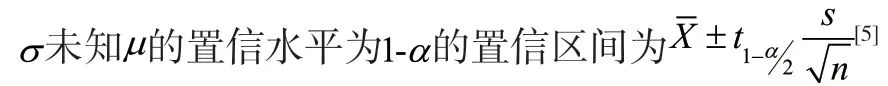
例3：2005年某市某行業職工的月收入服從N(μσ2)，現隨機抽取30名職工進行調查，求得他們的月收入的平均值2084元，標準差元，試求的置信水平為0.95的置信區間。

代入公式即可求得置信區間，調用python運行如下：

3.置信區間圖像

在給定均值和方差的條件下，利用np.random.normal()函數生成服從正態分布數據，利用st.t.interval()計算出置信區間[6]，并畫出圖形如圖2所示。

圖2 正態均值置信區間

從圖像中可以清晰看出，正態數據與置信區間的包含關系，幫助學生理解置信區間的含義。

四、結語

概率論與數理統計中的一些定理與大數據專業中的軟件相結合[7]，不但可以提高運算速度，更重要的是可以生動形象地演示復雜定理的變化過程，揭示其內在規律，從而激發學生的學習興趣。Python語言是數據科學與大數據技術領域主要應用語言之一，因為Python在處理大量數據時具有高效率、自動化、可運用算法建立數據模型等特點，是大數據專業的學生必備語言，在概率論與數理統計教學過程中運用python軟件可以起到事半功倍的效果。