商科院校本科畢業生創業行為選擇的演化博弈分析
任嬋媛,焦晉鵬
(哈爾濱商業大學 校團委, 黑龍江 哈爾濱 150076)
一、引言
面對當前日趨嚴峻的國內外經濟發展形勢,國家出臺了大力推進大眾創業、萬眾創新的支持政策,提出了“眾創、眾包、眾扶、眾籌”等新模式,并通過“十三五”期間深入推進“鼓勵以創業帶動就業,建立面向人人的創業服務平臺”等就業政策的實施,以及“十四五”規劃中提出的“完善促進創業帶動就業、多渠道靈活就業的保障制度”,有效解決了經濟體制改革與產業結構調整過程中出現的部分群體就業難的問題,保障了社會總體就業水平的穩定。
作為當前供需匹配錯位較為嚴重的就業群體,高校商科院校本科畢業生就業難問題近年來愈加突出,如何實現以創業帶動就業已成為解決商科院校本科畢業生就業難問題的關注焦點。本研究嘗試運用演化博弈理論分析高校本科畢業生創業行為選擇過程中兩個博弈主體之間的演化穩定策略,在此基礎上找到影響創業行為選擇的關鍵因素,從而進一步完善高校支持商科院校本科畢業生創業的保障體系,切實推進“雙創”工作的開展。
二、創業行為選擇過程中高校與商科院校本科畢業生之間靜態博弈分析
(一)博弈的前提假設
1.假設創業行為選擇過程中存在兩類行為主體:高校與商科院校本科畢業生,構成博弈方組合B={1,2},其中參與人1 為高校,參與人2 為本科畢業生,兩類行為主體都是完全理性的,即在給定的條件下,做出的決策都是使自己期望效用最大化。
2.假設在創業行為選擇過程中的兩類主體都存在兩種行為策略,即高校的策略集為E={支持,不支持},支持是指高校鼓勵商科院校本科畢業生創業,開展創業教育并根據規定為創業學生提供政策和資金支持,不支持則是高校不提供創業教育、投資資金等資源。商科院校本科畢業生的策略集為E={創業,不創業},一般來說,商科院校本科畢業生會根據求職獲得崗位的滿意程度及創業意愿選擇自身策略行為。
3.在不考慮雙方行動順序的情況下,高校與商科院校本科畢業生的博弈結果矩陣如下:
當商科院校本科畢業生選擇創業,并取得成功時;

圖1 創業成功情況下高校與商科院校本科畢業生完全信息靜態博弈矩陣
當商科院校本科畢業生選擇創業,但創業項目未能成功孵化時;

圖2 創業項目未能孵化情況下高校與商科院校本科畢業生完全信息靜態博弈矩陣
其中C表示高校支持商科院校本科畢業生創業所投入的成本;C表示表示商科院校本科畢業生創業所投入的成本,包括資金、時間、精力等各類成本;W表示商科院校本科畢業生在企事業單位工作所取得的預期收益;W表示商科院校本科畢業生進行創業成功時所獲得的預期收益(W>W;W>C);I 表示商科院校本科畢業生創業所獲得的高校提供的專家咨詢、啟動資金等培養計劃外的資源支持;R 表示高校支持商科院校本科畢業生創業時地方政府給予的補貼;V 表示商科院校本科畢業生創業成功為學校帶來良好聲譽,進而吸引更多的生源,實現的增加收益;P 表示商科院校本科畢業生接受高校創業教育后未進行創業,沒能有效響應國家“雙創”號召,地方政府對高校創業支持補貼的削減,屬于對高校創業支持不力的懲罰。
(二)商科院校本科畢業生創業行為的博弈分析
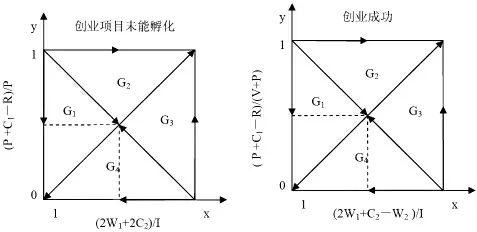
根據博弈模型的前提假設及博弈分析收益矩陣,對靜態博弈條件下的博弈雙方的收益情況進行分析,具體情況如下:在創業取得成功的情況下,且W>2W+C時,商科院校本科畢業生受可觀的創業預期回報吸引,在權衡自身風險承受能力和審視自身創業意愿的情況下,受良好的創業支持條件的驅動,將會選擇創業;而在創業項目不能完成孵化的情況下,僅當I>2W+C時,商科院校本科畢業生才會選擇創業。對于高校來說,高校支持創業支付成本為C,但在此情況下高校會獲得政府給予的補貼R和商科院校本科畢業生創業成功帶來的聲譽效應收益V,若R>C,則高校的最優策略則為支持;若(R+V) 當W+I<2W+C時,商科院校本科畢業生在權衡預期收益的情況下,理性選擇是不創業,規避相應的風險,因為若選擇創業,且未能完成孵化,本科畢業生的損失為(C+W),沒有產出的投入顯然不是理性的決策行為。由于“雙創”對高校的政策和資金支持是先行兌付,當R>C+P時,高校的最優策略為支持,但隨著政府對高校創業支持效果不佳的懲戒式措施逐漸變嚴格,當R 因此,高校支持商科院校本科畢業生進行創業的關鍵在于政府給予的補貼收益能否補償高校的支出成本,當R 根據納什均衡策略的相關定義,一定存在一個混合策略納什均衡,在以上研究的基礎上,建立2×2 雙矩陣博弈模型,假設參與人1 即高校支持商科院校本科畢業生創業的概率為x(0≤x≤1),不支持的概率為1-x;參與人2 即商科院校本科畢業生選擇創業的概率為y(0≤y≤1),不創業的概率為1-y。則此時的博弈模型可以表示為以下形式: 當商科院校本科畢業生選擇創業,并取得成功時; 圖3 混合策略下高校與商科院校本科畢業生間的靜態博弈模型(成功) 因此,高校支持商科院校本科畢業生創業的期望支付成本為 對于高校來說,支持商科院校本科畢業生創業獲得最大收益條件是收益期望函數一階導數等于0,即 對于商科院校本科畢業生來說,其獲得最大收益的條件是收益期望函數一階導數等于0,即 當商科院校本科畢業生選擇創業,但項目未能成功孵化時; 圖4 混合策略下高校與商科院校本科畢業生間的靜態博弈模型(未能孵化) 按照上述計算方法,商科院校本科畢業生選擇創業但項目未能孵化情況下高校與商科院校本科畢業生最大收益概率分別為: y x y y y y y P C R P y y x x x x x W C I x x 在靜態條件下,高校和商科院校本科畢業生之間由于信息的對稱性和雙方的有限理性,可以通過納什均衡[(P+C-R)/(V+P),(2W+C-W)/I]和[(P+C-R)/P,(2W+2C)/I]中變量的變化不斷調整自身的應對策略,但是,在高校與商科院校本科畢業生參與創業行為決策的過程中,博弈雙方信息是非對稱的,各高校和商科院校本科畢業生不同個體間關于創業行為決策的選擇受諸多因素的影響,不可能實現完全的有限理性,雙方會針對創業行為的行為決策不斷的重復博弈。因此,靜態條件下的均衡不能有效體現博弈雙方的演化路徑,動態反映國家“雙創”號召在存在差異的高校和商科院校本科畢業生群體中實際響應效果,需要借助演化博弈分析的方法對該行為選擇進行進一步的探討。 基于靜態博弈分析的前提假設,建立兩總體2×2 行演化博弈模型。由多總體演化博弈的特點可以看出,該演化博弈的演化穩定策略和漸進穩定狀態是等價的,并且一定是純策略納什均衡。假設高校群體中選擇支持商科院校本科畢業生創業的比例為x(0≤x≤1),商科院校本科畢業生群體中選擇創業的比例為y(0≤y≤1)。在高校與商科院校本科畢業生博弈的過程中,雙方決策的適應性如果比群體的平均適應性高,則該決策會成為主導發展方向。因此,該博弈下的復制子動態方程組為: 根據演化博弈理論,上述系統演化路徑與均衡可從以下兩個角度進行分析: 在創業成功的情況下,當y=(P+C-R)/(V+P)時,x"=0;在創業項目未能成功孵化的情況下,當y=(P+C-R)/P 時,x"=0,此時,對于所有的x 概率的高校的決策選擇都是穩定的,具體來說,當商科院校本科畢業生選擇創業決策的比例為(P+C-R)/(V+P)或(P+C-R)/P 時,高校采取支持與不支持商科院校本科畢業生創業的決策所獲得的收益是相等的,兩種行為策略無差異。 在創業成功的情況下,當y≠(P+C-R)/(V+P)時,以及在創業項目未能成功孵化的情況下,當y≠(P+C-R)/P時,x=0 與x=1 時,均可得到x"=0,因此x 取這兩個值時是高校決策選擇的兩個穩定狀態均衡點。此時,對y 的取值情況進行分析,如果y>(P+C-R)/P,則x">0,在此情況下,高校支持創業的收益大于群體的平均水平,因而在x=0 的穩定狀態下,若在國家“雙創”指示的號召下,積極鼓勵并支持商科院校本科畢業生創業的高校取得了好的效果,未行動的高校將進行效仿,相繼采取支持創業的決策,即x=1 是復制動態下的一個演化穩定策略,也是高校的最優選擇;如果y<(P+C1-R)/(V+P),則x"<0,在此情況下,高校選擇支持商科院校本科畢業生創業的決策所取得的收益低于群體的平均水平,因而在x=1 的穩定狀態下,部分高校經過嘗試而最終放棄支持商科院校本科畢業生創業,那么存在相同情況的其他高校也會相繼采取相同的決策,即x=0 也是復制動態下的一個演化穩定策略,但從國家為解決就業問題,響應“雙創”號召的角度來看,該決策行為屬于消極策略,應予以通報。 因此,y=(P+C-R)/(V+P)(創業成功) 及y=(P+C-R)/P(創業項目未能成功孵化)是x=0 和x=1 兩類演化策略的分界點,高校支持商科院校本科畢業生創業投入的成本、支持創業獲得的補貼及地方政府對高校支持創業效果不佳的補貼削減是影響高校決策的重要影響因素。 在創業成功的情況下,當x=(2W+C-W)/I 時,y"=0;在創業項目未能成功孵化的情況下,當x=(2W+2C)/I 時,y"=0,此時,對處于y 值概率的商科院校本科畢業生來說選擇創業與不創業的行為決策都是穩定的。具體來說,兩種情況下高校采取支持商科院校本科畢業生創業的比例分別為(2W+C-W)/I 和(2W+2C)/I 時,選擇創業與不創業的本科畢業生數量是隨機的。 在創業成功的情況下,當x≠(2W+C-W)/I 時,以及在創業項目未能成功孵化的情況下,當x≠(2W+2C)/I時,y=0 與y=1 時,均可得到y"=0,因此y=0 與y=1 是商科院校本科畢業生選擇的穩定狀態。此時,對x 的取值進行分析,若x>(2W+C-W)/I,則y">0,商科院校本科畢業生選擇創業的收益會大于群體收益的平均水平,所以y=1是復制動態下的一個穩定演化策略,具體來說,當高校支持商科院校本科畢業生創業的比例超過(2W+C-W)/I時,商科院校本科畢業生在了解多數高校支持下的創業者成功了取得了較大的回報收益,失敗了也能獲得相應的損失補償,逐漸趨向選擇創業的決策,并且不會因一部分本科畢業生對創業無動于衷而改變自身最優決策的選擇。若x<(2W+2C)/I,則y"<0,在此種情況下,商科院校本科畢業生選擇創業的收益低于群體收益的平均水平,此時y=0 是復制動態下的一個穩定演化策略,具體來說,當高校支持創業的比例低于(2W+2C)/I 時,商科院校本科畢業生會因大多數高校不支持創業者而放棄創業。 所以,x=(2W+C-W)/I (創業成功) 及x=(2W+2C)/I(創業項目未能成功孵化)是兩類演化穩定策略y=0 與y=1 的分界點,商科院校本科畢業生創業的收益越高,回報越有保障,其選擇創業的行為決策意愿越高,而地方政府對高校創業的政策支持力度越大,給予相應的補貼越高,高校支持商科院校本科畢業生創業的積極性越高,更好的響應國家“雙創”號召。 基于上述對高校與商科院校本科畢業生復制動態方程的分析,可以將博弈雙方的演化復制動態關系以更為直觀的演化路徑圖進行描述。從圖5 可以看出,博弈雙方動態演化最終趨向于哪種均衡取決于博弈初始時模型中變量的取值。如果變量的初始取值在G和G區域內,則通過動態演化博弈最終會穩定于(不支持,不創業)的狀態;如果變量的初始取值在G和G區域內,則通過演化博弈最終將穩定于(支持,創業)的狀態。顯然,在國家“雙創”的號召下,第二種演化方向為理想狀態,即高校在獲得地方政府創業政策支持及補貼后積極引導和支持商科院校本科畢業生創業,而商科院校本科畢業生則在外部創業支持條件的保障下,充分發揮自身的能動性選擇創業,雖然創業存在失敗的風險,但在諸多保障因素的正向強化下,創業意愿依然強烈,而這種結果也是高校、本科畢業生、地方政府之間正向效益最大化的最佳選擇。但是,在現實情況下,由于博弈雙方信息的不對稱性,商科院校本科畢業生的創業行為決策可能仍將理性的以自身條件作為首要考慮因素,并且創業意愿的強烈程度會導致自身行為的非理性決策,同時,商科院校本科畢業生對進入企事業單位工作與創業之間預期收益高低、穩定性和可持續性的衡量比較,也會直接影響創業決策,而風險偏好低的商科院校本科畢業生通常都會采取保守策略,不愿作為創業風險的主要承擔者。高校對于商科院校本科畢業生創業行為的決策,同樣是對支持商科院校本科畢業生創業的投入與收益之間進行比較的結果,若不能獲取預期的收益,高校同樣會降低對商科院校本科畢業生創業的支持力度,進而流于形式。 圖5 高校與商科院校本科畢業生演化博弈分析路徑圖 基于上述的分析可知,高校商科院校本科畢業生自身創業意愿、創業風險偏好程度及外部支持條件均直接影響著最終行為的選擇,而高校雖然同樣注重收益與成本的對比分析,但在意愿上卻明顯趨向支持商科院校本科畢業生創業,但是從創業行為的主導者角度來看,若商科院校本科畢業生沒有創業意愿,不進行創業,高校的支持就毫無意義,因此,高校、地方政府必須采取有效措施提高商科院校本科畢業生的創業積極性。 高校要建立并不斷完善創業教育體系。在商科院校本科畢業生創業行為選擇過程中,高校支持商科院校本科畢業生創業首先應從激發商科院校本科畢業生的創業熱情和提高其創業能力入手,只有學生自身有了創業意愿和能力,為創業提供的政策和資金支持才具有著力點,因此,高校必須立足于教育本身,建立起針對大學生的創業教育體系,做好創業課程的設計和師資配備,使創業者學會把握創業機會、選擇和評估創業項目、撰寫創業計劃書、獲取和整合創業資源的能力。在創業課程設計方面,突出高校創業教育的特色,融合管理、經濟、金融、財會、心理學等各類學科的精髓,提升大學生的綜合素質;在師資配備方面,充分整合校內外優秀師資力量,聘請本地的企業家,尤其是畢業后創業成功的企業家與學生交流經驗;而在創業實踐方面,高校要積極組織并參加創業競賽,如管理案例分析大賽、沙盤模擬等,有創業孵化園的學校,可以為商科院校本科畢業生提供全方位的創業孵化服務。高校通過系統的創業教育,較為深入的掌握學員的各種情況,創業支持才能發揮更好的效果。 政府要加大對創業教育的扶持力度。首先,在國家的號召下,地方政府應協助高校打造和諧的商科院校本科畢業生創業環境,通過制定項目申報優先批復、稅收減免等扶持政策,鼓勵大學生畢業后,尤其是就業存在困難的情況下開展創業活動;其次,地方政府可通過撥付專項資金在高校成立創業基金,搭建政府、高校與投資公司三方投資平臺引入天使投資資金等形式解決創業啟動資金缺口,加快本科畢業生創業項目的孵化;此外,地方政府還應完善相應的法律法規保障商科院校本科畢業生創業期間所擁有的權利,明晰高校、商科院校本科畢業生、投資公司等各方的利益分配關系,并提高政府服務創業工作人員的能力與工作效率,為高校商科院校本科畢業生創業群體營造良好的政策環境,降低本科畢業生創業成本的投入,產生更大的創業熱情。
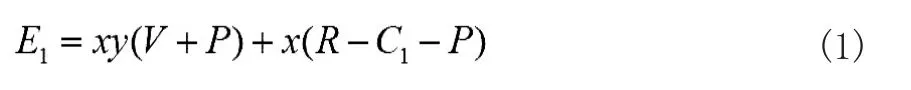



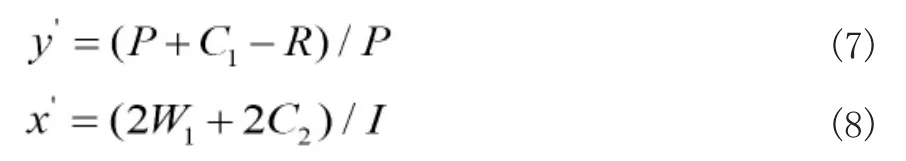
三、創業行為選擇過程中高校與商科院校本科畢業生之間的演化博弈分析
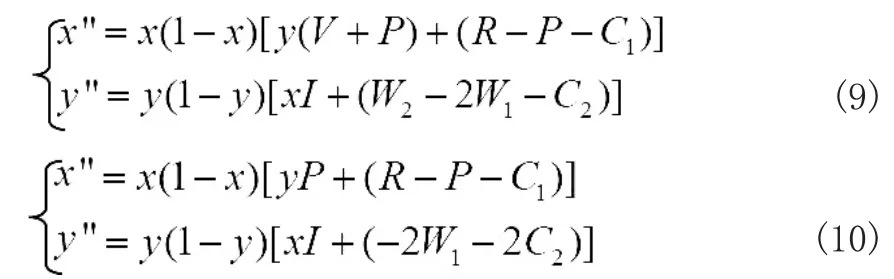
(一)基于高校的演化路徑分析,該情況下可從兩個方面進行討論
(二)基于商科院校本科畢業生的演化路徑分析,該情況下同樣可從兩個方面進行討論
四、結論及建議

