基于軌道檢測參數的高速列車車體振動預測方法*

卑王璐, 鐘倩文, 鄭樹彬, 羅文成， 彭樂樂

(1.上海工程技術大學 城市軌道交通學院, 上海 201620；2.常州路航軌道交通科技有限公司，江蘇 常州 213000)

0 引 言

中國軌道列車運行呈高速化與重載化發展趨勢，由軌道磨損、不平順等因素而引發的車輛振動愈發加劇[1]，強烈振動變化會影響列車運行舒適度。針對該問題，有必要對高速列車車體振動進行準確預測，但影響車體振動因素眾多且其相互耦合關系復雜，所以如何利用好既有的軌檢車檢測軌道數據，建立快速預測評估模型，準確預測車體振動情況，對高速列車的穩定運營具有重要的意義。

徐磊、陳雙喜、Li X等人建立傳統車輛—軌道動力學模型[2～6]并施加軌道不平順激勵求得車體振動響應預測，但以經驗軌道譜不平順作為激勵難以與現場實際應用達成一致。包學海等人依據多體動力學理論，郭訓等人根據有限元分析理論，分別建立了幾種車輛—無砟軌道—路基的耦合振動模型[7～9]，仿真出不同車速下或者軌道扣件不同工況下對車輛加速度的影響，但由于不同車輛建模參數各不相同，故只以車輛動力學建模預測振動，其精度難以保障。

機器學習的方法對列車振動分析具有高效率、高魯棒性的特點。Qian K等人建立了基于神經網絡和多體動力學模型的車輛振動加速度預測模型[10]。耿松建立了軌道不平順狀態下的神經網絡車輛振動預測模型[11]。Xie J 等人用深度信念網絡[12]對傅里葉變換處理后的振動信號進行特征提取訓練。徐碩建立了基于PCA-SVM方法的車體振動狀態分類預測模型[13]。而以上的機器學習預測方法都缺乏結合車輛動力學理論有效篩選振動相關檢測參數的前提，對車體振動的預測準確性有限。

針對上述研究分析，本文一種提出利用實際軌道參數進行CART回歸樹預測振動的方法。首先,使用Simpack仿真建立了車體振動和軌道幾何參數的聯系，然后,根據GJ—5軌檢車實測軌道幾何參數，使用CART回歸樹建立了車體振動預測模型。將預測值同實際振動值進行實驗驗證，并就模型評價指標與BP神經網絡、Interactions線性回歸和線性支持向量機(support vector machine,SVM)進行比較，證明了本文預測方法的準確有效性。

1 CART回歸樹預測模型

回歸樹算法使用局部數據對周圍復雜數據點進行建模從而簡化建模復雜度。其通過決策點的建立來分割預測的相關數據，并使用回歸算法對分割后的局部數據進行訓練，相較于其他回歸算法，回歸樹比較適合對復雜數據與非線性數據的建模[14]。

1.1 CART回歸樹生長

CART回歸樹構建原則是從根節點開始將樣本集的屬性與數特征節點比較，根據比較結果將樣本集劃分成不同的子節點。每個子節點再根據樣本子集的值范圍繼續進行比較，直到葉節點為最終決策結果。其針對連續數據的分裂準則是回歸方差[15]，選擇回歸方差最小的數據作為最優分裂點，最后預測結果就是所有葉節點的平均值。

將與車體振動相關的樣本數據集劃分為L個單元α1,α2,…,αL,且每個單元αl都有一個固定的輸出振動加速度值Cl。故回歸樹模型可表示為

(1)

模型輸出值與測量值之間的平均誤差為

(2)

根據分裂原則，平均誤差在Cl為所有實際車體振動值的平均值時達到了最優

Cl=ave(yi|xi∈αl)

(3)

1)最優切分變量和最優切分點的尋找

假設數據集第i個變量x(i)作為切分變量和其取值s為切分點，則該數據集可定義為2個區域

α1(i,s)={x|x(i)≤s},α2(i,j)={x|x(i)>s}

(4)

為尋找最優的i和s，定義c1,c2為區間的均值并求解如下

(5)

2)回歸樹歸納算法

將數據集經過式(4)～式(5)求解出最優解(i,s)，以此劃分區域并在各自子區間中確定區間的輸出值

α1(j,s)={x|x(j)≤s},α2(j,s)={x|x(j)>s}

(6)

(7)

根據上述步驟遞歸地對劃分出的2個子空間，繼續進行劃分，直至節點變為純性節點。最終，將輸入空間劃分為L個區域形成決策樹為

(8)

1.2 CART回歸樹剪枝

為防止CART決策樹的建樹過程中出現過擬合現象，利用使用k折交叉驗證法[16]，來測試回歸樹生長產生的子樣本分支是否需要修剪。首先，將數據集分為k組，以k-1組訓練集使樹生長，最后，用1組驗證集測試其分支規則是否重現并決定剪枝。重復k遍模型驗證遍歷，并最終平均k組預測值得到最終估計預測值。

1.3 模型評價指標

為更直觀地描述模型預測效果，采用擬合度(R-squared)、平均絕對誤差(mean absolute error,MAE)、均方根誤差(root mean square error,RMSE)等模型評價指標對預測算法進行評價。公式如下

(9)

(10)

(11)

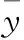
2 實驗數據獲取

2018年，GJ—5軌檢車在廣深Ⅱ線采集了37種參數，為篩選其中與車體振動強相關參數，本文使用SIMPACK建立車輛動力學模型，以軌道激勵的形式仿真車體振動同軌道不平順的關系，從中篩選出預測模型樣本數據集。

2.1 車輛動力學建模

本文通過SIMPACK建立了高速車輛動力學模型[17]，簡化車輛系統為車體、構架和輪對等為7個剛體，各構件自質心左右、前后對稱等。建模過程中將軌道狀態視為激勵源，以施加軌道譜激勵的形式，通過車輪向系統輸入。車輛模型重要參數如表1所示，車輛簡化動力學模型如圖1所示。

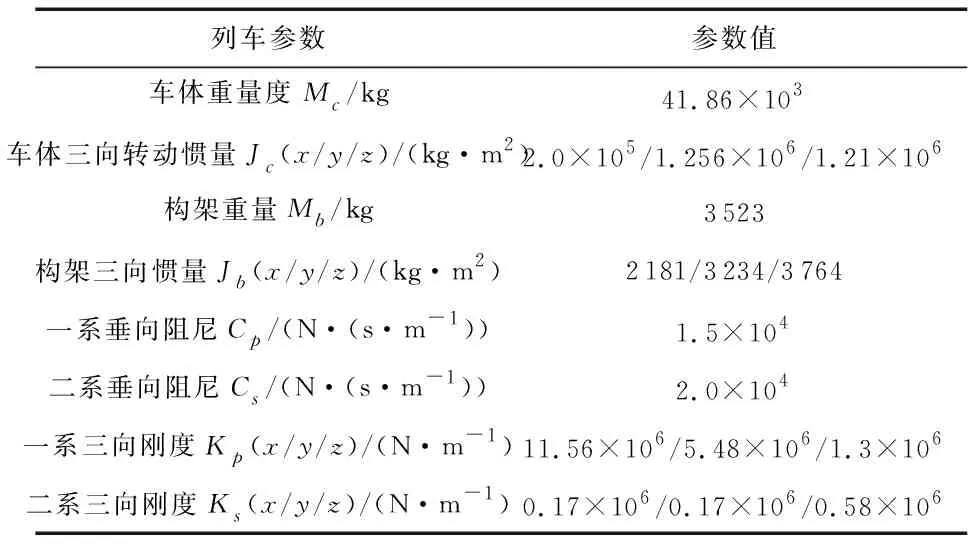
表1 車輛模型重要參數

圖1 車輛簡化動力學模型

2.2 車體振動仿真分析

由于中國尚未建立統一軌道功率譜標準，因此，為分析軌道不平順對車體振動的影響，選取常用的德國高速軌道譜[18]激勵輸入所建立的模型，分別更改其中的3種不平順譜為低速譜值，對比其輸出的車體振動變化如圖2～圖4所示。

圖2為橫向不平順譜值更改時的仿真車體振動特性圖。可知橫向不平順的變化，大幅度會影響車體橫向振動，其余2個方向振動幾乎無影響。

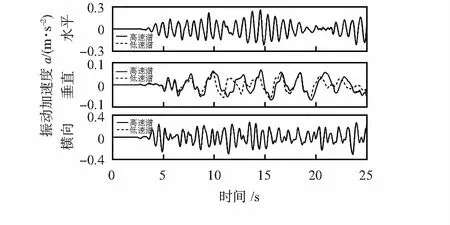
圖2 橫向不平順車體振動對比

圖3為垂向不平順譜值更改時的仿真車體振動特性圖。可知垂向不平順的變化，對車體水平和垂向振動有較多影響，對橫向振動幾乎沒有影響。

圖3 垂向不平順車體振動對比

圖4為水平及軌距不平順譜值更改時的仿真車體振動特性圖。可知水平及軌距不平順的變化，對三向車體振動均有一定且較大的影響。

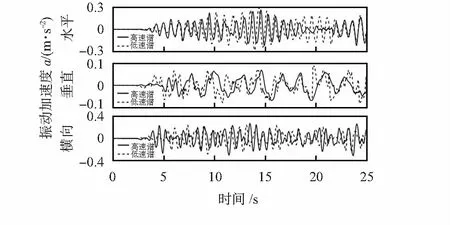
圖4 水平及軌距不平順車體振動對比

綜上所述可知，軌道不平順功率譜對車輛三向振動都有較大的影響。而軌道不平順實際就是由對線路實際測量尺寸的隨機波樣本，從空域、時域、幅值域等方面的描述。以此為依據，從既有軌檢車檢測參數中篩選軌道幾何檢測類共30種檢測參數，作為機器學習預測模型的樣本數據集，如圖5所示。

圖5 GJ—5軌檢車檢測內容

3 實驗與分析

視GJ—5軌檢車采集的軌道幾何檢測參數為訓練集，使用CART回歸樹算法并采用10折交叉驗證進行樹剪枝，設置該算法模型的最小葉節點樣本數為12，建立了CART回歸樹的車體振動預測模型。并以同樣的訓練集，分別訓練并建立BP神經網絡模型、Interactions線性回歸模型和線性SVM模型，同本文模型的評價指標進行對比如表2～表4所示。

表2 車體水平振動預測模型評價指標

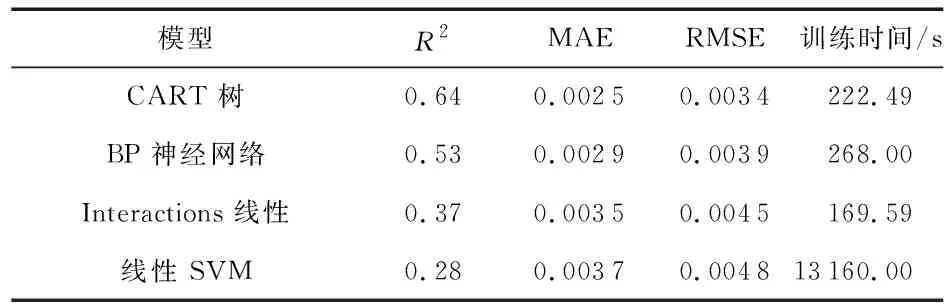
表3 車體垂直振動預測模型評價指標

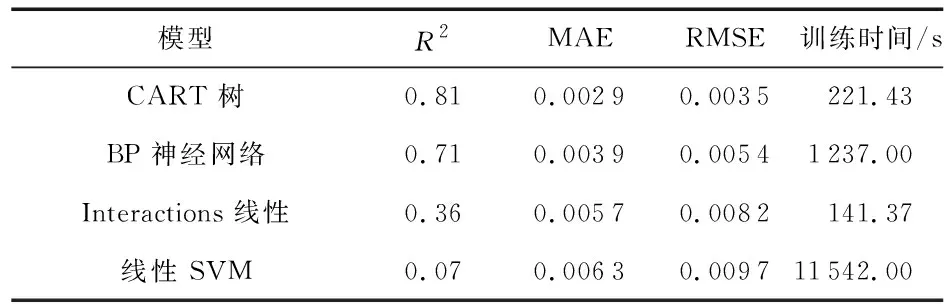
表4 車體橫向振動預測模型評價指標

由表2～表4可看出：在3個方向的車體振動預測中，CART回歸樹預測模型的擬合度都最高，誤差值都最低。該預測模型的擬合度水平方向可達0.88，MAE最小誤差達0.002 5，RMSE最小誤差達0.003 4，且模型預測時間較短。證明采用CART回歸樹算法在預測精度方面是一種較好的能夠反映車體振動情況的方法。

此外將CART回歸樹模型預測的車體三向振動加速度與該線路高速列車100 km/h狀況下實際振動加速度對比如圖6所示。從圖6中可直觀地看出：CART回歸樹預測的車體三向振動值整體變化趨勢與實際值保持一致，能夠較好地反映車體振動情況。僅在加速度振動趨勢突變處有一定偏差，其原因可能是由于樣本數據集缺乏超限情況而造成的，此數據取自軌檢車實測軌道幾何參數，因此,需在實驗室進一步補充各種超限工況進行改進與完善。

4 結 論

針對有效預測高速列車車體振動的問題，提出一種基于軌道幾何檢測參數的CART回歸樹車體振動預測方法。使用Simpack仿真建立了車體振動和軌道幾何參數的關系，然后篩選GJ—5軌檢車實測軌道幾何參數作為樣本數據，利用CART回歸樹算法，訓練數據集并構建了車體振動預測模型。同其他預測模型對比，CART回歸樹預測模型在精確度和訓練時間上有一定優勢，對車體振動預測及保證列車乘坐舒適度具有重要參考意義。下一步將考慮優化模型精確度并增加超限工況數據進行更為準確的預測。