基于改進猴群算法優化ADRC的PMSM矢量控制策略*

易靈芝， 王藝皓， 李 旺， 陳 章， 李進澤

(1.湘潭大學 自動化與電子信息學院,湖南 湘潭 411105；2.大功率交流傳動電力機車系統集成國家重點實驗室,湖南 株洲 412001； 3.中車株洲電機有限公司,湖南 株洲 412001)

0 引 言

永磁同步電機(permanent magnet synchronous motor，PMSM)廣泛應用于電動汽車、航空航天、智能機器人等行業[1]。相較于三相異步電動機，有更高的功率因數和硬機械特性[2,3]。為提高PMSM控制性能，文獻[4]利用CKMTOA-KELM最優回歸模型對擴展狀態觀測器中擾動量進行預測，有效提高了電機抗干擾能力;文獻[5]通過使用離散終端滑模控制律提高了永磁直線電機的位置跟蹤性能;文獻[6]設計了一種基于指數趨近律的滑模控制器，在PMSM啟動時能較快達到預定轉速;文獻[7]使用重復控制的PMSM矢量控制方案，通過周期性地補償誤差，改善電機控制性能。針對比例—積分(proportional integral,PI)控制調速系統很難滿足電機高精度控制問題[8]，學者韓京清保留了PI控制優點，提出了自抗擾控制(active disturbance rejection controll,ADRC)技術[9]。但由于跟蹤微分器與非線性狀態誤差反饋率中的Fal(e,α,δ)函數存在拐點,導致ADRC輸出信號抖動、抗擾動性較差。

綜上所述，本文提出了一種基于改進的猴群算法(im-proved monkey algorithm，IMA)優化改進ADRC的PMSM控制策略。該策略有效減少ADRC控制器[10]對參數設置的依賴；通過構造出新型非線性函數，顯著降低ADRC輸出補償時的信號抖動。

1 基于改進型ADRC的PMSM調速控制系統

1.1 ADRC原理

跟蹤微分器能準確地提取出給定信號中的微分信號，進而消除系統的初始誤差[11]。以二階系統為例，其離散形式[12]為

(1)

式中v(t)為電機的參考轉速，r為速度因子，h為采樣步長，v1(k)為函數v(t)在kh時刻的值，h0為跟蹤微分器的濾波因子。

擴展狀態觀測器能夠將電機所受到的總擾動以一種新的狀態變量的形式輸出，并且可以對此狀態變量進行實時觀測。其表達式如下所示

(2)

非線性誤差反饋律[13]表達式如下

(3)

式中 選擇合適的β參數可得到系統精確的控制量u0，實現控制目標。

1.2 ADRC的改進原理

為避免ADRC控制系統出現抖振現象，需Fal(e,α,δ)函數在原點以及分段點處盡可能平滑。當e>0時，對Fal(e,α,δ)函數求導，得到該函數在變量大于0時的微分形式為

(4)

在分段點δ處Fal′(e,α,δ)的取值為

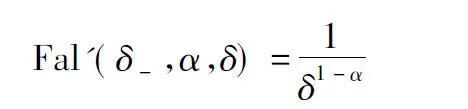
(5)

Fal′(δ+,α,δ)=αδα-1

(6)

當Fal(e,α,δ)在分段處可導時，存在Fal′(δ-,α,δ)=Fal′(δ+,α,δ)，此時α與δ需要滿足

=αδα-1

(7)

求解后可得α=1，當α=1時，Fal函數將變為線性的恒值函數，不滿足ADRC對最優控制函數非線性特性的需求。當α≠1時，將無法滿足式(7)的要求。為此，本文提出在原有函數的基礎上利用反正切函數、二次函數、三次函數以及差值擬合法構造出新型非線性Fal函數，構造思路如下：

新型控制函數在|e|>δ時表達式仍然為

nFal(e,α,δ)=sign(e)|e|α

(8)

當|e|≤δ時,新型控制函數的表達式為

nFal(e,α,δ)=a1·arctane+a2·e2+a3·e3

(9)

為保證函數在全部定義域內連續可導，需要滿足如下條件

(10)

將式(8)、式(9)代入式(10)，得到式(10)中的系數為

(11)

將式(11)中系數代入式(9)中，即可確定新構造的最優控制函數表達式。

1.3 基于改進型ADRC的PMSM調速控制系統原理

對PMSM數學模型進行推導

(12)

為得到系統控制量以及擾動量信息，對式(12)進行進一步等效變換

(13)

式中f(t)為系統不可觀測擾動。

基于改進ADRC控制器的PMSM控制調速系統如圖1所示。

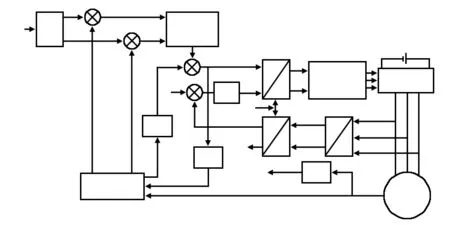
圖1 基于改進型ADRC控制器的PMSM調速系統框圖

2 IMA優化改進型ADRC的PMSM控制系統

2.1 猴群算法原理

猴群算法(monkey algorithm,MA)通過模擬猴群的“攀爬”、“觀跳”、“空翻”等動作抽象出算法尋優步驟[14,15]。

攀爬過程：MA通過“偽梯度”的操作來實現該步驟。猴群中第i只猴子的位置為攀爬步長為為隨機向量，向量中元素的產生規則為

(14)

式中R為介于0～1的隨機數。Xi所對應適應度函數的偽梯度函數值f′i(Xi)為

(15)

式中f′ij(Xi)為目標函數值。通過偽梯度函數值可得到候選解位置

(16)

觀跳過程：當觀跳視野長度為s2時，可基于舊解Xi與視野長度s2產生候選解，產生規則為

(17)

空翻過程：空翻過程決定MA算法的搜索范圍，空翻過程的候選解為

(18)

2.2 MA算法的改進

1)引入反向學習

為了擴大算法的搜索空間，引入反向學習策略。反向學習的表達式為

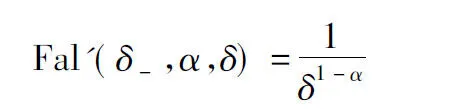
(19)

式中分別為猴群個體i在j維上的位置值和反向位置值；aj與bj分別為j維的下界與上界。

2)引入自適應權重系數

為了提高MA算法的全局尋優能力與局部尋優能力,參數的自適應計算公式如下

(20)

式中分別為s1與s2的最大值與最小值； (s4-s3)max,(s4-s3)min分別為(s4-s3)的最大值與最小值；Max_iter為最大迭代次數。

3)引入混沌正余雙弦搜索機制

Logistic映射公式為

Zk+1=μZk(1-Zk)

(21)

式中Zk為(0,1)空間的數值；μ為Logistic映射控制參數，取值范圍為[0,4]。當候選解取值范圍為[lb,ub]時，實數域空間與(0,1)空間的轉換關系為

X=lb+(ub-lb)Z

(22)

式中Z為Logistic映射后得到的數值；X為在[lb,ub]范圍內Z所對應的實數值。

以候選解作為初始最優值，采用正余雙弦算法進行搜尋，搜尋公式為

(23)

式中S為得到的新解；S*為搜尋過程中得到的最優值；r1取值如式(24)所示

(24)

式中τ為正常數；h為當前搜尋次數；H為預設的總的搜尋次數。Metropolis接受準則計算公式為

(25)

3 仿真與實驗分析

3.1 仿真結果分析

為證明所提方法的有效性，使用MATLAB搭建了IMA算法優化改進型ADRC的PMSM仿真模型。PMSM參數如表1所示。

表1 永磁同步電機參數設置

1)高速工況下突加負載:給定PMSM轉速為1 000 r/min，運行至0.2 s時突加10 N·m負載轉矩。仿真結果如圖2、圖3所示。

圖2 突加負載時的轉速波形

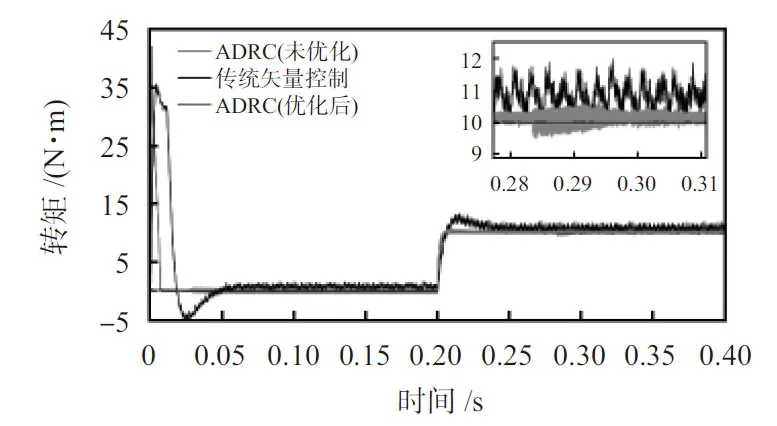
圖3 突加負載時的轉矩波形

2)高速情況下改變參考轉速:給定PMSM初始轉速為1 000 r/min，運行至0.2 s時將參考轉速設置為-1 000 r/min。仿真結果如圖4、圖5所示。

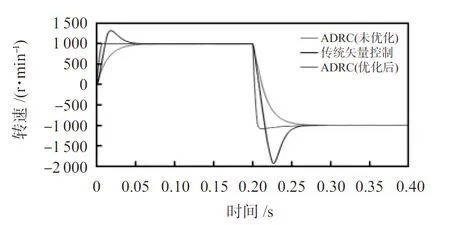
圖4 改變參考轉速時的轉速波形

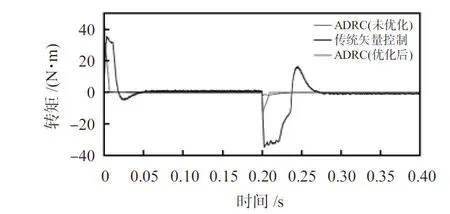
圖5 改變參考轉速時的轉矩波形

3)低速工況下突加轉矩:仿真設置為給定PMSM轉速為100 r/min，運行至0.2 s時突加負載轉矩10 N·m，仿真結果如圖6所示。

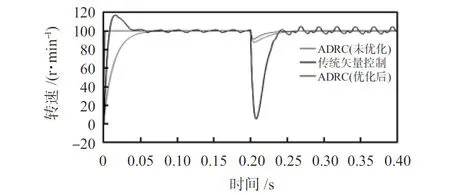
圖6 突加負載時的轉速波形

3.2 實驗結果分析

本文以TMS320F28035DSP芯片為基礎，搭建了PMSM控制系統實驗平臺。該實驗平臺主要由控制電路板、兩臺參數一致的電機、示波器、電腦、斷路器組成。且安裝有扭矩傳感器、速度傳感器。本文所提出的控制算法和軟件程序在CCS軟件中編程實現，并通過仿真器下載到F28335DSP芯片中。在空載的情況下啟動進行實驗。

分析圖7，當負載發生突變時，基于IMA優化改進型ADRC控制器的PMSM轉速恢復至參考值的時間相較于傳統ADRC來說更短，且能夠有效降低電機在轉矩突變時所帶來的轉矩脈動。

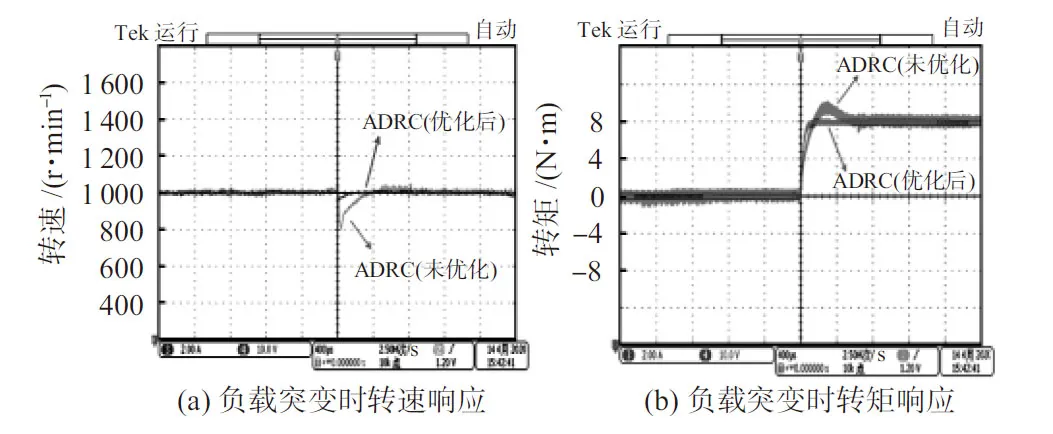
圖7 負載突變時轉速與轉矩的響應測試

4 結 論

為了提高PMSM控制系統的魯棒性和動態響應速度，本文提出了一種利用差值擬合法對ADRC的控制函數進行重構，得到了一種新型的ADRC控制器的方法，并將其應用于PMSM的性能調節。此外，考慮到ADRC控制器待整定參數較多，本文采用MA算法對其進行整定，并針對傳統MA算法的不足，提出系列改進策略。最后通過實驗結果分析可知，本文所提ADRC控制器改進策略可明顯提高PMSM控制系統的控制精度與魯棒性。