三方眾包市場中的發包方平臺博弈機制設計
何雨橙 丁堯相 周志華
(計算機軟件新技術國家重點實驗室(南京大學) 南京 210023)
隨著機器學習任務的規模逐漸增大,人們迫切需要對大規模數據進行收集.眾包(crowdsourcing)作為低成本高效率的數據收集方式,受到了廣泛歡迎.
眾包研究的基本問題之一是設計有效的機制以使得參與者在競爭中實現共贏.當前,眾包機制設計研究往往基于兩方眾包模型:發包方(requester)發布任務并支付標注者(workers)費用;標注者完成任務并收取報酬[1].該模型的重要假設在于發包方和標注者可以直接進行交互.而現實應用中,如圖1所示,發包方和標注者的交互往往以平臺(platform)為中介,構成三方眾包市場.其中,發包方將任務和報酬發布給平臺,平臺雇傭標注者進行標記,進而在將標記結果反饋給發包方的同時,賺取支付給標注者的費用和發包方支付給自己的費用之間的差價.顯然,傳統的兩方眾包模型無法對該過程進行建模,因此需要引入全新的三方眾包模型進行研究.
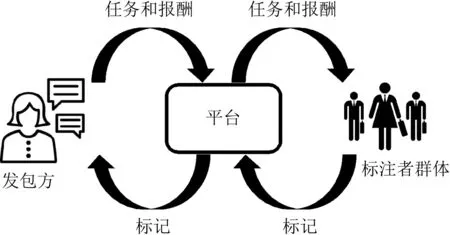
Fig. 1 The three-party crowdsourcing market圖1 三方眾包市場示意圖
相比于兩方眾包,三方眾包的核心問題是發包方與平臺之間的博弈:發包方希望支付較少的報酬同時獲取準確率較高的標記;而平臺則希望降低雇傭標注者的成本,同時從發包方處獲取較多的報酬.這之中存在著復雜的博弈關系.一方面,發包方和平臺既有合作也有競爭:雙方都希望最大化標記的準確率,但在最小化或最大化發包方支付這一點上有沖突.另一方面,發包方和平臺各自只能掌握自身信息,而無法直接觀測到對方信息.在不完全信息下采取最優策略,對雙方都是相當具有挑戰性的問題.
本文開啟三方眾包市場中的發包方-平臺博弈機制設計研究,主要貢獻有4點:
1) 提出不完全信息博弈[2]模型CrowdMarket對三方眾包市場進行建模,并證明通過設計合適的在線學習策略可以近似達到該博弈的Nash均衡;
2) 在單發包方設定下,證明了EXP3算法[3]為發包方的最優策略,進而本文設計了基于反事實遺憾最小化(counterfactual regret minimization, CFR)技術[4-5]的平臺策略,證明該策略能夠充分利用平臺方的有效信息,具有比直接應用傳統在線學習方法更強的理論保證;
3) 將單發包方的策略拓展到多發包方的情形,并給出了多發包方情形下的理論分析;
4) 通過合成及真實數據集上的實驗驗證了方法的有效性.
1 相關工作
眾包研究的核心問題之一在于如何平衡標記質量和支付費用[6-7].現有研究中,實現這一目標的方式可以分成2類:設計更好的標記推斷方法以及設計更好的眾包機制.標記推斷已經有了豐富的研究,例如文獻[8-11].本文則著力于探討機制設計問題.
兩方眾包機制設計已經得到了充分研究,其中包括任務與報酬的分配機制設計[12-15],以及利用提供線索[16]或跳過選項[17-19]等方式提升高難度樣本的標記質量.由于這些機制都是針對標注者的,因此這些策略同樣可以應用于三方眾包市場中作為平臺與標注者之間的博弈機制.并且由于這方面的研究相對成熟,本文不再對此進行深入探討.同時,也有大量的研究關注如何設計合適的支付策略以激勵標注者給出高質量的標記.這方面的代表性工作包括文獻[20-23].在我們的問題設定中,這些激勵機制可以被平臺用于激勵標注者給出更準確的標記,但是不能直接用于處理平臺和發包方之間的博弈.
近期以來,一些工作也開始從應用的角度關注三方眾包市場.例如文獻[24]提出了一種聲譽評價方法以防止發包方和標注者的欺騙行為,而文獻[25]則將眾包市場建模為一個3層的優化問題以最大化平臺的健康度.但這些工作均不涉及博弈機制設計研究,因而它們的研究動機與本文有著顯著的差異.
當前,將眾包形式化為博弈問題,特別是預算有限條件下的收益最大化問題,是一個重要的理論研究方向[26-28].這個方向上的現有研究主要集中于傳統兩方設定,本文所提出的三方眾包模型,對拓展這一方向的研究內容可能起到有益的作用.此外,近期也有工作研究如何在廣告市場中利用機器學習方法從數據中學習有效的三方博弈機制[29].本文的研究也為將這種新方法引入眾包博弈問題提供了有益啟示.
2 CrowdMarket模型
2.1 基本定義
本節提出三方眾包模型CrowdMarket,將三方眾包市場形式化為發包方、平臺以及標注者三方的不完全信息博弈[2].本節討論單發包方情形,第4節中將對多發包方情形進行討論.
單發包方情形下的CrowdMarket模型為持續T輪的博弈,在第t輪下:
1) 發包方發送一個包含b個任務的任務包,以及支付報酬xt∈(0,1]給平臺.本文假設發包方只能從有限數量的K個報酬選項X1,X2,…,XK中選擇合適的報酬.
2) 在收到報酬和任務包之后,平臺選擇mt個標注者完成標注任務.
3) 標注者各自選擇采取低等級的努力或者高等級的努力以完成任務.高努力下準確率為p*>1/2;而低努力下標注者隨機猜測以返回標記,準確率為1/2.之后每位標注者各自獨立地為每個任務進行標注,并將結果反饋給平臺.
4) 平臺將每位標注者給出的標記通過多數投票法進行集成,并將集成后標記返回給發包方.集成后標記的實際平均準確率記為at.發包方從返回的標記中得到的收益取決于該準確率以及支付給平臺的報酬,因此可以表示為at-xt.
5) 平臺從發包方的支付中取出一部分作為參與了本輪標注的標注者的報酬,其余作為自己的收益.
為了激勵標注者給出高質量的標記,平臺需要得知標注者給出的標記的準確程度,這就需要發包方向平臺提供反饋.因此,我們引入了這樣一個步驟:發包方在每一輪結束之后會向平臺反饋該輪標記的準確率.參考文獻[17],可以設計激勵機制來確保發包方會誠實地反饋標記準確率,在3.1節中我們將會給出該激勵機制并進行分析.另外,本文假設平臺只能有部分輪次得到真實標記.因此,平臺不能在任意輪次中直接推斷出標記準確率.
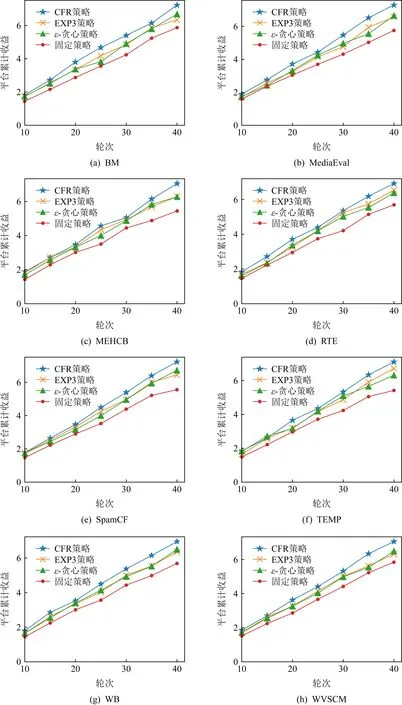
每一輪中參與者可能選擇的動作組成的集合稱為動作集.具體而言,發包方的動作集為Areq={(x,a′):x∈{X1,X2,…,XK},a′∈[0,1]},其中x代表支付給平臺的報酬,a′代表匯報的準確率;平臺的動作集為Apla=(m,c):m∈{1,2,…,N},c∈N},其中m代表平臺選擇標注的人數,c代表為每一位標注者支付的報酬組成的向量(m CrowdMarket模型是一個多方非零和博弈[30],這是博弈論中最難分析的博弈類型.但是,該模型有特殊的結構:發包方和標注者之間并沒有直接的交互.利用這一點,我們可以將CrowdMarket模型分解成2個部分:發包方和平臺之間的博弈以及平臺和標注者之間的博弈.其中,平臺和標注者之間的博弈與傳統的兩方眾包中發包方和標注者之間的博弈是類似的,因此平臺需要設計機制以激勵標注者采取高等級的努力.并且,需要同時引入激勵機制使發包方誠實反饋準確率. 本節介紹平臺需要采用2個激勵機制:1)激勵發包方誠實反饋準確率信息的機制;2)激勵標注者采取高等級努力的機制. 在CrowdMarket模型中,平臺可以獲得發包方反饋的準確率信息a′t.但是,發包方可能會試圖通過反饋一個虛假的準確率a′t進行欺詐.為了防止這一點,受到文獻[17]中“沒有免費的午餐”(no-free-lunch)原則的啟發,我們為平臺設計了一個懲罰機制以防止發包方欺詐. 本文假設在CrowdMarket博弈過程中,平臺可以隨機選取某些輪次通過第三方得到真實標記,進而在這些輪次中對發包方反饋的標記準確率進行驗證.如果驗證發現發包方反饋的準確率不正確,即發包方在該輪進行了欺詐,那么平臺將會對發包方進行一定的懲罰. 我們首先定義指示變量序列yt,t=1,2,…,T如下: 懲罰機制可以表示為指示變量序列的一個函數f(y1,y2,…,yT):在眾包博弈結束后,發包方需要支付f(y1,y2,…,yT)給平臺作為欺詐的懲罰.為了確保公平性,懲罰機制需要滿足2個基本條件: 第1個條件是平臺不能在沒有發現發包方欺詐的情形下進行懲罰;相反,如果發包方被發現在每輪都作弊了,那么需要支付最大數額的懲罰金額Fmax.該條件可以形式化為定義1. 定義1.如果懲罰機制f滿足: 1) 若yt≠1對所有t=1,2,…,T成立且存在t使得yt=-1,則f(y1,y2,…,yT)=Fmax. 2) 若yt=1對所有t=1,2,…,T成立,則f(y1,y2,…,yT)=0. 則稱f滿足“沒有免費的午餐”條件. 第2個條件是發包方應該支付懲罰當且僅當其被發現有欺詐行為.該條件可形式化為定義2. 定義2.如果懲罰機制f滿足:對于任意輪次t∈{1,2,…,T}以及任意 (y1,…,yt-1,yt+1,…,yT)∈{-1,0,1}T-1 都有 f(y1,…,yt-1,1,yt+1,…,yT)= 那么稱f滿足“激勵相容”條件. 基于這2個條件,我們提出如下機制: (1) 其中,I(yt≠-1)為指示函數. 式(1)表明:如果被發現在眾包過程中有欺詐行為,發包方會支付最大數額的懲罰.顯然,式(1)所述的機制滿足我們提出的2個條件.我們可以進一步證明定理1成立,定理1表明了由式(1)定義的懲罰機制是滿足我們所要求的2個條件的唯一機制. 定理1.當Fmax≥T2時,式(1)機制是唯一滿足“沒有免費的午餐”條件和“激勵相容”條件的機制,且發包方最優策略是每輪誠實反饋收益信息. 證明.假設f是同時滿足定理要求的2個條件的機制.我們只需要證明:當所有的指示變量yi≠-1時f(y1,y2,…,yT)=0,否則f(y1,y2,…,yT)=T即可. 1) 當?i∈[t]:yi≠-1時,我們假設y1,y2,…,yT中有k個1和T-k個0.不失一般性地,可以假設前k個變量取值為1,其余變量取值為0.由“沒有免費的午餐”可知: 2) 平臺僅在第t輪進行了1次檢查,且yt=-1.根據“沒有免費的午餐”條件,該情況下懲罰為Fmax.又由“激勵相容”條件易知,任何存在yi≠-1,i=1,2,…,T的情況下,懲罰均不應小于該情況,也為Fmax. 綜上即是該機制為唯一滿足條件的機制. 接下來考慮該機制下發包方作弊能得到的額外收益.考慮極端情況:發包方只需要在其中1輪作弊,未被發現即可得到最大收益R,被發現則要另外支付懲罰T.再設發包方不作弊得到的收益為r,平臺檢查的輪數所占比例為p.由于平臺至少檢查1次,因此p≥1/T.對發包方而言,不作弊是最優策略當且僅當 p(R-Fmax)+(1-p)R≤r, 解不等式得p≥(R-r)/Fmax.由于在CrowdMarket模型中,R-r≤T,因而上述不等式恒成立.這表明誠實反饋是發包方的最優策略. 證畢. 標注者i獲得的總收益為 (2) 式(2)采用了一個簡單的機制:如果被發現在標注過程中有采取低等級努力行為,標注者將無法得到該輪報酬,否則等價于每一次標注都得到報酬ci.由于標注者的目標是最大化其收益,因而有定理2: 定理2.在式(2)機制下,標注者的最佳策略為在所有輪次均采取高等級努力進行標注. 證明. 由于標注者的目標為最大化其收益,在任意t≤T輪中,顯然只有當標注者采取高等級努力時,所收獲的單輪回報最大,進而知定理結論成立. 證畢. 注意到,由于標注者所標記的樣本是有限的,因而通過標注是否正確判斷其努力程度存在一定錯誤的可能性.在實際問題中,不難通過允許用戶對自身努力程度被錯判的情況進行申訴,來消除該錯誤. 在本節給出的激勵機制的保證之下,平臺可以保證在每一輪中:1)發包方誠實匯報準確率;2)標注者選擇高等級努力,因而給出的標記的準確率為p*;3)平臺向每位被分配任務的標注者支付報酬ci,由于標注者之間相互等價(能力與標注策略均相同),每位標注者的報酬均相同.在上述標注者策略已經固定的情況下,后文將集中研究如何設計發包方和平臺之間的博弈策略.另一方面,不妨將發包方與平臺已經確定的動作從動作集中移除,以重點研究還未確定的動作:發包方-平臺博弈的每一輪中,發包方的動作是選擇支付給平臺的報酬,平臺的動作是選擇分配的標注者人數.為此,在下文中我們重新定義發包方和平臺的動作集分別為Areq={X1,X2,…,XK},Apla={1,2,…,N}.發包方和平臺的策略空間也相應地重新定義. 本節介紹發包方和平臺在CrowdMarket博弈中采取的博弈策略.在4.1節我們證明發包方和平臺可以使用在線學習算法最小化自身遺憾;4.2節和4.3節分別給出發包方和平臺基于在線學習算法的策略. 每個參與者的目標均為最大化自身的累計收益,這等價于最小化自身的“遺憾”: 證明.首先以平臺為例進行證明.由ε-最優性的定義有 進而,由于平臺收益是線性函數,我們可以得出: 發包方的效用函數可類似地表示為策略的線性函數,從而同理可證 證畢. 由于Nash均衡狀態代表了各方策略同時達到穩定狀態,因而定理1表明,博弈各方只需采用能夠對遺憾進行最小化的學習策略,就能在競爭中合作共贏. 注意到發包方可以將博弈過程建模為賭博機(bandit)在線學習問題:發包方可能選擇的支付動作Areq可視為賭博機搖臂,博弈產生的收益可以作為選擇特定搖臂之后得到的收益.進而,發包方可以采用文獻[3]提出的EXP3算法作為其策略.下面的定理給出了任何發包方策略的遺憾下界,進而驗證了EXP3策略的最優性. 證明.考慮這樣一種情況,標注者能力p=1,即標注者總是返回真實標記;平臺通過以一定概率隨機反轉集成后標記的方式控制返回給發包方的標記準確率.假設當發包方選擇支付給平臺的報酬為x時,平臺翻轉標記的概率為1-q(x),即平臺提供的標記的期望準確率為a=q(x). 考慮函數q(x)=x+α+εI(x=x0),I()表示指示函數,并且α足夠小從而使得q(x)∈[0,1].顯然此時發包方的期望收益u=q(x)-x=α+εI(x=x0)滿足以上條件. 證畢. 這與EXP3的遺憾上界同階,因而EXP3是發包方在缺乏信息的條件下所能采用的最優策略.值得注意的是,平臺也可以由定理4得知發包方會使用EXP3策略.在4.3節我們會展示這一優勢是如何幫助平臺制定策略的. 此時信息很不充足,對標注者能力的估計誤差會很大.解決該挑戰的思路是,在每輪博弈中基于文獻[4]提出的CFR技術模擬之后的博弈過程.基于CFR的平臺博弈策略(以下簡稱CFR策略)如算法1所示: 算法1.CFR策略. ① 初始化置信區間I1=[0,1],P1={p:p∈I1}; ② 初始化歷史記錄H=?; ③ fort=1,2,…,T ⑥ 完成眾包并接收發包方反饋的收益at; ⑦ 將(mt,at)添加到H之中; ⑩ 更新It+1為 則有 (3) 其中,N為平臺最多可選擇的標注者人數. 另一方面,直接應用原始的CFR算法無法達到理想效果.這是由于對于平臺而言,標注者能力在博弈開始是未知的,必須通過對標注者能力進行有效估計,才能加快CFR算法的收斂速度.為了能更精確地得到對標注者能力的估計,算法1中引入了標注者能力估計步驟,利用Hoeffding不等式逐漸縮小標注者能力的可能取值范圍(算法1行⑤~,行⑩中b為每輪任務數,δ為置信系數).隨著博弈輪數的增加,參數區間會越來越緊,從而起到逐漸縮小標注者能力的可能取值集合的效果(算法1行).下述定理表明應用該策略可以達到更緊的遺憾界. 定理5.當博弈總輪數T充分大時,以至少1-δ的概率,算法1中的策略的期望遺憾上界為O(logT). (4) (5) 其中,εt表示模擬過程和真實過程之間有差異的平均概率.結合式(4)和式(5)可知,總的遺憾上界為 當t 證畢. 定理5說明算法1的遺憾界顯著優于EXP3策略,表明該策略充分利用了前文所述的額外信息. 本節討論多發包方CrowdMarket模型的博弈機制.如果標注者群體可以同時為所有的發包方提供服務,那么平臺只需要和每一個發包方單獨進行CrowdMarket博弈,此時多發包方和單發包方的情形是完全一致的.但是如果標注者群體在同一時間只能為部分發包方提供服務,那么發包方之間需要競爭服務的使用權.因此,本節針對后一種情況進行研究. 不失一般性,假設一共有n個發包方參與博弈,平臺在每一輪中為出價最高的發包方提供服務.同時,假設單個發包方只能知道自己是否成功獲得服務,而無法得知其他發包方的出價以及任務完成準確率信息.易知,在任何一輪當中,出價最高而得到服務的發包方的收益和單發包方的情形相同,而未得到服務的發包方的收益則為0. 與單發包方條件下類似,在多發包方條件下,發包方仍然面臨著缺乏決策信息的問題:不僅無法得知平臺如何雇傭工人,而且無法得知其他發包方的情況.因而,可以類似地證明發包方的最優策略為使用EXP3算法.接下來我們證明:平臺也仍可以使用CFR策略模擬多發包方的情形,以優化自身的遺憾. 定理6.在有n個發包方情形下,當博弈總輪數T充分大時,以至少1-δ的概率,CFR策略的期望遺憾上界為O(n(logn+logT)). 當T≥nT1時,至少有一個發包方在至少T1輪贏得服務,而對于贏得服務小于T1輪的發包方,與其博弈的遺憾界是常數階.進而知以至少1-δ的概率有 證畢. 本節對發包方-平臺策略性能進行驗證.具體而言,本節實驗對3點進行驗證:1)對于發包方,當平臺使用強對抗性的策略時,EXP3策略是否有好的表現;2)對于平臺,CFR策略是否能利用額外信息給出更好的結果;3)對于多發包方的情形,發包方EXP3策略及平臺CFR策略是否依然適用.實驗中發包方和平臺的動作集設定為:1)發包方可能的支付選項為{0.1,0.2,0.3};2)平臺可能選擇的標注者人數為{1,3,5};3)平臺雇傭每個標注者的成本C=0.01. 本節實驗使用8個二分類真實數據集:1)BM數據集[33],該數據集中標注者對語料給出正面或負面情緒標記;2)TEMP數據集[34],該數據集中標注者對2件事是否是先后發生的進行標記;3)WVSCM數據集[8],該數據集中標注者對圖片中人臉是否微笑進行標記;4)WB數據集[35],該數據集中標注者對圖片中的水鳥是否是鴨子進行標記;5)SpamCF數據集[36],該數據集中標注者對一個AMT平臺上的任務是否是垃圾任務進行標注;6)MediaEval數據集[36],該數據集中標注者對給定圖片是否和時尚有關進行標注;7)MEHCB數據集[37-38],該數據集中標注者對搜索請求和網頁是否有關進行標記;8)RTE數據集[34],該數據集中標注者對文本之間是否有蘊含關系進行標注.實驗所用8個數據集的相關信息如表1所示. Fig. 2 The cumulative rewards of requester strategies under the single requester setting圖2 單發包方情形下發包方策略的累計收益對比 本節在單發包方情形下,將發包方EXP3策略與ε-貪心策略(ε=0.05)及固定策略(始終固定在最高支付)進行性能對比.同時,假設平臺使用高對抗性甚至是作弊性質的策略,因為我們需要驗證即便在最壞情形下EXP3策略仍然有效. Table 1 Information About Datasets表1 實驗所用數據集的相關信息 在我們的實驗中,平臺和發包方用各自的策略進行持續T輪的CrowdMarket博弈.輪次上限T的取值分別設定為10,15,…,40.本實驗中假設平臺可獲取真實的標注者能力p*,從而可以通過以一定概率翻轉標記的方式準確控制返回給發包方的標記準確率.并且,平臺會采用如下強對抗性的策略以誘導發包方提高支付:平臺以一定的概率q翻轉標記,之后如果平臺收到了更高的報酬則會逐漸降低q的取值.平臺采用的這一策略要求發包方逐漸提高支付的報酬而不能只用貪心策略.本次實驗中設定初始輪次中q=0.50,每次收到更高報酬后q的降低量分別設為0.02,0.03,0.04,0.05.在每組參數下我們重復實驗50次并匯報平均累計收益.實驗結果如圖2所示,實驗結果可見,當平臺使用強對抗性的策略時,發包方使用EXP3策略獲得的累計收益總是比ε-貪心策略和固定策略要好,這表明了EXP3策略的有效性. 本節驗證了3個發包方情形下,發包方使用EXP3策略的有效性.博弈過程的參數設定同6.1節. 為了驗證EXP3策略的有效性,在實驗中我們令3個發包方分別使用EXP3策略、ε-貪心(ε=0.05)策略和固定策略,平臺使用的策略為CFR策略.我們令3個發包方在CrowdMarket博弈中使用不同策略相互競爭,勝出的發包方所使用的策略就是這3個策略中最優的策略.為了保證公平性,所有發包方使用的數據集都是一樣的,以確保標注者能力對于所有發包方是一致的.我們在8個數據集上進行了實驗,每個數據集上重復10次.發包方累計收益的平均值如圖3所示.可以發現,使用EXP3策略在絕大多數時間內都能獲得最多的收益,這表明EXP3策略在多發包方的情形下依然適用. Fig. 3 The cumulative rewards of requester strategies under the multiple requester setting圖3 多發包方情形下各發包方策略的累計收益對比 為了驗證平臺在單發包方與多發包方情形下使用CFR策略的性能,我們將CFR策略和EXP3策略、ε-貪心(ε=0.05)策略以及固定策略進行了對比,發包方的策略固定為EXP3策略.博弈過程的參數設置與6.1節相同.單發包方情形下我們在8個數據集上進行了實驗,在多發包方情形下則測試了2組發包方數據集的組合,所有實驗結果如圖4所示.每張子圖展示了平臺的累計收益.實驗結果顯示:無論在哪個數據集上,性能最好的策略均為CFR策略,其次是EXP3策略,再次是ε-貪心策略,排名最后的是固定策略.這表明利用到了額外信息的CFR策略確實能取得更好的效果. Fig. 4 The cumulative rewards of the platform strategies under the single requester and multiple requester settings圖4 單發包方與多發包方情形下的平臺策略累計收益對比 表2展示了單發包方情形下,當平臺使用不同策略,發包方使用EXP3策略時,40輪之后平臺和發包方的合計累計收益.結果表明平臺使用CFR策略可以使得雙方的累計收益達到最大.綜合上述結果可知,CFR策略是最適合于合作的策略.注意到平臺使用CFR策略是在發包方反饋準確率信息時的最優策略,而平臺使用EXP3策略是在發包方不反饋準確率信息時的最優策略.因此,表2中平臺使用CFR策略時,累計收益超過EXP3策略,這表明2.1節中引入的反饋步驟可以提升雙方的累計收益,對于雙方的合作有促進作用. Table 2 Total Rewards of Platform and Requester After 40 Round with Different Strategies of Platform 在本節中,我們利用仿真數據集和真實數據集進行了實驗,對本文提出的基于在線學習方法的三方眾包市場發包方-平臺博弈策略進行了驗證.實驗結果表明,在符合CrowdMarket模型假設的條件下,本文提出的單發包方及多發包方策略不僅能優化自身的累計收益,而且能達到促進博弈雙方合作共贏的目的.這驗證了本文提出策略的有效性.另一方面,在實際應用中,也可能存在數據不符合CrowdMarket模型假設的情況.由于相關數據集的缺乏,難以驗證在這一條件下本文方法的實際效果.我們會在未來研究中探索這一問題. 本文針對三方眾包市場中的發包方-市場機制設計問題進行理論研究,提出三方眾包市場模型CrowdMarket.在該模型的基礎上,針對單發包方和多發包方的設定,研究平臺和發包方的策略設計和理論分析.真實數據集上進行的實驗驗證了本文所提出的策略的有效性.我們相信本文的研究結果可以激發更多針對三方眾包市場的研究,有助于更好地理解現實應用中眾包產業的市場行為. 作者貢獻聲明:何雨橙調研整理文獻,實施方法研究,完成實驗,撰寫論文;丁堯相設計研究方案,實施方法研究,修訂論文;周志華提出研究選題,指導方法研究與論文撰寫支持.2.2 CrowdMarket博弈的分解
3 平臺激勵機制設計
3.1 激勵發包方誠實反饋的機制
f(y1,…,yt-1,0,yt+1,…,yT)≤
f(y1,…,yt-1,-1,yt+1,…,yT),
3.2 激勵標注者采取高等級努力的機制
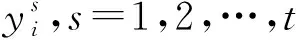
4 發包方-平臺博弈策略設計
4.1 基于在線學習的博弈策略
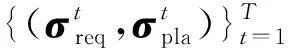

4.2 發包方策略



4.3 平臺策略



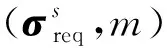

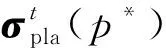


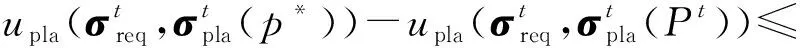




5 多發包方情形下的策略

6 實驗驗證

6.1 單發包方策略驗證

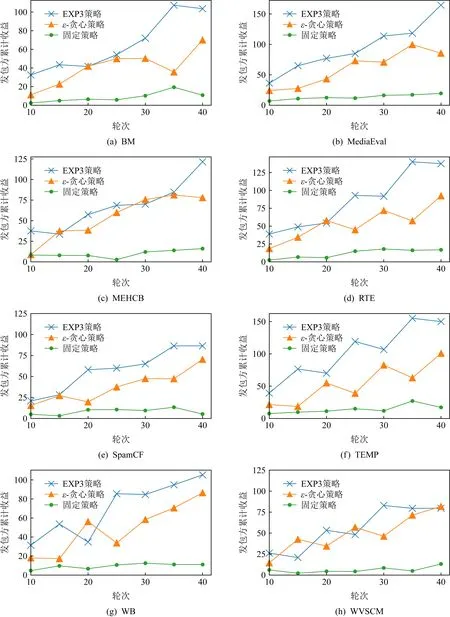
6.2 多發包方策略驗證
6.3 平臺策略驗證

6.4 實驗結果分析
7 結束語

