一種可選的電離層TEC 區域重構方法

車磊 歐明 陳奇東 蔡紅濤 甄衛民 陳龍江 靳睿敏

（1.中國電波傳播研究所,青島 266107；2.西安電子科技大學，西安 710071；3.武漢大學電子信息學院，武漢 430072）

引言

作為表征電離層變化的一個重要特征參量，電離層總電子含量(total electron content,TEC)反映了眾多電離層不同空間的變化特性[1-2].通過空間插值(spatial interpolation)的方法得到整個區域TEC 的預測值是TEC 區域重構常用的技術方法[3].由于電離層暴、太陽活動等自然現象的頻發，電離層TEC 的非線性、非平穩變化可能存在波動和異常，影響無線電波的傳播特性，不可避免地引起包括衛星導航、通訊、雷達和定位異常等問題[4]，因此，如何清晰地描述電離層TEC 的空間分布特征，準確地實現特定區域的電離層TEC 區域重構，完成電離層監測與預警，一直是相關領域研究的熱點和難點問題[4-5].

當前，對于區域電離層TEC 區域重構主要通過空間插值的方法來估算一定區域范圍內電離層TEC.這里提及的空間插值方法主要是基于已知觀測站點獲取的電離層TEC 真實值，通過插值的原理來估計其他位置站點的電離層TEC 預測值，其根本原理是通過基于構建的函數關系理論模型，綜合已知監測站點的電離層TEC 空間位置關系以及空間相關性，從而估算其他任意點的電離層TEC[6].空間插值方法本質上追求構建盡可能符合原始觀測數據的函數關系理論模型[7].

空間插值方法種類眾多，應用也十分廣泛.常用的插值方法包括反距離加權法、線性內插法、泰森多邊形法、樣條函數法、移動擬合法、趨勢分析法、克里金插值法等.克里金空間插值方法(Kriging interpolation)適用于樣本數據存在隨機性和結構性特征的場景，應用于空氣污染、降雨、環境監測等領域，并結合電離層TEC 空間分布的特殊性及相關性，得到了廣泛應用[8].克里金空間插值方法又稱空間自協方差最佳插值法[9]，基于區域化變量(regionalized variable)自身具有的隨機性特征和結構性特征為基礎，同時通過變異函數(variogram)對區域化變量進行空間描述，模擬地理現象空間分布的相關性和變異性，因此能夠挖掘區域化變量的空間結構和空間變化規律[10].電離層TEC 正是具有這種隨機性(不確定性)與結構性(相關性)雙重特征的區域化變量，應用克里金空間插值實現對電離層TEC 區域重構，其實質在于通過已經位置點的電離層TEC 內插或外推的方式，對待估位置點電離層TEC 的取值進行無偏、最優估計[11].

諸多專家學者通過克里金空間插值方法實現了電離層TEC 區域重構.Stanislawska 等人改進了克里金空間插值方法，通過加入電離層空間距離的影響因素，實現對歐洲區域的電離層TEC 區域重構[12-13]；陳春等人根據foF2時間和空間相關性，通過克里金空間插值方法引入電離層空間距離、經度因子和緯度因子等參數實現了電離層TEC 區域重構[3]；劉瑞源等人提出了一種適用于中國地區電離層TEC 的短期預報方法，并定量分析了低緯站和邊緣站對區域重構的精度誤差影響[14]；然而通過克里金空間插值方法實現電離層TEC 區域重構過程中，區域重構的精度取決于模型對待估算點位和已知樣本點位空間位置及其空間相關性這兩者的反映程度[7].但隨之帶來的問題是，當克里金空間插值方法擬合變異函數時，傳統理論變異函數模型面臨函數曲線固定、空間細節變化無法反映以及模型選取人為主觀等問題[15].

為解決上述問題，本文提出一種可選的TEC 區域重構方法，從電離層TEC 實際變化趨勢出發，采用最小二乘支持向量機(least squares support vector machine,LS-SVM)擬合實驗變異函數，實現電離層TEC 區域重構.為驗證此方法的準確性，本文選用中國陸態網地基GNSS 臺站某時刻三組不同時刻穿刺點垂直總電子含量(vertical TEC,VTEC)值作為實測數據，同時選用普通克里金空間插值方法中的指數理論變異函數模型、球狀理論變異函數模型以及本文模型進行實驗.結果表明，本文提供的電離層TEC區域重構方法計算的均方根誤差(root mean square error,RMSE)和平均絕對誤差(mean absolute error,MAE)均小于其他兩種理論變異函數模型，插值精度最好，為電離層TEC 區域重構提供了一種可選的思路.

1 相關理論原理

1.1 克里金空間插值方法

克里金空間插值方法在有限的區域范圍內對區域化變量進行無偏最優估計.區域化變量以自身具有的隨機性特征和結構性特征為基礎，對相關性和連續性等要素特點進行空間描述，模擬地理現象空間分布的相關性和變異性，因此能夠挖掘區域化變量的空間結構和空間變化規律.同時借助變異函數，既能夠描述其隨機性變化過程，又能夠反映區域化變量空間結構性變化過程[15].

變異函數 γ(x,h)定義為區域化變量z(x) 在x軸 方向上，z(x)在點位x和x+h處變量值之差的方差一半，如式(1)計算：

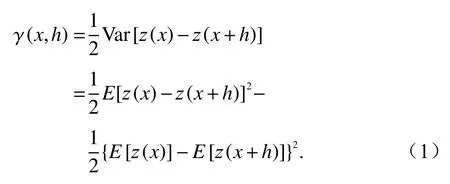
式中：Var[·]表 示方差；E[·]表示期望.

在二階平穩假設的情況下，對任意樣本點對的距離h有

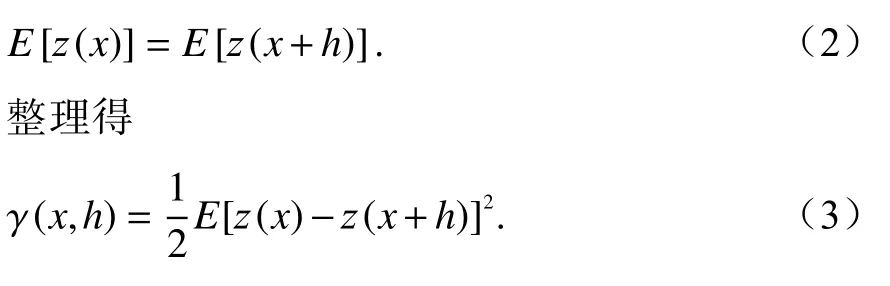
式(3)可理解為變異函數 γ(x,h)依賴于方向和距離兩個變量變化，倘若變異函數僅僅依賴于距離變化時，則 γ(x,h)可以寫為 γ(h)，同時稱 γ(h)為 各向同性.此時，離散樣本數據的實驗變異函數可以通過式(4)所示：

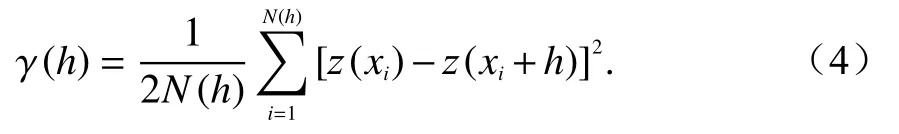
式中：h代表樣本點對的空間距離；N(h)代表當樣本點對距離為h時，所有樣本點對的總數量；z(xi)和z(xi+h)分別表示z(x)在點位xi和點位xi+h處的實際觀測值，即真實值.

克里金空間插值方法提供了包括線性模型、高斯模型、球狀模型、指數模型等在內的幾種常用理論變異函數模型[16].接下來以普通克里金空間插值方法為例，描述其實現的基本原理.

該方法實現空間估計主要滿足兩個基本條件：無偏性和估計方差最小，即：

求解得到如下方程組：

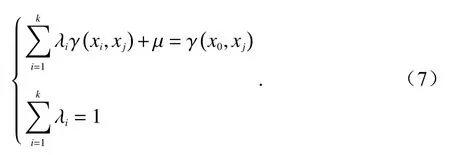
式中：λi為 空間權重系數，表示點位xi處的區域化變量z(xi)值對待估點位x0的貢獻程度；j=1,...,k，k為監測站點的總個數；為點位xi與點位xj距離下的實驗變異函數值；μ為拉格朗日乘子；為待估點位x0與點位xj距離下的實驗變異函數值.

將式(7)用矩陣展開，得到：

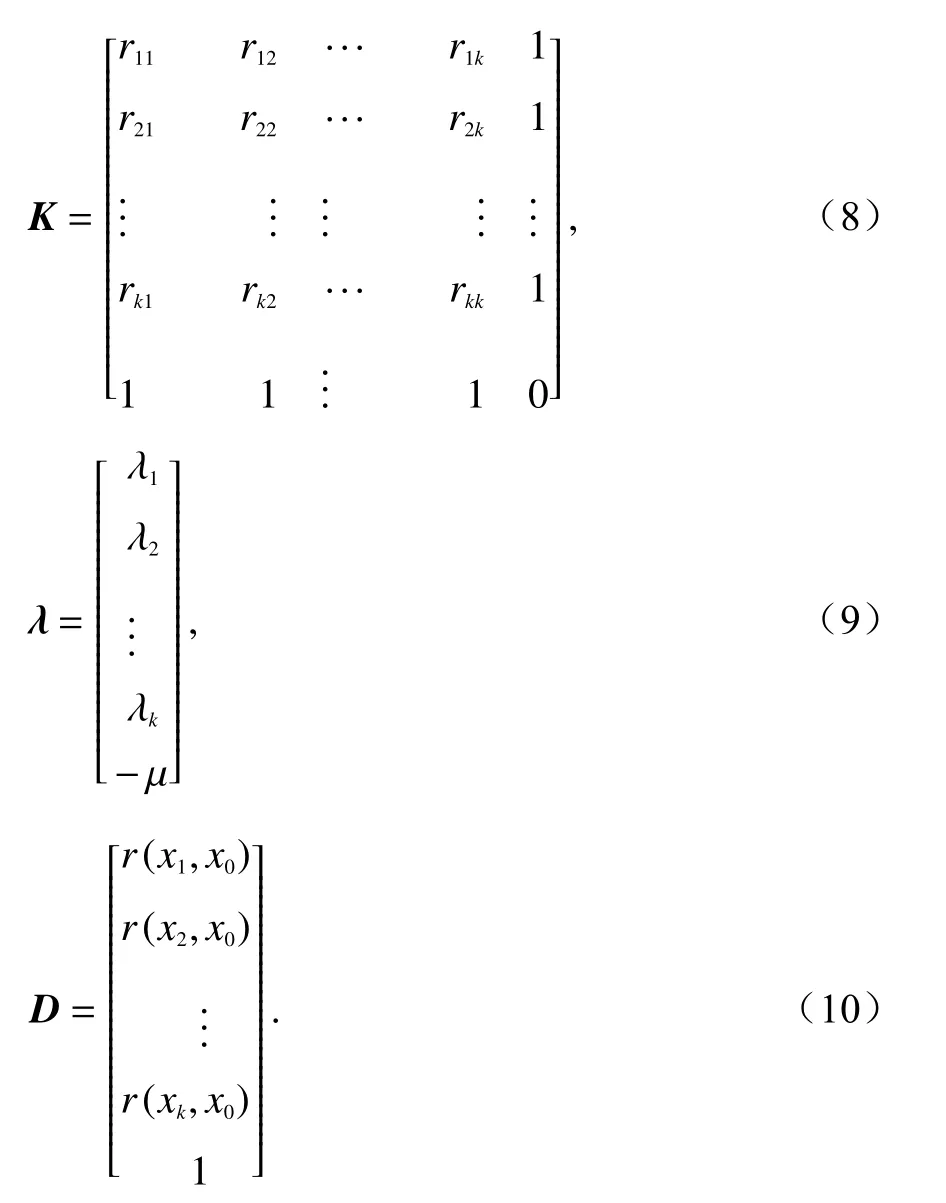
普通克里金空間插值方程為

解得

最終得到待估位置點x0處的區域化變量估計值z*(x0)：

式中：x1，...，xk為已知樣本點位；z(x1)，...，z(xk)為對應樣本點位的實際觀測值.

綜上所述，普通克里金空間插值方法基于無偏性和估計方差最小兩個原則，在此基礎上建立了含有約束條件的拉格朗日函數，插值結果的好壞完全取決于權重系數[8].通過約束條件和求極值問題解決待估位置點位區域化變量的無偏、最優估計[17].

1.2 LS-SVM

SVM 是由Vapnik 等人在20 世紀60 年代提出的一種有限樣本機器學習理論，以統計學習理論為基礎，SVM 模型不僅追求模型本身的泛化性能，且追求有限個樣本條件下的最優解[18].SVM 模型構建過程中，以結構風險最小化為基礎，主要用于處理小樣本、高維數、非線性、局部最優解等問題.LS-SVM作為SVM 演變的一種類型，其原理是計算損失函數時，以平方和誤差損失函數取代Vapnik 的ε 不敏感損失函數，同時構建等式約束條件[19-20]，計算原理如下：

給定N個樣本數據集 {其中第m個 輸入xm對應的輸出值為ym，回 歸函數f(x)的基本形式如式(14)所示：

式中：ω為權系數向量(列向量)；φ(x)為輸入空間到特征空間的映射函數，即低維空間向高維空間轉化的映射函數；b為常數項.

模型優化函數如式(15)所示：

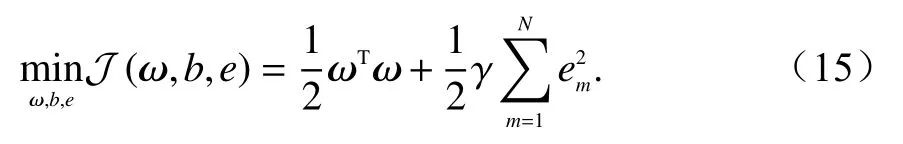
對應得到

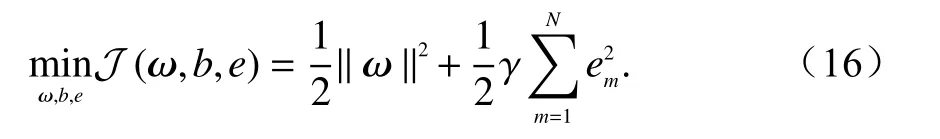
同時，上述公式也需滿足以下等式約束條件：

綜合上述條件，構建含有約束條件的拉格朗日函數，基于KKT(Karush-Kuhn-Tucker)條件，求解方程組，過程不再贅述.

最終回歸函數模型f(x)如下：

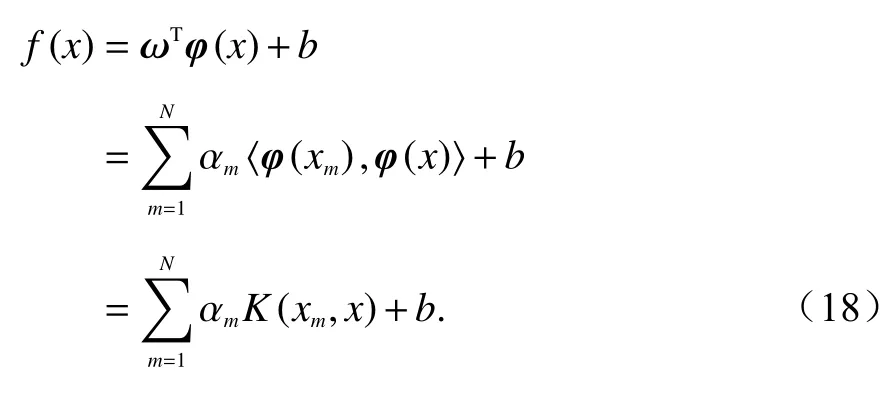
式中：αm表示拉格朗日乘子；K(xm,x)表示核函數.

2 計算流程

通過本文方法實現電離層TEC 區域重構方法，步驟如下：

步驟一：通過已知監測站點的地理坐標構建該區域網格化坐標點及范圍.根據已知站點的地理坐標經度和緯度，以經度的最小值和最大值構建網格區域的長邊，以緯度的最小值和最大值構建網格區域的寬邊，完成區域網格化坐標點及范圍的創建.

步驟二：借助離散變異函數式(4)，得到所有站點電離層TEC 樣本點對的實驗變異函數值，若實驗變異函數值較多則進行分組操作，便于后續擬合實驗變異函數.

步驟三：采用LS-SVM 擬合實驗變異函數值，得到理論變異函數模型.通過LS-SVM 與克里金空間插值相結合，采用LS-SVM 擬合實驗變異函數，能夠更精確地刻畫變異函數，反映電離層TEC 空間變化趨勢.

步驟四：根據式(7)建立方程組求解權重系數 λi.構建含有約束條件的拉格朗日函數，通過步驟三得到理論變異函數模型及其他參數，求解權重系數 λi.

步驟五：根據式(13)計算待估位置點的電離層總電子含量z*(x0)，即實現了網格內所有待估位置點電離層總電子含量無偏、最優的估計.

3 實驗分析

3.1 精度誤差指標

為檢驗本文提出的電離層TEC 區域重構方法，借助RMSE 和MAE 兩個精度誤差指標[21].RMSE 反映的是靈敏度變化和可能存在的極值誤差效應，MAE 反映的是總體精度誤差.兩個精度誤差指標數值越小，表明電離層TEC 區域重構效果越好.RMSE和MAE 的定義如下：

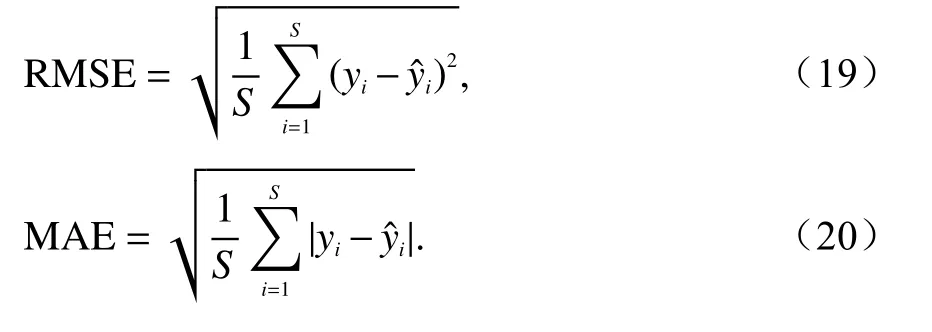
式中：S代表待估位置點的總個數；待估位置點的電離層TE C 真實值為yi；待估位置點的電離層TEC 估計值為

3.2 實驗數據

以中國陸態網地基GNSS 臺站三組不同時刻穿刺點觀測值作為實驗數據.采用文獻[22]中方法對數據進行預處理得到斜向總電子含量(slant TEC,STEC)，再通過薄層模型(single layer model,SLM)映射函數[23]轉化因子計算得到VTEC值，三組數據VTEC 分布如圖1 所示.其中，(a)表示2017-09-05T14:00:00UT(第一組)穿刺點VTEC 空間分布，(b)表示2017-09-07T03:31:00UT(第二組)穿刺點VTEC 空間分布，(c)表示2017-09-10T06:18:30UT(第三組)穿刺點VTEC 空間分布.

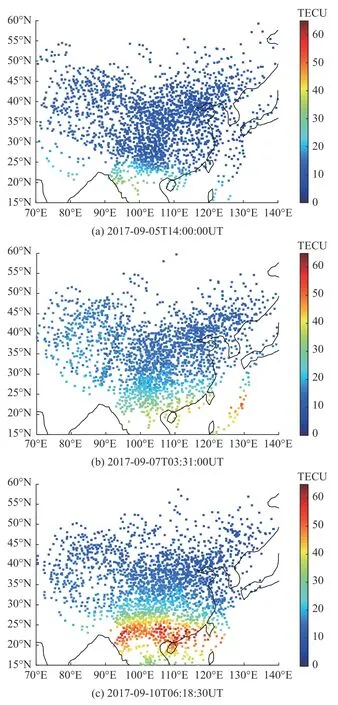
圖1 不同時刻穿刺點VTEC 空間分布Fig.1 The schematic of puncture points VTEC spatial distribution at different times

同時為對比各組數據理論函數變異模型計算得到的MAE 和RMSE 兩類評價指標誤差，將不同時刻穿刺點VTEC 值劃分為插值數據和測試數據.隨機均勻抽取樣本，通常插值數據占總樣本數據的75%，測試數據占總樣本數據25%，同時兩者數據不重復，以滿足計算過程的獨立性[18].各組數據分類個數如表1 所示.

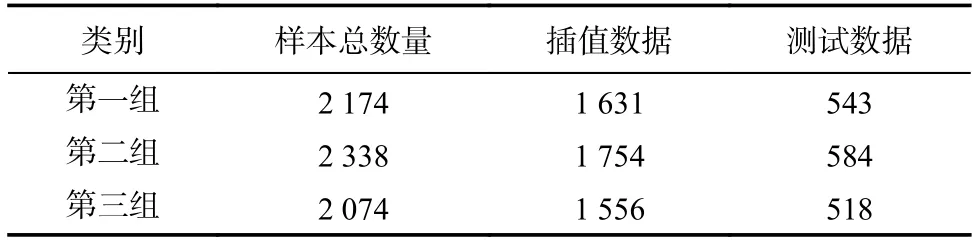
表1 三組數據樣本類別及數量信息Tab.1 Three groups of data sample category and quantity information

區域重構范圍為70～140°E、15～55°N，基本覆蓋中國大陸區域，重構數據的網格空間分辨率為0.5°×0.5°.

3.3 實驗結果

普通克里金空間插值方法中理論變異函數模型選用指數理論變異函數模型和球狀理論變異函數模型，用于對比本文方法實現的電離層TEC 區域重構效果.圖2 給出實驗過程中實驗變異函數的擬合曲線(以第二組數據為例).明顯可以看出，LS-SVM 理論變異函數較好地擬合了所有實驗變異函數值，整體擬合曲線符合電離層TEC 數據本身的空間變化特征，展現了數據本身的空間變化趨勢.

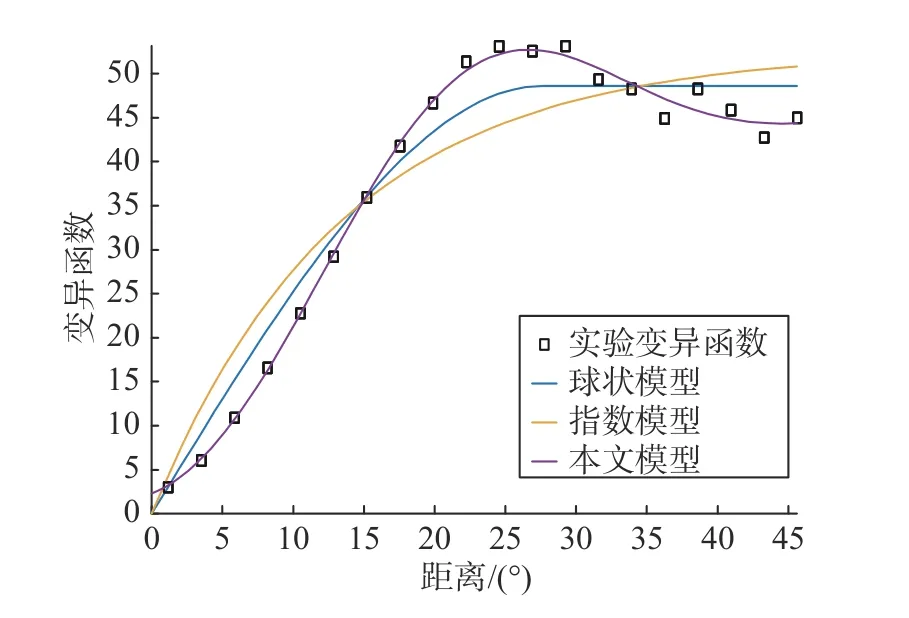
圖2 變異函數擬合曲線Fig.2 Variogram fitting curve

圖3、4 和5 分別為三組數據電離層TEC 區域重構效果.

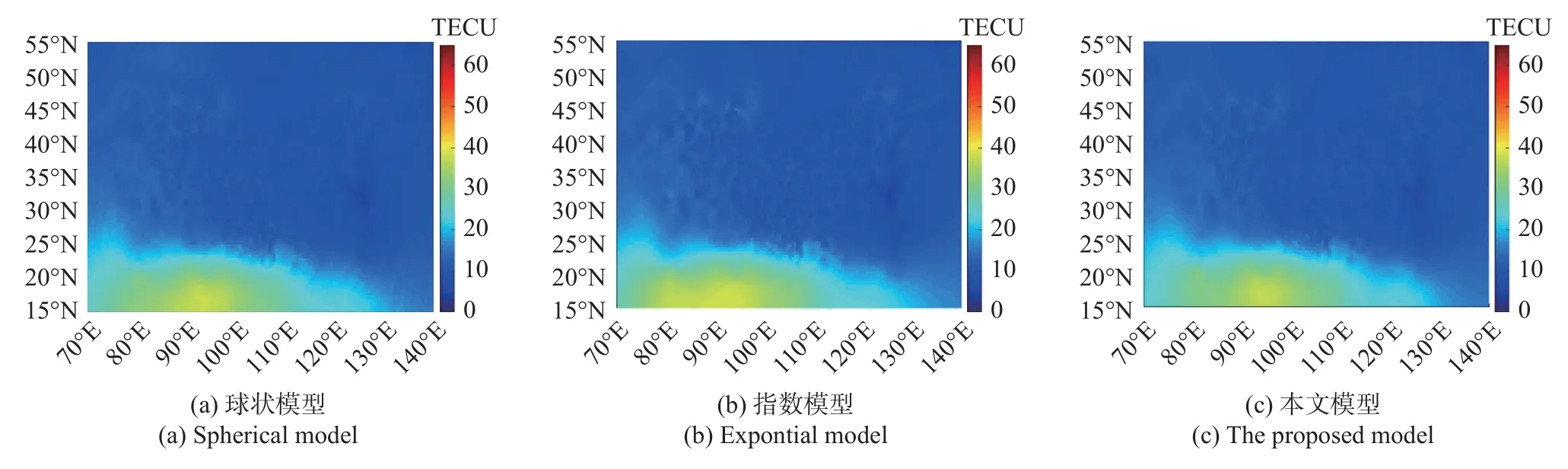
圖3 2017-09-05T14:00:00UT 電離層TEC 區域重構效果Fig.3 The effect diagram of ionospheric TEC region reconstruction at 14:00:00UT on September 5,2017

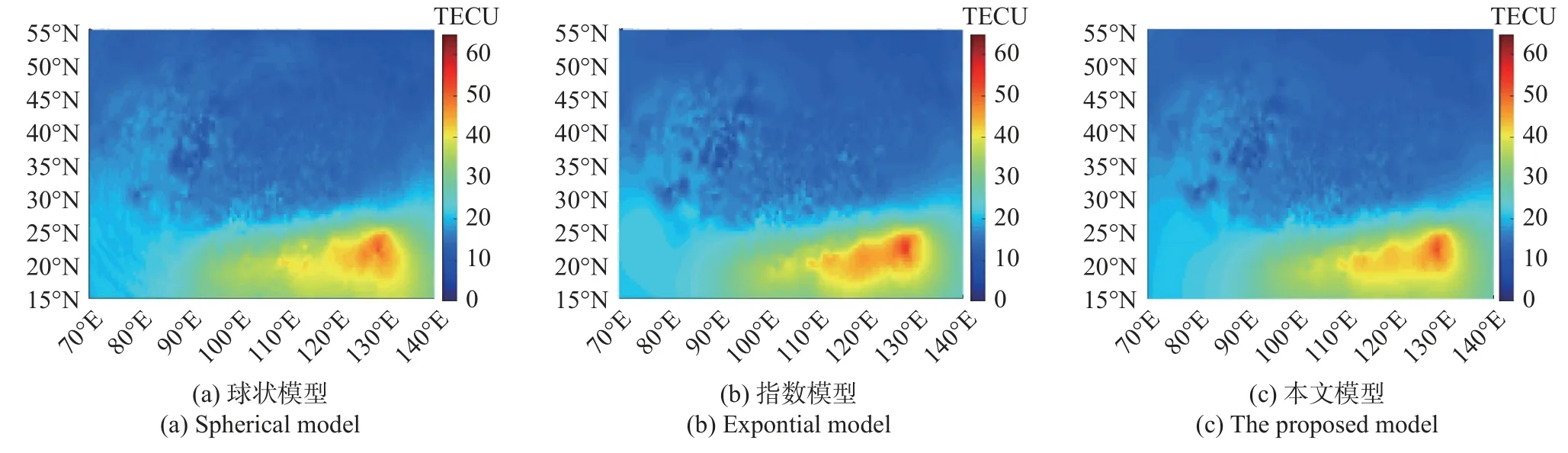
圖4 2017-09-07T03:31:00UT 電離層TEC 區域重構效果Fig.4 The effect diagram of ionospheric TEC region reconstruction at 03:31:00UT on September 7,2017

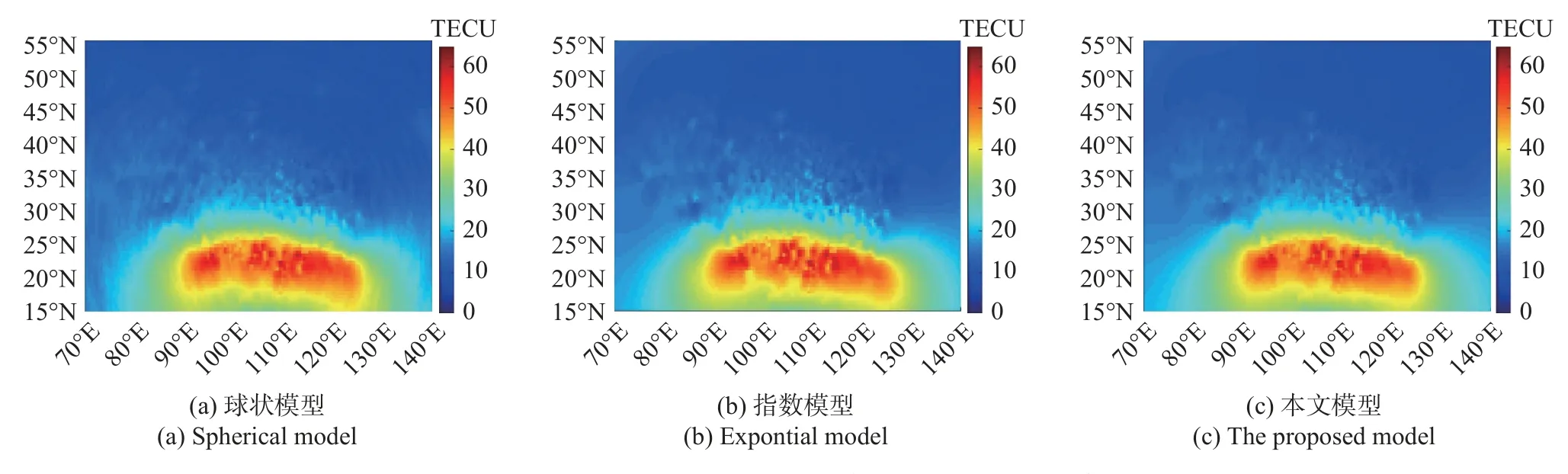
圖5 2017-09-10T06:18:30UT 電離層TEC 區域重構效果Fig.5 The effect diagram of ionospheric TEC region reconstruction at 06:18:30UT on September 10,2017

從圖3～5 可以看出，對比三種方法重構出來的電離層TEC 分布結果，LS-SVM 理論變異函數模型實現的區域重構效果大致符合通過克里金空間插值方法球狀理論變異函數模型和指數理論變異函數模型重構的效果，三者空間變化趨勢相近，空間變化呈現整體變化平緩、低緯地區偏高、高緯地區偏低的趨勢，符合電離層TEC 空間分布特征.因此保守地認為，本文方法的確可以作為一種可選的電離層TEC區域重構方法.

從TEC 區域重構結果分析，TEC 值變化呈現從低緯地區向中高緯地區逐步銳減的趨勢，本文選用的三組數據，包括夜間VTEC 和日間VTEC.第一組數據選用夜間VTEC，取值范圍[0,35] TECU，變化平緩；第二組和第三組數據選用日間VTEC，取值范圍[0,65] TECU，變化劇烈.三組實驗數據整體時間變化趨勢基本符合電離層TEC 的空間變化趨勢，與文獻[24]通過改進克里金空間插值方法給出的該區域電離層TEC 重構結果基本一致.

同時，為定量對比三種方法得到的區域重構結果精度誤差，分別統計了不同理論變異函數模型下的RMSE 和MAE，如表2、表3 和表4 所示.

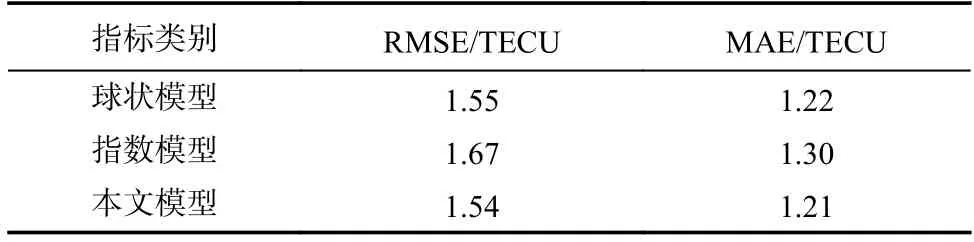
表2 第一組數據精度誤差對比Tab.2 Accuracy error comparison (the first group)

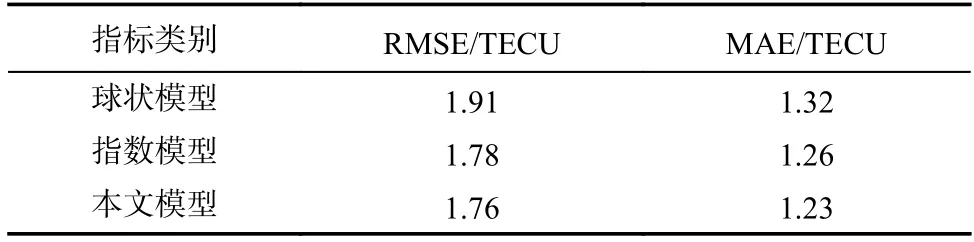
表3 第二組數據精度誤差對比Tab.3 Accuracy error comparison (the second group)

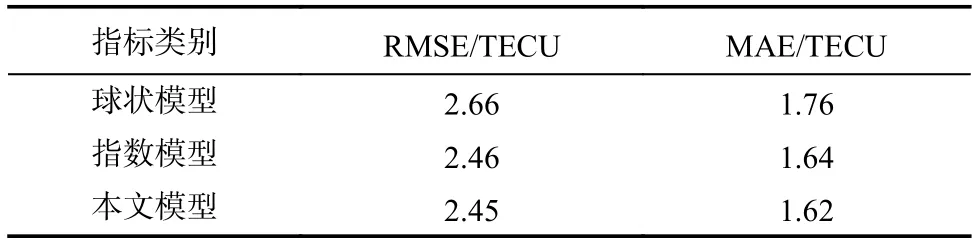
表4 第三組數據精度誤差對比Tab.4 Accuracy error comparison (the third group)

表2～4 直觀地顯示出不同理論變異函數模型計算得到的電離層TEC 區域重構結果，傳統克里金插值擬合模型中，指數理論變異函數模型誤差小于球狀理論變異函數模型；LS-SVM 理論變異函數模型RMSE 誤差分別為1.54 TECU、1.76 TECU 和2.45 TECU，MAE 誤差分別為1.21 TECU、1.23 TECU 和1.62 TECU.因此，這三種區域重構方法中，本文方法效果最好.同時，對比分析表2～4，三組實驗數據精度誤差存在差異性，作者分析認為，該差異性主要由數據本身的空間屬性變化差異性引起.白天VETC值差異性明顯，同時該研究區域中低緯地區處于電離層異常區域，梯度變化十分劇烈，引起的極值變化較多，因此精度誤差偏大.相反地，夜間VETC 值變化則較為平緩且極值點較少，誤差精度反而較低.

4 結論

電離層TEC 區域重構常采用克里金空間插值方法，但克里金空間插值方法擬合變異函數時，傳統理論變異函數模型面臨函數曲線固定、空間細節變化無法反映以及模型選取人為主觀等問題，為解決諸如此類的問題，本文提出了一種可選的電離層TEC區域重構方法.這種方法通過結合電離層TEC 數據的空間變化特征，能夠更精確地刻畫變異函數，反映電離層TEC 數據在空間中的實際變化趨勢，從而在一定程度上提高了電離層TEC 區域重構的精度.

需要與讀者說明的是，本文提出的這種電離層TEC 區域重構方法主要基于兩方面考慮：1)電離層TEC 數據本身是一種具有地理空間特性的區域化變量，在變化過程中與周圍鄰域的位置點及位置數據產生作用，體現為空間屬性的相關性或相似性特征，因此適合采用克里金空間插值方法實現區域重構；2)電離層TEC 區域重構過程中，理論變異函數模型擬合實驗變異函數離散點，如何實現更精確的擬合和更優良的泛化性能，是追求無偏性和最優解的目標.通過真實數據進行仿真驗證，結果表明該方法在一定程度上可以提高插值精度，即提高電離層TEC 區域重構的準確性，為研究此領域的作者提供一種思路供大家參考借鑒.

但同時值得思考的是，實驗過程中也存在一些需要后續繼續研究的內容：不同樣本數據即電離層TEC 數據計算得到的區域重構精度不盡相同，作者分析認為一方面是數據本身可能存在特殊性，另一方面LS-SVM 模型本身的泛化性能會根據數據的不同而存在差異性.后續研究不僅需要更多的數據參與實驗驗證，同時引入其他人工智能方法實現不同方法之間的對比提高.

致謝：本文GNSS 觀測數據從中國大陸構造環境監測網絡(Crustal Movement Observation Network of China，CMNOC)獲取，作者在此表示感謝.本工作得到國家重點研發計劃(2018YFF01013702 和2018 YFB0505100)的資助.