智能網聯混合交通流穩定性解析方法綜述

蔣陽升 ，顧秋凡 ，姚志洪

（1. 西南交通大學交通運輸與物流學院，四川 成都 610031；2. 西南交通大學綜合交通大數據應用技術國家工程實驗室，四川 成都 611756；3. 西南交通大學綜合交通運輸智能化國家地方聯合工程實驗室，四川 成都 611756）

交通流穩定性是衡量交通系統應對擾動平穩運行的重要指標. 對于道路上處于平衡態的跟馳車隊，若其中一輛或幾輛車改變駕駛行為（如加減速、急剎車、變道等）將影響后方車輛的駕駛行為，進而在車流中引起車速波動. 若這種波動的幅度逐漸放大，將演化為車隊系統的失穩；反之，若隨著時間推移，波動幅度衰減并趨于零，最終交通流恢復到平衡態，系統穩定[1-2].

一般地，按照系統受到的擾動幅度的大小可分為非線性穩定性（nonlinear stability）分析和線性穩定性（linear stability）分析. 非線性穩定性分析側重于研究大擾動影響下的交通流穩定特性，大多采用攝動法推導微觀或宏觀交通流模型的沖擊波方程，來描述交通波特性，其推導條件相對嚴格且復雜. 與線性穩定性相比，非線性穩定性通常不具備解析性.

對于線性穩定性分析，通常分為兩種類型，即局部穩定性（local stability）分析和隊列穩定性（string stability）分析. 局部穩定性主要研究連續兩輛車組成的子系統的穩定性，即研究跟馳車輛對前車擾動的響應，屬于交通流的局部行為. 而隊列穩定性主要考慮擾動在車隊系統中的傳播，研究擾動在車流上游的傳播幅度[3-4]. 盡管車隊中某些子系統的局部穩定性存在，但并不能保證整個系統的車隊隊列穩定，無法確定車隊中的車輛是否將干擾信號放大并將其傳遞給上游，并由此導致隊列不穩定[5]. 在實際交通運行系統中，駕駛員受到的干擾通常較小，且針對某一輛車在擾動發生后隨著時間的推移能夠達到穩定狀態，所以局部穩定性在合理的駕駛約束條件下易得到保證[4,6]. 因此，大多數文獻側重于研究隊列線性穩定性.

與人工駕駛車輛（human driven vehicle，HDV）相比，智能網聯汽車（connected automated vehicle，CAV）能夠實現信息共享和精準控制優化. 同時，CAV 間保持較小的車頭時距，具備更短的反應時間，因此，能夠維持更穩定的運行狀態[7]. 然而，智能網聯相關設施設備的升級換代是一個相對漫長的過程，實現完全智能網聯環境仍需一定時間. 研究表明，預計2045 年城市道路上的L4 級別的CAV 滲透率僅能達到24.8%[8]. 由于HDV 的存在，CAV 的決策過程將更為復雜，故由HDV 和CAV 組成的混合交通流在穩定性方面與單一車流存在一定的差異性. 此外，混合車隊隊列穩定性分析是研究智能網聯背景下相關問題的理論基礎，故其逐漸成為國內外學者的研究熱點.

鑒于近幾年關于智能網聯環境下的混合交通流穩定性分析研究較多，本文認為有必要對該領域的相關研究成果進行全面篩選、梳理、總結和討論，為后續研究提供參考. 本文首先介紹了跟馳模型的相關概念以及隊列穩定性判定的基本準則；從控制理論的角度回顧了關于車隊系統隊列線性穩定性的經典解析研究方法；在此基礎上，對當前智能網聯環境下的混合交通流穩定性問題的研究進行了梳理和論述；基于上述理論研究，回顧了在車隊隊列控制等方面的工程應用；最后，討論了未來的研究方向.

1 相關概念與理論基礎綜述

1.1 跟馳模型

在車輛行進過程中，每一輛車動態地與其他車輛耦合，因此，車隊系統可認為是一個大的動力系統. 由于車輛間的耦合作用，利用跟馳模型分析車輛列隊行駛時，前車的擾動對后車的影響隨時間和空間的演變趨勢是一種常用的研究方法. 跟馳行為主要描述了車輛在單一車道上行駛時，后車根據前車駕駛狀態調整自身運動的微觀駕駛行為，具體跟馳情況如圖1 所示. 圖中：xn(t) 和vn(t) 分別為車輛n在時刻t的位置和速度； Δxn(·) 為車輛n與前車（車輛n-1 ） 的車頭間距；hn(·) 為車輛n與前車的車間距；l為車身長.

圖1 車輛跟馳運動示意Fig. 1 Schematic of car-following motion

廣泛應用的跟馳模型有智能駕駛員模型（intelligent driver model，IDM）[9]、最優速度模型（optimal velocity model，OVM）[10]和全速度差模型（full velocity difference model，FVDM）[11]等. 跟馳模型一般通過建立目標車輛加速度與自身車速、前車速度差、前車車間距的非線性關系來描述車輛的跟馳狀態，如式（1）所示.

式中：an(·) 為車輛n的加速度； Δvn(·) 為車輛n與前車的速度差；f(·) 為特定跟馳模型的函數形式.

對于處于穩定狀態的交通流，車輛以車隊形式勻速行駛，每輛車的行駛狀態一致，擁有相同的速度和車間距，速度差和加速度均為0. 因此，平衡狀態下交通流中每輛車的跟馳運動方程為

式中：he和ve分別為交通流在平衡狀態下的車間距和速度.

假設車隊系統在穩定狀態下出現輕微擾動，擾動與速度、車間距之間的關系如式（3）、（4）所示，而加速度的變化體現在跟馳模型中. 由此，交通流隊列穩定性的分析就是研究擾動量在車隊系統中每輛車間的演變規律，yn(t) 和un(t) 分別為車輛n在時刻t的間距擾動和速度擾動.

交通流系統是一個非線性、強耦合的復雜系統，大多跟馳模型為非線性函數形式，研究其性質相對困難. 以通用的跟馳模型式（1）為例，采用一階泰勒在平衡點 (he,ve,0) 附近展開進行線性近似，略去高階項，如式（5）所示.

式（5）可進一步轉化為

此外，對式（3）求導得到車間距與速度之間的關系， 如式（7）所示.

車隊系統的狀態方程如式（8）所示.

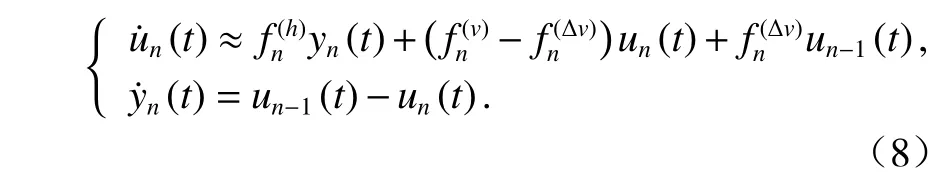
式（8）描述了車隊系統受到擾動后偏離平衡點時車間距、速度和加速度的變化特性. 現有系統穩定性的研究方法大多基于系統的線性微分方程組得到描述系統變化特性的解，或得到系統前后狀態的關系式，從而進一步判定系統的狀態變化.

1.2 穩定性判定準則

對于一個車隊系統，當由頭車傳出的擾動在每個跟馳對內不斷衰減時，這樣的車隊系統具有隊列穩定性，用數學方法[12]表示為

式中： εm(t) 為車輛m（ 1 ≤m≤n） 在時刻t受到的擾動； ‖ εm‖∞=max{|εm(t)|} ，表示車輛m在整個時域內受到擾動的最大值.

若不滿足式（9），系統是不穩定的. 顯然隊列穩定需要滿足一定的條件，即能保證對頭車的任何干擾不影響跟馳車輛的速度和位移[13-14]. 對車隊隊列的穩定性分析就是要獲取多情景下車隊隊列保持穩定性的邊界條件.

2 車隊隊列線性穩定性條件經典解析方法

目前混合交通流穩定性分析方法主要分為兩個方面：一方面從控制理論的角度結合系統穩定性的概念進行理論推導分析；另一方面則是采用現場實驗或仿真實驗[15-21]模擬混合交通流運行場景，研究特定環境下車流穩定性變化規律. 如Schakel 等[15]設計了一個在4 km 單車道上的現場測試實驗，收集HDV、自適應巡航控制車輛（adaptive cruise control，ACC）、協同自適應巡航控制車輛（cooperative adaptive cruise control，CACC）的行駛軌跡來判斷交通流對擾動的響應是否穩定，結果表明，在50%的CACC滲透率下，交通波能得到快速吸收. Chen 等[16]模擬了ACC/HDV、CACC/HDV和ACC/CACC/HDV三種混合交通流場景，研究結果表明，在混合交通流中引入ACC 和CACC 車輛可以改善交通流穩定性，提高道路通行能力.

本文更關注于穩定性分析的理論研究，以下回顧梳理了車隊隊列線性穩定性的基本解析方法：特征方程法和傳遞函數法. 其中，特征方程法是研究車隊隊列系統線性穩定性的常規方法，而傳遞函數法則研究了交通流內部擾動的傳遞關系.

2.1 特征方程法

特征方程法的思想是通過求解擾動的數學表達式來評估擾動的增長速度. 一般地，直接求解上述微分方程組較為困難，因此，通常采用根提取法，即事先假設解的基本形式，代入原方程組間接獲得.

在隊列穩定性研究中，設第n輛車受到的間距擾動和速度擾動分別如式（10）、（11）所示.

式中：yn,0和un,0分別為間距和速度的初始擾動；為獨立于n、t的復常量； λ=σ+jφ ，為復合增長率（實部 σ 為波動幅度的增長速率，虛部 φ 為角頻率，即駕駛員通過一個完整的交通波的時間為 2 π/φ ）；φ為給定時刻交通波從一輛車到下一輛車的相移[22].

將式（10）、（11）代入式（8），得到系統矩陣為

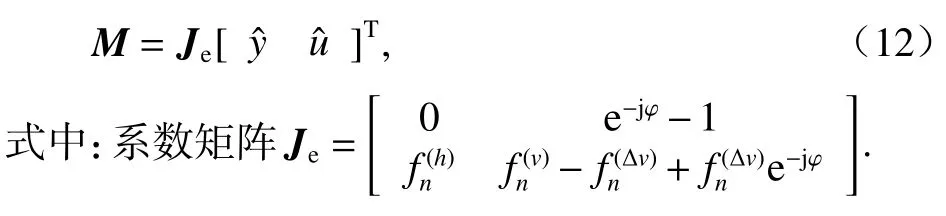
因此，系統的特征方程為

式（13）可轉化為

對于式（14）解一元二次方程，根為

根據李雅普諾夫第一定理，對于所有的 φ ，當Re(λ±)≤0，可認為車隊系統是穩定的[6]，此時，系統所有特征值全部位于復平面的左半部.

2.2 傳遞函數法

利用傳遞函數法的基本思想是觀察系統輸入和輸出之間的頻率響應[23]. 系統的傳遞函數表征了被研究系統的動態性能. 對于車隊這一特殊系統，可將其分解為有限個子系統，每個子系統為車隊中連續的跟馳車輛對. 如果將車輛n-1 的速度擾動un-1(t)作為輸入信號，那么車輛n針對前車的擾動做出的加減速行為可看作相應的響應，也會產生一定的速度擾動，即產生輸出信號un(t) .

通過拉普拉斯變換用相對簡單的復頻域代數方程取代復雜的時域微分方程[24]，并利用傳遞函數的幅度分析車隊的穩定性. 圖2 反映了車隊系統中車輛n-1 與車輛n之間的速度擾動傳遞函數關系. 圖中：Un(s)=L[un(t)] ， L(·) 為拉普拉斯變換；Gn(s)為速度擾動經歷車輛n時的傳遞函數.

圖2 速度擾動傳遞函數Fig. 2 Transfer function of velocity disturbance

分別對式（6）、（7）進行拉普拉斯變換得

式中：Yn(s)=L[yn(t)]

.

由式（16）、（17）可得

在交通流中，擾動沿著上游依次傳播，交通流的總傳遞函數等于各個跟馳車輛對間傳遞函數的乘積. 因此，在混合交通流中，車輛n（n≥2） 與頭車的擾動傳遞關系如式（19）所示.

顯然，要保證車隊整體線性穩定性，那么車隊中每一輛車的速度變化需滿足在頭車速度變化基礎上減弱. 因此，將式（19）中的傳遞函數由拉普拉斯域轉變至頻率域，根據傳遞函數理論，混合交通流的穩定性判定條件為

式中：ω為頻率.

而對于單一交通流中的任意車輛m，令Gm(s)=G(s)，式（20）可簡化為

因此，單一交通流的隊列線性穩定性條件為

即

綜上，特征方程法主要利用對系統特征方程的根提取，直接得到擾動的增長幅度，適用于一些簡單的跟馳模型，復雜跟馳模型的計算求解具有一定的難度. 而傳遞函數法依托于拉普拉斯變換構建了交通流中任意車輛之間的擾動傳遞關系，以傳遞函數的大小作為穩定性判斷依據，是研究混合交通流隊列穩定性的有效方法.

3 智能網聯環境下混合交通流穩定性分析

目前大部分研究構建的混合交通流模型主要用三個模型來描述車輛的跟馳運動，分別是傳統跟馳模型、考慮時延的跟馳模型和考慮多前車駕駛信息反饋的跟馳模型，對其穩定性的分析集中在穩定性條件的研究.

對于常規駕駛環境下的交通流穩定性研究主要考慮駕駛方式和車輛構成的異質性[25-32]. Ward[33]最早于2009 年提出了在常規駕駛環境下“小車-大車”的混合交通流穩定性解析框架，如式（24）所示.

隨后，Ngoduy[34]利用特征方程法將該結果推廣到智能網聯環境下的混合交通流中，并得到了廣泛應用[35-42]. 如Talebpour 等[35-36]依據式（24）研究了CAV 的通信能力和通信范圍對混合交通流穩定性的影響. 秦嚴嚴等[37-38]研究了智能網聯環境下混合交通流穩定性的基本問題，并進一步分析了安全性、通行能力、基本圖等問題.

根據式（24），以經典跟馳模型為例，對于存在HDV 和CAV 兩種車輛類型的混合交通流，其隊列線性穩定性條件的一般表達式為

式中：PCAV為混合交通流中CAV 滲透率；（） 、（）、（）分別為CAV （HDV）車輛的跟馳模型在平衡點 (he,ve,0) 對速度、速度差和車間距的偏導數值.

在式（25）中，每一個PCAV和平衡態速度值對應一個穩定性值，若該值大于等于0，則認為在當前條件下混合交通流是穩定的，反之則不穩定.

圖3 以IDM 模型為例，對式（25）的混合交通流穩定性條件進行數值分析. 混合交通流隨著平衡態速度的增加呈現從穩定到不穩定再到穩定的變化趨勢. 隨著PCAV的增加，速度穩定區間不斷擴大，由此說明CAV 有助于提高混合交通流的穩定性.

圖3 經典跟馳模型下的穩定性Fig. 3 Stability of basic car-following model

此外，除了上述利用穩定性條件判別式（24）外，以下將從三類跟馳模型出發，通過文獻綜述對目前其他方向的穩定性研究進行系統的回顧與討論，如表1 所示.

表1 智能網聯環境下的混合交通流穩定性分析文獻總結Tab. 1 Literature review on stability analysis for mixed traffic flow with connected automated vehicles

3.1 經典跟馳模型

經典跟馳模型描述了連續車輛之間的縱向運動關系，不考慮其他因素的影響，基本形式如式（1）所示. 早期學者圍繞經典跟馳模型進行了混合交通流穩定性廣泛的擴展研究.

Wang 等[43]分析了由ACC 與HDV 組成的混合交通流穩定性、魯棒性和安全性等問題. 首先指出了在固定時間間隔車間距策略下，交通流的穩定性取決于邊界條件；從基于流量-速度關系的李雅普諾夫穩定性定義的角度說明了混合交通流穩定性的準則函數；該研究表明：如果初始狀態在穩定狀態簇的邊界內，且狀態轉移滿足穩定判據，交通流將保持穩定，否則失去穩定，進入擁堵狀態. 而Shaw 等[44]提出了前后車定間距跟馳策略，該策略與Wang 等[43]的固定時間間隔車間距策略的區別在于略去了在固定時間內的車輛位移；將智能網聯環境下的車輛分為三種車型：低帶寬、中帶寬和高帶寬車輛，并為每種車型設計了一個單獨的控制器；根據傳遞函數推導了該策略下的隊列穩定性充分性條件，分析了任意車隊規模和任意車型排序下的混合交通流穩定性問題. 此外，Wang 等[45]分別開發了ACC和CACC 控制策略，將線性穩定性方法擴展到協作駕駛環境中，討論了車隊系統的穩定特性；結果表明，所提出的ACC 模型是無條件局部穩定的，CACC 模型是絕對隊列不穩定的；該結果為駕駛員輔助系統的開發提供了指導，并為ACC 和CACC系統對交通流運行的影響機理提供了新見解.

上述研究[43-45]主要關于控制策略下的混合交通流穩定性問題，目前還存在一部分研究注重從交通流理論出發，研究混入智能網聯汽車后隊列穩定性的變化. 如Wang 等[46]關注到當CACC 車輛跟馳未配備通信設備的HDV 車輛時會退化為ACC 車輛的現象，首次研究混有CACC、ACC 和HDV 車輛的混合交通流穩定性問題；將式（24）轉化為與ACC車輛和CACC 車輛比例有關的一元二次方程. 通過研究二次函數曲線的基本性質，結合6 個研究場景，從理論上分析了不同CACC 滲透率下交通流穩定性；研究發現，CACC 系統的退化導致隊列穩定性的顯著惡化. 王昊等[47]同樣基于CACC 車輛功能降級退化機理，提出了一種網聯車混合交通流漸進穩定性解析方法；基于傳遞函數理論，應用跟馳模型推導了擾動在交通流中傳播時的傳遞函數，建立該混合交通流漸進穩定性的一般性解析框架，并進行小擾動下的數值實驗；結果表明，所建立的解析框架可計算任意速度下保證混合交通流穩定的網聯車滲透率閾值.

目前描述車輛跟馳行為的模型大多基于理想假設，往往與車輛實際運動特性存在差異. 因此，針對這一缺陷，Li 等[48]根據現場實際數據探究CAV 的運動過程，通過數據挖掘技術，提出了一種改進的IDM 模型（modified intelligent driver model，MIDM），并對改進后的模型參數進行標定；利用特征方程法得到了車隊的線性穩定性條件，仿真結果表明：MIDM 中參數對系統穩定性的影響與理論分析一致，即在正確響應安全信息的前提下，CAV 具備減少級聯制動事件的能力，能改善系統穩定性.

上述研究[46-48]所采用的微觀跟馳模型在某種程度上并未反映CAV 車輛的網聯特性. 不同于HDV車輛，CAV 車輛在合適的條件下將組成車隊共同行駛. 因此，Ngoduy[49]提出了一種描述智能網聯混合交通流運行特性的宏觀動力學模型，該模型基于Helbing 等[50]的廣義力模型通過矩量法導出；新模型中一定數量的CAV 車輛構成的隊列被看作獨立的“一輛車”，各個隊列相互跟馳，利用特征方程法推導出了線性穩定性條件，給出了一定參數下的穩定性曲線圖；分析結果表明，CAV 的組隊駕駛行為增強了交通流的穩定性.

3.2 考慮時延的跟馳模型

在實際駕駛過程中，后車對前車駕駛行為的響應并不是瞬間實現的，時延是影響車輛跟馳行為和交通流穩定性的重要因素[51]. 對于HDV，時延體現在駕駛員的反應時間上，主要來自駕駛員的生理感知和決策過程[52]. 而對于CAV，時延主要來自車輛在感知、決策計算和通信等方面的延遲[53].

考慮時延的跟馳模型將有限時延項納入經典跟馳模型中，如式（26）所示. 由式（26）可知，時延的存在導致后車無法根據前車在時刻t行駛狀態的變化做出響應.

式中： τn,h、 τn,v、 τn,Δv分別為車輛n對與前車車間距變化、速度變化和速度差變化響應的時延項.

類似地，對式（26）在平衡點 (he,ve,0) 處線性展開，忽略高階項，得到式（27）.

因此，考慮時延的車隊系統狀態方程組為

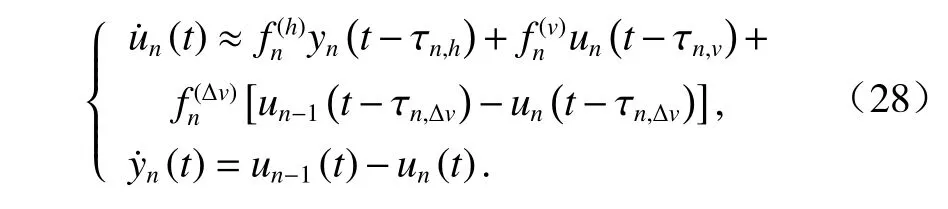
在早期考慮時延的混合交通流的研究中，時延項并未作為主要的研究對象進行單獨研究，而是體現在選用的跟馳模型中，并且大多為駕駛員的感知-反應時間. 如Bose 等[54]利用智能巡航控制模型研究由常規車輛和半自動車輛組成的混合交通流的穩定性；對于常規車輛采用Pipes 模型，該模型描述了駕駛員對前方車輛的刺激做出的反應；通過傳遞函數理論證明了半自動車輛在平穩瞬變過程中不會產生彈簧效應現象，能產生過濾前車的急加速響應，平穩改善交通流. Zhu 等[55]采用Bando 模型和改進的Bando 模型分別描述HDV 車流和AV 車流，在Bando模型中駕駛員的敏感度是對前車反應時間的倒數；對于AV，認為可以感知相鄰的前后車信息，引入平滑因子來平衡AV 車流中前后車車頭時距；通過特征方程法研究穩定域，并進行仿真模擬，研究不同靈敏度參數和平滑因子對混合交通流穩定性的影響；結果表明，靈敏度參數和平滑因子對穩定混合交通流具有積極作用.

文獻[34，56-60]明確了時延對混合交通流穩定性的影響. Ngoduy[34]針對由HDV 和CAV 構成的交通流，首先嘗試采用IDM 模型來推導考慮時延的混合交通流的穩定性閾值；結果表明，混合交通流中車隊的整體穩定性由各類別車輛對應穩定性參數的加權平均值決定，不受不同類別車輛相對位置的影響；而駕駛員的反應時間會破壞交通流的穩定性.Xie 等[56]改進了Ngoduy[34]的研究，建立了同時表征HDV 和CAV 跟馳特性的通用跟馳模型，利用特征方程法從理論上推導了混合交通流的線性穩定性條件，最終表達式與Ngoduy[34]的結論一致；相關實驗結果表明，混合交通流的穩定性與CAV 的滲透率和空間分布密切相關.

文獻[34，56]均未考慮到CAV 跟馳HDV 產生的功能退化現象，Yao 等[57]彌補了這一不足，討論了混合交通流中HDV、CAV 和退化的CAV （DCAV）這三種車輛類型的時延值；通過特征方程法得到了混合交通流的線性穩定性條件，該條件僅包含了HDV 的反應時間，忽略了DCAV 的通信時延；數值實驗結果表明，當CAV 滲透率增加到65%時，穩定性不受速度的影響.

Ngoduy[34]、Xie 等[56]和Yao 等[57]在研究方法上存在一定的相似性，均采用IDM 模型推導混合交通流穩定性條件，通過模型參數取值區分車輛的不同類型. 比如CAV 相較于HDV 擁有更大的起步加速度，更小的舒適減速度、安全時間間隔和靜止安全距離. 然而這些還不能完全反應CAV的駕駛特性，正如3.1 節提到的CAV 車隊的存在. 因此，Zhou 等[58]考慮了CAV 的連通性，以車隊強度表征CAV 組成車隊的可能性，利用傳遞函數法推導了考慮車隊強度和時延的混合交通流穩定性條件，側重于研究智能網聯車隊的最大規模與交通流穩定性的關系. 而Zhou 等[59]將混合車輛隊列看作一個由多個子系統組成的單一的互聯系統，其中子系統為隊列中所有可能的車輛序列；對于隊列穩定性的分析，提出了一種適用于各類車輛的通用傳遞函數，其范數可用來定量描述擾動阻尼比；但僅考慮了通信時延，且未研究時延的時變性和不確定性的影響.

將駕駛員操控HDV 的反應時間納入交通流穩定性分析已得到普遍認同，然而對CAV 的通信時延并未得到深入研究. 因此，許慶等[60]研究不同車聯網通信時延影響下，CACC 與HDV 構成的混合隊列系統的性能；從微觀跟車行為角度，基于頻域傳遞函數分析CACC 系統和通信時延過長產生的退化后的ACC 系統的隊列穩定性；實驗結果揭示，隨著通信時延增大，CACC 系統所需的隊列穩定最小跟車時距迅速增大，但與退化后的ACC 系統相比，仍具有在一定時延范圍內顯著降低交通擾動和削弱交通激波的能力.

3.3 考慮多前車駕駛信息反饋的跟馳模型

在常規的駕駛環境中，由于視野受限，駕駛員往往只能根據緊鄰的前車信息做出操作判斷. 而在智能網聯環境下，車輛能夠與通信范圍內的其他車輛實現相互協作，跟馳情景如圖4 所示. 圖中：hn,n-k(t)為車輛n與車輛n-k的車間距；k=1,2,···,K（K的大小取決于車輛n的感知范圍）.

圖4 多車交互跟馳運動示意Fig. 4 Schematic of multivehicle interactive car-following motion

考慮多前車駕駛信息反饋的跟馳模型基于CAV 的網聯特性，將目標車輛與多前車之間的間距差和速度差納入經典跟馳模型中. 該模型描述了目標車輛相對于前方多車的跟馳行為，同時考慮駕駛員的感知延遲和車輛的通信傳輸時延，如式（29）所示.

式中： Δvn,n-k為車輛n與車輛n-k的速度差；τn,n-k,h和 τn,n-k,Δv分別為車輛n對其與車輛n-k間間距變化和速度差變化響應的時延； φk和 ηk分別為相對車間距和相對速度的權重因子，一般地，越靠近車輛n的前車對車輛n信息獲取的貢獻越大，即φ1＞φ2＞···＞φK， η1＞η2＞···＞ηK.

由此，多信息反饋的車隊系統狀態方程組為

基于上述方法論，眾多學者對于考慮多前車駕駛信息反饋的跟馳模型從不同方面做了研究. 但由于該研究點較新，同時現有方法在求解多前車駕駛信息反饋的跟馳模型上存在一定的難度和復雜性，因此，這一方面的研究和應用較為分散和基礎. 相較于前兩類的跟馳模型，對于采用考慮多前車駕駛信息反饋的跟馳模型的車隊系統來說，在研究中更多的是將其看作一個緊密耦合的整體.

Jin 等[61]考慮駕駛員的反應延遲和前方多車信息，建立了混合交通流確定性模型；與Xie 等[56]的模型一樣，表征CAV 和HDV 駕駛行為的速度、速度差、間距差被統一到同一個公式中，通過決策系數區別不同的跟馳模式；研究了不同CAV 滲透率、駕駛員反應延遲和CAV 可獲取信息的前車數量條件下的穩定性. 而Wang 等[62]基于駕駛員記憶的最優速度模型，只引入了多輛前方車輛的速度，提出了一種新的考慮多前方車輛最優速度影響的跟馳模型（multiple vehicles changes with memory，MVCM）；采用特征方程法推導出MVCM 模型的穩定性條件，數值仿真結果表明，考慮更多前方車輛的最優速度能夠增強交通流的穩定性，但最佳前車數量為4.

從控制策略的角度，Ge 等[63]提出了一種CCC控制策略，其能通過車間通信接受前方多車的加速度信號，由此在原優化速度函數基礎上引入多前車的加速度值，建立考慮前車加速度反饋的跟馳模型；應用傳遞函數理論分析了不同通信結構下的混合交通流車隊穩定性，并進行了模型參數敏感性分析.Zhang 等[64]同樣提出了一種通用的CCC 設計框架，與Ge 等[63]不同的是，在該研究中每一輛車的加速度由控制器直接決定，并對CCC 車輛進行縱向動力學設計，研究多種連接結構和信息時延對網聯環境下車隊系統的動力學影響，利用傳遞函數理論推導了具有時延的車隊系統隊列穩定性的相關準則；研究結果表明，當通信時延低于某一閾值時，可通過增加CCC 車輛的滲透率和通信鏈路的數量來提高穩定性.

此外，有學者從車輛自身特性結構出發，將電子節氣門角度控制系統與縱向跟馳模型進行了關聯性研究. Ioannou 等[65]最早于1994 年開展了電子節氣門角度控制系統與車輛加速度輸出間的建模研究，由此產生了考慮多前車電子節氣門角度控制影響的智能網聯混合交通流穩定性研究. 如秦嚴嚴等[66]考慮多前車電子節氣門角度反饋，構建了關于CAV 車輛的特定跟馳模型，該模型納入了前方多輛車與目標車輛的電子節氣門角度差項，并為每一項賦上了相應的權重系數；應用一階泰勒公式線性化、傅里葉級數、長波理論等手段，推導出穩定性判別條件；數值仿真實驗表明，考慮前車數量越多，多前車反饋權重系數越大，模型的穩定性越好. 而文獻[67]基于FVDM 模型，引入車輛的閥門角度，應用集成速度與加速度的多前車反饋構建CAV 跟馳模型；考慮CAV 車輛空間分布的隨機性，將各類型局部車隊穩定性作為優化目標，以局部車隊頭車速度擾動為系統輸入，以尾車速度擾動為系統輸出，應用經典控制理論領域中的傳遞函數法推導局部車隊穩定性約束條件；與文獻[66]相比，該研究側重于研究不同前車數量即k=1,2,3 下局部車隊穩定域. Qin 等[68-69]同樣考慮多前車電子節氣門控制角度信息，但采用了帶響應時間的跟馳模型通用公式，建立了速度、加速度和通信時延相結合的多CAV 車輛反饋的擴展跟馳模型；利用傳遞函數理論，給出了由CAV 和HDV構成的車隊系統穩定性的一般性解析框架，分析表明CAV 在非線性水平上可以很好地抑制瞬時速度波動和周期性速度波動.

除了上述研究[61-69]，一些學者還研究了多前車駕駛信息反饋時延下的局部隊列穩定性、時變時延等問題. Qin 等[70]鑒于CAV 具有可監測前方多輛車、多重反饋和隨機空間分布的特性，從局部隊列的角度出發，提出了一種混合交通流穩定性分析方法；利用傳遞函數理論推導了局部隊列的穩定性準則，穩定性圖表明，通過控制CAV 反饋系數，可獲得各車速下保持隊列穩定性的最佳條件，但并不適用于CAV 滲透率較低的情形. Jia 等[71]建立了一種統一的多類車輛跟馳微觀模型，考慮了與CAV 前向通信的鄰車，探討了HDV 和CAV 之間的復雜交互作用；研究了多信息反饋和時延對混合交通流不穩定的聯合影響，從理論上得到了線性穩定性條件，并認為目標車輛與前導車輛的狀態誤差最終會限制在某個常數范圍內.

以上，從三類跟馳模型出發對智能網聯環境下的混合交通流穩定性研究進行了回顧與討論，可概括出以下結論：1） 對于經典跟馳模型，CAV 滲透率越高，隊列穩定性越好，說明CAV 對穩定混合交通流具有積極作用. 2） 時延是造成混合交通流不穩定現象的重要因素. 3） 考慮前方多輛車的駕駛信息能很大程度提高交通流的穩定性和效率.

4 實踐應用

在智能網聯環境下，實現車輛列隊控制，確保隊列中的車輛協同駕駛是最終目的. 而如何保證隊列穩定性，是智能車隊控制算法設計中的一個關鍵問題. 因此，對于智能網聯車輛隊列穩定性的所有理論研究最終將歸結到隊列縱向控制的實際應用中.

目前隊列穩定性理論研究廣泛應用于車輛的控制器設計. 美國的PATH 研究項目在過去15 a 的時間里發展了三代貨車縱向控制系統，第三代的貨車控制系統顯示了更高的隊列穩定性、更快的響應以及更短的車間距[72]. PATH 項目還對幾種用于車輛自動跟馳的油門/制動控制器進行了設計，采用經驗證的非線性縱向模型對控制器進行仿真，并在實車上進行了測試，結果表明，即使在頭車表現出不穩定的速度行為時，所提出的控制系統也具有保證車輛平穩跟馳的能力[65]. Li 等[73]對V2X 通信下的網聯車輛隊列進行控制，設計了一種基于非線性共識的縱向控制算法，利用穩定性理論分析了控制算法的收斂性，并在隊列形成、合并和分解的場景下進行現場實驗. Guo 等[74]研究了公路上貨車跟蹤控制問題，在考慮道路坡度和車輛異質型的非線性車輛模型基礎上，設計了車輛控制器，隊列穩定性得到加強.

由于車隊的隊列控制通常需要考慮多方面的因素，如車輛動力學異質性、通信時延、數據丟包、實際道路交通條件等情況，在實際應用中，很多情況未到達理論研究的效果. 關于智能網聯商用車、貨車在隊列穩定性控制方面的研究更多停留在實車實驗測試和驗證階段，如PATH、Energy ITS、GCDC等項目，還未得到大規模應用.

5 未來研究展望

目前，混合交通流穩定性研究主要集中在利用控制理論中的穩定性解析分析方法，一方面將在建模過程中推導出的混合交通流穩定性條件作為判定不同因素下穩定性值的規范標準，以此研究車隊規模、駕駛員反應時間、車輛通信時延、前車數量等對混合交通流穩定性的影響；另一方面從控制系統的角度出發，開發出混合隊列協同控制策略，以此最大限度地提高車隊系統的穩定性. 上述研究已經為混合交通流的穩定性分析奠定了良好的基礎，下面是對混合交通流穩定性分析領域的研究前景的一些思考，希望能為后續研究提供有效的幫助.

1） 實際交通現象：需要強調的是目前普遍的穩定性分析是基于一種理想的假設，即認為車隊在受到輕微擾動前是處于平衡狀態的，這樣處理使后續的數學分析更加簡單. 然而，在實際交通系統中，車輛在不同時間的駕駛狀態可能是不同的，比如會出現加速、減速、巡航、制動等駕駛動作，實際交通流難以出現穩定的狀態. 因此，為了更好地模擬實際交通現象，需要考慮車輛的實際駕駛狀態[6]，這一方面的工作仍然是非常前沿和新穎.

2） 后車跟馳行為：大部分的跟馳模型都只考慮前車對本車跟馳行為的影響，以前車的駕駛行為作為跟馳行為的控制輸入，未考慮后車的跟馳行為. 然而在實際中，后車的駕駛行為同樣受到駕駛員的關注. 此外，CAV 能夠同時獲取前后方的信息. 已有一部分研究[75-78]注意到了這點，并建立了雙向的控制模型，但更多局限在常規駕駛環境下. 因此，無論是HDV 還是CAV，其最終行駛狀態是由前方車輛、自身和后方車輛的行駛狀態共同決定的. 由于考慮前后車影響的跟馳模型更為復雜，在穩定性分析領域相關研究仍極具挑戰性.

3） CAV 的交互協同：與HDV 相比，CAV 車輛最大的優點在于具有交互協同功能，而車輛的交互協同對于車隊穩定性保持至關重要，組成一定規模的智能網聯車隊是交互協同的基本表征. 在智能網聯環境中，達到隊列穩定性和車隊規模的同步最優是關鍵的一點. 因此，利用穩定性分析進行智能網聯車車隊規模的設計值得深入探討.

4） 復雜混合交通流穩定性問題：由于車聯網技術和自動駕駛技術的不斷發展，會逐步衍生出四種不同的車輛類型[79]. CAV 即智能網聯車輛，同時具備自動性和網聯性的車輛，集合了智能汽車和車聯網的技術優勢；AV 即自動駕駛車輛，僅具備自動性的車輛，采用車載傳感器獨立于其他車輛自動駕駛；CV 即網聯人工駕駛車輛，能夠與周邊車輛和路側設備通信；HDV 即人工駕駛車輛，不具備自動性和網聯性. 現有的智能網聯混合交通流穩定性研究更多集中于兩種或三種車輛類型構成的相對簡單的混合交通流. 對于復雜混合交通流穩定性問題尚未深入探究. 根據以往的研究經驗，該類復雜混合交通流穩定性問題在研究處理上整體框架不變. 但對于每一種類型的車輛，由于其有效通信范圍、協作交互效果等方面存在明顯的差異，構建特定的跟馳模型來表征不同類型車輛的特性十分必要，該方面的研究有待進一步完善. 例如對于HDV，需要更多考慮駕駛員的屬性（如激進型和保守型）、駕駛員的記憶效應和后視效應；而對于CV，需要考慮其有效通信范圍，研究多少輛前車和后車的速度、速度差、車頭時距等信息是有效的，可能還需涉及到與前車通信失效的情況；而對于AV，構建駕駛員與車輛交互合作的擴展的跟馳模型是難點；對于CAV，其形成車隊的性質是區別于其他種類車輛的重點，目前該類研究較少. 針對這一類問題的研究尚不成熟，可以作為后續的研究方向.