矩形截面單箱雙室箱梁的畸變效應分析

王兆南 ，張元海

（蘭州交通大學土木工程學院， 甘肅 蘭州 730070）

單箱雙室箱梁在城市橋梁和公路橋梁中應用廣泛. 采用該截面形式橋梁的箱體和橋面寬度較大，在豎向荷載作用有偏心時，其畸變效應不同于單箱單室箱梁. 箱梁的畸變效應研究文獻較多，一般采用能量變分法或板元分析法都可得到一個四階控制微分方程，方程未知量為畸變角或箱梁梁肋撓度w，都能很好地揭示單箱單室箱梁的畸變效應.

張元海等[1]采用能量變分原理對單箱單室箱梁的畸變效應進行了研究，分析了雙層懸臂板對畸變的影響；徐勛等[2-3]采用廣義坐標法研究了單箱單室箱梁的畸變；王兆南等[4]采用板元分析法研究了單箱單室箱梁的畸變效應；Pezeshky 等[5]研究了寬翼緣鋼梁的畸變. 單箱單室簡支直線箱梁畸變的研究文獻較多，成果較多. 曲線箱梁因扭轉、彎曲和畸變相互耦合，畸變研究較為復雜[6-8]. 畸變的試驗研究可對畸變理論分析結果進行驗證：劉保東等[9]對連續剛構橋的扭轉和畸變進行了試驗研究；狄瑾等[10]對波形鋼腹板組合箱梁的扭轉和畸變進行了試驗研究，分析了扭轉、畸變和彎曲正應力的占比. 波形鋼腹板組合箱梁由于結構自重輕，適合大跨度橋梁的設計，其畸變也比混凝土箱梁明顯[11]，畸變研究也較深入. Li 等[12-14]研究了變截面箱梁的畸變，不同于求解常截面箱梁畸變控制微分方程常采用的初參解法，而采用紐馬克法求解變截面箱梁的畸變控制微分方程. 雙室箱梁橋的畸變不同于單室箱梁橋，藺鵬臻等[15]研究了單箱雙室箱梁對稱彎曲時的局部扭轉效應；Chidolue 等[16]研究了多室箱梁的扭轉和畸變，多數文獻在研究雙室箱梁的畸變效應時，只考慮反對稱畸變，而忽略了正對稱畸變.

單箱雙室箱梁相比單箱單室箱梁增加了一道腹板，這使得在偏心豎向荷載作用下，箱梁畸變不僅有反對稱畸變，還存在正對稱畸變. 若忽略正對稱畸變，在理論上將不完善，計算結果誤差也較大，且雙室箱梁在得出畸變翹曲慣性矩，框架橫向抗彎慣性矩時也不同于單箱單室箱梁. 由于有兩種畸變模式，因此無法采用一個微分方程來描述畸變效應，需采用兩個未知量，對應兩個微分方程才能完整描述單箱雙室箱梁的畸變效應. 本文從單箱雙室箱梁的畸變荷載分析出發，以箱梁的畸變角γd為未知量，定義正、反對稱畸變對應的畸變角，建立正、反對稱畸變的四階控制微分方程，以揭示單箱雙室箱梁的畸變效應，為單箱雙室箱梁橋的設計計算提供參考.

1 基本假定和畸變荷載

在薄壁箱梁畸變基本理論假定[1]的基礎上，結合單箱雙室箱梁在偏心荷載作用下的位移變形和實際設計需考慮的因素等，補充矩形截面單箱雙室箱梁畸變分析的假定：單箱雙室箱梁的邊腹板厚度相同，箱梁橫向變形時角點的轉角位移可忽略.

單箱雙室箱梁一般都會存在一個對稱軸y，箱梁截面尺寸如圖1 所示. 圖1 中：d、a1、a2分別為懸臂板、腹板、頂板（底板）的寬度；t1、t2、t3、t4、th分別為腹板AD、底板、腹板BC、頂板、腹板KF的厚度；e為荷載偏心距；P為單箱雙室箱梁頂板上線性分布的偏心豎向荷載 . 采用右手坐標系，O為原點. 箱梁截面各角點分別采用A、B、C、D、K、F表示.

圖1 單箱雙室箱梁截面形式Fig. 1 Cross section of single box double-cell box girder

如圖1 所示，沿梁縱向取單位長框架后，P可等效成一力矩Pe和一作用于K點的豎向力P. 力矩可分解出使箱梁發生反對稱畸變的荷載Pe/a2，豎向力P可分解出使箱梁發生正對稱畸變的荷載P/3 和2P/3，如圖2 所示. 畸變正應力可對應疊加，繼續分解的畸變荷載如式（1）所示.

圖2 正對稱和反對稱畸變荷載Fig. 2 Positive-symmetrical and antisymmetrical distortion load

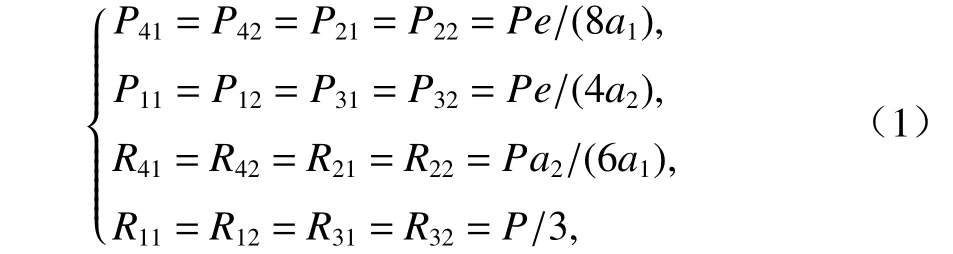
式中：P41、P42、P12、P22、P21、P11、P31和P32為反對稱畸變荷載；R41、R42、R12、R22、R21、R11、R31和R32為正對稱畸變荷載.

2 單箱雙室箱梁反對稱畸變

采用板元分析法研究單箱雙室箱梁的反對稱畸變，可得出箱梁的畸變翹曲剛度、框架橫向抗彎剛度和畸變荷載之間的關系. 箱梁發生反對稱畸變時，σdA和σdD為箱梁角點A、D的畸變正應力，令β1=σdA/σdD，畸變正應力在各板件上的分布如圖2 所示.β1可由各板件上的畸變正應力合成的對坐標軸力矩之和為0 的條件求得.

2.1 各板元面內力系分析

沿梁縱向取一微段，離散各板件，如圖3 所示.圖中：qxB、qxA、qxK為箱梁腹板對頂板的橫向約束反力；Todz為微段上腹板對頂板的縱向約束反力；Qo、Mo分別為頂板上產生的面內剪力和力矩；qxC、qxD、qxF為腹板對底板的橫向約束反力；Tudz為腹板對底板的縱向約束反力；Qu、Mu分別為底板上產生的面內剪力和力矩；qyA、qyD分別為箱梁頂板和底板對左腹板的橫向約束反力；Qc、Mc分別為左腹板面內剪力和力矩.

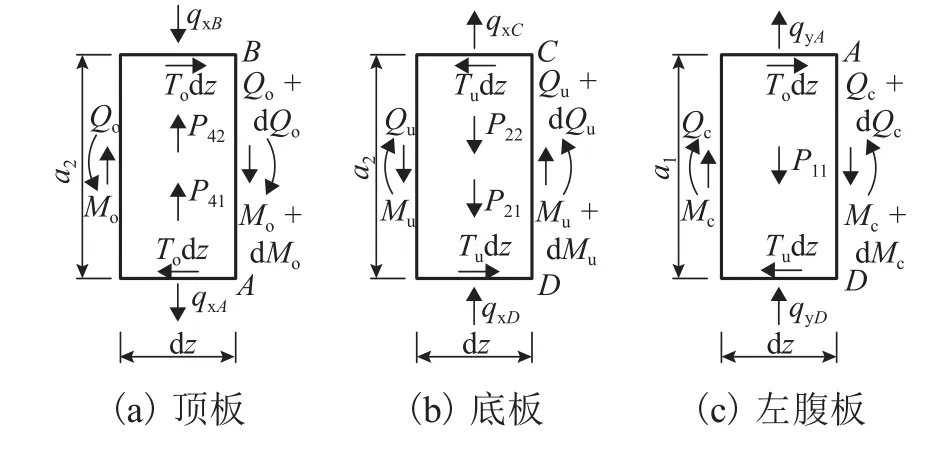
圖3 箱梁各板件的面內受力Fig. 3 In-plane force of box girder plates

由頂板、底板和腹板的面內力矩平衡，頂板和底板面內沿x軸，腹板面內沿y軸方向列取力系平衡方程. 考慮到各板件之間在畸變荷載作用下維持力系平衡狀態，略去高階微量后得出：

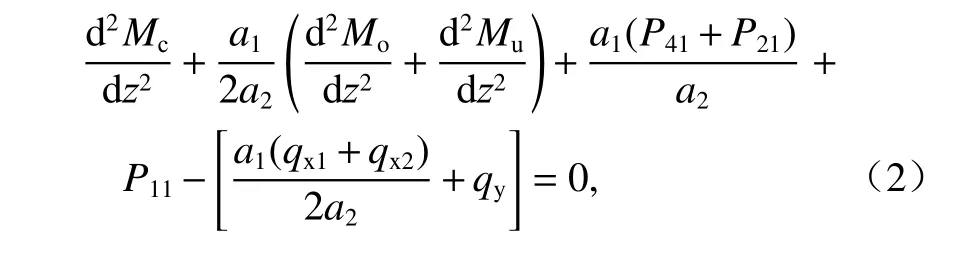
式中：qx1=qxA+qxB+qxK，qxK作用在板件AB的跨中，方向和qxA相同；qx2=qxC+qxD+qxF，qxF作用在板件CD的跨中，方向和qxC相同；qy=qyA+qyD.

箱梁在反對稱畸變時各角點的位移如圖4 所示，圖中：ΔHA、ΔHB、ΔHC、ΔHD為對應各角點水平位移；ΔVA、ΔVB、ΔVC、ΔVD為對應各角點豎向位移；α1、α2、α3為對應各板件畸變后的角度改變.

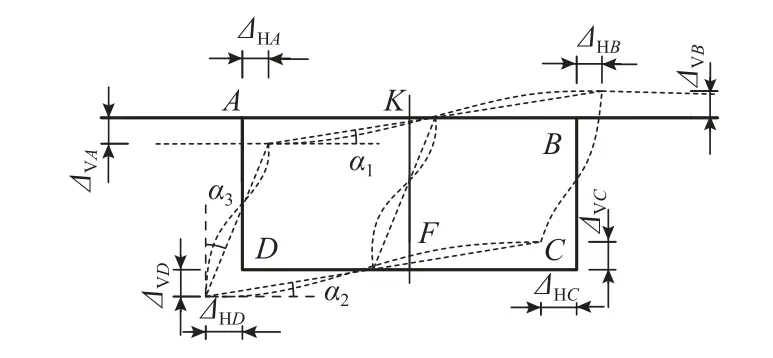
圖4 箱梁各角點的位移Fig. 4 Corner displacements of box girder

定義單箱雙室箱梁反對稱畸變的畸變角γd1為

各板件上的力矩Mo、Mu、Mc之間存在對應關系[4]. 對γd1關于z軸求二次微分后，考慮到箱梁各角點位移和面內力矩的關系[1]，得到

式中：E為材料彈性模量；J1為腹板AD（腹板BC）的面內慣性矩.

對式（4）再求二次微分后，可將式（2）化簡為

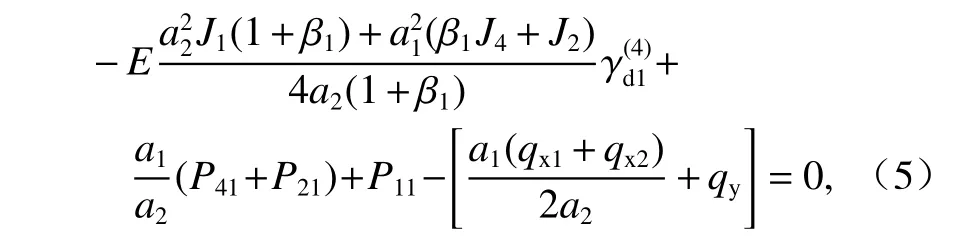
式中：Jn=tn/12 (n=1,2)，J4=t4(a2+ 2d)3/12，J2、J4分別為底板、頂板的面內慣性矩.

2.2 各板元面外力系分析

采用箱梁各板件的面外力系分析化簡式（5）中的a1(qx1+qx2)/(2a2)+qy項. 在分析過程中考慮箱梁腹板KF對框架橫向抗彎慣性矩的貢獻，單箱雙室箱梁在反對稱荷載作用下發生畸變后，離散箱梁各板件，各板件的面外受力如圖5 所示，圖中變量mAK、mAD等為各板件板端的畸變橫向彎矩.

圖5 反對稱畸變時各板件的面外受力Fig. 5 Out-of-plane force with antisymmetrical distortion

反對稱畸變時，取出板件AK和DF分析面外受力可得：qyAa2=2(mAK+mKA) ，qyDa2=2(mDF+mFD) .取出板件AD和BC分析面外受力可得：qxAa1=mAD+mDA，qxBa1=mBC+mCB，qxA=qxD，qxB=qxC. 取出板件KF分析面外受力可得：qxKa1=mKF+mFK-mKAmKB-mFC-mFD.

板件KB和FC的面外力系分析和板件AK等相同. 為得出各板件的板端畸變橫向彎矩和板端位移的關系，可采用力矩分配法進行分析，見式（6）.

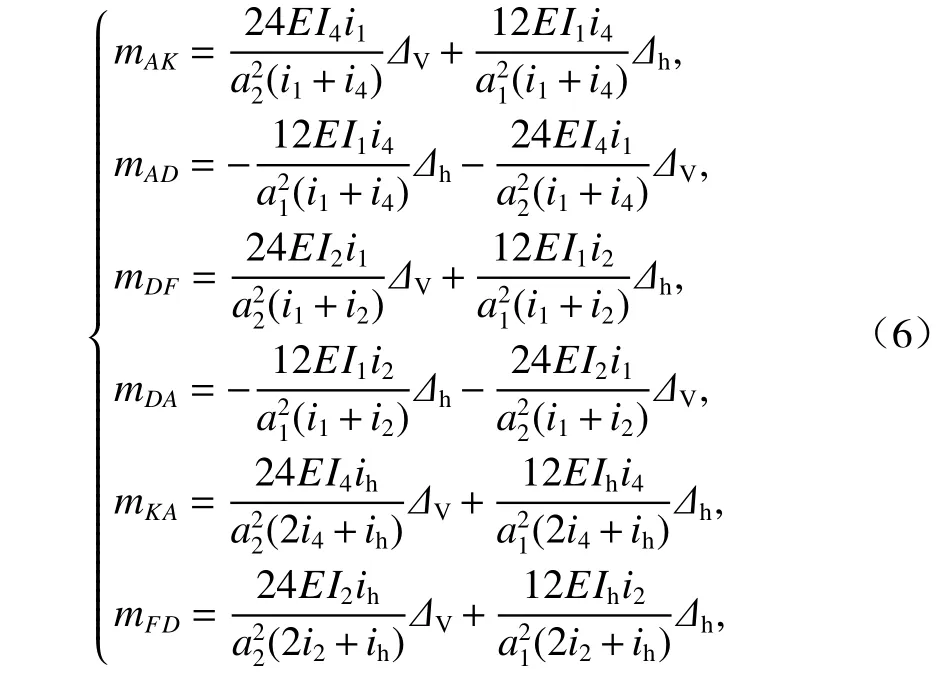
式中：i1、i2、i4、ih分別為箱梁邊腹板、底板、頂板和中腹板的線剛度；I1、I2、I4、Ih分別為箱梁邊腹板、底板、頂板和中腹板的面外慣性矩；ΔV、Δh分別為板件板端豎向位移和水平位移.

在a1(qx1+qx2)/(2a2)+qy中代入qx1、qx2、qy的表達式，結合式（6），考慮到式（3）中有ΔV=ΔVA=ΔVD，Δh=ΔHD=ΔHA，得到

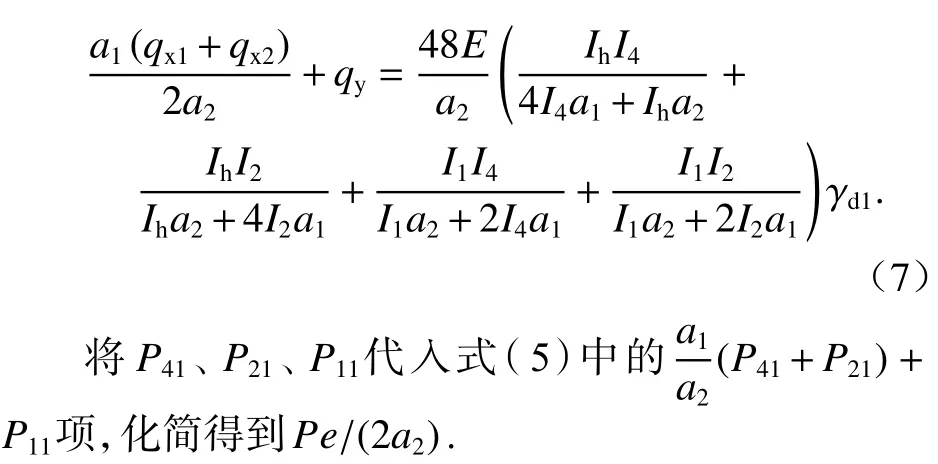
2.3 反對稱畸變控制微分方程

根據以上分析可將式（5）化簡為單箱雙室箱梁在偏心豎向荷載作用下，以反對稱畸變角γd1為未知量的四階畸變控制微分方程，如式（8）.

式中：Iωd1為單箱雙室箱梁反對稱畸變的翹曲慣性矩，單位m6，如式（9）；IR1為單箱雙室箱梁反對稱畸變的橫向抗彎慣性矩，單位m2，如式（10）.

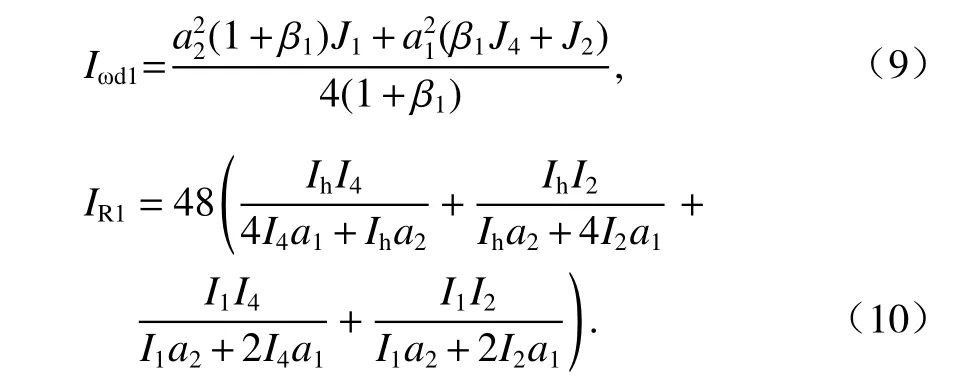
3 單箱雙室箱梁正對稱畸變

3.1 正對稱畸變時箱梁畸變翹曲慣性矩

如圖2 所示，單箱雙室箱梁在正對稱畸變荷載作用下，產生正對稱畸變翹曲變形. 按假定，畸變正應力在各板件上呈線性分布，關于y軸正對稱. 考慮到變形亦呈正對稱，頂板和底板有豎向位移，而水平位移很小幾乎可以忽略，因此可采用一半結構AKFD進行分析，如圖6 所示，圖中：h為箱梁高度. 考慮結構AKFD各角點角位移不相等的情況，當箱梁各板件厚度各不相等時，現有單箱單室箱梁畸變微分方程將不再適用，因按照假定和分析過程，其都建立在箱梁截面至少關于一個坐標軸對稱的基礎上.

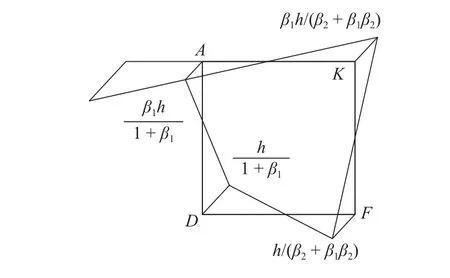
圖6 箱梁正對稱畸變扇性坐標ωdFig. 6 Positive-symmetrical distortion sector coordinates ωd

采用一個參數β1描述畸變正應力在各板件上分布的模式不再滿足箱梁各板件厚度都不同的情形. 現采用兩個參數β1和β2分別描述畸變正應力在腹板、頂板（底板）上的分布. 對各板件厚度都不同的箱梁結構，令β2=σdA/σdK（σdK為箱梁角點K的畸變正應力），認為由畸變正應力引起的面內力矩分布在頂、底板上的反彎點位置相同，但不再二等分. 在求出β1和β2后，可確定各板件厚度都不同的箱梁的畸變翹曲位移模式.

β1和β2可由各板件面內畸變正應力對x、y軸形成的力矩之和為0 的條件，且聯立式（11）、（12）求得.

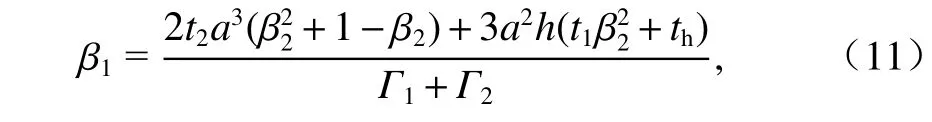
3.2 正對稱畸變時框架橫向抗彎慣性矩

結構AKFD在正對稱畸變荷載作用下發生如圖7 所示的變形. 在圖7 中：設定桿件AK和DF桿端的彎矩、轉角以逆時針為正；桿件AK和DF皆沿y軸有相同的豎向位移；MAK、MKA分別為AK桿件桿端A、K的橫向彎矩；γd2=ΔV/a，為單箱雙室發生正對稱畸變時的畸變角.

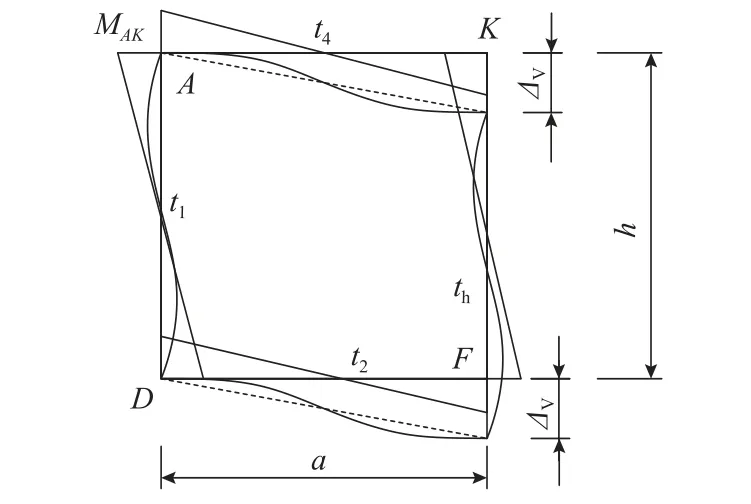
圖7 結構AKFD 的變形和橫向彎矩Fig. 7 Deformation and transverse bending moment of structure AKFD

根據分析，可忽略桿件AD和KF水平x向位移，采用桿件的轉角位移公式，可用畸變角γd2將角點D的畸變橫向彎矩表示出來，有MDF=IDγd2. 同理可得其他板件的板端彎矩：MKA=IKγd2、MAK=IAγd2、MFD=IFγd2.ID、IK、IA和IF見式（14），同時可方便地確定結構的橫向彎曲應變能.

3.3 正對稱畸變控制微分方程

沿梁軸z向取單位長框架，可得箱梁各板件的橫向彎曲應變能之和，如式（15）所示. 也可寫為，IR2為箱室各板件厚度均不相等時的框架橫向抗彎慣性矩，如式（16）.

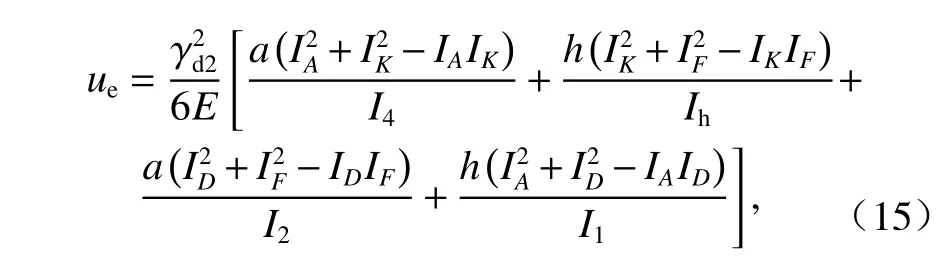
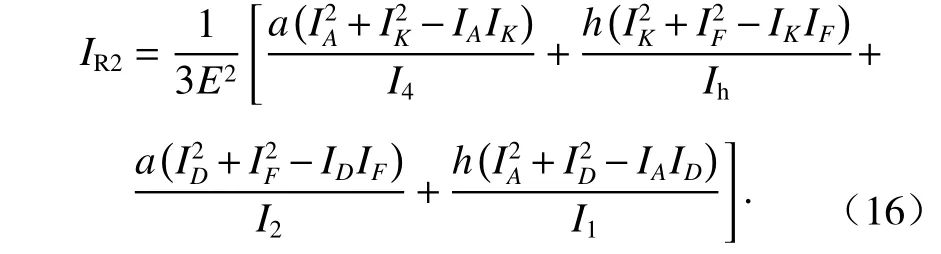
通過以上分析可得，單箱雙室箱梁發生正對稱畸變時，取一半結構得出的畸變微分方程如式（17）.IR2單位為m2，Iωd2單位為m6.

采用畸變角γd1、γd2分別描述箱梁的反對稱和正對稱畸變，得出兩個畸變微分方程，方程可采用初參數法或彈性地基梁比擬法進行求解[1,4].

4 數值算例及參數分析

在等高度矩形截面簡支箱梁上設置端橫隔板，計算跨徑L=80 m，截面如圖8 所示.E=35 GPa，泊松比μ=0. 在箱梁頂板上作用偏心豎向分布力矩1 kN · m/m，箱梁截面關于y軸對稱. 采用本文單箱雙室箱梁畸變理論進行計算分析，同時去掉中腹板按照單箱單室箱梁計算對比，得到的各畸變數值見表1，表中：Bd為畸變雙力矩；ωdA、ωdD為角點A、D的畸變扇性坐標.Bd、γd的值為彈性地基梁比擬法中單位荷載作用下的計算值，σd為實際荷載作用下的值.

表1 箱梁反對稱畸變計算值Tab. 1 Antisymmetrical distortional values

圖8 箱梁截面尺寸（單位：cm）Fig. 8 Box girder cross section （unit： cm）

單箱單室箱梁增加一道腹板成為單箱雙室箱梁后，σdA由0.521 3 kPa 變為0.209 4 kPa，應力減小率為：（0.521 3-0.209 4）/ 0.521 3 × 100%=59.83%，σdD的減小率也為59.83%. 因單室和雙室箱梁反對稱畸變的假定相同，角點應力比β1數值不變，各角點的畸變扇性坐標數值不變. 由于中腹板增強了截面的橫向抗彎剛度，箱梁的框架橫向抗彎慣性矩從單室的0.004 0 增大到雙室的0.009 6.

算例箱梁正對稱畸變計算值如表2 所列. 單箱雙室箱梁角點A的正對稱畸變正應力為反對稱畸變值的28.08%，角點D為26.76%. 若取的一半結構按照傳統的單箱單室箱梁畸變方法計算角點畸變正應力，角點D的值為單箱雙室箱梁反對稱畸變值的1.97 倍，為按照本文正對稱畸變計算值的7.37 倍.

表2 箱梁正對稱畸變計算值Tab. 2 Positive-symmetrical distortional values

最終單箱雙室箱梁角點A、D的畸變正應力為箱梁正、反對稱畸變計算結果的疊加，如表3. 并與有限元結果進行對比，有限元計算采用Shell-63 單元建模分析. 從角點A、D的畸變正應力誤差來看，本文方法解析解和有限元解最大誤差的絕對值不超過8.71%，角點A的畸變正應力誤差僅為1.73%，有限元解和解析解吻合良好.

本文方法得到的雙室箱梁和按單箱單室箱梁計算的角點A、D的應力值如表3 和表1 所示. 考慮箱梁的正對稱畸變后，箱梁由單箱單室變成單箱雙室時，角點A畸變正應力的減小率由59.83%變為48.52%，角點D畸變正應力的減小率由59.83%變為49.09%，如忽略正對稱畸變的影響，畸變效應和有限元結果的誤差將會增大. 雙室箱梁的畸變正應力比單室箱梁的要小. 當箱梁橫向寬度較大時，增設中腹板可有效減小箱梁的畸變效應.

表3 箱梁角點畸變正應力Tab. 3 Corner distortion normal stress of box girder

為更好地比較兩種截面形式箱梁的畸變效應差別. 單箱單室和單箱雙室簡支箱梁跨中截面的畸變角、角點畸變正應力的對比如圖9、10 所示. 由圖9可知：單箱雙室箱梁的反對稱畸變角沿梁長的分布在畸變角數值的絕對值上小于單箱單室箱梁；中腹板對箱梁畸變的削弱非常明顯，跨中截面畸變角迅速變小；在梁端一定區域內，雙室箱梁的畸變角變化比單室的平穩，雙室箱梁在此區域的反向變形小于單室箱梁，畸變角較早地衰減趨向于0，偏心豎向荷載引起的畸變較單箱單室箱梁的小，較好地反映了增加的箱室腹板對畸變的限制作用，與增加梁跨內橫隔板效果相同.

圖9 畸變角沿梁長變化Fig. 9 Distortional angle changes of box girder

由圖10 可知：對箱梁畸變正應力沿梁長的分布進行分析，單室箱梁和雙室箱梁角點A的畸變正應力沿梁長的分布有著明顯的區別；雙室箱梁角點A畸變正應力在數值的絕對值上明顯小于單室箱梁，在跨中截面有最大值；雙室箱梁角點A的畸變正應力向梁端衰減很快，而單室箱梁則衰減較慢. 從以上分析可以看出，雙室箱梁畸變角、畸變正應力計算值都小于單室箱梁，中腹板對箱梁畸變的限制是非常明顯的.

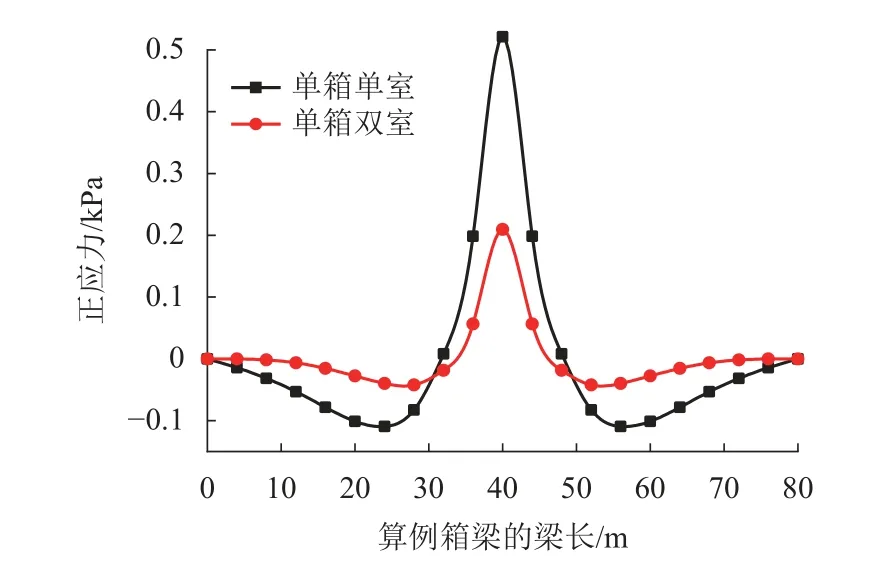
圖10 角點A 畸變正應力沿梁長變化Fig. 10 Changes of distortional normal stress of point A

取中腹板厚度為0.10、0.15、0.20、0.25、0.30、0.35、0.40、0.45、0.50 m，其他條件皆不變，分析箱梁跨中截面反對稱畸變角隨中腹板厚度變化的規律. 中腹板厚度變化時，雙室箱梁反對稱畸變的畸變角沿梁長的變化情況如圖11 所示. 選取中腹板厚度為0.10、0.30、0.50 m 的數據列出，0.10 m 厚的板為薄板，0.30 m厚的板為薄板和厚板的界限，0.50 m 厚的板為厚板.

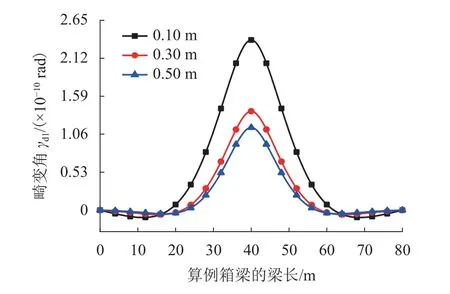
圖11 中腹板厚度對箱梁畸變角的影響Fig. 11 Influence of mid-web thickness on distortional angle of box girder

從圖11 可以看出：不同中腹板厚度的雙室箱梁反對稱畸變角沿梁長的變化趨勢在箱梁跨中截面區域內基本相同，在箱梁梁端附近變化趨勢有所不同；隨著中腹板厚度的增加，在梁端附近，畸變角的變化逐漸平穩，雙室箱梁在梁端附近畸變翹曲的程度較小；中腹板厚度為0.10 m 的雙室箱梁畸變角在梁端附近的反向變形比0.50 m 板厚的要突出，薄壁箱梁的畸變翹曲程度比厚壁的要明顯；隨著板厚的增加，雙室箱梁的畸變逐漸減小，僅在跨中一定長度范圍內畸變較為明顯，梁兩端逐漸減弱，梁端變形程度較小的區域逐漸向跨內延伸；0.50 m 板厚的雙室箱梁梁端畸變較小的區域較0.10 m 板厚的區域要長.

5 結 論

1） 在偏心豎向荷載作用下，單箱雙室箱梁不僅存在反對稱畸變，還存在正對稱畸變. 正對稱畸變正應力較小，本文算例中，最大只占到反對稱畸變正應力的28.08%.

2） 考慮了正對稱畸變效應后，雙室箱梁的畸變分析在理論上將更加完善. 通過數值計算顯示，畸變正應力解析解和有限元解的誤差減小，誤差絕對值最大為8.71%，相互吻合更好.

3） 當箱體較寬的單箱單室箱梁增設中間腹板成為單箱雙室箱梁后，箱梁角點處的畸變正應力可減少到單室箱梁的49.09%. 為減小寬箱梁在偏心豎向荷載作用下的畸變，設置中腹板效果明顯.

4） 單箱雙室簡支箱梁的畸變比單箱單室簡支箱梁的要小，變形主要在跨中一定的區域內，梁端附近的區域反向變形不如單箱單室的明顯. 中腹板厚度的變化可使雙室箱梁的畸變發生較明顯的改變，厚度較小時畸變較為明顯，厚度增大時畸變逐漸減弱.

5） 采用兩個參數β1、β2描述正對稱畸變時，單箱雙室箱梁各板件上的畸變正應力分布比一個參數的合理. 采用一個參數的箱梁畸變理論計算的正對稱畸變效應，箱梁角點畸變正應力最大可為本文方法的7.37 倍.