數(shù)隨形變變則歸一

文／謝曉華

華羅庚說(shuō)：“數(shù)缺形時(shí)少直觀，形缺數(shù)時(shí)難入微。”數(shù)與形的結(jié)合可以幫助我們直觀地解決很多數(shù)學(xué)問(wèn)題。不僅如此，在幾何問(wèn)題中，圖形中的“位置關(guān)系”決定著“數(shù)量關(guān)系”。在圓這一章中，點(diǎn)、線、角、弧與圓位置關(guān)系的情況比較多，我們稍不注意，就會(huì)導(dǎo)致漏解、錯(cuò)解。

類型一 點(diǎn)與圓的位置關(guān)系

例1點(diǎn)M是非⊙O上的一點(diǎn)，若點(diǎn)M到⊙O上的點(diǎn)的最小距離是4，最大距離是8，則⊙O的半徑是____。

【錯(cuò)解】6。

【錯(cuò)因分析】點(diǎn)和圓的位置關(guān)系有三種：點(diǎn)在圓內(nèi)、圓外、圓上。此處忽略了點(diǎn)在圓外這種位置關(guān)系，導(dǎo)致漏解。

【正解】本題有如下兩種情況：

如圖1，當(dāng)點(diǎn)M在⊙O內(nèi)，連接OM，過(guò)點(diǎn)M作直徑AB，則AM=8，BM=4。

圖1

∵⊙O的直徑AB=AM+BM=8+4=12，

如圖2，當(dāng)點(diǎn)M在⊙O外時(shí)，同理可得⊙O的半徑=

圖2

綜上，⊙O的半徑是6或2。

【總結(jié)】處理點(diǎn)與圓的相關(guān)問(wèn)題時(shí)，從“位置關(guān)系”來(lái)看有三種情況：點(diǎn)在圓內(nèi)、圓外、圓上；從“數(shù)量關(guān)系”來(lái)看，點(diǎn)在圓內(nèi)、圓外這兩種情況對(duì)應(yīng)圓的半徑分別為：點(diǎn)到圓上距離的最大值與最小值之和的一半、點(diǎn)到圓上距離的最大值與最小值之差的一半。

類型二 圓心與圓內(nèi)兩條平行弦的位置關(guān)系

例2⊙O中兩條平行的弦長(zhǎng)分別為AB=6和CD=8，圓的半徑為5，則兩條平行弦AB和CD之間的距離為_(kāi)___。

【錯(cuò)解】1。

【錯(cuò)因分析】圓心與圓中的兩條平行弦有兩種位置關(guān)系：圓心在兩條平行線之間，圓心在兩條平行線外。此處忽略了圓心在兩條平行線之間的情況，導(dǎo)致漏解。

【正解】本題有如下兩種情況：

如圖3，當(dāng)圓心在兩條平行線之間時(shí)，過(guò)點(diǎn)O作OM⊥AB交AB于點(diǎn)M，延長(zhǎng)MO交CD于點(diǎn)N，連接OB、OD。

圖3

∵OM⊥AB，

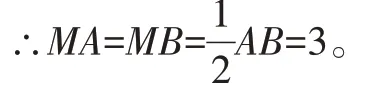
在Rt△BOM中，∠BMO=90°，

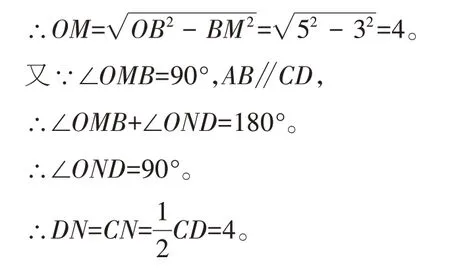
在Rt△DON中，∠OND=90°，

如圖4，當(dāng)圓心在兩條平行弦AB和CD外時(shí)，同理可得兩條平行弦間的距離為1。

圖4

綜上，兩條平行弦AB和CD之間的距離為7或1。

【總結(jié)】在圓中，圓心與圓內(nèi)一組平行弦的關(guān)系，從“位置關(guān)系”來(lái)看有兩種情況：圓心在兩條平行線之間，圓心在兩條平行線外；從“數(shù)量關(guān)系”來(lái)看，平行弦之間的距離等于圓心到兩條弦之間的距離和或差。

類型三 圓心與圓周角的位置關(guān)系

例3⊙O的半徑為2，弦AB=2，AC=2，則∠BAC的度數(shù)為_(kāi)__。

【錯(cuò)解】15°。

【錯(cuò)因分析】圓心與圓周角的位置關(guān)系有兩種：圓心在圓周角內(nèi)，圓心在圓周角外。此處忽略了圓心在圓周角內(nèi)的情況，導(dǎo)致了漏解。

【正解】本題有如下兩種情況：

如圖5，當(dāng)圓心在圓周角∠CAB內(nèi)部時(shí)，過(guò)點(diǎn)O作OM⊥AB、ON⊥AC，分別交AB、AC于點(diǎn)M、N，連接OA。

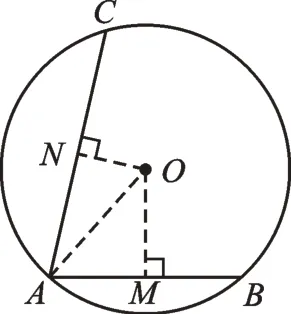
圖5

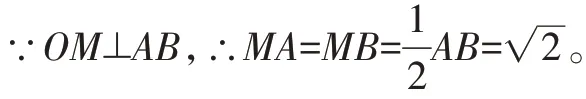
在Rt△AOM中，∠AMO=90°，

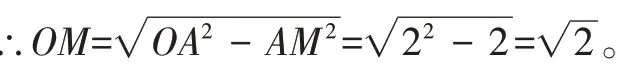
∴△AOM為等腰直角三角形。

∴∠AOM=∠OAB=45°。

(3)新疆巴里坤膨潤(rùn)土礦富Al2O3、Fe2O3、Na2O、TiO2，貧Si2O、K2O、MgO。巴里坤膨潤(rùn)土礦床的母質(zhì)為基性非富硅物質(zhì)。Na2O的含量遠(yuǎn)遠(yuǎn)大于CaO，且ENa2+/CEC為83.5%，為鈉基膨潤(rùn)土。

同理，在Rt△AON中，NA=3，OA=2，ON=1，∴∠OAN=30°。

∴∠BAC=∠OAB+∠OAC=45°+30°=75°。

如圖6，當(dāng)圓心在圓周角∠CAB外部時(shí)，同理可得∠BAC=∠OAB-∠OAC=45°-30°=15°。

圖6

綜上，∠BAC=75°或15°。

【總結(jié)】在圓中，對(duì)于圓心與圓周角，從“位置關(guān)系”來(lái)看有兩種：圓心在圓周角內(nèi)，圓心在圓周角外；從“數(shù)量關(guān)系”來(lái)看，∠BAC的度數(shù)分別為圓周角頂點(diǎn)和圓心的連線與圓周角的兩邊構(gòu)成的兩個(gè)角的和與差。

類型四 動(dòng)點(diǎn)與弧的位置關(guān)系

例4點(diǎn)P為⊙O外一點(diǎn)，PA、PB分別與⊙O相切于A、B兩點(diǎn)，點(diǎn)C為⊙O上與A、B不重合的點(diǎn)，若∠P=30°，則∠C的度數(shù)為_(kāi)___。

【錯(cuò)因分析】點(diǎn)在圓上時(shí)，點(diǎn)與圓弧有兩種位置關(guān)系：點(diǎn)在優(yōu)弧上，點(diǎn)在劣弧上。此處忽略了點(diǎn)在劣弧上的情況，導(dǎo)致漏解。

【正解】本題有如下兩種情況：

如圖7，當(dāng)點(diǎn)C在優(yōu)弧上時(shí)，連接OA、OB。

圖7

∵PA與⊙O相切于A點(diǎn)，OA是⊙O的半徑，∴∠OAP=90°。

同理，∠OBP=90°。

在四邊形AOBP中，∠OAP+∠P+∠OBP+∠AOB=360°。

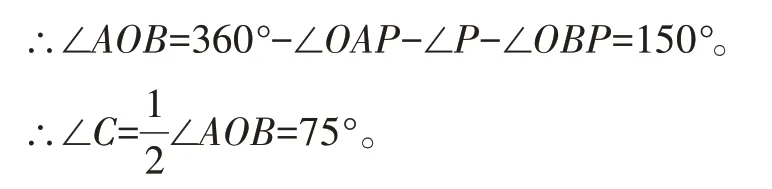
如圖8，當(dāng)點(diǎn)C在劣弧上時(shí)。

圖8

∵四邊形ACBC′是⊙O的內(nèi)接四邊形，

∴∠C+∠C′=180°。∴∠C′=105°。

綜上，∠C=75°或105°。

【總結(jié)】在圓中，對(duì)于點(diǎn)與圓弧，從“位置關(guān)系”來(lái)看有兩種情況：點(diǎn)在優(yōu)弧上，點(diǎn)在劣弧上；從“數(shù)量關(guān)系”來(lái)看，這兩種情況下的兩個(gè)角互為補(bǔ)角。同學(xué)們可以利用切線、圓周角定理、圓內(nèi)接四邊形求解。

“數(shù)”與“形”是數(shù)學(xué)知識(shí)的核心構(gòu)成要素，尤其是在幾何的學(xué)習(xí)過(guò)程中，數(shù)量關(guān)系和位置關(guān)系是數(shù)與形關(guān)系的直接體現(xiàn)。在圓這一章的學(xué)習(xí)過(guò)程中，我們要考慮點(diǎn)、線、角、弧在圖形中的不同位置。位置關(guān)系不同，數(shù)量關(guān)系也會(huì)發(fā)生變化，更深入地分析可以發(fā)現(xiàn)：不同位置關(guān)系下對(duì)應(yīng)的數(shù)量關(guān)系之間也存在著對(duì)應(yīng)關(guān)系。也正是位置的不確定，我們才需要分類討論出不同的數(shù)量關(guān)系。