抗蛇行減振器節(jié)點(diǎn)剛度對(duì)列車(chē)轉(zhuǎn)向架橫向振動(dòng)特性的影響研究

陳國(guó)泰，盧 婧，程 剛

(1.中國(guó)鐵路西安局集團(tuán)有限公司 西安客車(chē)車(chē)輛段，陜西 西安 710024；2.中國(guó)石油天然氣股份有限公司 長(zhǎng)慶油田分公司，陜西 西安 710000)

采用抗蛇行減振器是抑制轉(zhuǎn)向架蛇行失穩(wěn)的重要手段，抗蛇行減振器縱向安裝于車(chē)體與轉(zhuǎn)向架之間，通過(guò)提供二系回轉(zhuǎn)力矩來(lái)提高鐵道客車(chē)系統(tǒng)的穩(wěn)定性，因此成為鐵道客車(chē)重要的懸掛元件[1-2]。過(guò)去對(duì)于車(chē)輛系統(tǒng)的建模，較少考慮減振器兩端橡膠節(jié)點(diǎn)的彈性，在模型中多作為剛性來(lái)處理。但在實(shí)際的車(chē)輛系統(tǒng)中減振器兩端都加有橡膠彈性節(jié)點(diǎn)，其目的是一方面提高系統(tǒng)的隔振和降噪能力；另一方面是避免減振器兩端相連部件如輪對(duì)、轉(zhuǎn)向架和車(chē)體其他方向的振動(dòng)影響減振器正常工作，從而延長(zhǎng)減振器的使用壽命[3-6]。抗蛇行減振器兩端與轉(zhuǎn)向架、車(chē)體的連接接頭有5種，分別為橡膠墊式、球形橋式、球形銷(xiāo)式、無(wú)外套橋式和無(wú)外套銷(xiāo)式，具體用哪種形式需要根據(jù)其安裝位置和與之連接體的結(jié)構(gòu)決定。減振器節(jié)點(diǎn)剛度在連接體的x、y和z方向上均有分布，通常對(duì)其進(jìn)行簡(jiǎn)化，只考慮其安裝方向的安裝剛度，忽略其他方向的剛度。

抗蛇行減振器是車(chē)輛懸掛系統(tǒng)中非常重要的懸掛元件，建立合理的模型并與車(chē)輛模型結(jié)合起來(lái)研究轉(zhuǎn)向架橫向振動(dòng)特性是非常有必要的。本文將建立17自由度列車(chē)橫向振動(dòng)系統(tǒng)模型，并且將抗蛇行減振器Maxwell模型引入其中，得到改進(jìn)后的列車(chē)橫向振動(dòng)系統(tǒng)模型，應(yīng)用隨機(jī)振動(dòng)理論來(lái)分析研究抗蛇行減振器節(jié)點(diǎn)剛度隨著頻率的變化對(duì)列車(chē)轉(zhuǎn)向架橫向振動(dòng)特性的影響，以期為抗蛇行減振器節(jié)點(diǎn)的結(jié)構(gòu)設(shè)計(jì)和相關(guān)振動(dòng)參數(shù)的優(yōu)化提供參考和依據(jù)。

1 抗蛇行減振器橡膠節(jié)點(diǎn)彈性懸掛的數(shù)學(xué)模型

考慮車(chē)體和轉(zhuǎn)向架的結(jié)構(gòu)，用數(shù)學(xué)模型展示減振器兩端橡膠節(jié)點(diǎn)彈性懸掛。圖1為質(zhì)量-彈簧-阻尼系統(tǒng)，其中k和k0為懸掛系統(tǒng)彈簧剛度，c和kr分別為減振器阻尼和橡膠節(jié)點(diǎn)剛度，m1為車(chē)體，m2為構(gòu)架，z1和z2分別為m1和m2的位移，z3和z4是抗蛇行減振器2個(gè)橡膠節(jié)點(diǎn)連接處的位移，u為外界輸入不平順激勵(lì)。

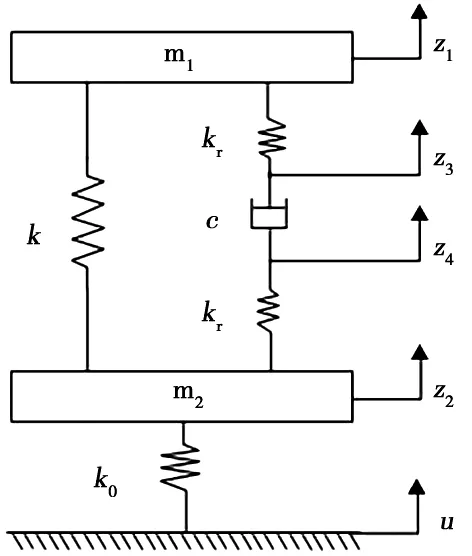
圖1 質(zhì)量-彈簧-阻尼系統(tǒng)

由動(dòng)力學(xué)定律，可得出圖1所示系統(tǒng)的運(yùn)動(dòng)微分方程組：

(1)

令Δz=z3-z4，變換關(guān)系為：

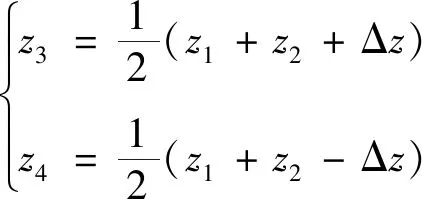
(2)

代入式(1)后，得：

對(duì)于列車(chē)橫向振動(dòng)系統(tǒng)，一系和二系懸掛均安裝有減振器，可運(yùn)用該數(shù)學(xué)模型的方法進(jìn)行分析。

2 列車(chē)橫向振動(dòng)系統(tǒng)的模型建立

基于對(duì)力學(xué)模型簡(jiǎn)化的基本原則，簡(jiǎn)化后的列車(chē)橫向振動(dòng)系統(tǒng)計(jì)算分析簡(jiǎn)圖如圖2所示。仿真條件假設(shè)車(chē)體與轉(zhuǎn)向架當(dāng)作剛體，輪軌為剛性接觸，忽略零部件的柔性屬性；車(chē)輛行駛過(guò)程中輪軌一直是相接觸的；抗蛇行減振器視為非線性元件，其他懸掛元件是線性的；車(chē)體與轉(zhuǎn)向架的位置在笛卡爾坐標(biāo)系中縱向和垂直平面內(nèi)與其質(zhì)心對(duì)稱；仿真過(guò)程中車(chē)輛是勻速直線行駛的，主要考慮車(chē)輛各部分在橫向平面中的振動(dòng)，忽略垂向的弱耦合作用。

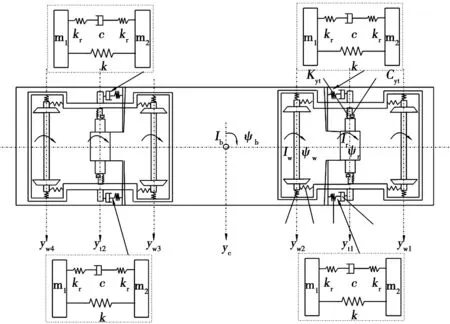
Kyt.二系懸掛橫向剛度；Cyt.二系懸掛橫向阻尼；yw1、yw2.、yw3、yw4.1位、2位、3位、4位輪對(duì)橫向運(yùn)動(dòng)位移；yt1、yt2.1位、2位構(gòu)架橫向運(yùn)動(dòng)位移；yc.車(chē)體橫向運(yùn)動(dòng)位移；Ib、Iw、Ir.車(chē)體、輪對(duì)、構(gòu)架的側(cè)滾角位移；Ψb、Ψw、Ψr.車(chē)體搖頭角位移。

整車(chē)總共17個(gè)自由度，轉(zhuǎn)向架二系懸掛2個(gè)抗蛇行減振器，計(jì)算轉(zhuǎn)向架搖頭作用力時(shí)，其等同于1個(gè)抗蛇行減振器作用力的2倍，在推導(dǎo)方程時(shí)只需增加1個(gè)抗蛇行減振器的相對(duì)位移量。橫向減振器做同樣處理，橫向振動(dòng)中考慮4個(gè)相對(duì)位移量，這樣即可得到向量形式的微分方程組：

(4)

式中：y——系統(tǒng)的自由度向量；

y1——減振器相對(duì)位移向量；

Fc，F(xiàn)g,f(t)——整車(chē)門(mén)自由度向量矩陣；

M，C，K——分別為質(zhì)量矩陣、阻尼矩陣、剛度矩陣。

3 多點(diǎn)完全相干平穩(wěn)激勵(lì)的虛擬激勵(lì)法

與傳統(tǒng)的車(chē)輛隨機(jī)振動(dòng)隨機(jī)響應(yīng)的分析方法相比較，虛擬激勵(lì)法具有計(jì)算簡(jiǎn)單、計(jì)算量小的特點(diǎn)。而虛擬激勵(lì)法同樣在軌道車(chē)輛振動(dòng)中也得到了相關(guān)應(yīng)用，車(chē)輛運(yùn)行中輪對(duì)接觸鋼軌產(chǎn)生的作用力被認(rèn)為只是時(shí)間前后的差異，輪對(duì)所受力的大小方向是相同的，這樣可以高效準(zhǔn)確地解決車(chē)輛橫向振動(dòng)問(wèn)題。

針對(duì)多輪對(duì)軌道車(chē)輛，應(yīng)用多點(diǎn)完全相干平穩(wěn)激勵(lì)的虛擬激勵(lì)法。設(shè)4條輪對(duì)異相位平穩(wěn)隨機(jī)激勵(lì)為f(t)，得到：

(5)

式中：ai——輪軌接觸點(diǎn)處激勵(lì)強(qiáng)弱的系數(shù)，且4條輪對(duì)受到的激勵(lì)強(qiáng)度相同，令ai=1；

F(t)——時(shí)間歷程函數(shù)；

ti——系統(tǒng)受力前后時(shí)間差常數(shù)，i=1，2，3，4。

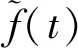
(6)

式中：i——1～4位輪對(duì)；

ω——圓頻率；

SFF(ω)——自功率譜密度函數(shù)。

軌道車(chē)輛的動(dòng)力學(xué)方程具有的一般形式：

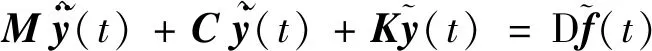
(7)

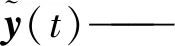
將式(6)代入式(7)可得：

(8)

得到響應(yīng)的功率譜Syy為：

(9)

通過(guò)ω和f的轉(zhuǎn)化可得到加速度功率譜密度響應(yīng)，以矩陣形式表示為：

(10)

系統(tǒng)振動(dòng)位移的功率譜密度矩陣可表示為：

(11)

式中：*——復(fù)共軛，取ω=2πf。

通過(guò)轉(zhuǎn)化得到系統(tǒng)加速度功率譜密度矩陣：

(12)

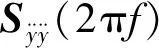
4 數(shù)值分析

4.1 車(chē)輛與軌道條件

以某型軌道客車(chē)為例，其橫向模型主要參數(shù)見(jiàn)表1，以美國(guó)Ⅵ級(jí)軌道方向不平順作為橫向振動(dòng)模型頻域研究的仿真激勵(lì)，其功率譜密度曲線如圖3所示。

表1 某型軌道車(chē)輛橫向模型主要參數(shù)

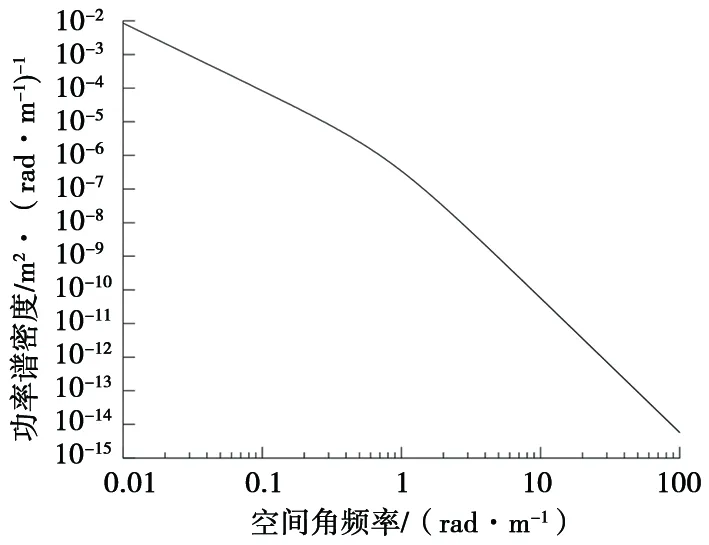
圖3 美國(guó)Ⅵ級(jí)軌道方向不平順的功率譜密度曲線

4.2 仿真計(jì)算與結(jié)果分析

設(shè)定車(chē)輛直線行駛速度分別為60 km/h、120km/h、160 km/h，含Maxwell抗蛇行減振器模型的17自由度橫向振動(dòng)系統(tǒng)改進(jìn)模型的參數(shù)值保持不變，對(duì)其轉(zhuǎn)向架在頻域內(nèi)的振動(dòng)特性進(jìn)行仿真研究。

圖4為客車(chē)以不同速度運(yùn)行時(shí)，前后轉(zhuǎn)向架的橫移、側(cè)滾、搖頭位移功率譜密度曲線。從圖4中可以看出，在不同運(yùn)行速度下，前后轉(zhuǎn)向架橫移、側(cè)滾、搖頭位移功率譜密度隨速度的變化趨勢(shì)大致相似，但其對(duì)應(yīng)的功率譜密度有所不同。隨著客車(chē)運(yùn)行速度的變化，車(chē)速與前后轉(zhuǎn)向架的位移功率譜密度呈正相關(guān)。由此可見(jiàn)：客車(chē)運(yùn)行速度是影響轉(zhuǎn)向架橫向振動(dòng)的一個(gè)重要因素。從圖4中還可以看出，前后轉(zhuǎn)向架位移功率譜密度峰值均在2～10 Hz內(nèi)出現(xiàn)，因此影響前后轉(zhuǎn)向架橫移、側(cè)滾、搖頭振動(dòng)的頻率范圍較低。

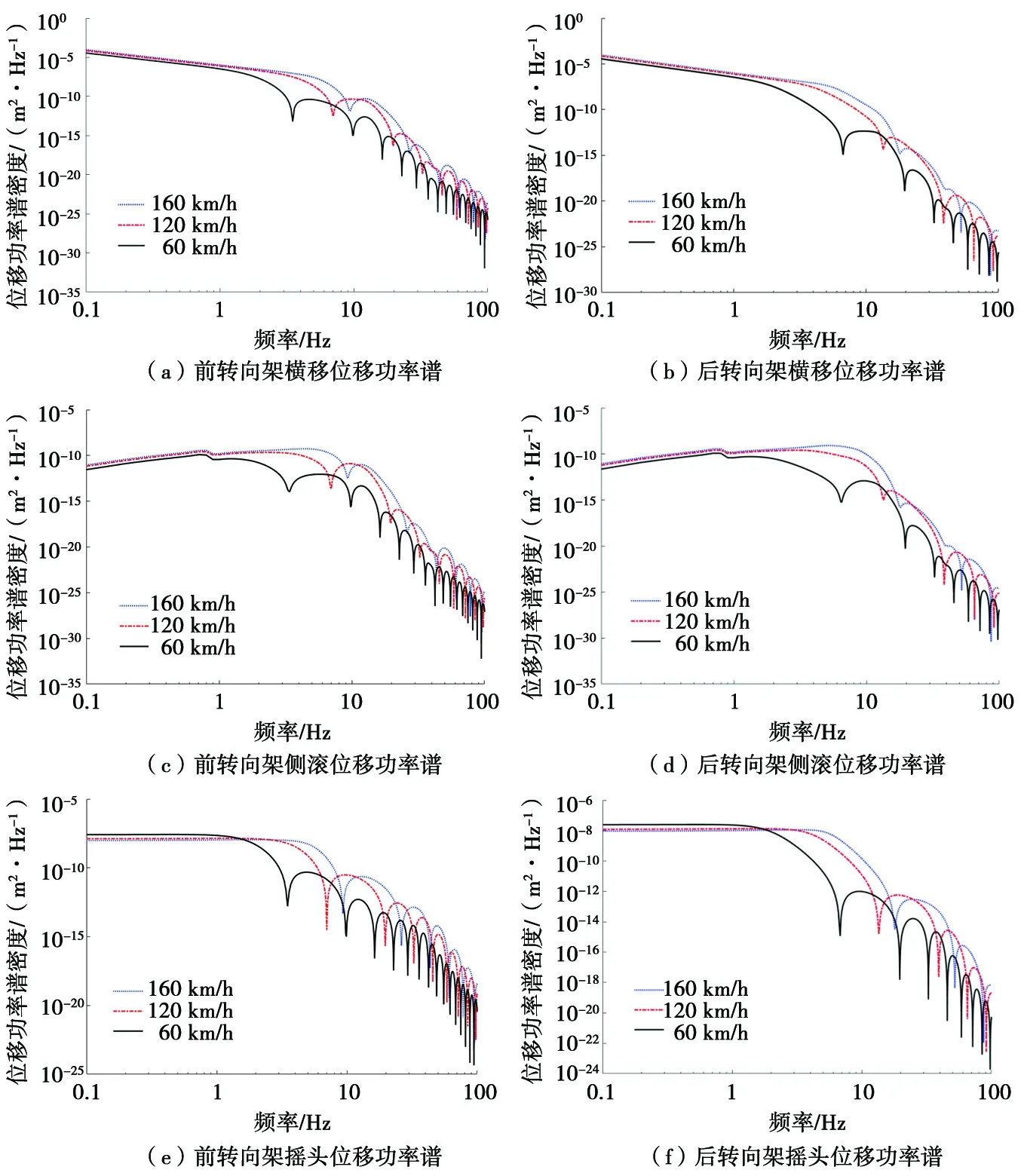
圖4 不同車(chē)速下前后轉(zhuǎn)向架位移功率譜密度曲線

保持車(chē)輛振動(dòng)系統(tǒng)模型不變，車(chē)輛運(yùn)行速度為120 km/h時(shí)，抗蛇行減振器節(jié)點(diǎn)剛度原參數(shù)為35 MN/m，其他參數(shù)均為固定值，分別取原值附近2個(gè)剛度值17.5 MN/m、70 MN/m，通過(guò)對(duì)抗蛇行減振器節(jié)點(diǎn)剛度值下的車(chē)輛振動(dòng)系統(tǒng)進(jìn)行仿真，得到前后轉(zhuǎn)向架橫向振動(dòng)的頻域響應(yīng)。

圖5為車(chē)輛在不同抗蛇行減振器節(jié)點(diǎn)剛度下的前后轉(zhuǎn)向架橫移、側(cè)滾、搖頭加速度功率譜密度曲線。由圖5可以看出，在不同抗蛇行減振器節(jié)點(diǎn)剛度下，前后轉(zhuǎn)向架橫移、側(cè)滾加速度功率譜密度隨節(jié)點(diǎn)剛度的變化差異較大，其對(duì)應(yīng)的功率譜也有所不同。在0～40 Hz內(nèi)，抗蛇行減振器節(jié)點(diǎn)剛度值越大，前后轉(zhuǎn)向架橫移和側(cè)滾加速度功率譜密度越小，與節(jié)點(diǎn)剛度呈負(fù)相關(guān)。前后轉(zhuǎn)向架搖頭加速度功率譜密度在0～5.5 Hz內(nèi)隨著抗蛇行減振器節(jié)點(diǎn)剛度增大而增大。由此可見(jiàn)，在不同頻率范圍內(nèi)，抗蛇行減振器節(jié)點(diǎn)剛度的取值對(duì)轉(zhuǎn)向架橫移、側(cè)滾、搖頭加速度功率譜密度影響顯著。

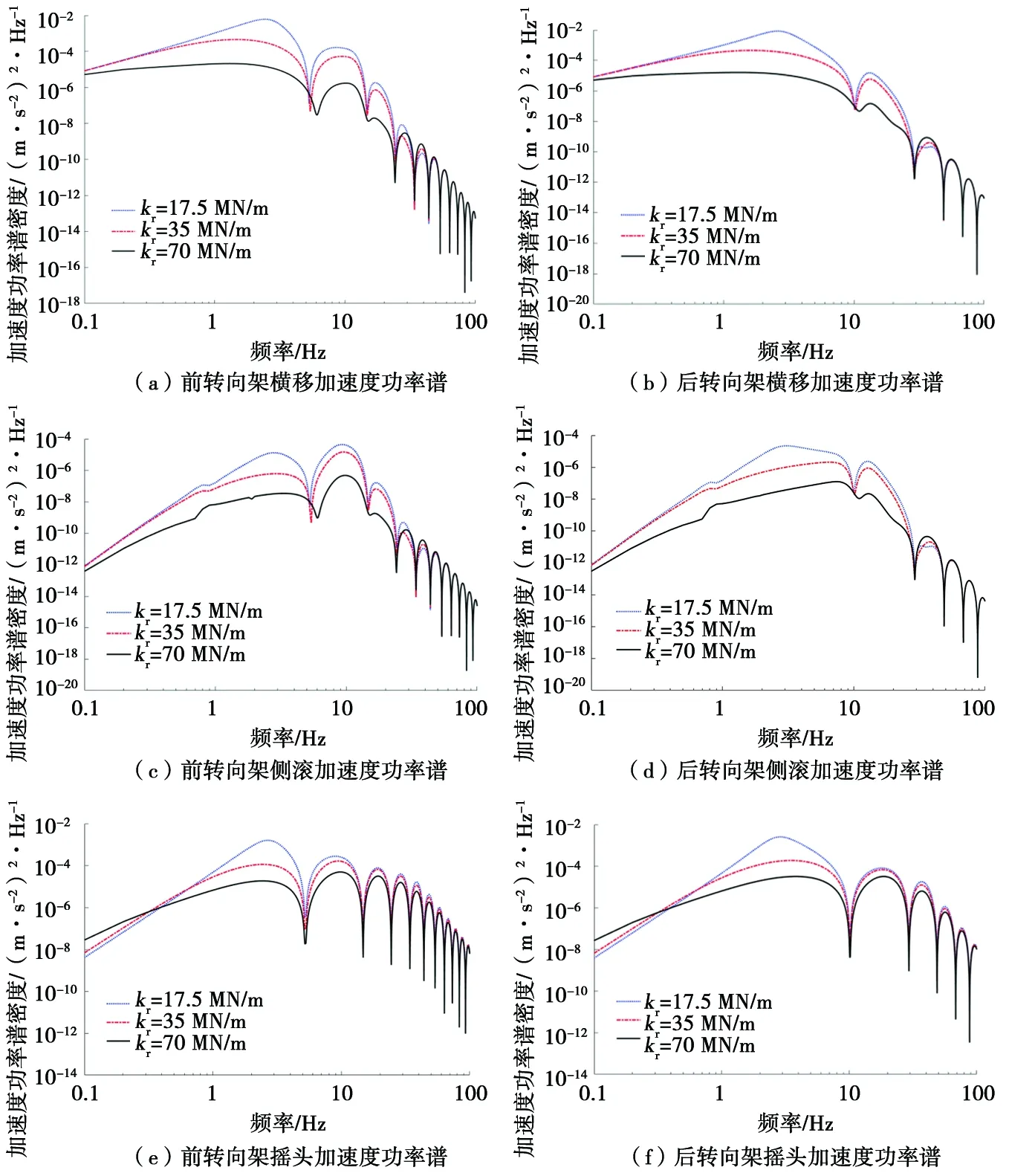
圖5 不同節(jié)點(diǎn)剛度下前后轉(zhuǎn)向架加速度功率譜密度曲線

5 結(jié)論

列車(chē)運(yùn)行速度是影響軌道車(chē)輛橫向振動(dòng)系統(tǒng)轉(zhuǎn)向架橫向加速度功率譜的一個(gè)重要因素。隨著運(yùn)行速度的提高，前后轉(zhuǎn)向架橫移、側(cè)滾、搖頭位移功率譜密度和振動(dòng)主頻均增大，而且影響前后轉(zhuǎn)向架橫移、側(cè)滾、搖頭振動(dòng)的頻率范圍較低。當(dāng)選取不同抗蛇行減振器節(jié)點(diǎn)剛度時(shí)，前后轉(zhuǎn)向架橫移、側(cè)滾、搖頭加速度功率譜密度變化相對(duì)于節(jié)點(diǎn)剛度取值非常敏感。因此，在不同頻率范圍內(nèi)，合理選擇抗蛇行減振器橡膠節(jié)點(diǎn)剛度有利于減小轉(zhuǎn)向架功率譜密度，能夠有效提高轉(zhuǎn)向架橫向運(yùn)動(dòng)的平穩(wěn)性。