高速列車車體小部件模態修正及試驗驗證

張海進，趙艷菊，郭建強，帥仁忠

(中車青島四方機車車輛股份有限公司，山東 青島 266111)

目前高速列車車體大多采用輕量化的鋁合金材料，使得車體的固有頻率降低。列車在高速運行過程中車體不僅受到來自輪軌的寬頻振動激勵，還受到較大的氣動載荷壓力，使車體產生了較大的振動能量[1-2]。因此研究車體的振動特性對提高乘客的乘坐舒適性有著重要的意義，也為設計與優化高速列車車體提供理論基礎[3-4]。有限元分析是高速列車車體設計中的重要方法，但由于初始的簡化假設、邊界模擬的差異以及非結構構件等因素的影響，使得建立的有限元模型總與實際模型存在差異，造成計算值和試驗測量值存在一定偏差。結構有限元模型的修正是以試驗模態的結果參數為目標，在一定范圍內對有限元模型參數(如幾何參數、約束邊界、材料屬性等)進行修正，使結構的動力特性的理論值更趨于實測值[5-6]。高速列車特殊的雙層薄壁型材結構導致有限元網格多，計算量大，需要在保證精度的前提下提高計算效率。張德文 等對模型修正的理論與方法進行了詳細的闡述[7]；費慶國 等通過數值算例對以模態參數為特征量的有限元模型修正技術進行了深入探討[8]；Kenigsbuch et al.選取模態頻率和模態振型作為特征量對6自由度的彈簧質量體系進行了修正[9]；Mottershead和Friswell在利用模態參數進行模型修正方面作了大量的研究，分別研究了基于模態頻率、模態頻率+模態振型、模態頻率+模態置信度的修正方法[10-11]。

初始有限元建模是有限元模型修正的出發點，該模型提供了修正的初值，應以盡可能小的誤差反映結構的真實特性。良好的初始有限元模型對于修正的速度、精度乃至修正的成敗至關重要。初始有限元模型的誤差分為結構誤差、參數誤差和階次誤差三類[12]。結構誤差可以通過尋找合理的數學模型解決，階次誤差也可以通過有限元網格離散疏密得到最大限度的縮小。因而有限元模型修正的焦點是怎樣縮小有限元模型和實際結構之間的參數誤差[13]。

本文以高速列車車體型材為對象，對其進行有限元建模、模態計算，同時對其進行試驗模態分析，將有限元計算結果和試驗結果進行對比，利用基于靈敏度分析的有限元模型修正方法[14-15]，對型材的有限元模型進行修正并進行模態計算。

1 基于靈敏度分析的有限元模型修正

基于靈敏度分析的參數型模型修正方法的實現是一個迭代的過程，主要包括以下步驟：初始有限元建模、有限元分析、試驗建模及分析、試驗振型擴充/有限元模型縮聚、相關分析、誤差定位/參數選擇、靈敏度及殘差分析、修正量求解、收斂判斷、質量檢驗等。已知結構的有限元模型共有n個設計參數，其中前m個為待修正的參數，則設計參數p可以表示為：

(1)

結構的總體剛度陣K和質量陣M可以用設計參數p的函數表達：

(2)

則對應的特征量可以表示為設計參數的函數：

f=F(K,M)=F(fK(p),fM(p))=fp(p)

(3)

式(3)中，f可以是任意的特征量，如模態頻率、模態振型等，或者是它們之間的組合。模型修正問題轉化為如下的優化問題：

(4)

式中：fe，fp(p)——分別為結構動態特性的試驗值與分析值；

該公司的科學家通過“關閉”大豆中反式脂肪酸基因研發出這一款轉基因大豆。與傳統的大豆相比，這種大豆榨取的豆油含有更多“健康”的脂肪酸，而導致人體膽固醇增多的脂肪酸更少。

R(p)——殘差項；

VLB，VUB——分別為結構設計參數變化的上下限；

Wf——結構各個特征量之間的加權矩陣。

通常情況下，fp(p)為設計參數的非線性函數。為將非線性問題轉化為線性問題，在初始設計點將fp(p)展開成待修正參數的一階泰勒表達式：

fp(p)=fp(p0)+SΔp

(5)

其中：

(6)

式中：S——特征量對設計參數的靈敏度矩陣；

p0——設計參數初始值；

Δp——設計參數的誤差，Δp=p-p0。

WfSΔp=Wf(fe-fp(p0))

(7)

式(7)就是常見的模型修正方程，且是一個迭代優化的過程。

2 型材有限元模態計算和試驗模態測試

2.1 型材有限元模型仿真計算

本文中使用1.5 m×1.2 m的高速列車車體用鋁型材進行建模仿真計算及試驗模態測試，型材實際質量為35 kg，材料密度取2 800 kg/m3，確保模型總質量為35.04 kg。型材及幾何模型如圖1所示。為了比較網格尺寸對模態分析結果的影響，精細模型的網格為30×20，粗糙模型網格為20×10(圖2)。

圖1 型材及幾何模型

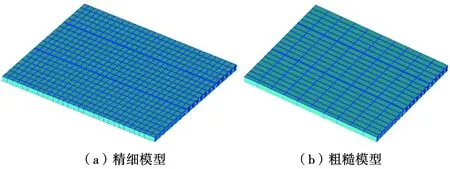
圖2 2種有限元模型(FEM)

對2種有限元模型進行模態計算，得到的前14階模態頻率見表1。從表1中可以看出，隨著階次頻率的增加，有限元精細模型和粗糙模型的計算結果偏差越來越大。圖3～圖6為2種有限元模型計算的前4階模態振型。

表1 FEM精細模型和粗糙模型模態計算結果

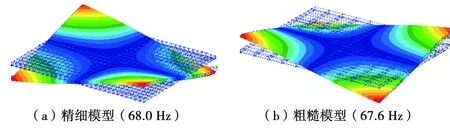
圖3 1階扭轉振型

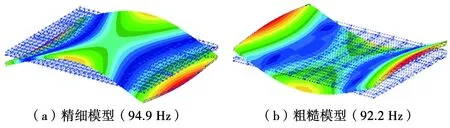
圖4 1階縱彎振型(1.5 m方向)

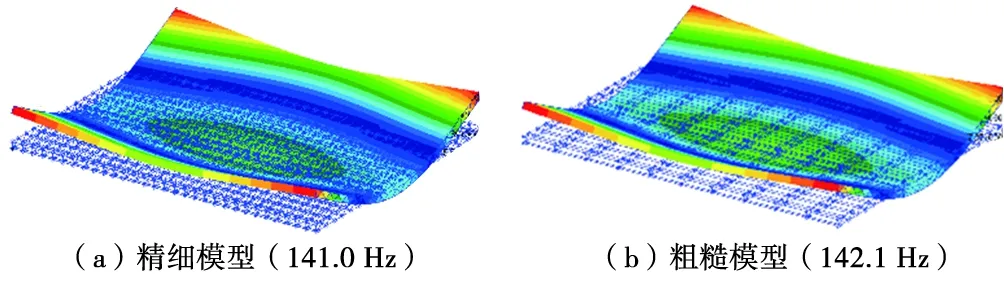
圖 5 1階橫彎振型(1 m方向)

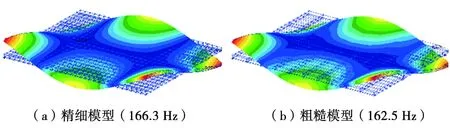
圖 6 2階扭轉振型

2.2 試驗模態測試

試驗模態中橫向和縱向各布置11個測點，整個型材共布置11×11個測點，采用移動錘擊法進行模態試驗測試，頻率測試結果見表2，前4階模態振型如圖7所示。

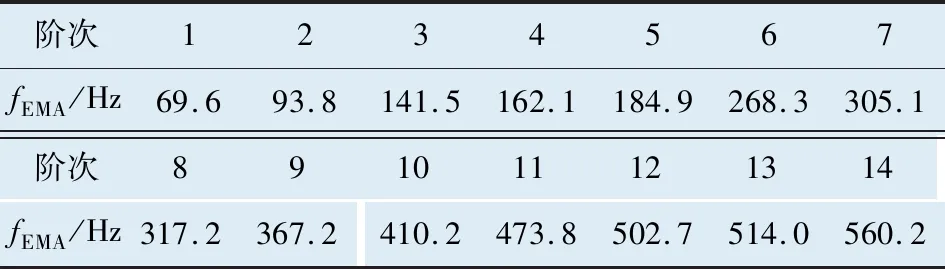
表2 試驗模態(EMA)測試結果

圖7 試驗模態振型

2.3 相關性分析

根據有限元模型修正的定義可以看出，無論哪一種修正方法，都是某種類型的有限元分析結果與試驗結果根據某種準則進行比較的結果，因此，模型修正技術首要考慮的就是理論-試驗模型的相關性分析。相關性分析的作用是為了確定計算分析結果和試驗測試結果的對應關系和誤差準則，以便進行模態匹配。模態匹配的方式除了對振型進行比較、觀察外，還可以利用數值的手段，例如模態比例因子(Modal Scale Factor,MSF)和模態置信度(Modal Assurance Criterion，MAC)。

模態置信度，也稱為振型相關系數，是一個介于0～1之間的標量，如2個振型向量的MAC值為1，則說明2個振型向量代表的是同一階模態，為0則代表不同模態[16]。實際運用時，MAC是一個矩陣，好的相關性要求MAC矩陣的對角元>70%，非對角元<10%。對2種有限元模型和試驗模態進行振型相關性分析，選擇z向平動自由度進行MAC計算，結果見表3，前14階MAC值三維柱狀圖如圖8所示。

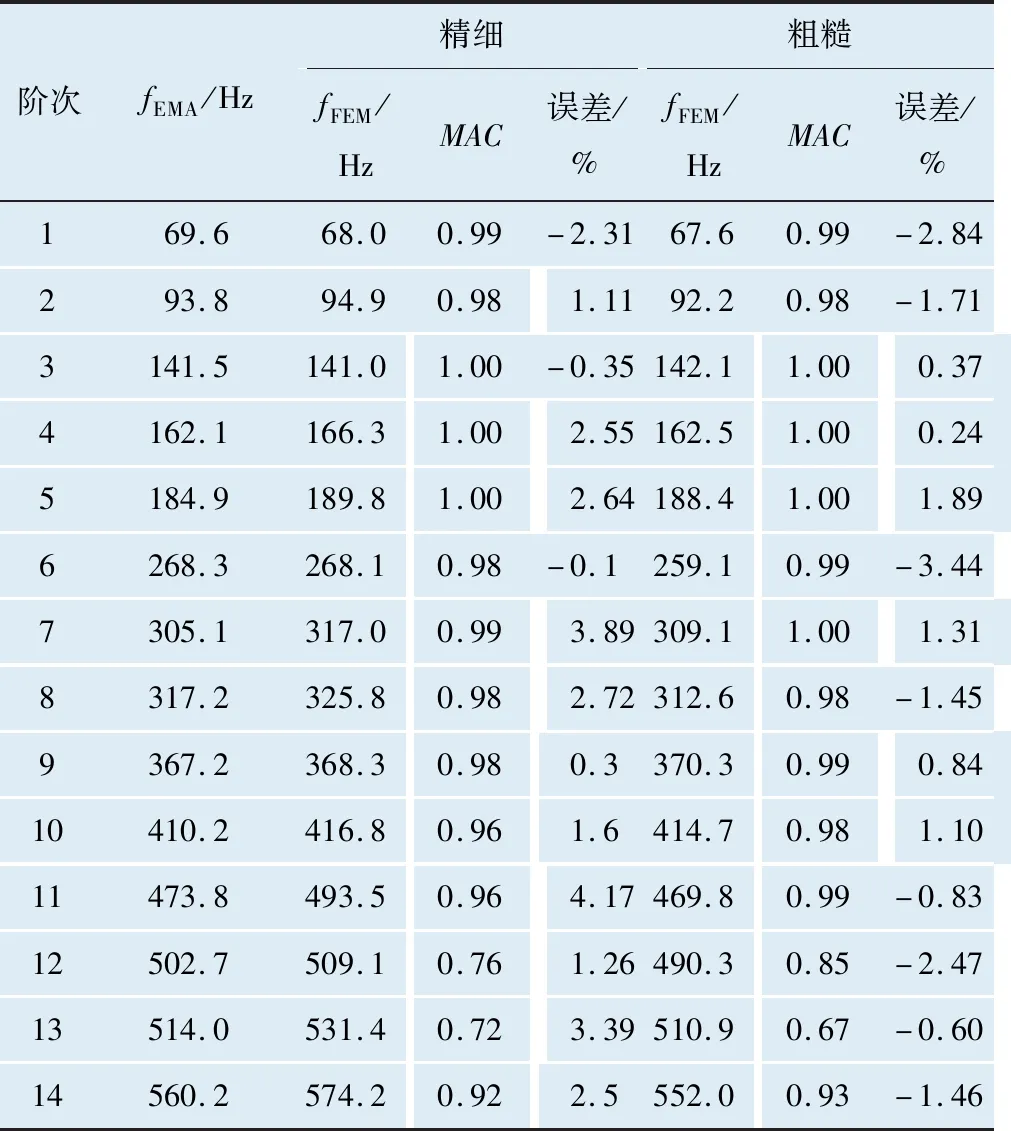
表3 有限元計算模態與試驗模態匹配結果

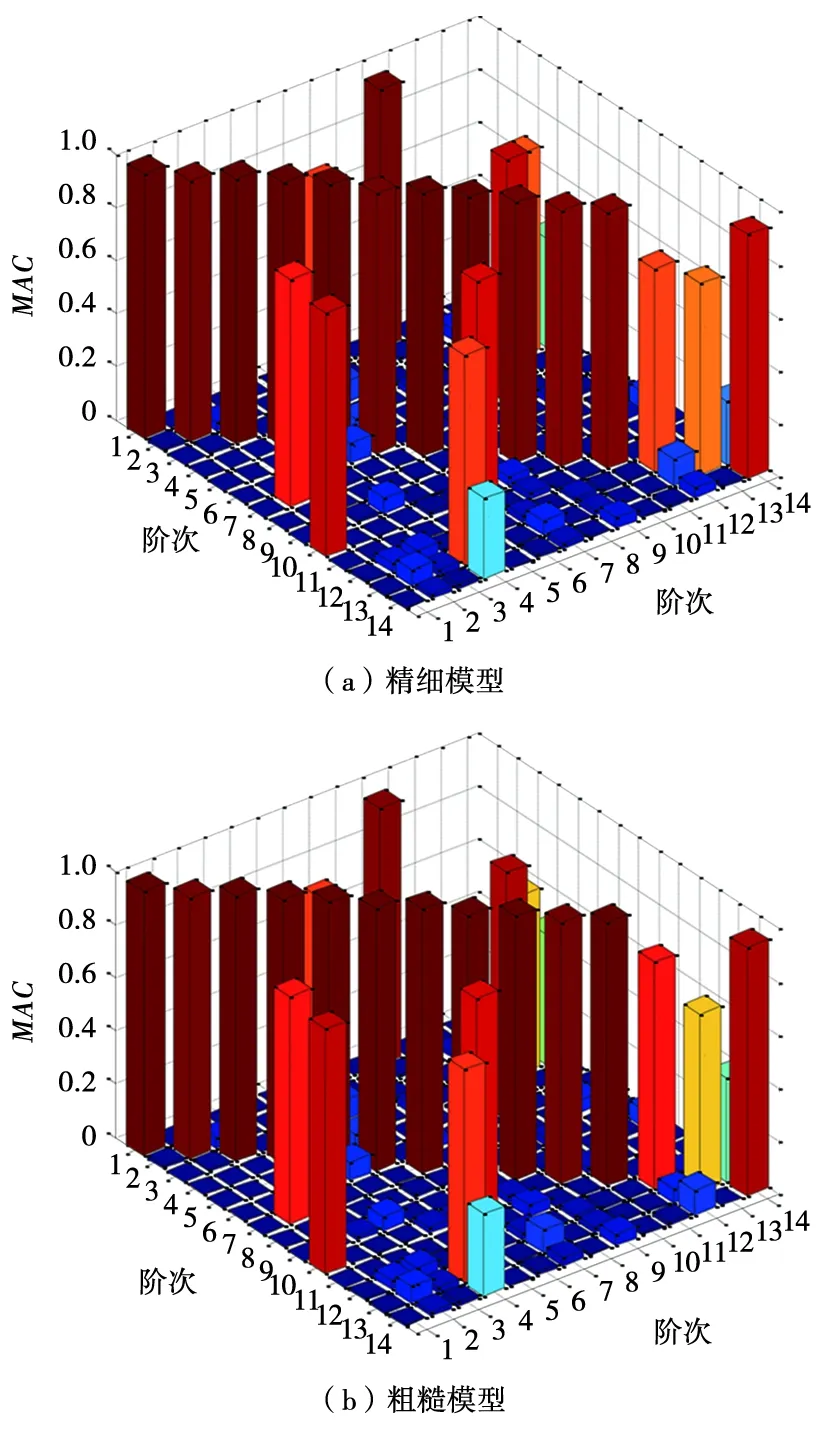
圖8 有限元計算振型與試驗振型MAC值匹配三維柱狀圖

在型材的前14階模態中，有限元計算結果和模態試驗結果的MAC值都比較高，頻率誤差都在5%以內。通過2種有限元模型計算結果和試驗結果的比較可知，粗糙模型的模態頻率誤差更小，主要原因是粗糙模型在1.5 m方向的單元數量與試驗測點數一致，與試驗結果更加接近；采用長條形的粗糙模型并沒有降低模態計算的精度，因此在大型型材有限元建模中，完全可以采用該方法降低模型單元數量，從而減小計算量。

3 有限元模型修正

在模型修正中，當特征量選取模態頻率、模態頻率+MAC值、模態頻率+振型來對有限元模型進行修正時，如果要求修正以后的有限元模型能夠充分、完整地復現試驗數據，而且能夠保證修正后的各階振型保持正交，角度盡可能的大，那么特征量選擇模態頻率+MAC值修正的效果最好[12]。為了便于模型修正，將初始有限元模型進行修改，建立預修正模型。將型材的上下兩層和中間層、焊縫層以及直筋分別采用不同的材料進行描述，將5個材料的彈性模量作為待修正參數，選擇前14階頻率及對應的MAC值作為修正目標，采用QP優化方法進行迭代。E1～E5表示型材5種材料的彈性模量，為5個待修正參數，迭代修正結果如圖9所示。從圖9中可知，各參數迭代大約25步后基本收斂。

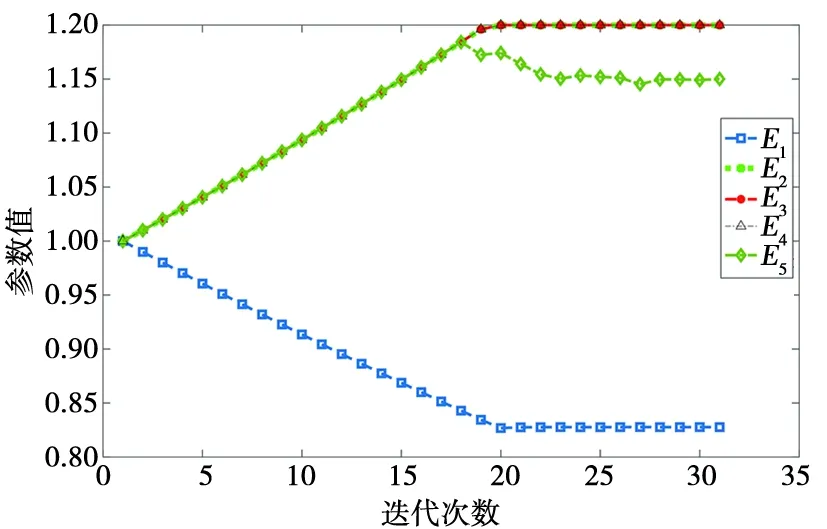
圖9 參數修正迭代收斂圖

同樣對前14階目標頻率殘差采用QP優化方法進行迭代修正，結果如圖10所示。從圖10中可以看出，各階頻率殘差在迭代20步以后基本趨于收斂，誤差最大的為第1階模態頻率殘差，收斂后最大誤差為-3.2%左右。各階修正目標MAC值迭代結果如圖11所示。從圖11中可以看出，迭代修正過程中，除12階MAC值略有降低外，其他各階MAC值均有明顯提高。

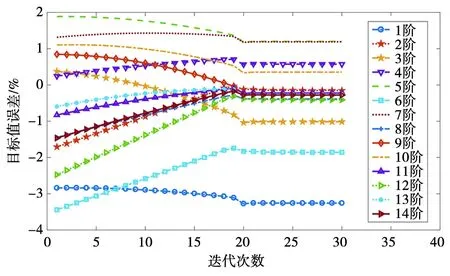
圖10 各階模態頻率收斂情況

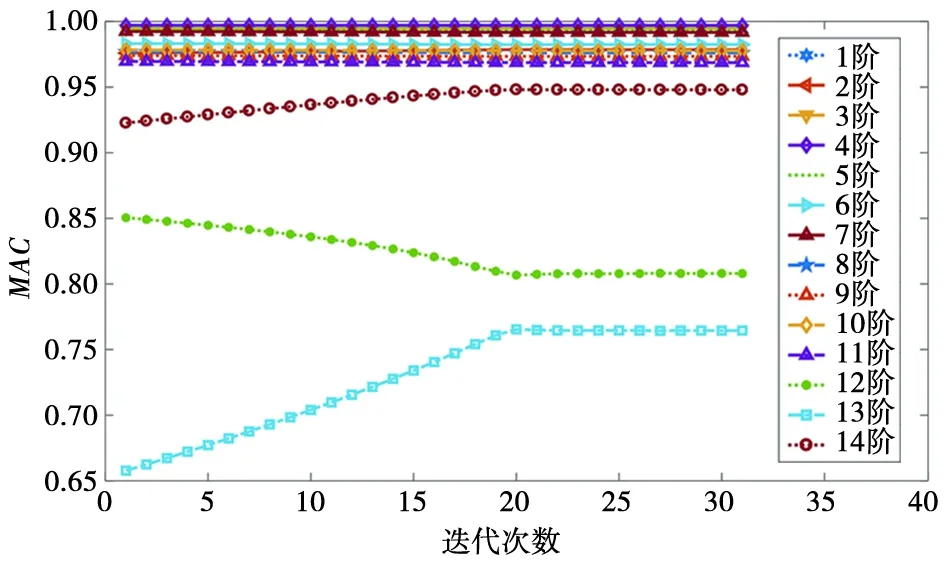
圖11 各階MAC值收斂情況

將有限元粗糙模型修正前后的MAC值與頻率誤差比較結果列于表4中。從比較結果可知，有限元模型頻率初始誤差最大為-3.44%，絕對平均誤差為1.47%，修正后最大為-3.23%，絕對平均誤差為0.82%；MAC值基本都有所提高，均值從修正前的0.95提高到修正后的0.96。

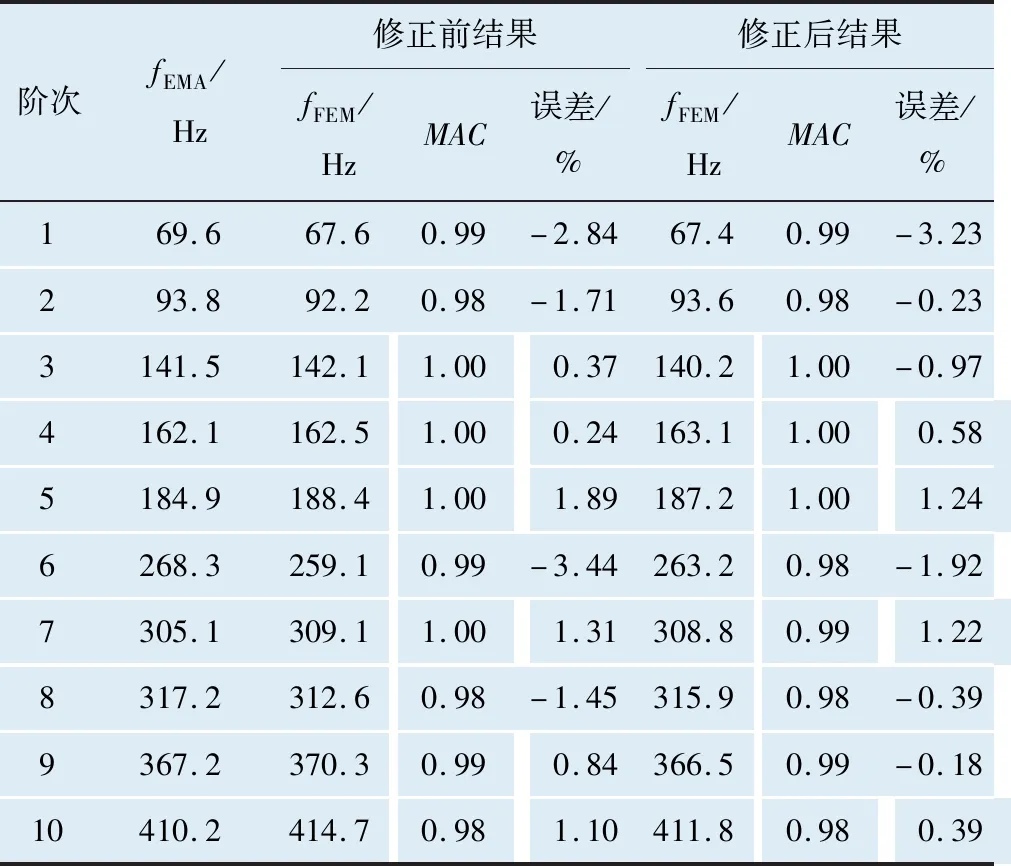
表4 粗糙模型修正前后有限元計算模態與試驗模態匹配結果

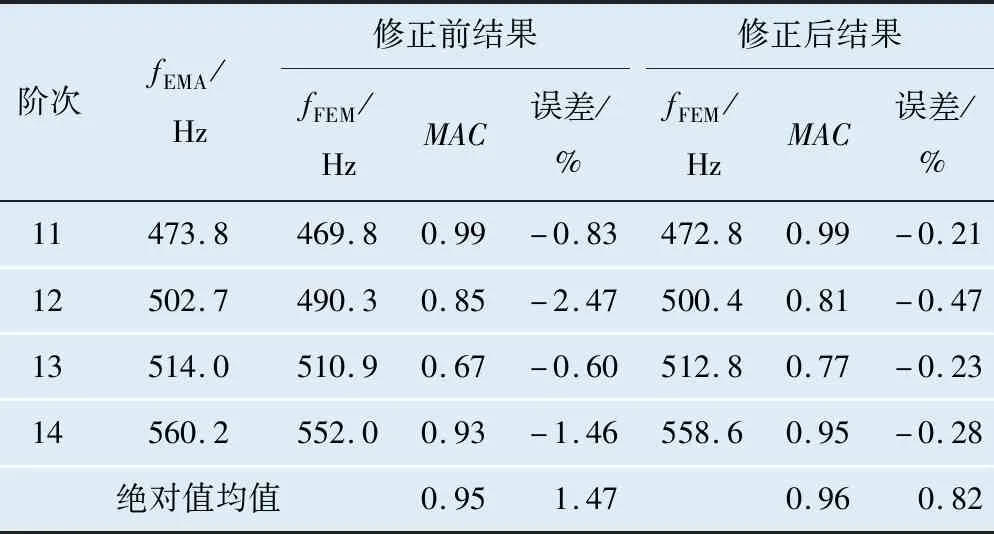
續表4

4 結論

(1) 本文對高速列車車體型材進行了2種不同的有限元模態計算，并對車體型材進行了試驗模態測試。將2種有限元模態計算結果與試驗模態測試結果進行了對比，由于粗糙模型在1.5 m方向的單元數量與試驗測點數一致，所以粗糙模型計算的模態頻率與試驗模態測試結果更接近。

(2) 采用長條形單元的粗糙模型進行有限元模態計算并沒有降低模態計算的精度，因此對于高速列車車體等大型結構進行有限元網格劃分時，可以采用較為粗糙的單元來降低有限元模態分析計算量。

(3) 利用基于靈敏度分析的有限元模型修正方法對模型進行修正之后，得到了更高精度的等效有限元模型。模型修正后，前14階的頻率絕對平均誤差均值由1.47%降到0.82%，MAC均值由0.95提高到0.96。可見，經過修正之后得到了更為準確的有限元模型。