獨塔斜拉-T構協作體系橋梁靜風穩定性研究

張友忠 宋重陽

(1.廣東省路橋建設發展有限公司 廣州 510000; 2.中交第二公路勘察設計研究院有限公司 武漢 430074)

大跨度纜索橋梁由于橫向剛度較小，在靜風荷載作用下，主梁會發生較大的橫向彎曲及扭轉變形，當橋梁附近風速達到靜風失穩臨界風速時，主梁的豎向、橫向，以及扭轉位移顯著增大，從而導致橋梁在靜風荷載下失穩[1]。隨著橋梁跨徑逐漸增大，橋梁組合體系的增多，橋梁的剛度逐漸降低，而纜索橋梁的靜風失穩正在成為制約纜索橋梁向大跨徑方向進一步發展的主要原因。

橋梁靜風失穩問題最早由Hirai[2]在懸索橋風洞實驗時發現，結構在靜風荷載作用下發生了靜力扭轉發散的現象，之后同濟大學學者也同樣發現了類似情況的發生[3]。學者們意識到風荷載不僅會導致橋梁振動失穩，同樣會導致橋梁靜力失穩。雖然目前纜索橋梁的三維非線性靜風失穩理論和實驗方法已經廣泛運用于大型橋梁中[4-6]，但是特殊地形導致的特異風場同樣使得纜索橋梁的靜風失穩成為關注的熱點。張文明等[7]研究了特征紊流抖振力對大跨度橋梁靜風穩定性的作用。胡朋[8]研究了山區峽谷非均勻特異風場對大跨度橋梁靜風穩定性的影響。除了上述研究方向，不少研究者擬揭露大跨徑纜索橋梁的靜風失穩機理，胡傳新等[9-10]基于風洞實驗根據結構剛度的變化過程揭示了大跨徑三塔斜拉橋靜風失穩機理。郝憲武[11]同樣分析出大跨非對稱懸索橋由于主梁扭轉變形和纜索的豎向位移隨著風攻角的增大而增大，重力剛度大幅降低是導致橋梁靜風失穩的原因。

盡管目前已對兩塔和三塔斜拉橋的靜風失穩研究較為深入，但是還沒有對獨塔斜拉與T構協作體系橋梁的靜風失穩進行研究。因此，本文以金馬大橋為研究對象，基于FLUENT建立數值風洞模擬求解出主梁斷面隨風攻角變化的三分力系數，并基于ANSYS建立三維有限元模型，考慮結構幾何非線性和靜風荷載非線性,通過內外兩重迭代相結合判別靜風失穩的臨界風速。擬從結構位移變化過程揭示獨塔斜拉與T構協作體系橋梁靜風失穩內在機理。

1 工程概況

1.1 結構體系

金馬大橋是位于廣肇高速公路上的一座主跨為283 m的協作體系組合橋梁。主橋由一座2×223 m獨塔斜拉橋與2座2×60 m的T構組成。斜拉部分主梁截面采用雙邊主梁形式，梁高為2 m，橫隔和斜拉索的間距分布為4 m和8 m。有限元模型示意見圖1。

圖1 金馬大橋有限元模型

1.2 動力特性

利用ANSYS建立全橋空間有限元模型。主梁采用雙主梁模型，主梁節點設置在拉索下錨點處，兩根梁之間通過真實橫梁進行連接。其中主梁和橋塔采用beam188單元，斜拉索采用給定初應變的link10桿單元模擬，分別用shell63和mass21單元模擬承臺和二期恒載。樁基底部的邊界條件為固結，T構左右兩側均釋放縱橋向約束，同時根據土質計算等效剛度彈簧從而模擬樁基礎周邊的土效應。金馬大橋前10階自振頻率表見表1，其中一階豎彎和一階扭轉振型圖見圖2和圖3。

表1 自振頻率

圖2 一階豎彎振型圖

圖3 一階扭轉振型圖

2 三維非線性靜風失穩分析

2.1 有效風攻角

根據受力的風向，主梁在橫向靜風荷載作用的受力可分為：橫向風荷載FH，豎向風荷載FV和扭轉力矩M。由于靜風作用會導致結構發生變形，因此盡管靜風自身保持不變，但風向與主梁截面間的相對風攻角會隨著結構狀態發生改變，因此通過引入靜力三分力系數來考慮有效風攻角變化的影響。靜風荷載具體表達式如下。

(1)

式中：ρ為空氣密度；D為主梁側向投影的高度；B為主梁寬度；U為平均風速；CH(α)、CV(α)、CM(α)為通過數值風洞或真實風洞得到的靜力三分力系數；α為有效風攻角，取靜風初攻角與主梁截面扭轉產生的轉角之和。

2.2 分析過程

纜索承重橋梁在靜風作用下不僅存在靜風荷載的非線性，其自身的幾何非線性也不可忽視。為了準確、全面地考慮雙重非線性因素對橋梁的影響，需要對結構在風速增加的全過程中的位移響應進行分析，從而準確預測出結構靜風失穩臨界風速。采用第二類穩定理論對這類橋梁的空氣靜力穩定問題進行求解。

{[TK0]}+[TKσ]{Δδ}={T+ΔTF{α}}-{TR}

(2)

由于靜風荷載有效風攻角和結構變形間的耦合作用，在對式(2)進行求解時，首先須將風速逐步增加，從而計算在各級風速下的結構響應。而在逐級增加風速的同時還需修正有效風攻角。而主梁每節點的位移響應不同導致有效風攻角均會不同，最終導致施加在主梁節點的靜風荷載也有區別，因此計算結構臨界失穩風速的前提是必須有效地控制靜風荷載三分力系數的歐幾里得范數，其全過程計算步驟如下。

1) 確定結構在恒載狀態下的幾何構型和初始內力。

2) 設定初始風速V0。

3) 根據初始風速和初始風攻角確定靜風三分力荷載。

4) 通過ANSYS，采用其中的Newton Raphson迭代法求解式(2)，記錄在當前風速下主梁所產生相應的位移。

5) 根據結構位移計算主梁扭轉角，更新有效風攻角并重新計算相應的靜風荷載。

6) 根據式(3)檢算主梁靜風荷載三分力系數的歐幾里得范數

(3)

式中：Na為主梁的節點數；Ck為阻力、升力和升力矩系數；εk為容許的收斂值。

7) 當滿足式(3)的收斂準則時，增加靜風荷載，并重復步驟3)～5)；否則，重復步驟4)、5)，修正有效風攻角，直至歐幾里得范數滿足要求。

8) 當結構位移增量較大時，三分力系數的歐幾里得范數難以收斂，風速增量步長適當減小，直到結構失穩，從而得到結構的臨界失穩風速。

9) 輸出結果。

3 三分力系數計算

考慮橋梁欄桿對三分力系數計算的影響，其在有限元軟件模擬所采用的斷面圖見圖4。采用ANSYS Fluent建立2D流場，為了保證計算準確性，流場左側入口距橋梁斷面10倍橋寬，流場右側出口距橋梁斷面20倍橋寬，流場上下距橋梁斷面10倍橋寬。采用SSTk-ω湍流模型，方程求解采用SIMPLE算法。為提高計算效率，橋梁斷面縮尺20倍。模型流場采用結構化網格，主梁斷面位置為非結構化網格。流場左側邊界設置為invelocity，流場左側邊界設置為outpressure，流場上下側邊界設置為symmetry，主梁斷面邊界設置為wall。

圖4 金馬大橋主梁斷面圖(單位：cm)

FD、FL和M分別表示以風軸系為參考，主梁所承受的靜風阻力、靜風升力和靜風力矩；FH、FV和M′分別表示以體軸系為參考，主梁所承受的靜風阻力、靜風升力和靜風力矩；ρ表示空氣質量密度，取ρ=1.225 kg/m3；α為來流攻角。靜力三分力的作用方向見圖5。

圖5 三分力方向示意圖

主梁體軸系三分力與風軸系三分力之間的轉換如式(4)所示。

(4)

通過數值模擬得到從-7°到7°風攻角步長為2°的三分力，并通過式(1)和式(4)計算了體軸下的三分力系數，結果見圖6和表2。通過分析結果可知，金馬大橋主梁截面在0°風攻角為時，阻力系數最小。隨著正負風攻角的絕對值增大，導致主梁迎風面的增加使得其阻力系數和升力系數逐漸增大，而扭矩系數對風攻角的變化并不敏感。

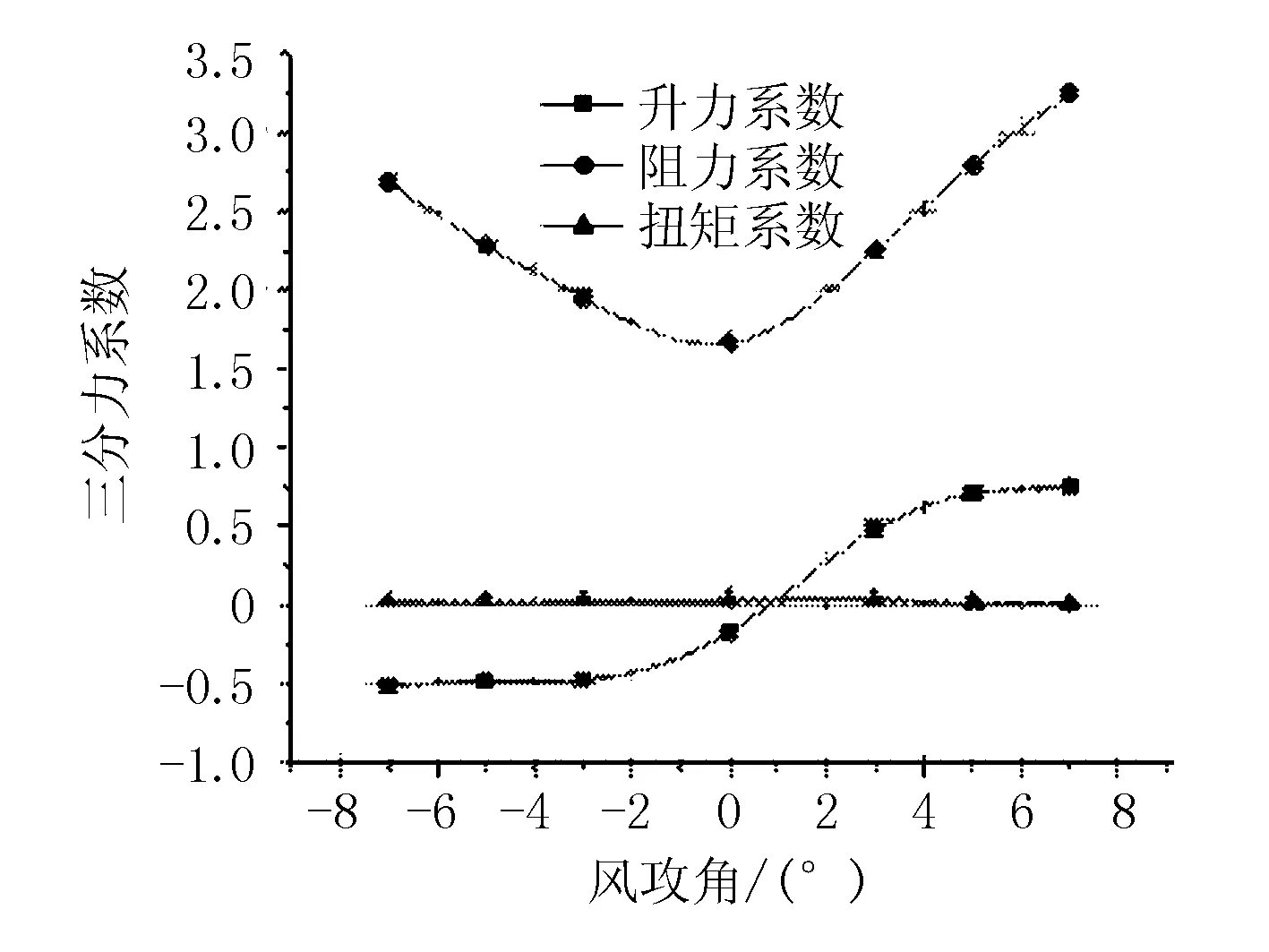
圖6 成橋狀態主梁斷面三分力系數

表2 成橋狀態主梁斷面三分力系數

4 三維非線性靜風失穩分析

4.1 數值模擬結果

規范對橋梁進行三維靜風穩定性分析時，驗算的風攻角主要考慮0°、±3° 3種荷載工況。將結構的成橋狀態作為分析模型的初始狀態，通過設置風速增量從而逐漸增大風速，并依次記錄下各級風速下主梁的豎向、側向和扭轉位移。

金馬大橋主梁在0°和±3°風攻角作用下，跨中橫向、豎向及扭轉位移隨風速變化的規律見圖7、圖8。

圖7 成橋狀態主梁最大位移

圖8 成橋狀態主梁最大扭轉角

當風速較低時，主梁各方向位移的變化速率均較小。當風速超過一定限值時，主梁的側向位移逐漸增大，且速率逐漸增大，而豎向和扭轉位移的增量則相對較小；當風攻角為-3°時，主梁的最大橫向位移一直略大于風攻角為0°和3°計算得到的結果。當風攻角為0°和3°時，主梁的最大豎向位移隨著風速增大而逐漸向上增大，而風攻角為-3°時會導致主梁的最大豎向位移向下遞增。圖6表明，在風速低于250 m/s時，3種風攻角情況下的主梁最大扭轉角較為接近，當風速高于250 m/s時，主梁的最大扭轉角在風攻角-3°時的增加速率遠遠高于風攻角0°和3°。當風速增大到500 m/s以后，豎向位移和扭轉位移增量開始加速上升，當風攻角為-3°時，風速增大到800 m/s，當風攻角為0°時，風速增大到806 m/s，當風攻角為3°時，風速增大到812 m/s，計算程序因難以收斂而退出。這表明豎向、橫向和扭轉位移出現發散，結構已經在對應靜風力作用下喪失穩定性，此時結構側向位移也有發散的趨勢。

4.2 失穩機理

通過分析計算可知，在初始風攻角為-3°，橋梁整體靜風失穩時主梁的最大扭轉角達到1°。在風攻角為0°和3°時，在結構臨近失穩時主梁的扭轉角分別為0.45°和0.37°。可以發現風速增大對橋梁的扭轉角的影響較小，其原因主要為風攻角的改變對主梁斷面的扭矩系數幾乎沒有影響，同時由于獨塔斜拉橋兩側T構和斜拉橋的空間索面均對主梁的扭轉有一定的約束作用，因此直至橋梁整體失穩，主梁也沒有發生較大的扭轉。在初始風攻角為-3°，在結構臨近失穩時主梁的豎向位移達到了-1.11 m，而在初始風攻角為0°和3°時，直至結構靜風失穩，整體結構的最大豎向位移也未超過0.3 m。其主要原因為獨塔斜拉橋和T構均為混凝土主梁，其恒載能夠有效抵抗靜風的豎向分力。在初始風攻角為-3°，0°和3°時，主梁的最大橫向位移達到了2.79，2.58和2.50 m。

通過前面分析該組合橋梁的靜風位移發展，總結該橋的失穩過程為: 隨著風速不斷增長，附加風攻角隨著主梁扭轉角的增長而增長，導致有效風攻角也隨著附加風攻角的增大，從而使得主梁的橫向位移不斷增大，最終導致橋梁發生整體靜風失穩。影響橋梁結構失穩臨界風速最大的是主梁上的靜風阻力荷載作用，靜風升力次之，靜風力矩作用影響最小，所以由此可以看出影響獨塔斜拉-T構協作體系橋梁靜風穩定性的主要因素是主梁上的靜風阻力作用。

5 總結

1) 風攻角的改變對雙邊主梁的扭矩系數影響較小。因此當采用雙邊主梁作為斜拉橋主梁時能夠有效防止在風攻角較大時主梁產生較大力矩。

2) 獨塔斜拉與T構協作體系橋梁的靜風失穩形態是以主梁發生橫彎和豎向位移為主，同時也有一定扭轉的三維對稱彎扭耦合變形狀態。由于獨塔斜拉橋主梁受到空間索和T構的約束作用，靜風失穩主要體現為由于主梁橫向位移過大導致的結構整體失穩。